基于组合预测模型的社会矛盾件数变化动态监测研究
——以人民调解为例
张文德 刘 静 倪必勇
(1. 福州大学信息管理研究所, 福建福州 350108;2. 中共福建省委政法委员会, 福建福州 350003)
一、引言
社会矛盾的日益多元化对社会治理提出了新的要求,先进信息技术和手段为发现矛盾件数变化的未来趋势走向提供了可能性,通过预测出的趋势变化提前采取相应的措施能够提高社会矛盾治理的精确性和有效性,因此,实现社会矛盾件数变化的动态监测迫在眉睫。我国学者研究社会矛盾主要集中在社会矛盾的内涵和突出事件两个方面。部分学者对社会矛盾风险进行了动态研究,例如:陆益龙基于对民众纠纷的调查构建了社会风险监测指标体系,得到群众倾向的解决纠纷方式,但此种方法主观因素太强,缺乏客观性。[1]林小叶设计的社会矛盾纠纷动态评估体系实现了宏观层面的矛盾纠纷管理,但纠纷种类的多样性使得该体系不能得到实际应用。[2]查庆九等描述了雅安市司法局社会矛盾纠纷动态管理评估机制的调研现状,在宏观层面上形成了比较整体的纠纷动态管理方法。[3]但是社会矛盾的治理关键在于基层,形成微观层面的社会矛盾治理方法极为重要。经过实地调研我国某省司法厅的人民调解工作以及该省各地市、区县的矛盾纠纷治理现状,发现矛盾纠纷多元化解工作在实际运行中存在着许多不足:一是现实中各部门缺乏对矛盾件数的智能预测功能,即尚未实现动态监测;二是社会矛盾治理的各个政府部门间的数据壁垒尚未打破,由于掌握的数据量较少,单个部门很难利用已有数据去挖掘深层规律。
人民调解工作是我国社会矛盾治理的重要环节,是维护基层社会稳定的“第一道防线”,做好人民调解工作能够有效提高社会矛盾治理的效率。人民调解的关键在于排查化解,意在预防矛盾纠纷演变成突出事件。一直以来,人民调解的排查工作都是在矛盾纠纷产生后进行调解,调解员处于被动化解状态,尚未实现动态监测某社区、某城镇乃至某市区矛盾件数的功能。我国学者关于人民调解的研究大多集中于机制,例如:毋爱斌、殷向杰和梁平分别从不同视角构建了多元治理机制[4][5][6],陶林提出了建立社会矛盾预警和应急机制的具体建议[7],但是尚未对人民调解进行动态监测研究。部分学者研究了矛盾件数的预测模型,常见的是灰色预测模型,例如:陈凌等、张云河等和陈天学等分别将灰色GM预测模型代入纠纷数据进行了运算[8][9][10],Yao T也阐述了GM(1,1)模型的适用范围。[11]这些模型在理论上能够得到预测数值,但由于研究对象受许多相关因素持续影响,如人民调解工作涵盖了包括调解组织、调解人员和矛盾件数(如图1所示),仅通过研究对象的数据来预测缺乏现实意义。因此,我国学者提出了各种组合预测模型,例如:曾波等构建了基于关联度和GM(1,1)模型的灰色组合模型[12],但验证该模型时选择的目标序列与相关序列是已知的,不符合人民调解工作;而郭婧英利用灰色关联度构建由模拟数值和真实数据组成的新目标序列[13],也不能解决人民调解工作干扰因素多的问题。由于Tien指出GM(1,N)模型单独应用于实验得到结果[14]是不准确的,而利用灰色综合关联度方法得到的关联度较为稳定,不会因为选择的数据段不同而改变,本文将建立基于灰色综合关联度和GM(1,N)模型的组合预测模型,并预测全国人民调解矛盾件数的变化趋势,从而实现对人民调解矛盾件数的动态监测,完善社会矛盾治理的内涵,为政府部门提供决策依据,提高社会矛盾治理的科学性和有效性。

图1 人民调解工作扁平化结构
二、组合预测模型
灰色关联分析是利用序列曲线的近似度来判断序列间的联系,关联度越大的序列曲线的趋势越相似。[15]在对目标序列进行预测时,由于不能及时获得目标序列的最新数据,仅根据目标序列已有数据进行预测往往不够精确,缺乏现实意义。现实业务中,各政府部门在收集目标序列数据的同时往往也会收集相关因素序列的数据,这些数据的时间节点可能更新,借助于这些最新的相关因素序列数据能够辅助目标序列数值变化趋势的预测,增添可操作性和现实意义。因此,本文构建了基于这一情形的组合预测模型,通过计算人民调解矛盾件数相关因素的灰色综合关联度并筛选出强关联因素,建立由矛盾件数和强相关序列组成的GM(1,N)模型,以此动态监测人民调解矛盾件数的趋势动向(建模流程如图2所示)。

图2 组合预测模型的建模流程
三、运算过程


步骤二:分别计算X0与Xi的灰色绝对关联度ε0i和灰色相对关联度r0i,其中,
步骤三:计算X0与Xi的灰色综合关联度ρ0i,其中,ρ0i=θε0i+(1-θ)r0i,一般取θ=0.5,对ρ01,ρ02,…,ρ0M的大小进行排序后,筛选出与目标序列X0强相关的几个序列(ρ0i∈[0.65,1]),记为Yi,i=1,2,…,N且N 步骤八:若模型不合格,则返回步骤四;若模型合格,则预测目标序列下一年数值,并得到目标序列的变化趋势。 本文运用组合预测模型来预测我国的人民调解矛盾件数。为了验证该模型的精度和现实意义,选取1999-2014年我国人民调解工作相关数据,分别采用组合预测模型和GM(1,1)模型对1999-2014年的数据进行模拟并比较其精度,最后对2015和2016年的人民调解矛盾件数进行预测,比较矛盾件数的预测趋势走向和实际趋势走向。 1. 模型计算 步骤一:从《中国统计年鉴》以及某省统计年鉴中选择了有关人民调解工作的数据,经整理后确定目标序列为全国人民调解矛盾件数序列X0(单位为万件),相关因素序列为:婚姻家庭矛盾件数序列X1(单位为万件),房屋、宅基地矛盾件数序列X2(单位为万件),邻里矛盾件数序列X3(单位为万件),损害赔偿矛盾件数序列X4(单位为万件),人民调解委员会个数序列X5(单位为万个),调解人员数量序列X6(单位为万人)和某省人民调解矛盾件数序列X7(单位为万件)。 表1 人民调解的目标序列与相关因素序列 (1)计算灰色综合关联度。 步骤二:计算上述序列的灰色绝对关联度ε0i和灰色相对关联度r0i,结果见表2。 表2 目标序列与相关因素序列的关联度一览 步骤三:取θ=0.5,计算上述序列的灰色综合关联度ρ0i,结果见表2。可知ρ07>ρ04>ρ03∈[0.65,1],即邻里矛盾件数序列X3,损害赔偿矛盾件数序列X4,某省人民调解矛盾件数序列X7为全国人民调解矛盾件数序列X0的强关联序列。 (2)计算GM(1,3)模型。随着时间的推移,系统内会产生新的干扰因素,这表现为最新数据相较于以往数据对系统有更强的影响力。因此,本文选择10年为此次建模的时间跨度,将2005年转化为序号1,2006年转化为序号2,依次类推,直至将2014年转化为序号10,最终形成新目标序列——全国人民调解矛盾件数序列Y0(单位为万件),新相关因素序列——邻里矛盾件数序列Y1(单位为万件),损害赔偿矛盾件数序列Y2(单位为万件)和某省人民调解矛盾件数序列Y3(单位为万件)。 表3 新目标序列和新相关因素序列的1-AGO 并计算参数列 7.66858117,10.35448128,12.93084033]T 步骤六:将参数列代入近似时间响应式,得到: 2. 模型验证 (1)计算10年为时间跨度的组合预测模型的原始数据和模拟值的残差与相对误差,结果见表4,可知平均相对误差为0.043446606<0.05,该模型的精度为二级。 表4 10年时间跨度下GM(1,3)模型误差检验 (2)若选择8年为此次建模的时间跨度,同理可得模拟值为: (3) 若选择5年为此次建模的时间跨度,同理可得模拟值为: 由于0.043446606<0.048834889<0.052221467,选择10年作为建模的时间跨度较为合适,该模型为: 3. 纠纷预测 已知2015年和2016年邻里矛盾件数为237.5和229.1万件,损害赔偿矛盾件数为73.1和75万件,某省人民调解矛盾件数为17.3和14.2万件,分别代入上述三种模型得到: 已知2015年和2016年全国人民调解矛盾件数的实际数据为933.1和901.9万件,则从表5可知三种模型中,仅10年时间跨度模型在两年的预测值呈现出了递减趋势。所以,选择10年时间跨度建模更贴近实际。 表5 三种时间跨度下GM(1,3)模型预测值 为方便比较,分别选择同等时间跨度的全国人民调解矛盾件数数据进行建模,结果如表6所示。 表6 三种时间跨度下GM(1,1)模型预测值误差 (1)若选择10年为此次建模的时间跨度(2005-2014),可得模拟值与原始数据的精度为三级,对2015年和2016年的预测值的平均精度为近68%;(2)若精度为三级,对2015年和2016年的预测值的平均精度为近72%;(3)若选择5年为此次建模的时间跨度,可得模拟值与原始数据的平均相对误差为0.011997738,精度为二级,对2015年和2016年的预测值的平均精度为近95%。 从表6可知,三种时间跨度模型中:选择10年时间跨度建模得到的平均相对误差为0.091435331,选择8年时间跨度建模得到的平均相对误差为0.09946197,选择5年时间跨度建模得到的平均相对误差为0.011997738。可知选择5年进行建模得到的模型精度最高,为二级,但三种时间跨度模型预测的未来两年变化趋势都为增加。所以,选择组合预测模型更适合,更符合现实趋势。 本文结合我国社会矛盾治理工作存在的实际困境——数据量少且杂并缺乏动态监测功能,提出了适合此种情形的基于灰色综合关联度和GM(1,N)预测模型的组合预测模型,并描述了建模流程以及运算过程,最后利用采集到的全国人民调解矛盾纠纷数据对该组合预测模型进行了验证,并与GM(1,1)模型进行了比较,发现利用组合预测模型方法得到的未来两年全国人民调解矛盾件数的变化趋势满足实际变化趋势。该模型所需数据量小,且得到的预测趋势符合实际情况,因此,可将该模型应用于社会矛盾治理实践中。例如,若是预测省级层面的矛盾件数,则相关序列是该省辖区内各个市的矛盾件数、该省各类别矛盾的件数、该省的调解人员总数和调解组织总数,通过预测到的矛盾件数变化趋势,对形成该趋势的几个强关联序列进行干预,采取制定与某种类别矛盾的相关政策、加强对个别市的调解人员或调解组织部署等方式,使该省未来的人民调解矛盾件数最终能实现下降趋势,真正实现源头治理、提高矛盾纠纷治理效率,从而提升矛盾纠纷治理的智能化建设水平,为社会治理提供新的治理思路。但该模型没有研究出更智能的数据时间跨度选择方法,未来将就此进行深入研究,以形成更完善的组合预测模型。 注释: [1] 陆益龙:《基层纠纷的社会风险及其动态监测》,《中共贵州省委党校学报》2017年第6期。 [2] 林小叶:《社会矛盾纠纷动态管理研究》,硕士学位论文,西南交通大学,2014年。 [3] 查庆九、张桂荣、张婧:《关于四川雅安社会矛盾纠纷动态管理评估机制的调研报告》,《中国司法》2013年第5期。 [4] 毋爱斌:《法院附设型人民调解及其运作——以“人民调解工作室”为中心的考察》,《当代法学》2012年第2期。 [5] 殷向杰:《医患纠纷协同治理研究》,博士学位论文,南开大学,2014年。 [6] 梁平:《多元化纠纷解决机制的制度构建——基于公众选择偏好的实证考察》,《当代法学》2011年第3期。 [7] 陶林:《社会治理创新视角下的基层社会矛盾预防和化解机制构建》,《公共管理与政策评论》2017年第4期。 [8] 陈凌、曹飞:《劳动争议案件数量的灰色预测及启示》,《技术经济》2007年第5期。 [9] 张云河、曹飞:《江苏劳动争议案件数量的灰色预测及启示》,《企业经济》2012年第12期。 [10] 陈天学、赵曼:《劳动法制约下劳动争议案件数量的预测方法》,《统计与决策》2014年第1期。 [11]YaoT.,LiuS.,XieN.,“OnthepropertiesofsmallsampleofGM(1,1)model”,Applied Mathematical Modelling,vol.33,no.4(2009),pp.1894-1903. [12] 曾波、刘思峰、方志耕:《组合预测模型及其应用》,《中国管理科学》2009年第5期。 [13] 郭婧英:《基于灰色关联度组合模型的能源消费预测研究》,《重庆理工大学学报》2017年第6期。 [14]TienT.L.,“AresearchonthegreypredictionmodelGM(1,n)”,Applied Mathematics & Computation,vol.218,no.9(2012),pp.4903-4916. [15] 刘思峰:《灰色系统理论及其应用》,北京:科学出版社,2010年。


四、应用实例
(一)组合预测模型
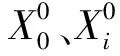









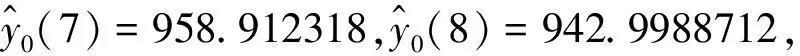








(二)GM(1,1)模型

五、结语
——黄胄画猫贺岁展

