户外广告资源配置优化模型及算法研究

朱 军，陈敬良，张安淇

（1. 上海理工大学 管理学院，上海 200093；2. 复旦大学 管理学院，上海 200433）

户外媒体是一种传统且行之有效的媒介形式，2017年我国户外广告总规模超过1 300亿元，较2016年度增长超过7%。据预测，随着新技术与新模式的应用，户外广告市场规模将进一步提升，在2021年户外广告的市场规模有望达到2 200亿元。户外媒体的选择与广告投放既是达到广告营销预期目标的保障措施，同时也是支付大量广告费用的商家最为关心的问题，并且是户外媒体运营商在企业战略、营销管理中的重要基础。

传统户外媒体运营者都是基于约定广告位置，按广告展示时间与广告位数量的双因素模式销售给广告主。从现有的户外广告媒体传播理论研究来看，对户外媒体的评估都是在空间生产理论的基础上，通过人工有限地进行数据采集，并结合经验进行评估，考虑了千人成本、人流量、可视机会等要素，但缺乏精准的大数据抓取，以及在此基础上的全面数据分析[1]。这不仅导致广告主的投放缺乏科学依据，也使媒体运营方受到广告时间及广告位数量限制，效益无法最大化。

户外广告媒体的建设由于需要占用有限的公共空间，投入大，回报周期长，不管是主管审批部门还是建设运营企业都需要对广告媒体进行更合理的规划，并基于精准的受众人群推送，衍生更多的营销形式，适应当下户外广告发展的需求。基于移动互联网技术的应用及其普及，户外媒体对受众大数据的获取及挖掘成为可能，进而实现对受众偏好的精准分析，并对户外媒体选择与广告效果评估方面产生根本性的影响[2]。随着全球定位系统（GPS）、无限局域网（WIFI）、蓝牙等传感技术的日益成熟，户外媒体已经可以精准收集其所在空间的用户数据，包括实时人流数量、空间距离、移动速度和方向等，并通过各类地理位置信息服务 （location based service，LBS）顺利地了解到用户的消费习惯、收入水平、关注领域等核心数据，勾画出准确的用户画像。此外，由于大数据基础建设在重点行业的日益完善，以及不同行业间底层支撑技术相同，广告行业在应用大数据时可以通过跨行业合作获得线上及线下数据[3]。

户外广告媒体价值的精准测算对广告运营公司而言具有重要的决策参考价值，广告运营公司可以通过户外广告资源的优化配置，更加科学有效地制定户外广告媒体的出售价格策略，从而更好地为公司盈利[4]。

本文结合户外广告的特点，基于LBS服务和大数据技术，提出户外广告资源配置优化模型，在满足广告主要求达到的广告营销预期目标的基础上，产生最大化的收益，突破传统双因素模式的局限性，通过数据分析方法研究户外媒体资源的优化配置策略，建立基于用户大数据的户外广告投放决策模型，为户外媒体的生产与价值提升提供了有效方法。

1 问题描述与模型建立

1.1 问题描述及符号表示

1.2 模型建立

户外媒体广告公司收益最大的数学模型为

其中：方程（1）是户外广告屏广告收入最大的目标函数，约束条件式（2）是指所有广告的支出不可以超过它的预算；约束条件式（3）为广告客户所要求达到的最小广告播放数；式（4）是所投放的广告无法超过某个广告屏的广告容量。N为广告客户总数。利用大数据和定位技术获得对应广告屏覆盖的受众数据，覆盖率的高低反映了户外广告和周边客流量的相关程度。如果覆盖率低，说明广告和周围客流的偏好属性相关程度小，在这类广告屏上就要尽量少投放广告；如果覆盖率高，说明广告和广告屏周围客流偏好属性相关程度大，在这类广告屏上就要尽量多投放广告。

2 对户外广告资源配置优化问题的求解

本文的优化目标是基于某种户外广告预算，广告商全部收入最大化。需要解决的问题是通过算法提升运行效率，实现对于最优值的搜索与求解。

2.1 粒子群优化算法

粒子群优化算法（particle swarm optimization，PSO）主要依据鸟类群体的相关行为作为基础进行研究，同时根据相关的生物模型进行进一步优化[5]。这种算法以整体为参考，从而消除了个体之间的差异。算法将测量的个体粒子化，在空间中对相关的性能指标进行测量，并按照群体的状况作动态调整。

所有粒子现在的最好位置 P b可通过下列式子来确定：

每个粒子位置的各维值按式（8）和式（9）进行动态调整。

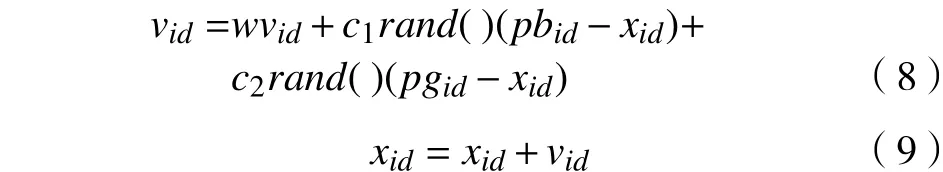
式中：w为惯性因子；为介于（0, 1）之间的随机数。

2.2 引力搜索算法

引力搜索算法（gravitational search algorithm，GSA)是以万有引力为基础的一种基本算法。在一个空间中，粒子之间的作用受到万有引力的影响，并且具有一定的指引作用，同时在所有的相关粒子之间会产生一种奇特的现象，即对于整体中质量最大的粒子，会产生一种相当于人类所说的“人格魅力”，不断地去吸引其他的粒子[6-7]。与PSO相似，这种算法在多维空间中进行相关的初始化过程时，一般对于其惯性质量有固定的公式进行计算，根据下列式子得出相关数据：

在搜索空间的不同维数中，粒子的引力

依照牛顿万有引力定律，粒子i在d维空间上的合力与别的所有粒子对它的作用力的和是完全相同的。

要想提高算法的随机性，将粒子i受到的全部作用力进行随机化，这时粒子的加速度

在群体的进化环节里，粒子依照以下方程进行相应的改变。

2.3 混合粒子群算法

对于本文的优化问题，粒子群优化算法具有一定的优势，同时也有相关的劣势存在，它主要是在前期的相关运算中表现出很强的优化能力。但随着运算的进行，相关的优化收敛速度会有所下降，到后期就会有衰退的现象。所以，无法保证整体性的优化，容易陷入局部最优。通过结合上述引力原理进行优化融合，刚好填补了粒子群优化算法在后期容易陷入局部最优的劣势，将两种方式进行整合优化，能够达到最优的效果，对于整体优化有很好的优势，并能够进行广泛运用[8]。混合粒子群算法（hybrid particle swarm optimization，HPSO）步骤如下：

a. 初始化算法的相关系数；

b. 随机初始化粒子群所处位置；

c. 求各粒子的最佳值；

d. 寻找个体历史最优解与全局最优解；

e. 使用PSO算法更新粒子速度和所处位置；

f. 若粒子群的进化停滞步数大于设定值T，那么，转入步骤g，否则，转步骤h；

g. 采用GSA进行优化搜素，更新个体历史最优解和全局最优解；

h. 若符合搜索精度或者达到最大搜索次数，那么，进入步骤i，否则，搜索次数提高一次，且进入步骤c，进行下一次的搜索工作；

i. 输出全局最优解和最优个体值。

2.4 协同混合粒子群算法

协同进化概念最早由Ehrlich和Raven共同提出，讨论的是植物与蝴蝶在进化过程中的相互影响，这种相互作用方式在大自然中特别是在相互的生存依赖方面，是一种普遍存在的关联关系。通过双方的共同努力、共同生存及进化，很好地体现了物竞天择、适者生存的自然生存法则。

这种相互作用和进化的方式，要求充分掌握与个体关联的其他个体的各类信息数据，体现了个体与整体之间的相关性，而不仅仅由定义目标个体的函数来评价个体。通过对自然界的各类相互作用进行观察和研究后，Jason也提出了相近的协同进化理论，内容不仅涵盖了生物间的竞争关系、寄生依存关系，同时还包括了捕食者和被捕食者之间存在的相关关系，以及互利的协同进化[9]，基于并行与相互合作，协同进化算法提升了运行效率，减少了计算时间，提高了种群的精度，实现对于最优值的搜索。

由协同进化理念演变而成的算法最主要的特点是在搜索时通过多个种群并联运行，而在后续迭代时设置各类差异性的进化，这种方法不仅对全局整体搜索起到效率提升作用，并且还能对后期所获的最优值进行迅速收敛。在搜寻运行过程中，种群之间建立起一个不断相互进化影响的机制，从而有效地解决了陷入局部最优的问题，能够取得更好的辨识效果[10]。

在协同混合粒子群算法（cooperative hybrid particle swarm optimization，CHPSO）中，将粒子群平均划分为k个子群，每个子群首先独立，并行完成寻优过程，通过子群交流获得种群的最优粒子，并用该最优粒子随机替换各子群中的一个粒子（最优粒子所在子群除外）。协同混合粒子群算法流程如图1所示，其步骤主要包括：

a. 初始化参数，初始化种群；

b. 将种群平均划分为k个子群；

c. 各个子群利用HPSO算法寻优，HPSO流程如图2所示；

d. 子群交流，种群最优粒子与最优适应值更新；

e. 利用种群最优粒子随机替换各子群中的任一粒子（最优粒子所在的子群除外）；

f. 当满足搜索精度或达到最大搜索次数，则优化过程结束，否则转步骤c。

M为惯性质量，a为加速度，G为引力参数，b为最好适应值，w为最差适应值。

图1 协同混合粒子群算法流程图Fig.1 Flow chart of the cooperative hybrid particle swarm optimization

3 仿真实验及分析

实验是在Matlab 2015R软件下运行，对本文所提出的优化问题进行分析。假设目前有20个有意向的客户需要进行广告的播放，只有10个合适的广告屏幕，并且对于每组的相关数据按500次的数量来进行计算。由于户外广告客流量偏好属性以及定位的统计数据涉及行业保密性，不便公开，在此借鉴文献[11-16]，在实验环境下使用上述方法来生成不同广告在不同广告屏上的播放，并且和文献[16]维持同样状态。这里参数调整如下：的 大小取值控制在0～200之间，是20～800之间均匀分布的任意数字，gij为第i个客户在第j块广告屏时的引力参数，0.4pij，Mi取70～400之间均匀分布的任意数字，Ci取500 000～2 000 000之间均匀分布的任意数字，Sj取2 000～4 500之间均匀分布的任意数字。

CHPSO算法的相关系数调整为：协同子群个数为5，最大迭代次数为20 000，种群大小N=100，学习因子c1=c2=2，惯性权重w=0.7，PSO算法的进化停滞步数T0设定值为50，当停滞步数大于T0时，引入 GSA算法寻优。GSA中 G0=100，α=20。对仿真实例分别进行10次独立实验，通过一系列的计算，得知最优解为4.233 9×106，也就是所有广告在屏幕上的呈现次数，如表1所示，该最优解体现了算法的科学性与合理化，如图3所示。Fi为适应度函数值，g为迭代次数。

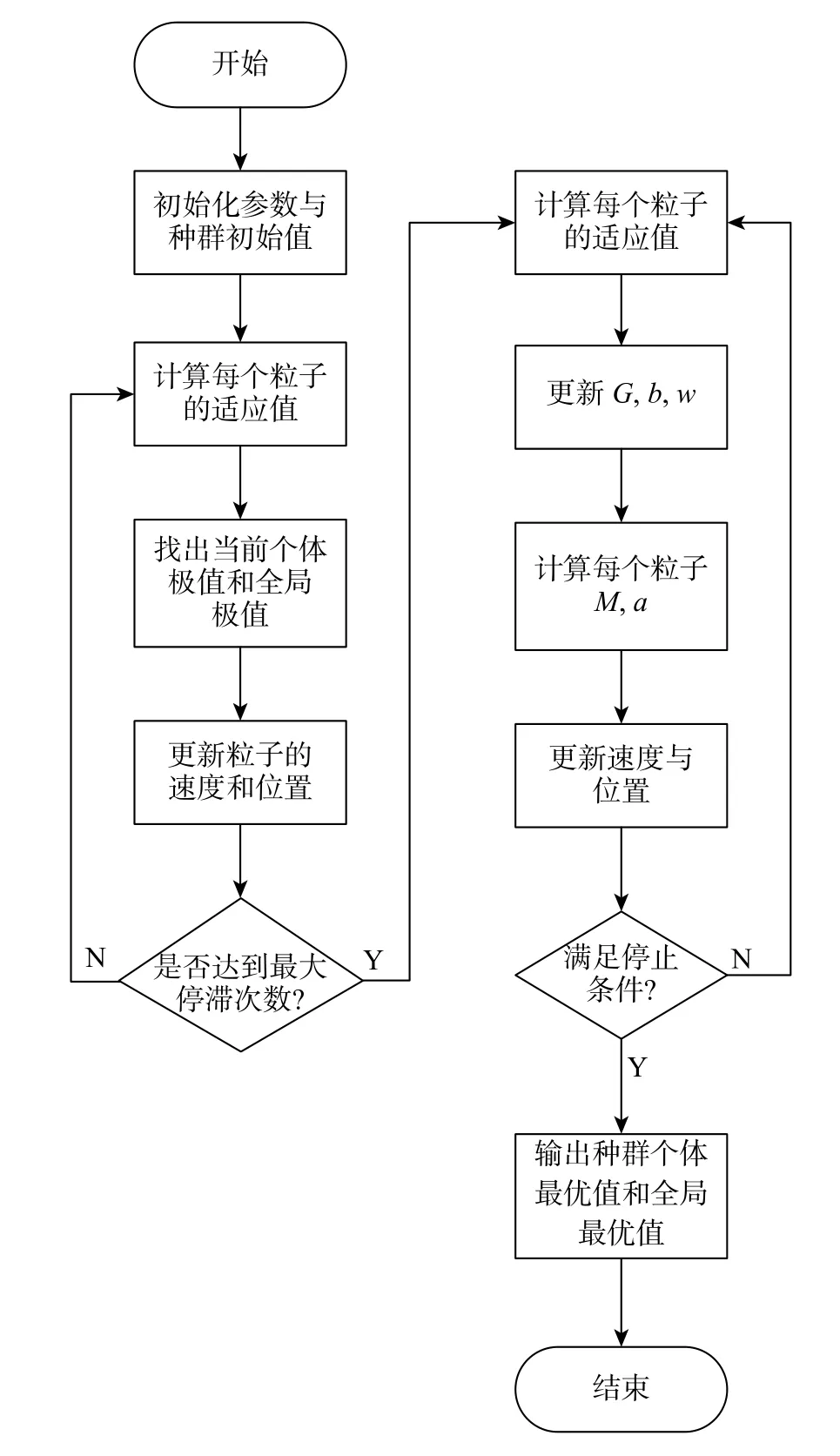
图2 HPSO子流程图Fig. 2 Sub flow chart of the hybrid particle swarm optimization

图3 算法性能Fig.3 Algorithm performance

表1 算法最优解Tab.1 Optimal solution by the algorithm

4 研究结论与展望

本文模型是一个带约束的整数优化解决方案，通过罚函数将其转换为无约束问题，并以融合优化的方式进行最优求解，相关的仿真实验结果表明了协同混合粒子群算法的有效性。

提出了一种基于大数据与定位技术精准营销相结合来进行综合定价的模型。将这种模型运用于户外广告领域，能够较好地解决广告主和相关广告运营企业的共同利益互存，使双方的利益最大化，具有实用性，其主要体现在3个方面：

a. 移动互联网技术及大数据技术的发展，使户外媒体受众的各类行为数据得以像互联网媒体一样被收集与挖掘，使户外媒体的精准营销成为必然趋势，此模型在广告主及媒体运营商两方效益共同提升的可能性方面进行了探索。

b. 户外媒体的受众主体行为目前仅依靠单位时间内的观测法、调研法及摄像监控进行统计，缺乏科学的数据统计方法，在此基础上进行数据挖掘，导致户外媒体的选择与广告效果的评估均存在较大漏洞。本文提出的户外广告资源配置优化模型为户外广告效果提供了新的判断方法。

c. 线上数据与线下场景如何进行导流互通，这是户外广告资源优化配置中较为关键的问题，现在的问题是导流过程中缺乏数据。目前户外的数据只有车流、人流，缺少一个能够贯通其他平台的数据解决方案。未来，户外能否采用和移动互联同一基础的数据来评估，或者提供户外的受众数据、人数以及画像，从而形成真正有效导流的方法还有待进一步研究。

本研究提出的户外广告资源优化模型能较有效地解决广告客户和媒体运营商的利益平衡问题，更适合实际应用情况。模型是一个带约束的整数优化问题，通过罚函数将其转换为无约束问题，并通过协同混合粒子群算法进行求解，仿真实验结果表明了算法的有效性。