圆内开缝圆环形空间自然对流的格子Boltzmann模拟

余端民，赵 明

（上海理工大学 能源与动力工程学院，上海 200093）

对于自然散热的封闭电流母线，为了强化环形空间内的对流换热，现有研究常将内圆筒沿竖直方向开缝，构成了内圆筒开缝的封闭电流母线，其所抽象出的理论思想即为圆内开缝圆环形空间自然对流换热问题。当内圆开缝时，内圆包围的区域和外圆包围的区域连通在一起，所以开缝圆内部也存在流体流动，同时其内外壁面都参与换热，这不仅增加了环形空间内流动换热的复杂性，更增强了几何结构和物理参数对流动换热不稳定性的影响。研究这种特殊结构空间内的自然对流换热，获得其中的流动和换热规律，不仅为传热学理论研究提供参考，更为复杂的工程问题提供数据支撑和理论指导。

1 国内外研究现状

圆内开缝圆环形空间的物理模型可归结为封闭空间自然对流换热问题，该问题普遍存在于换热器和电气领域中，国内外研究者们已进行了大量研究。其中，水平同心圆环的自然对流换热最具有相关性。Powe等[1]用烟可视化技术研究了不同半径比的水平同心圆环内自然对流的流型，首次得到了稳态流型、多胞流型、三位螺旋流型和二维振荡流型烟可视化照片，为以后的数值模拟和实验提供了参考依据。Morgan等[2]通过实验获得了圆环内自然对流的努塞尔数Nu实验关联式。Kuehn等[3]用实验和数值模拟两种方法研究了圆环内自然对流的流动换热特性，并且数值模拟结果与实验结果吻合较好。Petrone等[4]以多种数值模拟方法分析了不同半径比对圆环内自然对流的影响，得出了流型转化的临界瑞利数Ra会随着半径比的减小而随之减小的结论。除水平同心圆环外，Projahn等[5]和Chao等[6]研究了带一定偏心率的双圆环结构的自然对流；Djezzar等[7]用有限体积法模拟了共焦椭圆环内的自然对流；Xu等[8]模拟了圆环内三角形内Ra、半径比和三角形倾斜角度对稳态自然对流的影响。

本文研究的圆内开缝圆模型和以上模型相比，是在水平同心圆环的结构上对内圆对称开缝，相比其他水平封闭空间的自然对流换热，数值模型更加复杂。其最显著的特征是，当Ra在某些取值范围内时，存在自然对流换热的不稳定性。对于自然对流不稳定性方面的研究，已有较多成果发表。如Cimarelli等[9]采用直接数值模拟方法研究了不同Ra对竖直流道内流体流态的影响；Gallegos等[10]用格子Boltzmann方法模拟了偏心球内的自然对流现象，分析了Ra和偏心率对球环内流体流态和平均Nu的影响。而对于圆内开缝圆自然对流换热的研究，早期的研究者多是采用传统实验或有限容积数值方法对其自然对流换热特性进行研究。如Kuleek[11]通过双环流近似模型提出了近似的换热公式，其后，王国祥等[12]通过环形电流母线实验得到了Nu实验关联式，他们的研究都证实了内圆开缝能够强化换热。文献[13-14]最早对圆内开缝圆自然对流的不稳定性进行数值分析，他们主要从数值模拟的多解性和流动换热的非线性特性展开研究，采用二维SIMPLE算法QUICK格式模拟了稳态情况下的自然对流，发现相同结构参数下流场和温度场也会出现多解性。黄夫泉等[15]和Shen等[16]数值研究了不同开缝度对圆内开缝圆自然对流换热特性的影响，Zhang等[17-18]采用二维和三维的数值模拟方法，并通过实验分析了圆内开缝圆自然对流现象。他们的研究结果表明，低Ra时，二维和三维数值结果和实验结果吻合得很好，但Ra较大时，二维数值与实验结果的差异趋于增大，三维数值结果仍能很好吻合。

上述研究都是基于传统的数值研究方法，近年来发展的格子Boltzmann方法由于其物理意义清晰、边界处理容易、演化过程清楚、程序易于实现、并行性好等优点逐渐受到人们的关注，不少学者采用该方法在研究封闭空间自然对流换热方面取得了一些成果。Yang等[19]基于格子Boltzmann方法数值模拟了圆内开缝圆自然对流换热，给出了温度场随不同Ra和开缝度的变化情况。Shi等[20]用基于有限差分的格子Boltzmann方法获得了水平双圆环内Ra在一定范围内的速度和温度分布以及Nu，模拟结果不仅与已有结果相符合，而且表现出了更好的数值稳定性。Fattahi等[21]和Luo等[22]用格子Boltzmann方法模拟了半径比、Ra和普朗特数Pr一定时不同位置的内圆对偏心圆环内自然对流的影响。Mehrizi等[23]用格子Boltzmann方法模拟了圆内三角形自然对流，结果表明，下移的三角形能强化换热，上移或左右移动换热效果明显降低。

本文拟采用耦合热格子Boltzmann模型对圆内开缝圆环形空间内对流换热进行进一步的数值研究，主要分析Ra和开缝度对环形空间内流动换热的影响，以及流型随Ra、开缝度变化的转变过程。

2 物理模型及格子Boltzmann方法

圆内开缝圆环形空间自然对流换热的物理模型是从水平放置的内筒开缝的封闭电流母线所抽象出来的二维模型，其示意图如图1所示。图中：ri为开缝圆内径，ro为外圆内径，两内径比为为内部圆环厚度且满足；开缝度定义为为开缝处夹角的一半；内外圆壁面分别维持在恒定温度Ti和To，且Ti＞To；A为无量纲温度监测点；L为特征尺度；设定封闭圆内流体的Pr数为0.7，满足Boussinesq假设；g为竖直向下的重力加速度。

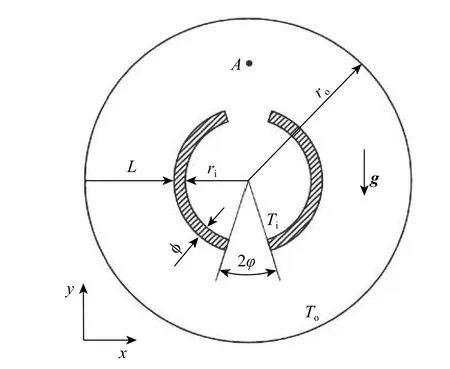
图1 物理模型示意图Fig.1 Schematic diagram of the physical model

格子模型采用Guo等[24]基于Boussinesq假设提出的耦合热格子模型——CLBGK模型。但本文的温度场采用具有更高计算精度的D2Q9速度离散模型，在复杂边界条件下更能保证数值模拟精度。其密度分布函数和温度分布函数的演化方程为

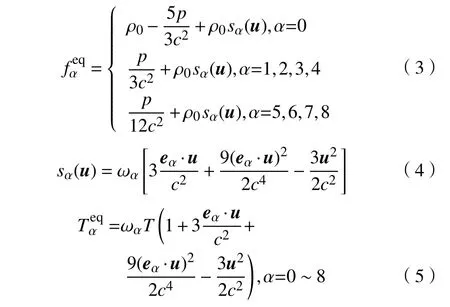
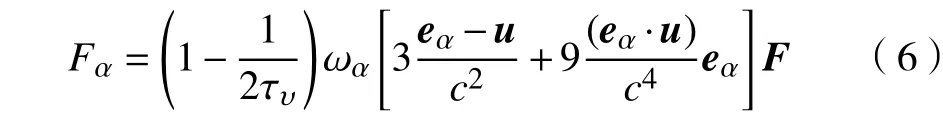
假设流体不可压且忽略黏性热效应,为了包含由温度差引起的浮升力项，引入Boussinesq假设，则浮升力F为

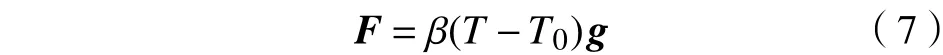
通过Chapmann-Enskog多尺度展开可得如下Boussinesq宏观方程组

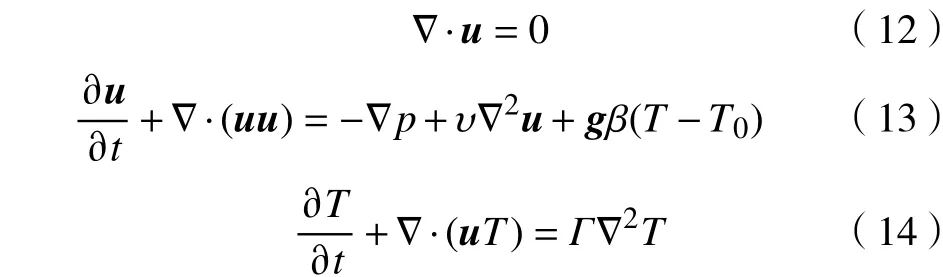
式中，运动黏度υ、热扩散系数Γ、无量纲松弛时间 τυ，τT满足如下关系

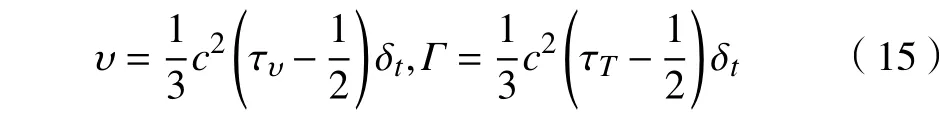
曲边界处理方法采用Guo等[26]提出的非平衡态外推格式和空间插值相结合的曲线边界处理方法，其基本原理是把边界格点的分布函数分解为平衡态和非平衡态两部分，平衡态部分用虚拟的平衡态分布函数代替，而非平衡态部分由相邻流体节点的非平衡态部分插值确定。

3 程序验证

为了验证模型，本文以水平同心圆环间的自然对流作为算例，并与文献[3]采用有限差分法的模拟结果进行了对比验证。在相同条件下，等温线、流线分布对比如图2所示，Ra=5×104，Pr=0.7时径向无量纲温度分布对比结果如图3所示。由图2～3可知本文结论和参考文献[3]所得结论吻合较好，验证了本文模型的准确性。

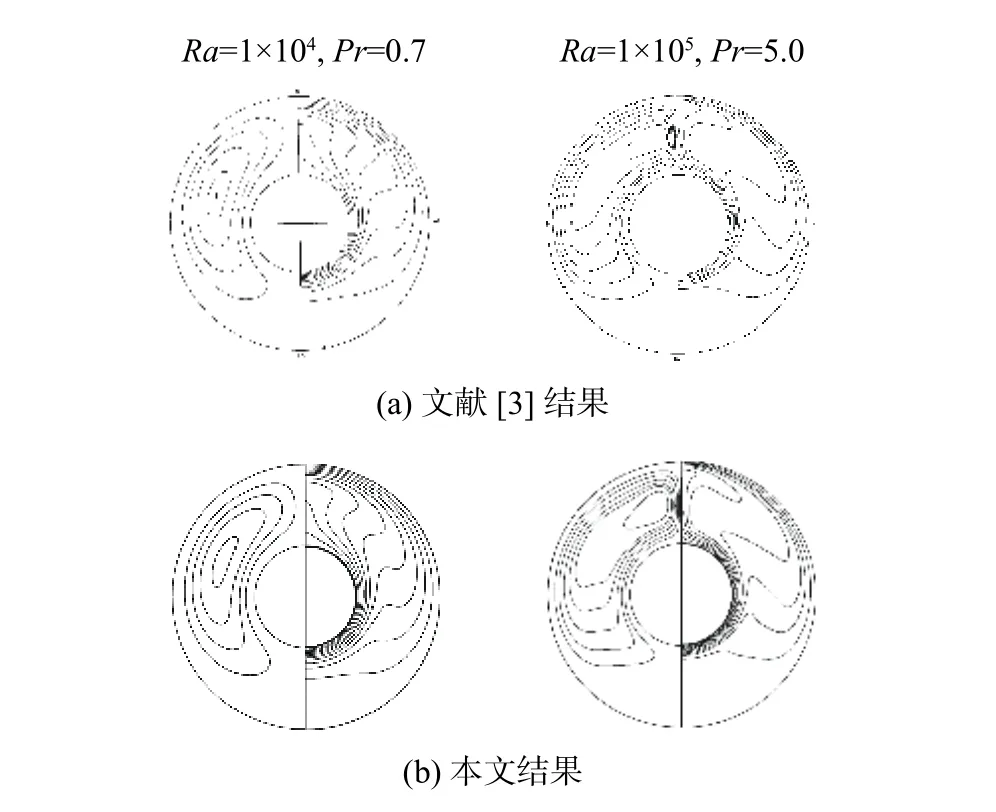
图2 流场（左）和温度场（右）分布图对比结果Fig.2 Comparisons of the flow field（ left） and temperature field （right） distribution

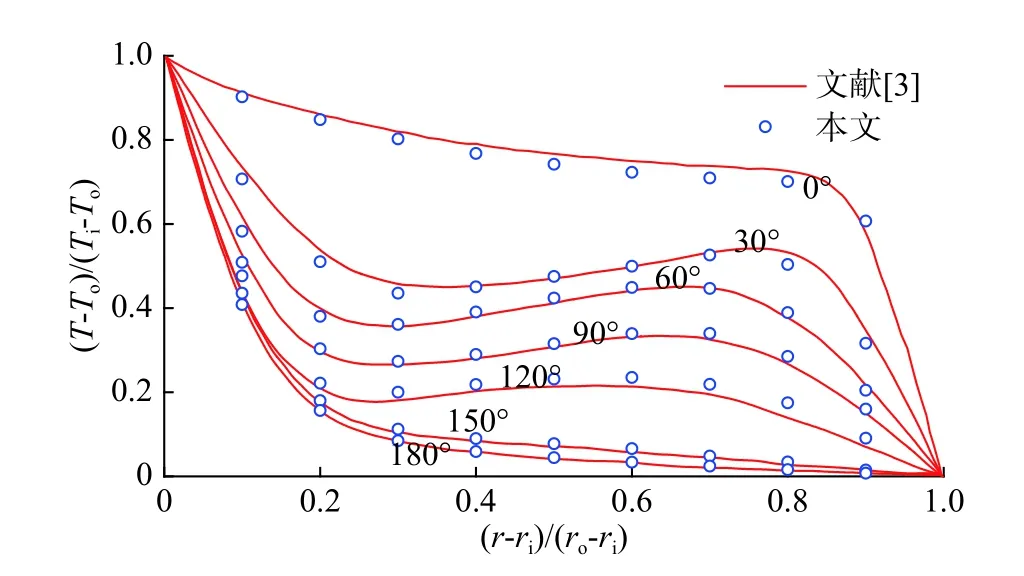
图3 径向无量纲温度分布对比图（Ra= 5×104，Pr=0.7）Fig.3 Comparison of the radial dimensionless temperature distribution at Ra=5×104, Pr=0.7

4 结果分析

4.1 Ra对流动和换热的影响

图4所示为开缝度S=0.3，不同Ra下，圆内开缝圆环形空间内温度场和流场分布图，而图5是相同参数下对应的监测点无量纲温度随时间t的变化情况。从图4可观察到，不同Ra下自然对流换热所对应的温度场和流场均有所不同，但是发生变化的主要是环形空间上部，下部几乎保持不变。这是由于密度小的热流体上升，并在环形空间上部进行对流换热，使温度场发生变化；而密度大的冷流体沿外壁面不断下沉，在下部形成流动滞止区，滞止区内以导热为主，所以下部温度场呈现稳定的分层结构。从图4（a）可观察到，当Ra较小时（Ra=1×104），环形空间上部外壁面近壁处还未形成明显的边界层，等温线在壁面附近近似均匀分布。这是因为此时自然对流强度较小，开缝圆上部流动强度较弱，流体间的传热方式以热扩散为主（由图4（b）所示）。此时，流体沿开缝圆热壁面上升，沿外圆的冷壁面下降，形成两个较大的弱涡卷，且左右涡卷沿中心轴线对称，不随时间变化，这种流型称之为稳定的二涡流。

同样，从对应参数下无量纲温度监测变化图5（a）可看出，监测点无量纲温度增大到一个固定值就不再随时间发生变化。随着Ra逐渐增大到4×104时，浮升力增强，开缝圆上部流体流动强度增强，流体间的传热方式以热扩散逐步向热对流转变，外圆壁面附近开始形成明显的边界层。此时，外圆壁面附近的冷流体沿中轴线下降并在开缝口随热流体上升，在开缝圆的上方形成两个逆时针旋转的“二次涡”，说明流型已转变为四涡流型。由于冷流体的下降，外圆壁面附近等温线曲折，使得监测点温度和外壁面附近的流体温度在一个等温线上，同时监测点的无量纲温度也明显低于二涡流型时的无量纲温度，并且由于流动的不稳定，监测点温度也随时间振荡，如图5（b）所示。当Ra进一步提高到1×105时，热浮升力进一步增强，自然对流不稳定性加剧，原来的四涡流型发生结构上的改变，表现为二涡流型和四涡流型相互转变的情况，两种流态交替出现，此时监测点无量纲温度振荡也是加剧的（如图5（c）所示）。在Ra=1×106时，在强烈浮升力的作用下，外圆近壁面处的等温线密集，流体沿开缝圆内外热壁面上升至外圆的冷壁面，最后沿冷壁面直接下降，环形空间内形成两个大的不稳定的涡卷，两个涡卷一大一小且随时间相互转变，这种流型称之为振荡的二涡流。此时开缝圆上部的等温线也出现周期性地左右偏斜，不再对称。图5（d）的监测点温度变化情况也反映了这种振荡的二涡流型特性。

综上分析，因开缝圆和环形空间连通，开缝圆内外壁面都参与换热。一部分流体沿开缝圆外壁面上升；另一部分流体由开缝圆底部流入，沿开缝圆内壁面上升，至顶部开缝处后，沿外圆的冷壁面下降，会形成环形自然对流。但由于自然对流的不稳定，随着Ra增大，环形空间内主要有4种基本流型：稳定的二涡流、四涡流、二涡流和四涡流之间振荡的交变流以及振荡的二涡流。

图4 开缝度为0.3时不同Ra所对应的温度场和流场分布Fig.4 Temperature field and flow field distributions for different Rayleigh numbers at slotted ratio of 0.3

图5 开缝度为0.3时不同Ra下无量纲温度随时间的变化Fig.5 Time variation of the dimensionless temperature for different Rayleigh numbers at the slotted ratio of 0.3

4.2 开缝度S对流动和换热的影响

为了研究开缝度S对流动换热的影响，Ra=7×105保持不变，而开缝度分别取为S=0.1，0.2，0.3，0.4。图6为不同开缝度环形空间内温度场、流场的分布图，图7为不同开缝度下监测点无量纲温度的变化图。由图6可知，在Ra一定时，不同开缝度下环形空间内也主要存在二涡流和四涡流这两种基本流型，但是流型转变的顺序发生了变化。首先当开缝度从0.1增加到0.2时，开缝度的增大增加了通过开缝处的流量，使开缝圆内更多的热量被携带到环形空间上部参与对流换热，环形空间内的自然对流增强，致使原本稳定的上升流发生左右振荡，振荡的流场引发温度场和监测点无量纲温度也发生振荡。当开缝度进一步增加到0.3时，沿两热壁面上升的热流间距也增大。热流间距较大时，在两股热流间就会形成低流低温区，在靠近外冷壁面的流体主要通过热扩散的方式进行传热。当热流体传递的热量大于冷壁面传过来的冷量时，冷流体较少，低流低温区保持为上升流，此时环形空间内主要是二涡流型；当热流体传递的热量小于冷壁面传过来的冷量，冷流体增多，增加到某个临界值时，密度大的冷流体就会冲破低阻力的低流低温区下沉至开缝口附近。由于下降的冷流体被加热以及开缝口阻力大，冷流体又附着热流一起上升，形成两个逆时针旋转的“二次涡”，使流型转变为四涡流。从图7（c）的监测点无量纲温度随时间的变化情况也可以看出，小幅波动的温度会突然向下跌落。这里向下跌落的原因就是因为冷流体的下降，但是监测点的温度主要还是维持在小幅振荡的情况，说明此时环形空间内的自然对流虽然减弱但仍较强。当开缝度增加到0.4时，低流低温区随热流的间距增大而增大，同时开缝口附近的阻力变小，如流场分布图6所示。下降的冷流体一部分在上开缝口附着热流一起上升，另一部分穿过开缝圆进入环形空间下部，经换热后再沿着开缝圆内壁面上升。由于冷流体流入开缝圆内，从开缝口上升的热流体减少，环形空间内自然对流相对减弱，外壁面附近冷流体增多，冷流体下降次数也随之增多，所以流型在二涡流和四涡流之间的转变更加频繁，同时监测点的温度跌落也更加频繁（如图 7（d）所示）。

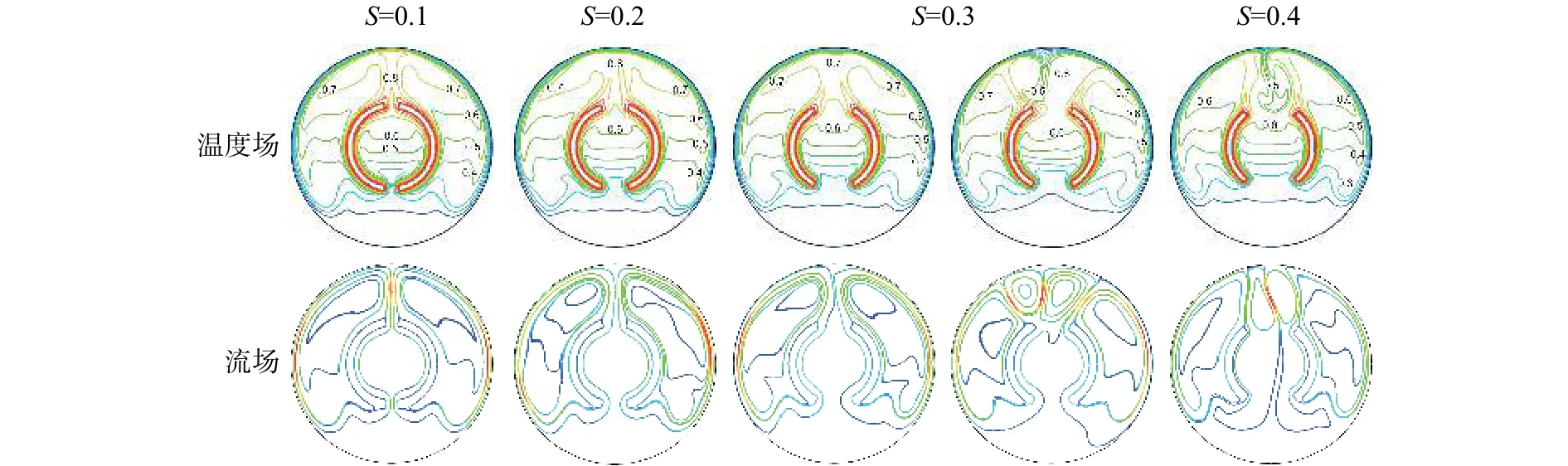
图6 Ra为7×105时不同开缝度所对应的温度场和流场分布Fig.6 Temperature field and flow field distributions for different slotted ratios at the Rayleigh number of 7×105

4.3 开缝度和Ra对流动换热影响的综合分析

通过以上单一条件下Ra和开缝度对圆内开缝圆环形空间内流动换热影响的分析，可以发现Ra和开缝度都会引发环形空间内流动型态的转变，图8示出了不同Ra和开缝度下所对应的流动型态全图。从图8可看出，不同开缝度下环形空间内流型都是从稳定的二涡流向振荡的二涡流转变，但是转变的过程不尽相同。当S=0.1时，环形空间内只存在二涡流型，Ra=8×105时，稳定的二涡流直接转变为振荡的二涡流；当S=0.2时，稳定的二涡流在Ra=8×104时转变为二涡流和四涡流之间振荡的交变流，在Ra增加到Ra=6×105时，交变流又转变为振荡的二涡流；当S=0.3时，环形空间内出现了4种流动型态，在Ra=1.45×104时，流型先从稳定的二涡流转变为四涡流，然后四涡流过渡到二涡流和四涡流之间振荡的交变流，最后当Ra=8×105时发展为振荡的二涡流；S=0.4时，环形空间内也存在4种流动型态，但此时四涡流存在的Ra区间明显小于开缝度为0.3时的区间，且交变流转变为振荡的二涡流的Ra也增大到Ra=9×105。从流型的转变过程可以发现，在不同开缝度下流型的发展都存在一个上下临界RaRacr。当Ra大于下临界Racr时，稳定的二涡流会向其他流型转变；当Ra大于上临界Racr时，其他流型就会转变为振荡的二涡流。如图8所示，用虚线和实线分别连接不同开缝度下流型转变的上下临界Racr，从下临界Racr的变化趋势可看出，开缝度S=0.1到S=0.3时，流型转变的下临界Racr数随开缝度增加而不断下降。但是，当S=0.4时，下临界Racr数反而增加了。由此可知，在开缝度S＜0.3时，开缝度越大流体的流动型态更易受Ra的影响，当开缝度S＞0.3时，Ra对流型的影响随开缝度增大而减弱。同样随开缝度增大，上临界Racr也经历了先减后增的变化趋势。但是，上临界Racr最低点在S=0.2，说明在S=0.2时达到强自然对流的Ra最小，环形空间内对流换热强度最大。所以Ra一定时，增大开缝度能增加环形空间内自然对流换热，但不是开缝度越大越好，而是存在一个最佳的临界值。

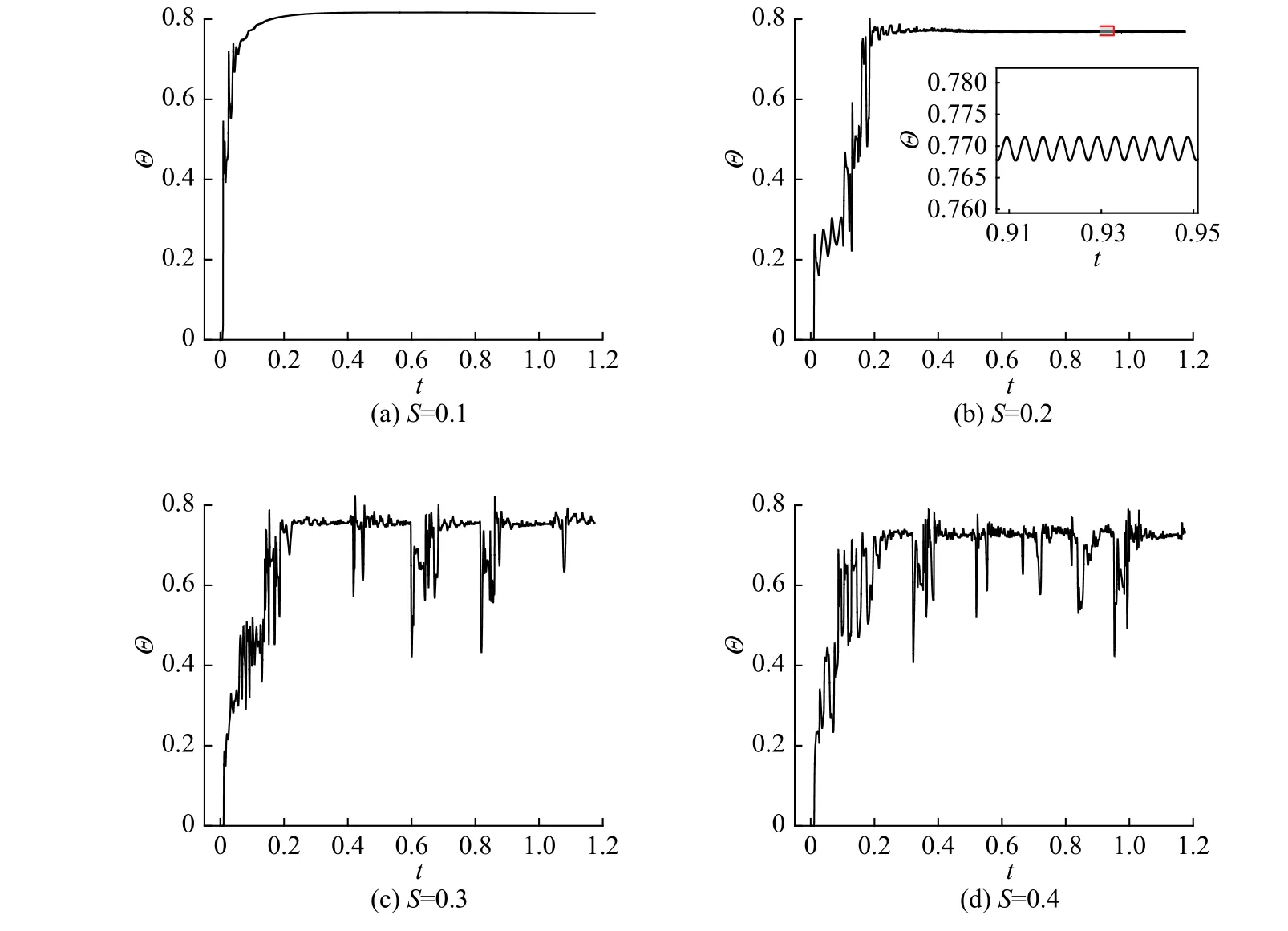
图7 Ra为7×105时不同开缝度下无量纲温度随时间的变化Fig.7 Time variation of the dimensionless temperature for different slotted ratios at the Rayleigh number of 7×105

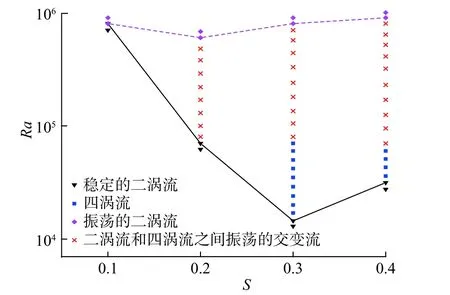
图8 不同Ra和开缝度所对应的流动型态Fig. 8 Flow patterns corresponding to different Rayleigh numbers and slotted ratios

5 结 论

本文采用热格子Boltzmann方法对圆内开缝圆环形空间自然对流换热进行了数值模拟，分析了Ra、开缝度对环形空间内自然对流换热的影响，获得如下结论：

a. 随Ra增加，环形空间内自然对流换热会出现较强的不稳定性，流型转化也较丰富，存在4种流型：稳定的二涡流、四涡流、二涡流和四涡流之间振荡的交变流以及振荡的二涡流。

b. 开缝度的改变对环形空间内自然对流换热影响是显著的。随着开缝度的增大，流体会形成多涡流型，增强流体扰动，流动不稳定性增强；而且在不同开缝度下，流型的发展都存在一个上下临界RaRacr，当Ra大于下临界Racr时，稳定的二涡流会向其他流型转变，当Ra大于上临界Racr时，其他流型就会转变为振荡的二涡流。

c. 适当增大开缝度能增强环形空间内自然对流换热，但不是开缝度越大越好，而是存在一个最佳的临界值。