基于相位恢复的二维图像彩色再现

孟春丽，王海凤，刘韵杰，曾大奎

（上海理工大学 光电信息与计算机工程学院，上海 200093）

光线被物体反射，载有物体信息的光波包含了振幅信息和相位信息，与振幅平方成正比的光强可通过图像传感器记录，如CCD（charge coupled device） 或 CMOS （complementary metal oxide semiconductor），即物光衍射波的振幅信息可轻易获得，却无法采集相应光束的相位信息。相位信息描述了强度分量的偏离程度，所以在光场衍射计算中，如若缺失了相位信息，光强信息的传递就得不到预期结果，所以获取光的相位信息尤为重要。

相位恢复方法有干涉和非干涉检测两种，其中干涉检测相位主要有全息术[1]和剪切干涉法[2]。而干涉对空间和时间相干性和干涉条纹的分辨率要求较高，投影介质不稳定、激光成像的噪声控制困难等原因难以得到高分辨率的显示，此外复杂的结构系统都使其应用发展不及非干涉检测方法。非干涉检测方法主要包括迭代法、光强传输方程法（transport of intensity equation，TIE）[3]。迭代方法基于GS(Gerchberg-Saxton)算法[4]等，后续修正发展出许多相关迭代算法。其中，混合输入输出法和杨国桢-顾本源算法[5]应用最广，该方法通过测得几面光强的限制使误差减小，但初始值选取随意，迭代时间长。通过测量数个轴向光强面并利用TIE解得相位的方法应用简单，各种求解方式主要有格林函数[6]、泽尼克多项式[7]，以及傅里叶变换方法[8]，其中傅里叶变换方法效果较好，但因计算的多次近似导致其恢复所得相位精度不高。结合TIE法和迭代法，将由TIE解得的相位作为迭代法的初始相位，这样既可加快收敛速度，又可提高TIE算法的精度。

本文采用快速傅里叶变换方法求解TIE方程，将复杂的微分方程转换成代数方程，灵活快速，更适于Matlab编程处理。利用近场衍射模拟的光强截面，将TIE计算所得初始相位和模拟光强分布代入基于GS迭代的角谱传递算法中进行循环迭代。这样结合二者优点的混合迭代算法[9]一方面避免了迭代中初始相位选择的随机性带来收敛慢的缺点，另一方面提高了TIE算法的精度问题，得到较高精度的相位恢复效果。对于记录位置的光强分布，通过计算相位和角谱传递函数，结合图像的 RGB（红（R）、绿（G）、蓝（B））通道，可获得像面附近任意位置的彩色图像光强分布。

1 算法原理

全息方法可以记录衍射波的相位分布，但干涉法恢复相位要求物光和参考光具备较高的相干性，而且实验仪器精密复杂，因此对成像环境要求很高。非干涉恢复相位方法有TIE方法、迭代法以及相空间法[10]，其中相空间法计算冗余量大，使用度不高。考虑到TIE和迭代方法各自的缺陷，结合TIE方程和优化加速的GS迭代算法可以提高相位恢复精度和加快收敛速度。

1.1 光强传输方程

光强传输方程TIE最早由Teague[3]提出，描述的是光场成像过程中，衍射波传播方向的光强轴向梯度与垂轴方向相位分布间的关系。求解TIE的方法中，快速傅里叶变换方法可以简单有效地恢复相位，但所得相位图精度不高。在求解TIE过程中，可利用角谱传递函数，模拟物光衍射波在像面Ib附近的成像光强分布Ia和Ic。图1为成像面附近的三面光强分布，与像面间距分别为Δz1，Δz2，三面光强的复振幅分布可分别表示为

式中：Ua，Ub，Uc分别为负离焦面、成像面、正离焦面的光场复振幅；A1，A2，A3为对应面的振幅分布；kx，ky，kz分别为光矢量k在x，y，z方向的分量；z为光场传播方向，即光轴坐标；x，y为垂直于光轴的平面坐标；z1， z2，z3分别对应Ia，Ib， Ic光强面在z轴的位置；j为虚数单位，j2=-1；φ1，φ2为离焦面相对于像面的位相变量。

图1 光场衍射中的三面光强分布Fig.1 Intensity distribution on three planes along optical axis

利用光强传输方程（4），设等式右边除负号外的算式为T，根据亥姆霍兹定理[11]将等式左边矢量场分解为标量函数的梯度和矢量函数的旋度之和，见式（5）。其中，与都是辅助函数，引用 Teague近似，忽略式（5）的旋度项，得到，为梯度算子。对式（4）两边进行快速傅里叶变换fft，由傅氏变换的微分性质（6）[12]，f（n）表示函数 f的 n 阶导数，解得的值，见式（7），ifft表示快速傅里叶逆变换。由式（5）可知，再次利用傅氏变换的微分性质，求解最终可得到光强传输方程的解，如式（8）所示[3]。

1.2 混合迭代算法

在离焦距离较小时，TIE方法的恢复效果较好，而角谱迭代算法应用范围更广，尤其对大离焦以及高频信息方面更有优势[13]。为解决迭代方法收敛慢的问题，将TIE计算出来的相位轮廓作为角谱迭代方法的初始相位，这样结合二者的优势，弥补彼此的缺陷，得到更优的算法，使恢复相位的范围更大，效果更好。

将上述TIE计算所得的b面相位作为初始相位Pb，结合模拟的b面振幅Ab，作为初始迭代面的复振幅Ub代入迭代，利用快速傅里叶变换转换到频域进行处理[14]，将其频谱乘以b，c面间距离Δz2对应的角谱传递函数，再进行傅里叶逆变换即可得c面的复振幅分布。通过对其求相位角以及记录所得的c面振幅Ac，重新构成c面的复振幅Uc。对其在频域中进行角谱逆向传递，方法同第一步一致，如此每步用记录所得的振幅替代传播后计算所得的振幅加以校正。由此，衍射波传播过程记录的3个面形成一个循环，在传播到每一面时，用该面记录所得的振幅结合计算的光场传播到该处的相位组成复振幅，这样可以校正光场角谱衍射迭代中的偏差，将实验测量数据的空间关联性更好地代入迭代运算中，从而得到恢复细节更好的b面相位Pb。角谱传递函数的表达式如式（9）所示[15]。

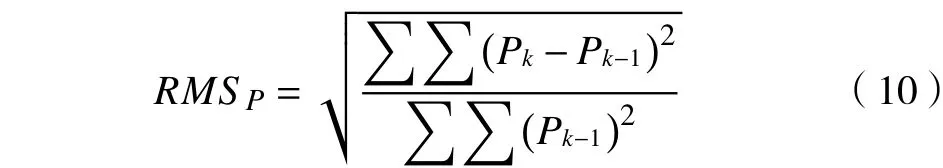
式中：RMSP表示相位的均方根误差；Pk是迭代当次的相位分布，Pk-1是上次迭代的相位分布。

2 仿真及结果分析

在Matlab仿真时，结合光束的复振幅表达形式（式（1）～（3）），利用图2所示的光强图和相位图模拟像面的复振幅分布，根据角谱传递函数式（9），通过光场衍射可得到像面附近的复振幅分布，即可获得模拟的三面光强分布，如图3所示。这三面将用作混合迭代方法中的振幅校正部分以及恢复后的对比。取仿真图像的红色通道进行说明，首先将模拟得到的3个光强分布面代入光强传输方程，计算得到模拟中间面的相位分布轮廓，如图4（a）所示。从图中可知由该方法计算所得的相位分布相较于原模拟相位，其高频部分恢复结果较差，将该结果作为GS迭代算法的初始相位，经过角谱迭代算法，可得到更加精细的相位恢复图，如图 4（b）所示。利用式（2）～（10）计算角谱迭代算法恢复相位的均方根误差为10-7，而混合迭代算法恢复相位的均方根误差达到10-8。由图4（c）可知混合迭代算法相较角谱迭代算法不仅恢复相位精度更高，且收敛更快。利用中间模拟面的光强分布和恢复的对应面的相位分布，可以重建邻近两面的光强分布，如图5所示。为了将恢复结果与图3所示的对应模拟面进行一般性比较，对第一面的模拟和重建二维图进行了差分比较，截取模拟和再现图两维数组的第256行数据，如图6（a）和（b）所示。直观上二者很相近，所以取其差值，得到误差为10-4，见图6（c），由此说明了重建光强分布的精确性。仿真中两幅模拟图像的像素分辨率均为512×512，x，y方向的采样区间长度均为5 mm。

图2 模拟光强和相位的二维图像Fig.2 Two dimensional images simulating intensity and phase informations

图3 红色通道光强分布模拟Fig.3 Simulation of the intensity distribution of the red channel

图4 分别通过TIE和GS-TIE算法得到的相位分布以及恢复相位的均方根误差Fig.4 Retrieved phase distribution by TIE and GS-TIE methods respectively as well as its root-mean-square error

图5 利用混合迭代算法重建的红色通道的光强分布Fig.5 Reconstruction of the intensity distribution in red channel by the hybrid iterative algorithm

上面阐述了红色通道的相位恢复及光强再现，通过叠加红、蓝、绿三通道恢复的光强结果，得到了彩色二维图在像面附近光强分布的彩色再现。图7为彩色光强图及与其左右相距1 mm的另外两面的彩色光强分布。通过将彩色模拟光强图分为RGB三色进行恢复再现，将三通道的光强重建图混合叠加得到对应于模拟位置的彩色像面再现，如图8所示。将重建的彩色光强图与图7所示的模拟彩色光强图进行差分来分析恢复结果的优良性。首先，分别对模拟与重建的第一面彩色光强图求取灰度，然后抽取两幅二维图的第256行数据，分别如图9（a）和（b）所示，最后对两幅图进行差分，误差结果为10-4，如图9（c）所示，由此说明了重建彩色光强分布的优良性。

图6 对应红色通道第一面的模拟图与恢复图数组的中间行分布及对应数组行分布之差Fig.6 Middle row of intensity distribution arrays at first plane in the red channel of simulated and retrieved images as well as the difference between them

图7 彩色光强分布的像面附近模拟Fig. 7 Simulation of color intensity distribution near the image plane

图8 彩色光强分布再现Fig. 8 Reconstruction of color intensity distribution

图9 对应于第一面处模拟与重建的彩色光强分布的灰度图数组的中间行分布及对应数组行分布之差Fig.9 Middle row of intensity distribution arrays at first plane in the gray-scale map of simulated and retrieved color intensity distribution as well as the difference between them

3 结 论

结合非干涉方法恢复相位中的光强传输方程和迭代算法，提高了恢复相位的精度。通过Matlab仿真了二维图像在光场成像面附近的衍射，利用衍射的仿真结果计算得到模拟相位图的轮廓，并将其作为角谱迭代算法的初始值。经过循环迭代中每个面的光强校准后，得到精确的相位分布，其相位误差均方根值低至10-8。最后，将恢复再现的三面光强分布图进行叠加得到了彩色光强分布图的再现。