考虑边界滑移的微通道热沉传热传质性能研究

宋世宇，何 磊，景大雷

（上海理工大学 机械工程学院，上海 200093）

随着系统微型化、集成化水平的迅猛发展，微尺度器件在微电子工程、微生物工程、航空航天等领域的应用越来越广泛，这对系统的散热性能提出了更高的要求[1]。目前超高性能CPU芯片的发热量可达106W/m2的数量级，与之相伴的由温度引起的元器件失效率随着温度的升高呈指数式上升。研究表明：在规定的器件工作温度范围之内，电子元器件的温度降低1 ℃，其故障发生的概率可以减少4%左右；如果超过最大规定温度值10～20 ℃，则故障发生的概率就会提高100%[2]。因此，全新的微电子器件散热技术成为当今研究的热点问题之一[3]。

20世纪80年代初，Tuckerman等[4]首先提出了微通道散热技术的构想，通过在硅片上刻蚀流道的方法加工出微通道散热器，并将其运用于电子设备的水冷散热，取得显著效果。实验发现，当水以强制对流的方式通过该微通道换热器时，最高可以带走790 W/cm2的热流量。自从这一标志性论文发表之后，微通道散热器传热传质性能得到深入研究，并广泛地应用于诸多微电子设备散热问题的解决[5-8]。

在研究微通道热沉的传热传质性能时，合理地确定微通道固液接触面上的速度边界条件是必须要解决的问题之一。虽然前人就微通道热沉的截面形状和尺寸对于流体阻力及散热性能的影响进行了大量的研究[9-11]，但是，大多数研究考虑的是无边界滑移条件，即在微通道固液接触面上没有相对运动速度。然而，在微纳尺度下的流体流动，无边界滑移并不完全适用。已有的研究发现，边界滑移确实存在于微尺度下的流体流动中[12-13]。相对应于无边界滑移，边界滑移是指在固液接触面上流体分子与固体表面之间有相对运动速度的存在。为表征边界滑移的程度，Navier[14]提出了线性滑移边界条件假设，给出了滑移长度的概念，用于表征边界滑移的程度[14-16]。已有研究发现，滑移长度的范围可在几纳米到几十微米之间[17]，这会对微通道流体的传热传质性能产生显著的影响。

为了解决上述问题，本文选用具有矩形、椭圆形和三角形这3种不同截面形状的微通道热沉，研究了边界滑移对微通道热沉传热传质的影响，以及微通道热沉传热传质性能的截面形状和截面尺寸依赖性问题。

1 微通道仿真模型的建立

微通道散热主要是通过流体与热源进行热量的交换传递，由流体将热量带走。为研究微通道热沉传热传质性能的截面形状依赖性，本文建立了具有3种不同截面形状的微通道热沉模型，截面形状分别为矩形、椭圆和等腰三角形，具体结构如图1所示。同时，在保证截面横截面积不变的条件下，通过调整椭圆截面的长短轴之比、矩形截面的高宽之比和等腰三角形截面的顶角及腰长的方式来调整截面的尺寸，研究微通道热沉传热传质性能的尺寸依赖性。考虑微通道热沉整体结构的对称性，本文仅选用具有单根管道的区域进行仿真，仿真区域如图1中虚线框所示，3种截面形状的截面面积均为225π μm2，仿真区域通道长度 L为 1 000 μm，宽 W和高 H均为 200 μm。a和b分别表示椭圆截面的长轴和短轴，t和w分别表示矩形截面的高和宽，l和θ分别表示等腰三角形截面的腰长和顶角。

假设微通道中的流体为不可压缩牛顿流体且在层流的状态下流动，同时，假定流体处于稳定流状态且忽略重力等体积力的影响。此时，流体的流动状态应满足连续介质理论，并由以下控制方程[18]来描述：

式中：v为流体流动的速度；ρ为流体的密度；p为压力；η为流体的动力黏度。

此外，假定热量传递处于热稳定的状态，热量在微通道热沉中稳定传递的控制方程为[18]：

流体区域

式中：cp为流体的比定压热容；kf为流体的导热系数；T为流体温度；ks为散热器固体导热系数；Ts为散热器固体温度。

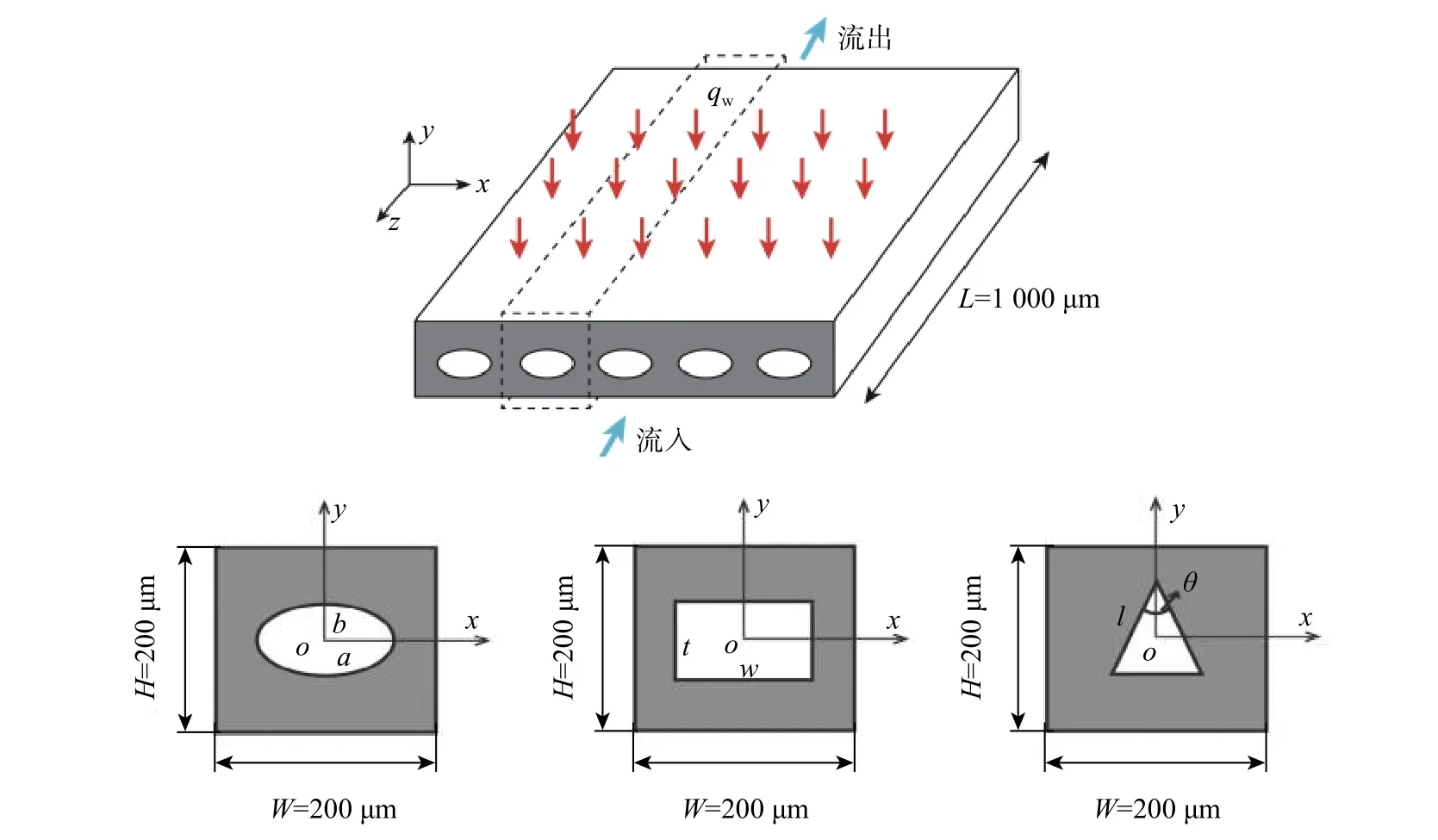
图1 微通道热沉仿真模型Fig.1 Simulation models for microchannel heat sinks

流体流动及传热的初始条件及边界条件为

式中：vin，Tin分别为进口速度与进口温度；pout为流体的出口压力；vfw为固液接触面的相对运动速度；为垂直于管道方向的流体速度梯度；n为垂直于管道壁的局部坐标；vf为液体运动速度；ls为固液界面上的滑移长度。

实际研究通过Comsol软件仿真实现，选用水为冷却液体，微通道热沉的材料为硅。微通道热沉的上表面有105W/m2的热流量，热沉其他几个面为热绝缘边界，入口处水的速度为5 m/s，温度为293.15 K，固体的导热系数ks=130 W/（m·K），水的导热系数 kf=0.6 W/（m·K），水的密度 ρ=996.6 kg/m3，水的比定压热容 cp=4 178 J/（kg·K），水的动力黏度η=0.001 Pa·s，且忽略温度变化对水的物性参数的影响。为了研究滑移的影响，假定固液接触面上具有不同的滑移长度（0～1 000 nm），对此进行仿真分析。

此外，引入流体阻力R及传热系数h这2个参数来分析微通道热沉的传热传质性能。根据泊肃叶定律可知，流体在水平通道中作无滑移层流运动时，其体积流量Q与管道两端的压差Δp，管的水力半径r，长度L，以及流体的动力黏度η的关系为[19]

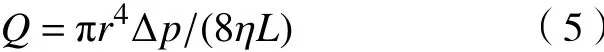
令 R=Δp/Q =8ηL/(πr4)，R 即为圆管流体阻力的计算公式。Comsol仿真研究的R可由式（6）直接计算得出。

其中，Δp，Q由Comsol仿真结果得出。

当有边界滑移存在时，流体阻力可表示为[20]

泊肃叶定律是建立在流体在水平圆管中作层流运动时，当流体在任意截面形状的微通道中作层流运动时，通道的水力半径可通过式r=2A/P得出，A为微通道截面面积，P为截面周长。

根据牛顿冷却定律可知，流体与固体壁面之间的对流传热的热流量与它们之间的温度差成正比，可以表示为

式中；Qh为单位时间内面积Asl（微通道中固液接触面积）上传热的热流量；Tb表示微通道壁面温度；Tw表示微通道中水的平均温度。

Qh可以表示为

式中：c表示流体的比热容；q为质量流量；Twi表示微通道入口处水的温度；Two表示微通道出口处水的温度。

2 结果与讨论

2.1 仿真模型有效性分析

在Comsol仿真分析过程中，为保证模型的正确性以及网格划分的准确性，需要对仿真模型进行验证及网格灵敏性分析。采用的具体分析方法是以截面半径为15 μm，通道长度为1 000 μm的圆形微通道为例，通过调整网格尺寸，将Comsol仿真得到的具有不同边界滑移长度的微圆管流阻与式（7）的理论模型进行比较。当Comsol仿真结果与理论模型的误差足够小时，说明模型网格划分合理，仿真模型是正确的。分析发现，当采用自由四面体网格，且网格数量为2.73×105时，可以得到较为准确的仿真结果。如图2所示，仿真分析与理论结果之间的最大误差仅为2.5%（滑移长度为1 μm时），图中R0为无滑移时的流体阻力，ls为滑移长度。类似地，每一组模型都采用相同的方法进行了有效性分析，保证网格划分是合理的。

2.2 滑移长度对流体阻力和传热系数的影响

为了分析边界滑移对流体阻力的影响，图3给出了边界滑移条件对3组不同截面形状微通道热沉内的流体阻力影响的分析结果。R01表示截面尺寸为26.6 μm×26.6 μm的矩形微通道热沉无滑移时的流体阻力，R02表示截面尺寸为 15 μm×15 μm的圆形微通道热沉无滑移时的流体阻力，R03表示截面尺寸为 40.4 μm×60 ° 的三角形微通道热沉无滑移时的流体阻力。图3结果表明，边界滑移的存在减弱了流体阻力，并且随着滑移长度的增加，流体阻力逐渐减小。这与式（7）给出的流体阻力的理论结果一致。其原因是由于边界滑移的存在影响了微通道流体的流动速度，流体流动速度随边界滑移的增大而增加。所以，在相同的驱动压力下，边界滑移增强了流体的流动，导致了体积流量的增加，意味着流体阻力的减小。

图2 理论分析与仿真分析结果对比Fig.2 Comparison between the results of theoretical analysis and simulation analysis

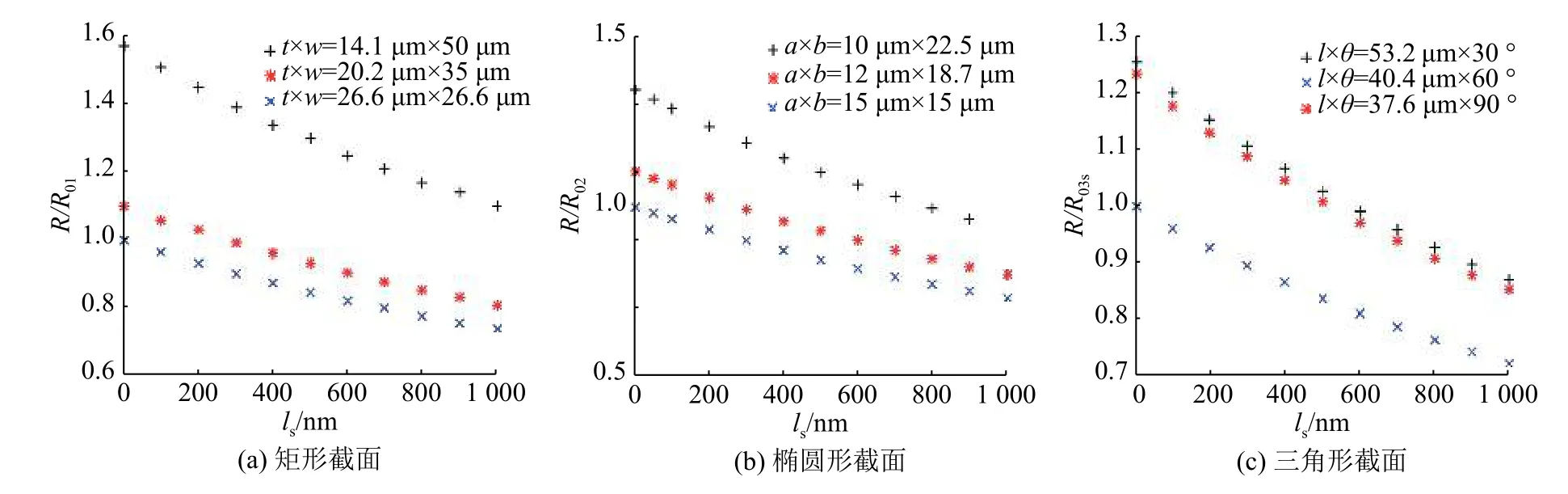
图3 滑移长度对矩形、椭圆形和三角形微通道流体阻力的影响Fig.3 Effect of slip length on the fluid resistance in rectangular, triangular and elliptical microchannels

图4 给出了在相同的截面面积条件下，具有不同截面形状及尺寸的微通道热沉中边界滑移对传热系数影响的结果，h01表示截面尺寸为26.6 μm×26.6 μm的矩形微通道热沉无滑移时传热系数，h02表示截面尺寸为15 μm×15 μm的圆形微通道热沉无滑移时传热系数，h03表示截面尺寸为40.4 μm×60 ° 的三角形微通道热沉无滑移时传热系数。由图4可以看出，边界滑移可以有效地提高微通道热沉的对流换热性能，而且传热系数随着滑移长度的增加而增加。这是因为在相同的驱动压力下，边界滑移导致流体流速的增加，从而导致体积流量的增加，单位时间内微通道中流过更多的流体，带走更多的热量，导致散热能力的增强以及传热系数的增加。

图4 滑移长度对矩形、椭圆形和三角形微通道传热系数的影响Fig.4 Effect of slip length on the heat transfer coefficient of rectangular, elliptical and triangular microchannels

2.3 截面尺寸对流体阻力及传热系数的影响

为了研究截面尺寸对流体阻力的影响，图5给出了在相同截面面积下，具有不同截面形状的微通道热沉截面尺寸对流体阻力影响的结果。由图5可知，在固液界面上具有相同滑移长度的条件下，矩形微通道热沉内的流体阻力随着矩形截面高宽比值（t/w）的增加呈现先减后增的趋势；当矩形截面高宽比为1，即截面为正方形时，微通道热沉具有最小的流体阻力。对于椭圆形微通道热沉，流体阻力随着椭圆截面2个半轴比值（a/b）的增加，呈现先减后增的趋势；当椭圆截面2个半轴比值（a/b）为1，即截面为圆形时，微通道热沉具有最小的流体阻力。对等腰三角形截面，随着顶角由15 ° 增至135 °，流体阻力先减后增；当顶角为60 °，即截面为等边三角形时，微通道热沉具有最小的流体阻力。图5中的结果可以根据式（7）中水力直径对流体阻力的影响进行解释。已知随着水力直径D的增加，流体阻力逐渐减小。对于图5中的结果，随着矩形高宽比（t/w）和椭圆2个半轴比值（a/b）的增加，微通道的水力直径先增后减；当t/w=1或a/b=1时，相应的微通道水力直径最大。而随着等腰三角形顶角向60 ° 靠近，三角形截面的水力直径逐渐增大，当顶角为60 ° 时，三角形截面的水力直径最大。由式（7）可知，随着水力直径的增加，流体阻力逐渐减小，进而得到图5所示的结果。

图6给出了相同截面面积条件下，具有不同截面形状的微通道热沉截面尺寸对对流传热系数影响的结果。图6的结果表明，在相同滑移长度下，传热系数随着矩形高宽比的增加而先减后增；当矩形高宽比为1时，传热系数最小，即微通道热沉具有最差的散热能力。类似地，当椭圆形2个半轴之比（a/b）为1时，传热系数达到最小，并且传热系数随着椭圆长短轴比值的增加而增加。对等腰三角形截面，当顶角为60 °，即为等边三角形时，传热系数最低，散热能力最弱；当顶角从15 °增加到135 ° 过程中，传热系数先减后增。上述结果也可由微通道水力直径的变化来解释。相同的截面面积下，具有较小水力直径的微通道热沉有着较大的固液接触面积，有助于传递给流体更多的热量，并由流体带走，故具有较大的对流传热系数。

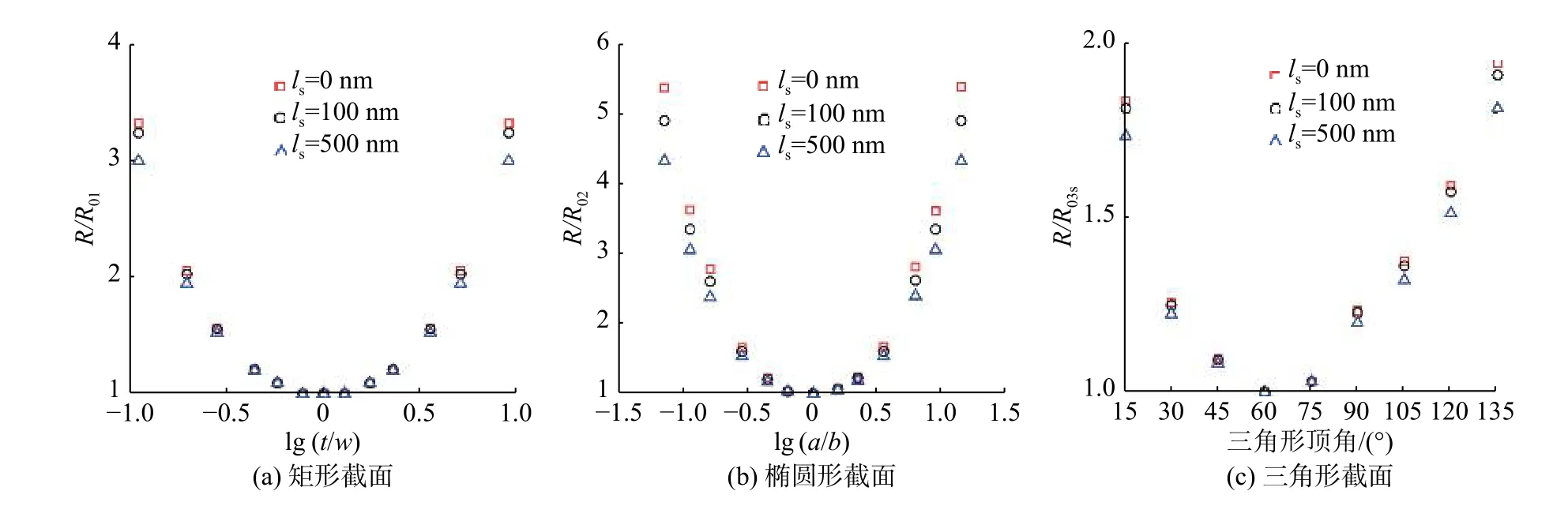
图5 截面尺寸对矩形、椭圆形和三角形微通道流体阻力的影响Fig.5 Effect of cross-sectional dimensions on the fluid resistance in rectangular, elliptical and triangular microchannels

2.4 截面形状对传热系数的影响

图7 给出了不同截面形状对微通道热沉散热性能影响的结果。图7表明，3种截面形状的微通道热沉的散热性能都是随着水力直径的增加而减弱，这与图6所示的结果一致。同时，三角形微通道热沉的散热性能在这三者中是最差的。对于矩形和椭圆形微通道热沉，当水力直径小于某一临界值时，矩形截面微通道热沉的散热性能优于椭圆形微通道热沉，但当水力直径大于这一临界值时，椭圆形微通道热沉的散热效果好于矩形微通道热沉。

图6 截面尺寸对矩形、椭圆形和三角形微通道传热系数的影响Fig.6 Effect of cross-sectional dimensions on the heat transfer coefficients of rectangular, elliptical and triangular microchannels

图7 水力直径对无滑移和有滑移条件下具有不同截面形状微通道传热系数的影响Fig.7 Influence of hydraulic diameter on the heat transfer coefficient of microchannels with different cross-sectional shapes

3 结 论

对具有矩形、椭圆和三角形这3种不同微通道截面形状的微通道热沉的传热传质性能进行了研究，得出结论：

a. 当固液界面存在边界滑移时，微通道热沉内的流体阻力随着滑移长度的增加而减小，传热系数随着滑移长度的增加而增大。所以，边界滑移有助于降低流阻，增强散热性能。

b. 在相同截面面积条件下，通过调整矩形截面的高宽比、椭圆截面的长短轴之比和等腰三角形截面的顶角及腰长的方式来改变截面尺寸，发现流体阻力随着水力直径的增加而减小，传热系数随着水力直径的增加而减小。相同截面形状条件下，正方形、圆形和等边三角形微通道热沉具有最小的流体阻力和最差的散热性能。

c. 在相同截面面积条件下，对于具有矩形、椭圆和等腰三角形这3种不同截面形状的微通道热沉，三角形微通道热沉的散热性能在这三者中最弱；对于矩形和椭圆形微通道热沉，存在某一临界值使得水力直径小于这一临界值时，矩形微通道热沉的散热性能优于椭圆形微通道热沉，当水力直径大于这一临界值时，椭圆形微通道热沉的散热能力大于矩形微通道热沉。

研究表明，引入边界滑移并合理调整微通道截面形状和尺寸可以优化微通道热沉的传热传质性能，这为微通道热沉的优化设计提供了一定的借鉴。此外，本文研究可以进一步采用实验进行验证，利用微量泵驱动流体在微通道热沉内流动，并通过加热装置模拟发热元件，将热沉置于其上以模拟整个散热过程。利用温度传感器、压力传感器等对实验过程中的关键数据进行测量，并进一步分析得到系统的流阻和热阻。实验中应严格控制变量，保证微通道横截面积保持不变，改变截面形状、尺寸和滑移条件，对于滑移长度的调整可以通过改变管道内表面的粗糙度、溶液的pH等方式实现。