基于SCE-PSO的无线传感器网络节点三维定位方法*

刘 伟,李 卓,杨晓斐,杨丽燕

(1.桂林理工大学信息科学与工程学院,桂林 541006,;2.桂林理工大学广西嵌入式技术与智能系统重点实验室,桂林 541006)

无线传感器网络是一种由大量结构简单、廉价的传感器集成无线通信接口所组成的网络,它在环境监测、灾难救助、目标跟踪等领域都有广泛的应用前景。在这些应用中,传感器节点的自我定位非常重要,因为没有和具体的坐标联系在一起的监测信息通常是没有意义的。同时,如基于地理信息的路由等无线传感器网络协议也需要节点的位置信息作为支撑。因此节点定位问题是无线传感器网络的重要研究内容之一[1-3]。

根据是否需要测量节点之间的距离,无线传感器网络的节点定位方法可以划分为基于测距和基于非测距的两种方法。其中基于测距的方法,由于定位精度高在无线传感器网络节点定位中被广泛采用。基于测距的定位方法首先要测量节点之间的距离或角度。常用的测量方法有接收信号强度指示RSSI(Received Signal Strength Indicator)[4-5]、到达时间TOA(Time of Arrival)[6-7]、到达时间不同TDOA(Time Difference of Arrival)[8-9]和到达角度AOA(Angle of Arrival)[10-11]。在获得距离或角度信息以后,基于测距的方法即可以采用各种方法对未知节点进行定位。

目前对无线传感器网络节点定位的研究主要集中在二维空间,而在实际应用中,传感器节点通常分布在三维空间内,需要节点的三维空间信息,如海洋、山地、森林及各种空间飞行器等。因此非常有必要研究无线传感器网络节点的三维节点定位方法。

获取节点之间的距离或角度信息后,基于测距的方法就可以采用一些定位方法对未知节点进行定位,其中一类方法是把获取的距离或角度信息看作约束条件,将其转化为一个目标函数,然后用各种优化算法寻找该目标函数的最小值,从而对未知节点进行定位。优化方法可分为传统的优化方法和生物启发式优化方法。

传统的优化方法基于确定的搜索策略,在满足一定的限制条件下,利用优化问题的导数、梯度等数学性质进行求解。该类方法的缺点是运算复杂度较高,并且随着问题的维数的增大其复杂度以指数倍增加,生物启发式优化方法可以有效地避免这个问题,使计算更加有效,对优化问题所对应的函数形式不做任何假设,而且不要求目标函数的连续性或可导性的假设,算法简单,易于实现。

常见的生物启发式优化算法包括:模拟退火算法SA(Simulated Annealing)[12-13]、蚁群算法ACO(Ant Colony Optimization)[14]、遗传算法GA(Genetic Algorithm)[15-16]、人工蜂群算法ABC(Artificial Bee Colony)[17]、细菌觅食算法BFA(Bacterial Foraging Algorithm)[18]、粒子群算法PSO(Particle Swarm Optimization)[18-20]。与其他生物启发式优化算法相比,粒子群算法具有容易执行,收敛速度比较快的优点。尤其是求解的问题维数越多,其优势越明显[18]。因此,粒子群算法非常适用于无线传感器网络节点的三维定位。但是,在运行过程中,粒子群算法可能会陷入局部最优,出现早熟收敛现象。避免粒子群算法出现早熟收敛现象的措施之一是增加粒子的多样性,而SCE-UA(Shuffling Complex Evolution-University of Arizona)算法中的洗牌策略可以很好地保持粒子的多样性,因此,为了克服粒子群算法的这一缺点,我们结合SCE-UA(Shuffling Complex Evolution-University of Arizona)算法,提出了两种基于SCE-PSO的无线传感器网络节点三维定位方法。

本文剩余部分安排如下:第一节简单介绍一下粒子群算法和SCE-UA算法;第二节详细介绍我们提出的两种基于SCE-PSO的无线传感器网络节点三维定位方法;第三节为仿真分析;最后一节对本文作出总结。

1 粒子群算法和SCE-UA算法概述

1.1 粒子群算法

粒子群优化算法是1995年由Kennedy和Eberhart共同提出的,其起源于人们对鸟群等群居性动物觅食行为的研究[21]。粒子群优化算法的基本思想是:将优化问题的每一个解看作一个微粒,每个微粒在多维搜索空间中以一定的速度飞行,通过目标函数的适应度值衡量微粒的优劣,每个微粒能够通过自己的飞行经验以及其他微粒的飞行经验,动态地调整自己的飞行速度,从而向群体中最好的微粒位置飞行,最终搜索到优化问题的最优解。

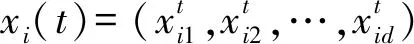
xi(t+1)=xi(t)+vi(t+1)

(1)

vi(t+1)=w·vi(t)+c1r1[pi-xi(t)]+c2r2[g-xi(t)]

(2)

式中:pi是第i个粒子自己所找到的最优解,g是整个总群所找到的最优解,w是惯性权重,c1和c2是学习因子,一般选取c1=c2=2;r1和r2是在(0,1)区间上服从均匀分布的随机数。

为了防止粒子远离搜索空间,粒子的飞行速度v都被限制在[-vmax,vmax]之间。vmax较大,可以保证粒子种群的全局搜索能力;vmax较小,则粒子种群的局部搜索能力加强。

1.2 SCE-UA算法

SCE-UA算法是由美国亚利桑那州大学的Qingyun Duan博士在1992年提出的,它是一种有效的解决非线性约束最优化问题的方法[22]。目前其主要运用在流域水文模型的参数优选。SCE-UA算法基本思路是将基于确定性的复合形搜索技术和自然界中生物竞争进化原理相结合,用来求解最小化问题,融合了确定性方法、随机性方法、竞争进化、复合形混合等概念,从而保证了SCE-UA算法搜索的灵活性、全局性、一致性和有效性等。SCE-UA算法的最要步骤如下:

①初始化。假定待优化的问题是n维问题,选取参与进化的复合形个数p(p≥1)和每个复合形所包含的顶点数目m(m≥n+1),并计算样本点数目s=p×m。

②产生样本点。在可行域内随机产生s个样本点x1,x2,…,xs,分别计算每一个点xi的函数值fi=f(xi),i=1,2,…,s。

③样本点排序。把s个样本点(xi,fi)按照函数值的升序排列,排序后仍记为(xi,fi),i=1,2,…,s,也就是f1≤f2≤…≤fs,记D={(xi,fi),i=1,2,…,s}。

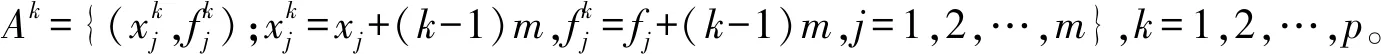
⑤复合形进化。按照下山单纯形算法分别进化每一个复合形。

⑥复合形混合。把进化后的每个复合形的所有顶点组合成新的点集,再次按函数值fi的升序排列,排序后仍记为D,对D按目标函数的升序进行排列。

⑦收敛性判断。如果满足收敛条件则停止迭代,否则回到第④步。

SCE-UA算法的参数虽然较多,但绝大部分取值都可以采用已有研究成果的默认值,只有复合形个数p需要根据具体问题确定。根据文献[22]推荐m=2n+1,q=n+1,s=p×m,α=1,β=2n+1。其中n为参数的个数,m为每个复合形顶点的个数,q为每个子复合形的顶点数,s为种群大小,α和β为下山单纯形算法中父代产生的子代的个数及代数。

2 基于SCE-PSO的无线传感器网络节点三维定位方法

2.1 无线传感器网络节点的三维定位目标函数

假设在三维空间中,无线传感器网络中的未知节点的坐标是(x,y,z),锚节点的坐标分别为(x1,y1,z1),(x2,y2,z2),…,(xn,yn,zn),未知节点到锚节点的距离分别为d1,d2,…,dn。由此,我们可以得出如下的式(3)。

(3)

因此,无线传感器网络节点三维定位的目标函数可以定义为:

(4)

2.2 基于SCE-PSO的优化算法

粒子群优化算法中的速度更新式(2)有三部分组成,第一部分是粒子先前的速度,说明了粒子目前的状态,具有平衡全局和局部搜索的能力;第二部分是认知部分,表示粒子本身的思考,使粒子具有足够强的全局搜索能力,避免局部极小;第三部分为社会部分,体现了粒子间的信息共享,这使得PSO能够迅速找到最优解。

粒子群算法在运行的过程中,如果某一个粒子发现一个当前最优位置,其他粒子将迅速向其靠近,如果该最优位置只是一个局部最优点,粒子群在搜索的过程中可能无法跳出这个局部最优点,因此会陷入局部最优,出现早熟收敛现象。避免粒子群算法出现早熟收敛现象的措施之一是增加粒子的多样性。在此我们借鉴SCE-UA算法,提出了两个基于SCE-PSO的优化方法SCE-PSO1和SCE-PSO2。

在传统的SCE-UA算法中,采用的是下山单纯形算法进化每一个复合形。但是下山单纯形算法是用多面体来逐步逼近问题的最佳值。如果待优化问题的维数比较大,其进化过程就显得比较复杂,所求出的解得质量也不高,而且收敛速度也相对缓慢。由于无线传感器网络节点三维定位的维数较大,因此不适合用该方法进行定位。而粒子群算法没有选择、交叉、变异等操作,其收敛速度较快,而且收敛速度受优化问题维数的影响也比较小,因此比较适用于无线传感器网络节点的三维定位。

鉴于上述思想,我们提出了SCE-PSO1算法。在该算法中,我们用粒子群算法代替下山单纯形算法去进化SCE-UA算法中每一个复合形。这样可以克服传统SCE-UA算法的缺点,提高收敛速度,增加求解高维数问题的解的质量;同时也可以利用SCE-UA算法中的洗牌策略(复合形混合之后,再重新划分)保持粒子的多样性,从而克服粒子群算法的缺点,减少其出现早熟收敛的概率。

在SCE-PSO1算法中,采用粒子群算法进化每一个复合形。每一个复合形在进化过程中,其粒子的速度用式(2)更新。在式(2)中,pi是第i个粒子自己所找到的最优解,g是该复合形中的粒子所找到的最优解。因此式(2)并没有体现进化过程中各个复合形之间信息的共享。为了加快收敛速度,提高解的质量,我们提出了SCE-PSO2算法。在SCE-PSO2算法中,每一个复合形在进化过程中,其粒子的速度不再使用式(2)更新,而是用下面的式(5)进行更新。

vi(t+1)=w·vi(t)+c1·r1[pi-xi(t)]+
c2·r2[g-xi(t)]+c3·r3[e-xi(t)]

(5)

在式(5)中,pi是复合形中第i个粒子本身找到的最优解,g是该复合形中的粒子找到的最优解,e是所有复合形中的粒子找到的最优解。w是惯性权重,c1、c2和c3是学习因子,r1、r2和r3是在(0,1)区间上服从均匀分布的随机数。式(5)包含四个部分,其中前三个部分与式(2)相同,第四部分表示进化过程中各个复合形之间信息的共享。

3 仿真分析

为了验证我们提出的SCE-PSO1和SCE-PSO2算法的性能,我们选取PSO和SCE-UA算法与其作对比,并使用MATLAB R2013a软件进行仿真。我们在边长为100 m的立方体网络区域中放置了125个节点,节点的分布为均匀分布,节点间距离是20 m(存在0～2 m的随机误差)。

为了保证算法可比性,4种算法的群体规模均取为14,PSO、SCE-PSO1和SCE-PSO2算法中的惯性权重w采用自适应调整策略:w=wmax-t(wmax-wmin)/T,其中t指当前的迭代次数,T指最大的迭代次数,T=20;wmax=0.9;wmin=0.4。PSO和SCE-PSO1算法中粒子的最大飞行速度wmax=20.tif;SCE-PSO2算法中粒子的最大飞行速度wmax=50.tif;SCE-UA算法中复合形的个数p=2,其余参数按照文献[22]的推荐选取,即问题的维数n=3,每个复合形顶点的个数m=7;下山单纯形算法中每个子复合形的顶点数q=4;父代产生的子代个数α=1;产生的子代的代数β=7。

我们仿真了不同锚节点数量、不同通信半径和不同测距误差下,上述4种方法的平均定位误差。平均定位误差采用下式计算:

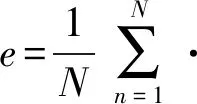
(6)

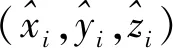
3.1 不同锚节点数量的仿真对比

本次仿真节点的通信半径为50 m,测距误差为均值为0,标准差为4的高斯噪声。仿真结果如图1所示。

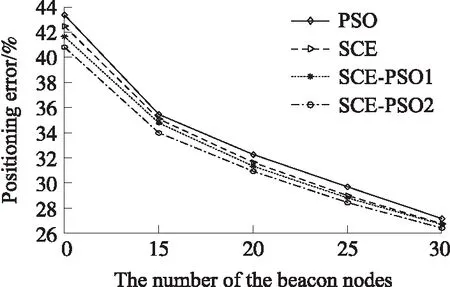
图1 不同锚节点数量的仿真性能

从图1中可以看出,随着锚节点数量的增大,4种优化算法的平均定位误差逐渐降低。这是由于节点总数与通信半径一定时,锚节点越多,参与未知节点定位的锚节点越多,节点的定位信息越丰富。从图1中还可以看出,SCE-PSO2算法的性能是最好的,其次是SCE-PSO1算法,而PSO算法的性能最差。

3.2 不同通信半径的仿真对比

本次仿真锚节点的数量为15,测距误差为均值为0,标准差为4的高斯噪声。仿真结果如图2所示。

从图2中可以看出,随着通信半径的增大,4种优化算法的平均定位误差逐渐降低。这是由于节点总数与锚节点数量一定时,通信半径越大,参与未知节点定位的锚节点越多,节点的定位信息越丰富。从图1中还可以看出,SCE-PSO2算法的性能是最好的,其次是SCE-PSO1算法,而PSO算法的性能最差。

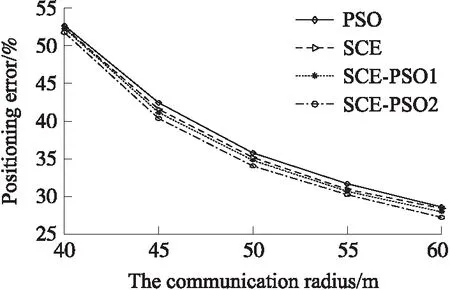
图2 不同通信半径的仿真性能

3.3 不同测距误差的仿真对比

本次仿真锚节点的数量为15,节点的通信半径为50 m,测距误差为均值为0的高斯噪声。我们仿真了不同仿真噪声标准差下,4种优化算法的平均定位误差,仿真结果如图3所示。

从图3中可以看出,随着测距误差的增大,4种优化算法的平均定位误差逐渐增加。这是由于测距误差越大,测量距离与真实距离的偏差越大,因此节点的定位越不准确。从图3中还可以看出,SCE-PSO2算法的性能是最好的,其次是SCE-PSO1算法,而PSO算法的性能最差。

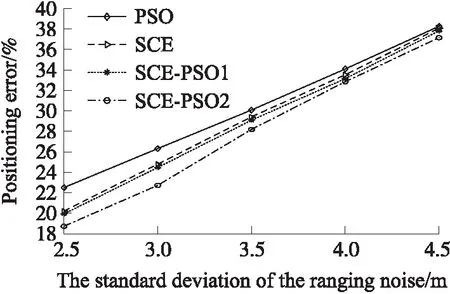
图3 不同测距误差的仿真性能

综合上面的三个仿真结果,可以看出,我们提出的SCE-PSO1和SCE-PSO2算法的性能均优于原始的PSO和SCE算法,而且SCE-PSO2算法的性能要优于SCE-PSO1算法。这是因为与原始PSO算法相比,在SCE-PSO1和SCE-PSO2算法中,我们引入了洗牌策略,增加了粒子的多样性,从而减少了PSO算法出现早熟收敛的概率;而与原始SCE算法相比,在SCE-PSO1和SCE-PSO2算法中,我们用PSO算法取代受维数影响较大的下山单纯形算法去进化每个复合形,从而提高了搜索速度和解的质量。而与SCE-PSO1算法相比,在SCE-PSO2算法中,我们在粒子的更新速度式(5)中,引入了各个复合形之间信息的共享,从而进一步提高了搜索速度和解的质量。

4 结论

本文提出了SCE-PSO1和SCE-PSO2两种无线传感器网络节点三维定位方法,其综合了PSO和SCE两种优化方法的优点,减轻了PSO方法中粒子早熟收敛的现象,同时改善了SCE-UA方法受问题维数影响较大的缺点,因此,SCE-PSO1和SCE-PSO2方法非常适用于无线传感器网络节点的三维定位。仿真结果证明,SCE-PSO1和SCE-PSO2两种方法的性能均优于原始的PSO和SCE两种方法,而且由于在SCE-PSO2中增加了各个复合形之间信息的共享,其性能要优于SCE-PSO1方法。