基于可信度的地磁与惯导联合室内定位系统*

余刘勇,单志龙

(华南师范大学计算机学院,广州 510631)

随着智能手机和移动互联网的发展,人们的衣食住行方式发生了翻天覆地的变化。人们出行方式的改变,促进了定位信息的需求量增加,大力发展移动定位技术变得尤为重要。传统的卫星定位技术仅仅局限于室外,室内移动物体的定位不能依赖该技术,必须通过其他定位技术来获取位置信息[1]。因此,通过充分挖掘室内定位确定性信息和进行室内定位技术研究具有较大的实际应用价值。

早期地磁研究主要适用在宽阔的野外,通过对地磁信息的研究来绘制地磁分布图。近些年,建筑物内地磁信息分布的研究不断被提及,得益于建筑物的长期不变性,在室内的地磁异常信息具有一定的稳定性,地磁定位就是利用这些异常信息产生的稳定磁场作为信标来进行定位[2]。目前,国内外对地磁的研究取得了一定的进展,但大部分研究还局限在匹配算法和模拟仿真方向,对于真实室内环境地磁信息的检测、异常处理和定位系统实用性方面研究还比较欠缺。宋镖[3]等人提出了惯导辅助地磁的手机室内定位系统,降低了地磁检测和匹配时间,定位精度达到了1 m左右。但并未充分使用惯导的确定性信息来降低地磁匹配产生的误差,且离线指纹库需要划分网格进行采集,耗时耗力;杨增瑞[4]等人提出了地磁指纹辅助的手机室内定位系统,通过一种新的思路进行行人航位推算,实现了2 m左右的定位精度;李思民[5]等人提出了地磁指纹和PDR(Pedestrian Dead Reckoning)融合的手机室内定位系统,利用PDR定位结果缩小地磁匹配区域,实现了2 m左右的定位精度;谢宏伟[6]等人提出了一种基于稳定性增强粒子滤波磁场匹配算法的手机室内定位系统,达到了1 m～2 m左右的精度,但实现算法过于复杂,计算速度慢;Haverinen[7]等人提出了基于粒子滤波的室内定位系统,该系统对用户的行走有严格的要求,实用性不强。通过分析发现,现有室内地磁定位方法往往需要耗费大量的时间进行数据采集与计算,且无法充分挖掘定位阶段的确定性信息,这些因素都阻碍了室内定位技术的发展和应用。

传统地磁定位单纯的采集地磁指纹信息进行地磁匹配并获得节点位置,其中地磁匹配主要是计算实测值与基准库指纹数值的相似程度,主要的算法有最小距离度量法、相关度量法[8]和粒子滤波[6]。最小距离度量法主要有绝对差法(Absolute Difference,AD)、平均绝对差法MAD(Mean Absolute Difference)、平方差法SD(Square Difference)和平均平方差法MSD(Mean Square Difference);相关度量法主要有积相关法PROD(Product Correlation Similarity Measure)和归一化积相关法NPROD(Normalized Product Correlation Similarity Measure);粒子滤波是根据蒙特卡罗思想,通过以样本均值代替积分运算,进而获得系统状态的最小方差估计的过程。其中,粒子滤波具有较好的算法精度且在各种领域都广泛使用,但其实现过程较为复杂,计算量大。MAD和MSD的算法精度较高,计算复杂度低,计算量小。

本文提出了一种基于可信度的地磁与惯导联合定位方法GINPC(Geomagnetic and Inertial Navigation Positioning Based on Credibility),并采用该方法设计了一套完整的室内定位系统。该方法以路径段为单位,使用惯导技术进行地磁数据的快速采集处理,充分挖掘地磁与惯导信息的确定性因素,最终估算出节点位置。该方法可以有效的减少前期构建基准库耗费的大量人力和时间,并在定位阶段减少地磁匹配的次数,降低系统的复杂度。

1 GINPC定位系统

不同的定位方法都有其各自优势,但也存在各自的局限。地磁指纹定位具有较高的可扩展性和定位精度[9],但存在较大的随机误差,不能很好的保证估计位置的准确性,所以现今研究中大多采用地磁信息与其他多种信息融合的方式来进行室内定位。GINPC定位系统就是采用地磁与惯导信息联合实现室内的行人位置估计,包含离线和在线[10]两个阶段,如图1所示,GINPC定位系统在离线阶段先通过惯导技术计算出坐标,然后将对应坐标中的地磁数据录入惯导地磁基准库中;在线阶段,通过路径匹配和地磁匹配获得的可信度进行联合定位并最终获得估计位置。

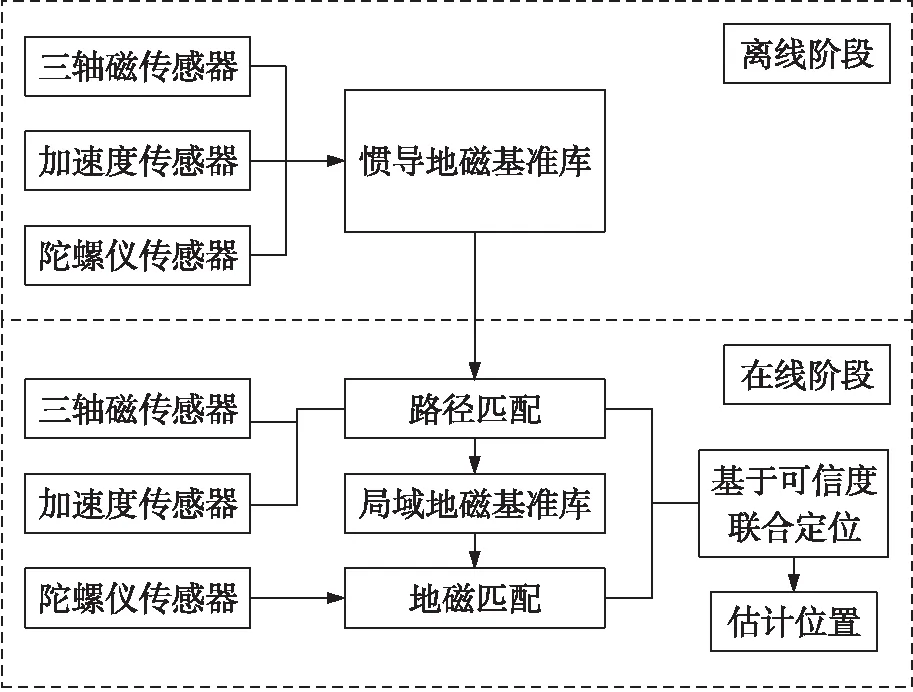
图1 GINPC定位系统框图

1.1 离线阶段

在离线阶段,事先不需要进行场景的网格划分,只需以路径段为单位,采集人员按预先设定的路径匀速行走,利用智能手机上的三轴磁传感器、加速度传感器和陀螺仪传感器,采用惯导技术实时计算出采集人员行走的位置,并通过地磁采集系统记录采集人员所在位置的地磁指纹信息,建立基于路径段的惯导地磁基准库。

为保证惯导信息的有效性,本算法通过步频检测、步长估计和方位角估计进行惯导信息的获取。

1.1.1 步频检测

行人行走时的步态信息可利用手机的加速度传感器进行探测,随着行人的行走,加速度会呈现一定的周期性,因此通过分析加速度波形可以得到较为准确的步频信息,如图2所示。步频检测目前常用的方法是过零点峰值检测法[11],通过零点和峰值的阈值设置来判断行人是否走步。考虑到系统复杂度,本方法将采用过零点峰值检测法来进行步频检测。

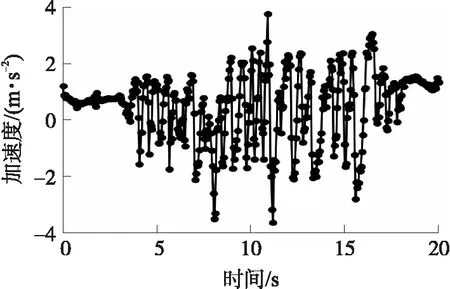
图2 手机加速度数据分布图

在过零点峰值检测法中,加速度ai被称为上升过零点,若加速度ai满足:

(1)

式中:i为上升过零点的采样序号。

行人行走姿态的多样性和传感器的误差会使加速度数据波形产生毛刺,所以可先将采样数据通过低通滤波器进行滤波处理,然后再检测上升过零点。前后两个相邻的上升过零点之间的时间差即为一个完整的步态周期。为了防止单个周期内出现多个波形峰值,只有当一次检测的加速度峰值大于某一个阈值时,才判定为一步的完成,即:

a′>a0

(2)

式中:a′为检测到的加速度峰值,a0为峰值检测阈值。

1.1.2 步长估计

在进行惯导计算时,建立精准的行人步长估计模型十分重要[12]。行人步长与步频和加速度有关,由文献12可知,随着加速度、步频的变化,步长呈正相关变化。因此,可以建立步长与步频和加速度的线性关系方程。

L=Aa+BF+C

(3)

式中:A,B,C为模型参数,a为行走合加速度,F为行走步频,C为补偿参数。该模型计算复杂度低,可以反映步长的随机变化,通过对不同人的测试训练可的得到较为准确的步长值。

1.1.3 方位角估计

方位角一般由磁力计和陀螺仪数值计算得出,因为电子设备容易受到干扰,行人行走过程中的抖动和陀螺仪的漂移都会导致方位角误差。因此,将磁力计和陀螺仪相结合,使用互补滤波器处理两者信号,最终可以得到行人方位角[13-14]。

如图3所示,通过低通滤波器滤除磁力计信号噪声,然后通过磁力信号和陀螺仪信号加权得到行人的方位角θ。

θ=αθr+(1-α)θab

(4)

式中:θr是手机相对地球北极方向夹角;θab为陀螺仪绝对角度;α=Δt/(Δt+Tf)补偿参数,Tf为低通滤波器滤波时间;Δt为手机信号采样时间间隔。

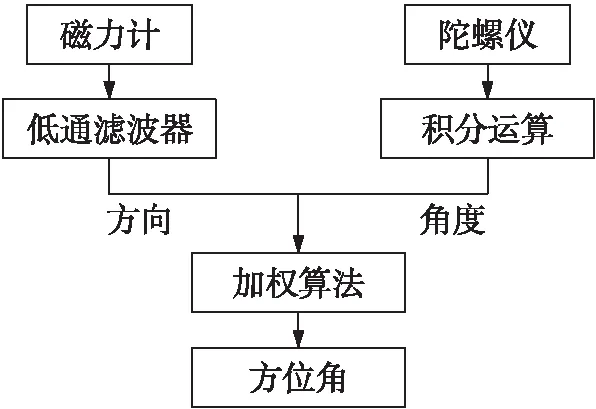
图3 互补滤波器原理

1.1.4 构建惯导地磁基准库

由于地磁信息会随着手机姿态的不同而导致数值不同,如果直接使用手机获得的数值构建基准库,将产生较大的误差。通过相关研究可知[15],地磁信息可以通过标准转换公式进行转换。本文根据航天器的姿态转换模型为基础,将手机测得地磁数值转换到标准坐标轴。

惯导地磁基准库以路径段为单位进行划分,每个路径段进行标记。路径段中每个位置点为P(li,x,y,Ux,Uy,Uz,D,T),其中,li为路径段标号,x,y为利用惯导信息获得的位置坐标,Ux,Uy,Uz为地磁三轴信息转换后的标准数值,D为位置点获取的方位角,T为生成位置点指纹的时间,如表1所示。

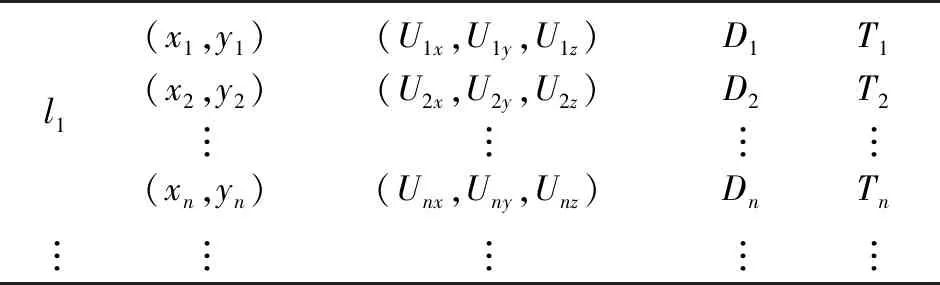
表1 惯导地磁基准库

1.2 在线定位阶段

在线定位算法主要是充分挖掘定位时的确定性信息,然后将确定性信息转化为位置估计的可信度,通过计算得出可信度最高的位置点作为未知节点的坐标,主要分为路径匹配、局域地磁基准库生成、地磁匹配和可信度计算四个步骤。

1.2.1 路径匹配

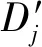
(5)

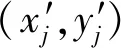
(6)

③位置点距离比较。假设WD为方向比较权重,WL为坐标比较权重,则位置点之间的计算距离为:

(7)

④计算距离标准化。将计算距离标准化为0到1之间的数,得到未知节点与基准库位置点的相似度:

(8)

1.2.2 局域地磁基准库生成

为减少计算量,消除由于地磁波动导致的数值误差,在求得路径点相似度集合后,通过实际路径l′对基准库中的n个惯导路径段l1,l2,l3,…,li,…,ln进行路径的相似度计算,根据相似度对路径进行聚类,再根据聚类结果在惯导地磁基准库中筛选出相似度最高的若干个路径构成局域地磁基准库。

①将实测路径中位置点与基准库中位置点相似度累加,得出实测路径与基准库路径的计算距离:

(9)

②计算距离标准化,将计算距离标准化为0到1之间的数,得到路径相似度:

(10)

③采用ε-近邻集[16]法进行路径段的快速聚类。

ε-近邻集:给定近邻阈值,对于轨迹段li,如果存在轨迹段(lj)(i≠j),满足SSIM(li,lj)≤ε,则称lj属于li的ε-近邻集。使用ε-近邻集聚类方法,获得相似路径集合,生成局域地磁基准库。

1.2.3 地磁匹配

利用平均平方差法(MSD)[8],对局域地磁基准库中的地磁进行匹配,则地磁匹配相关函数D(u,v)为:

(11)

式中:Nuv表示基准图中位置(u,v)上的N维特征向量;m表示实时测量的N维特征向量;N表示相关数据的总点数;Nuv+i表示基准数据库的位置(u,v+i)上的特征量,mi表示实时测量的第i个特征量。

根据MSD计算出未知节点与基准库中节点的平均平方差,假设总共有k个点,通过标准化操作,将结果转换为0-1之间的数:

(12)

1.2.4 可信度计算

惯导信息的可信度由路径匹配计算得到相似度表示,地磁信息的可信度由地磁匹配计算得到相似度表示,基于可信度的联合定位求得总的位置点相似度:

(13)

式中:WP和WM分别为路径匹配和地磁匹配求得可信度所占的权重,是通过实验训练得到的经验值。将路径点相似度与地磁相似度加权求和,根据计算结果找出与基准库中相似度最高的点,即为最终位置估计点。

当在定位区域内存在如WIFI等其他确定性信息时,可将这些信息融合到可信度计算中,增加定位的稳定性和提高定位的精度。在线定位算法流程图如图4所示。

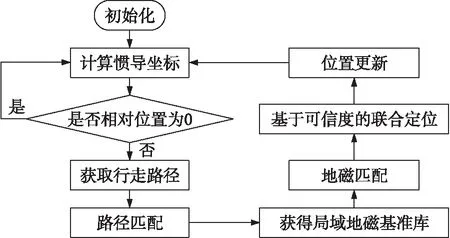
图4 在线定位算法流程图

2 实验设计与结果分析

通过前期的理论研究,项目组设计出一套以Android手机为终端的室内定位系统。系统采用云计算平台作为数据存储和计算平台,具备离线惯导地磁信息采集和在线定位功能。为验证本文提出算法的效果,项目组把基于GINPC算法的室内定位系统在真实的学生公寓中进行了实验测试。

2.1 实验环境设置

实验选择在人口密集的学生公寓中进行,整个学生公寓分为A,B,C三栋,三栋分别通过走廊进行连接,实验选取一层楼作为实验环境,每层有54间房子。实验共采集11个轨迹段,每个轨迹段约15 m,生成惯导地磁基准库,并在实验区域随机行走,记录室内定位的整个过程,其中实验应用系统和实验场景图如图5所示。

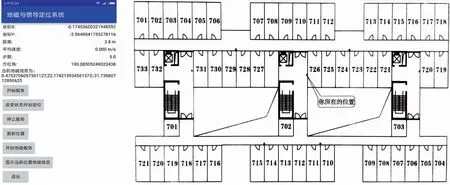
图5 实验应用系统和实验场景平面图

2.2 地磁与惯导联合定位实验

在实验区域对11个轨迹段进行分段采集地磁、惯导坐标和方位角等信息,建立惯导地磁基准库。在Android手机中打开采集软件,输入初始坐标,匀速行走,到达分段末时停止,完成一段路径信息的采集。利用此方法进行其他路径段信息的采集,完成惯导地磁基准库的数据构建。

在线阶段打开Android手机定位软件,输入初始位置点,在采集区域随意走动,利用本文提出的GINPC联合定位算法进行定位,并实时记录每次定位结果,以便接下来进行对比分析。

2.3 定位结果分析与对比

2.3.1 步长估计有效性检测

为了验证行人步长估计模型的有效性,通过模型的训练获得训练参数,对步长模型进行实验验证,每次行走20步,以不同的路径进行10组实验,如图6所示,纵坐标为每组实验实际行走的平均步长和通过步长模型预测得出的步长,横坐标为测试实验数据组数。

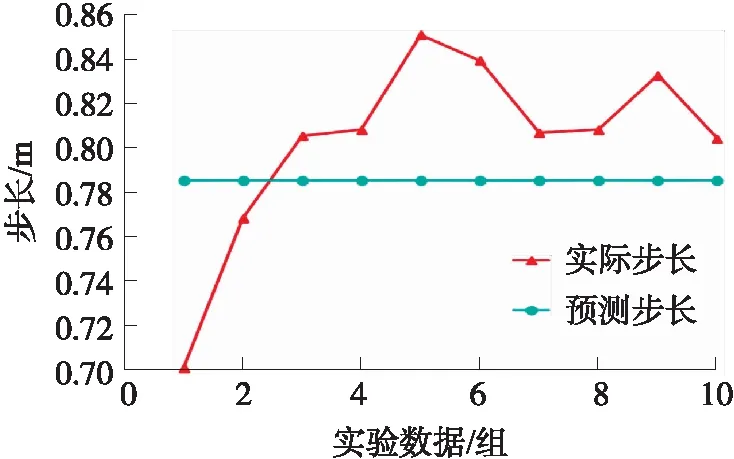
图6 步长估计实验结果图

根据上述实验结果,可以对步长实验结果做一个统计。由表2可知,在不同参数下,60%的步长估计误差在0.02 m左右,80%的步长估计误差在0.05 m以内,步长估计的平均误差为0.04 m。可以看出,步长估计模型精度较高,满足惯导信息的有效性要求。

表2 步长估计实验结果

2.3.2 惯导地磁基准库有效性检测

标准地磁基准库通过对区域进行网格划分来测量构建,需要进行费时费力的网格划分,但具有较为准确的优势。本文提出的惯导地磁基准库是基于路径段的惯导测量来构建,只需要路径段测量即可完成。如图7所示,对学生公寓进行地磁基准库构建时,惯导地磁基准库与标准地磁基准库所获得的地磁信息大致相同。

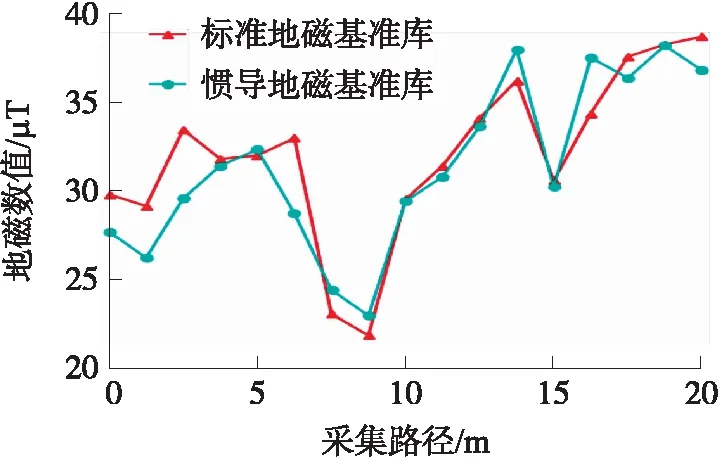
图7 相同路径地磁信息对比

利用以上两种方法获得离线基准库后,在在线阶段使用传统定位方法进行定位实验,来比较定位精度。如图8所示,使用标准地磁基准库和惯导地磁基准库的平均定位误差分别为2.3 m和2.1 m。惯导地磁基准库在保证快速获取地磁基准库的基础上也保证了地磁信息的有效性。

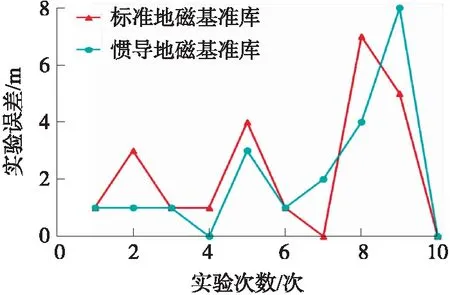
图8 定位实验误差

2.3.3 GINPC定位算法实验与对比分析

在以上所选实验环境内进行实验,比较本文方法、传统地磁定位和惯导辅助地磁定位[3]的定位性能。如图9所示,选取实验定位测试中的一段测试路径进行比较,红色三角形为真实行走路径,青色圆形为惯导辅助地磁获得路径,蓝色菱形为GINPC定位获得路径,从图中可以看出,GINPC定位算法获得路径更加接近真实路径。

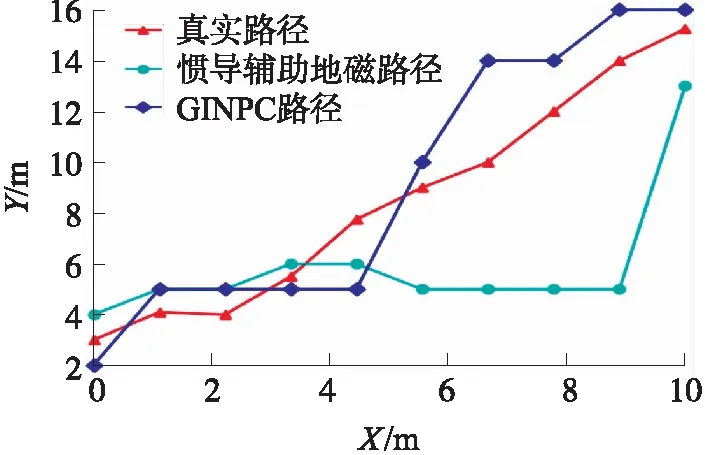
图9 不同定位方法路径对比图

如图10所示,三种定位方法都能保证较好的定位精度,但是传统地磁定位和惯导辅助地磁定位由于确定性信息比较单一,存在较大的偶然误差,而GINPC定位算法具有较好的定位稳定性。

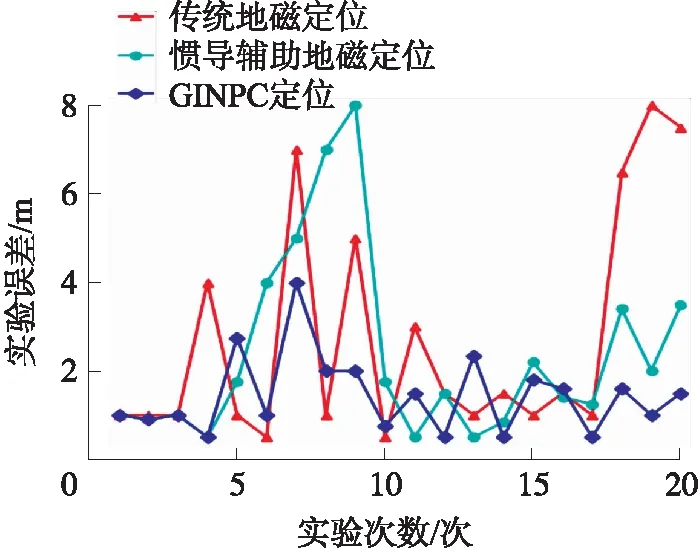
图10 定位结果对比图

如图11所示,GINPC定位算法达到了85%情况下定位误差在2 m以内,而其他两种方法的2 m内的误差百分比分别为65%和60%。由表4可以得知GINPC定位算法对比传统地磁定位和惯导辅助地磁定位的平均误差分别减少了46.7%和40%。惯导辅助地磁定位缩短了87%的定位时间,GINPC定位算法在增加了确定性信息的比较计算同时,缩短了59%的定位时间,保证了定位时间不过长。实验结果表明通过将地磁与惯导的确定性信息进行融合,可以有效的提高室内定位精度。

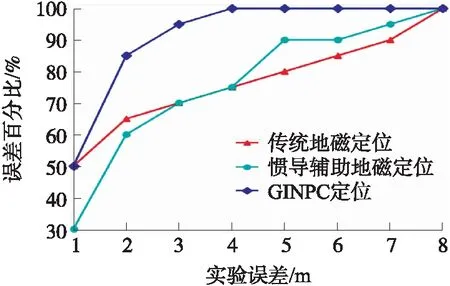
图11 定位误差百分比图

表4 定位结果

3 结论

本文提出了一种快速构建惯导地磁基准库的方法,并提出了基于可信度的联合定位算法。该算法离线阶段无需划分网格,直接采集数据构建基准库,在线阶段融合惯导和地磁确定性信息,通过可信度计算位置估计点。实验结果表明,本文算法有效缩短了离线阶段基准库的构建时间并提高了室内定位的精度,具有较好的稳定性和普适性。同时,在商场、医院等场合内,如果有其他已存在的确定性信息时,可以通过对可信度算法扩展的方式融合更多的确定性信息,提高定位系统的定位精度和稳定性。