基于多电容传感法的多电极阵列微流控芯片内高浓度粒子迁移检测*

范大勇,姚佳烽

(1.东南大学建筑设计研究院有限公司,南京 210096;2.南京航空航天大学机电学院,南京 210016;3.马鞍山南马智能制造研究所有限公司,安徽 马鞍山 243000)

在生物医学微流控领域,研究微尺度粒子如血细胞、细菌、微量DNA在浓度密集时的运动是分析粒子从而获得高控制精度的关键[1-5]。例如,在浓度密集粒子下对血细胞进行处理可以形成具有特异性的靶向血细胞,这对生物和医疗系统的发展具有重要意义。在血细胞分离方面,细胞粒子迁移的研究可以应用于造血干细胞及各种血细胞(白细胞、红细胞、血小板)的采集,并进行血浆置换治疗各种血液系统、免疫系统疾病、代谢系统疾病、急性中毒、肝病、神经系统等疾病,并推动干细胞基础与临床研究。

通常,微通道宽度与粒径的比值相对较小并且雷诺数相对较低。在这种流动条件下,颗粒不会沿着流场线流动而是移动到颗粒迁移的平衡位置。Segre和Silberberg通过实验观察到,在浓度ξ=0.5 vol%的情况下,颗粒在壁上0.6D处积聚,所以之前的许多研究都集中在从理论或模拟的角度来分析低浓度粒子下的粒子迁移[6-7]。Saffman提出了关于粒子迁移的第一个理论解释,他的分析表明,相对于通过粒子中心的流线,在线性剪切流中,施加在粒子上的力与粒子的滑动速度成比例,这个力被称为剪切梯度引起的升力。它导致粒子从中心区域迁移出去,直到碰到壁面反弹,最终沿粒子方向位于壁面前。当颗粒移动到壁区域时,壁效应引起的升力将粒子推离壁区域,最终,粒子的方向位于中心前方。剪切梯度引起的升力和壁面效应引起的升力稳定地对颗粒产生双向作用,可以得到颗粒迁移的平衡位置[8-10]。另一方面,有关人员也展开了基于实验条件下的颗粒迁移的研究,例如Liang等人得出了dp=5 vol%、10 vol%的粒子在ξ=0.5 vol%的低浓度下的迁移特性[11]。他们的研究表明,当施加壁效应力时,粒子远离壁区域,导致颗粒沿中心流线聚集。在不同dp、D、Re和ξ条件下,微通道中的粒子迁移研究的总结如表1所示。在不同ξ条件下,粒子周围的局部流动是不同的,因此对粒子迁移的影响也是不同的。结果表明粒子迁移受ξ影响很大,并且取决于颗粒之间相互作用的程度。

然而,对于基于实验条件下的剪切流引起的粒子迁移的详细研究仍显不足,并且没有给出在高浓度ξ状态下的实验特性。由于光线在高密度流中的不可传输性,所以使用传统方法检测高密度流ξ中的粒子迁移存在一定困难。目前,研究高密度流ξ下剪切力引起的粒子迁移特性,对血液或人类细胞方面的研究也有着重要意义。因此,为了得出并讨论高密度流浓度ξ对粒子迁移的影响,有必要对高密度流ξ剪切力引起的粒子在微通道中的迁移特性进行研究。

为了克服传统方法在检测高密度流ξ中的粒子迁移方面的困难,在之前的研究中,已开发出了多电极阵列的微流控芯片[18-19],采用了能够实现传感电极高速转换的多电容传感法[20]。多电容传感法通过测量电极对之间的电容来评估粒子分布的介电常数。首先在微流控芯片中使用多电容传感法研究密度ξ对粒子迁移特性的影响。分别分析dp=1.3 μm,1.5 μm和2.1 μm的粒子在中密度ξ=3.0 vol%和高密度ξ=10.0 vol%下的不同迁移特性。然而,对在低密度ξ=0.3 vol%到较高密度ξ=4.0 vol%范围内粒子迁移特性的研究还没有展开。

作为实现宽ξ范围内粒子迁移特性研究的第一步,在密度ξ=0.3 vol%～4.0 vol%范围内,通过壁和中心区域的电极对使用多电容传感法来测量电容参数。根据测得的电容,通过改进的麦克斯韦尔模型计算出壁和中心附近区域处标准颗粒的浓度(1-φ)。根据计算出的(1-φ),壁附近区域的的流向迁移率Ψwall和中心附近区域的流向迁移率Ψcenter,以及上游截面zUS和下游zDS处的流向迁移率也可以分别确定,根据流向迁移率就可以讨论密度ξ对粒子迁移的影响。

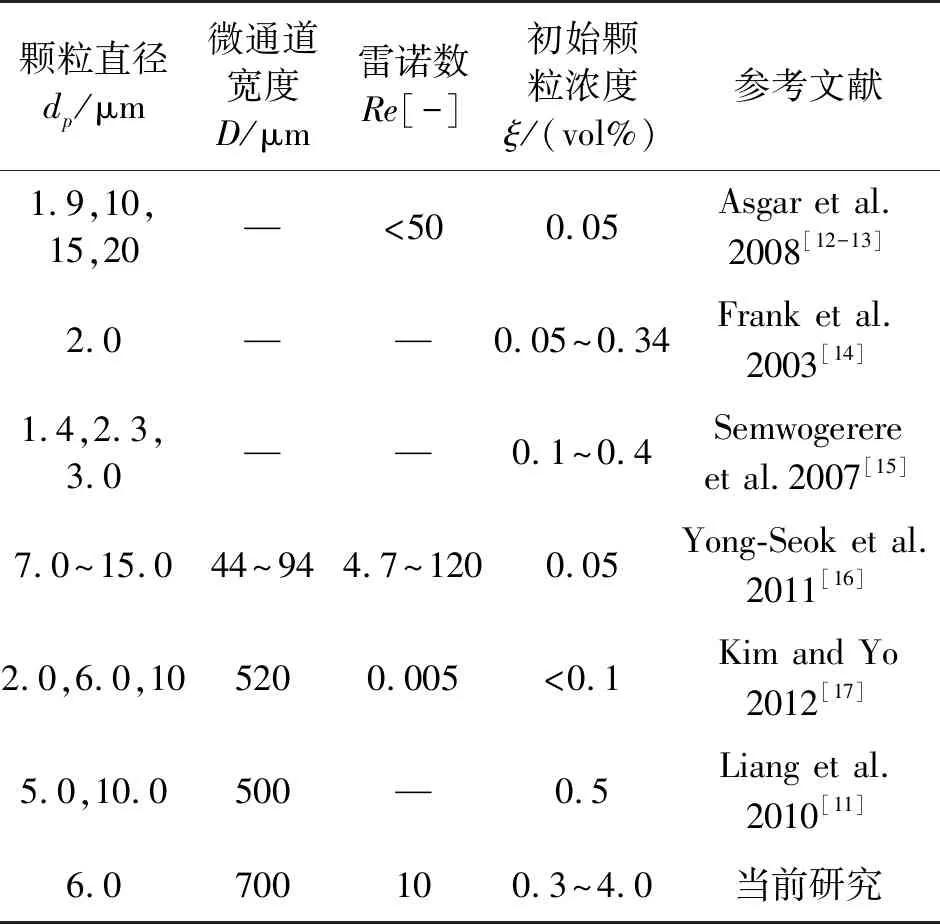
表1 微通道中颗粒迁移研究汇总

1 实验

1.1 实验设备

如图1所示,实验设备由两个注射泵,一个微流控芯片,一个电容测量系统和一台计算机组成。具有最小步进速率1步进/30 s的注射泵(IC3100,KD Scientific,USA),用来控制进入微流控芯片两个入口的流量在60 mL以内。Y形微流控芯片有两个角度θ=30°的入口,左侧的用于流体注入,微流控芯片截面的直线长度z=20 mm,其中五个横截面嵌入了多电极阵列,芯片有两个角度θ=30°的出口,右侧的用于流量排出。

多电极阵列微流控芯片包含一个连接器,传感电极和电路板。在微流控芯片中构建稳定的连接系统,以避免微通道电极尾部和电容测量系统之间产生不稳定的测量条件,来降低噪声影响。连接系统由弹簧销,顶部和底部电路板,插针连接器和中央板组成。弹簧销将电极尾部和电路板连接起来。顶部和底部电路板是用于从弹簧针脚向针脚连接器发送数据的平面电极连接器。中央板支撑着微通道和电路板。

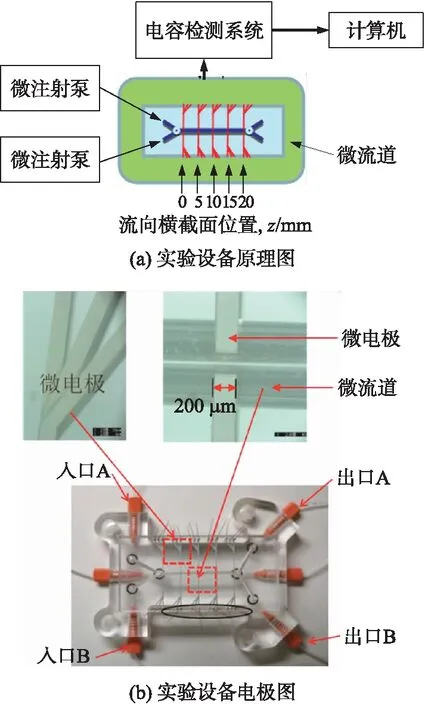
图1 实验设备

图2给出了微通道的详细配置,其中图2(a)是微通道的三维视图,图2(b)是微通道的横截面图。电极材料是铂,基板材料是石英玻璃。坐标系x,y和z的原点位于菱形横截面(x-y平面)的中心点和距离两个入口连接点8 mm处(z方向)。在微通道中有一个径直的菱形截面,其长度z=20 mm。微通道的轴向方向有五个横截面布有电极阵列,每个横截面相距5 mm,其中上游横截面位于z=0 mm处的第一横截面,同时下游横截面位于z=20 mm处的第五横截面。微通道的菱形槽横截面在x和y轴方向上的宽度D=700 μm,表面嵌入了12个菱形截面角θ=45°的多层电极。电极宽度沿着y轴方向且we=75 μm,电极长度沿着x轴方向且le=200 μm。嵌入微通道横截面的传感电极距离基板的长度沿着y轴方向且ls=100 μm。该芯片采用MEMS技术,把电极与石英玻璃逐层叠加进行了加工,详细加工方法可参考相关文献[16,21]。图2(c)给出了横截面底部两对电极加电压时的电场分布仿真分析图,可以发现,电极对产生的电场可以覆盖相应区域,而其他区域几乎不受影响。因此该横截面可以用来实现粒子浓度分布的检测。

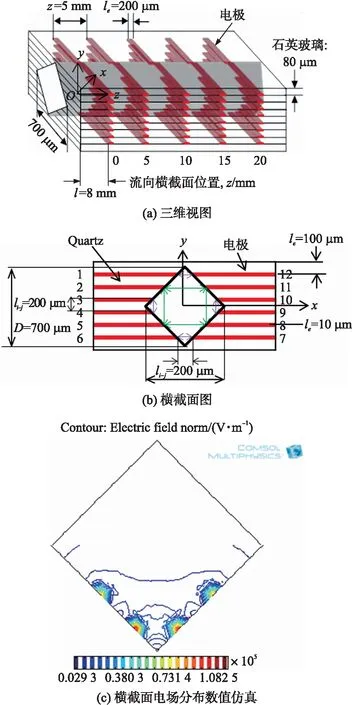
图2 微通道多电极阵列分布图

1.2 实验方法和条件

如图2(b)所示,十二个选定的多电极阵列连接起来,以测量用于分析粒子迁移的电容。根据电场数值仿真计算结果与实验结果(见图2c),发现电极对组合产生的电场在电极对之间较大,其他位置较弱,为了获取更强的检测信号,故采用了电极对1-12,3-4,6-7,9-10及2-11,2-5,5-8和8-11。并且,为了进行分析讨论,在横截面中定义了两个区域,即:墙附近区域(分配有菱形4个顶点处的箭头)和中心附近区域(分配有菱形中部构成正方形的4个箭头)。在微通道横截面中,为了容易理解粒子迁移行为,将壁附近区域和中心附近区域定义为在横截面上的位置。对于每个定义区域,在下游横截面处测量电极对i-j之间的电容Ci-j。通过电极对1-12,3-4,6-7和9-10的测量给出了壁附近区域的信息,而通过电极对2-11,2-5,5-8和8-11的测量给出了中心附近区域的信息。壁附近区域电极对之间的距离li-j=200 μm,而中心附近区域电极对之间的距离li-j=500 μm。

去离子化的粒子悬浮水溶液通过注入泵产生的压差由入口注入,控制流速Q=0.049 m3s-1。由Q和微通道宽度D计算出平均流速u=2.0 ms-1,对应于粒径dp=6.0 μm,雷诺数Re=10和粒子雷诺数Rep=12时的Poiseuille流动区域。去离子水和电介质聚苯乙烯颗粒的相对介电常数分别为εDWr=80.0和εPr=2.5。Ci-j是在不同初始粒子体积浓度ξ=0.3,0.5,1.0,1.5,2.0,2.5,3.0,3.5和4.0 vol%条件下,在下游截面的壁附近区域和中心附近区域测量所得。多电容传感的频率f=12.5 MHz,电压V=4.5 V。此外,在多电容传感中,处于非均匀电场中的去离子化的介电粒子悬浮水溶液会受到介电泳(DEP)力[22-24]。但是,在此次研究中,在E=4.5 V/mm,dp=6.0 μm的情况下产生的DEP力足够小,在10-9N左右,因此忽略检测时候电场造成的DEP力的影响。

1.3 多电容传感法

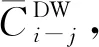
(1)

(2)

(3a)

(3b)

(3c)

式中:li-j是电极对之间的距离,A是电极面积,A=5.0×10-12m2。由于电极属于微米级,只有10 μm厚度,在这种数量级下,电极的倾斜度对电容的影响可以忽略,故采用平行板电容的方式进行计算[19]。利用介电常数,电极之间的标准化粒子浓度(1-φ)i-j可由改进的Maxwell方程计算得到[25]。

(4)

根据方程(4),中心区域和壁附近区域处的标准化粒子平均浓度<(1-φ)>可由四电极对间的平均浓度计算得到

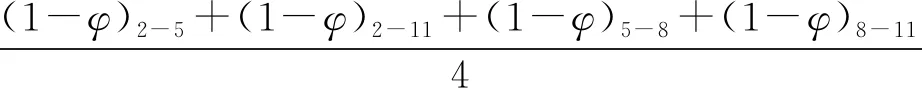
(5a)

(5b)

以上公式中涉及到的参数及其定义见表2。

表2 检测参数及定义汇总

2 实验结果和讨论

2.1 平均电容

图3给出了流动粒子的平均电容,平均电容可通过式(1)得到。在不同初始粒子浓度ξ=0.3 vol%～4.0 vol%条件下,在下游横截面处,表示壁附近区域平均电容,表示中心区域平均电容。在T=100 s测量时间内,10次偏差引起的的不确定度标准误差相当恒定,并且小于7.0%。因此,即使的微分很小,是毫微微法拉阶,也是可接受的。在这项研究中,的结果被分为三个梯度。在低密度ξ=0.3 vol%～1.5 vol%的情况下,当ξ增加时,成比例增加1.30倍。然而,在中密度ξ=1.5 vol%～3.0 vol%的情况下,当ξ增加时,相应地增加1.08倍。同样,在足够稠密的ξ>3.0 vol%情况下,当ξ加时,增加1.07倍。这表明随着ξ增加,在低密度ξ电容也随之增加;然而,在中密度ξ和足够密集的ξ下,无论ξ如何,电容几乎没有增加。这是因为粒子的数量增加,剪切力和粒子之间的相互作用变得更强,这会使粒子在微通道中无法自由移动。

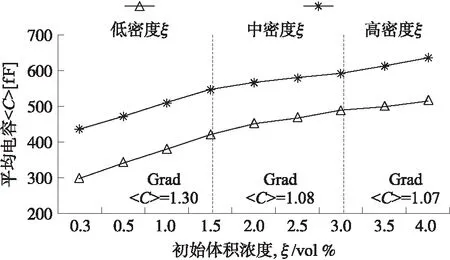
图3 在不同初始粒子浓度下下游横截面处中心和壁附近区域的平均电容

2.2 标准化粒子浓度

图4显示了在不同初始粒子浓度ξ=0.3 vol%～4.0 vol%的情况下,由式(5a)和式(5b)计算的标准化粒子浓度(1-φ),中心附近区域浓度为(1-φ)center和壁附近区域浓度为(1-φ)wall。结果表明(1-φ)的增加与ξ无关。在低密度ξ=0.3 vol%～1.5 vol%的情况下,随着ξ增加,(1-φ)成比例地增加1.40倍。这是因为在低密度ξ状态下,粒子被充分分离以至于粒子之间的相互作用可以忽略。然而,在中密度ξ=1.5 vol%～3.0 vol%的情况下,当ξ增加时,(1-φ)相应地增加1.19倍。在中密度体系下,粒子足够接近,相互之间以流体力学的方式相互作用。同样,在足够密集的ξ>3.0 vol%情况下,随着ξ增加,(1-φ)增加1.05倍。这是因为在足够密集的状态下,粒子间排斥作用强烈产生粒子跟踪,因此粒子之间的相互作用变得更强,使迁移变得困难。

图4 在不同初始颗粒浓度下下游横截面处中心和壁附近区域的标准化颗粒浓度

2.3 流向迁移率

对于标准化粒子浓度(1-φ),使用中心和壁附近两个区域的粒子迁移关系来描述微通道横截面上粒子的迁移特性。引入从上游zUS处到下游zDS处在中心区域的流向迁移率Ψcenter和在壁附近区域的流向迁移率Ψwall,该值可由式(6a)、式(6b)计算得出。

(6a)

(6b)

图5显示了在不同初始粒子浓度ξ条件下,通过式(6a)和式(6b)计算得来的,从上游到下游横截面的中心区域迁移率Ψcenter和壁附近区域迁移率Ψwall。在图中,Ψ=1.0意味着下游到上游之间的(1-φ)是相同的。粒子的数量随着粒子沿着z方向移动而增加,Ψ也随之增加。此外,无论ξ如何变化,Ψwall的流向迁移率都要略高于Ψcenter。这是因为粒子在向下游横截面移动过程中,受到剪切升力作用,粒子从中心区域缓慢地迁移到壁附近区域的某个平衡位置。

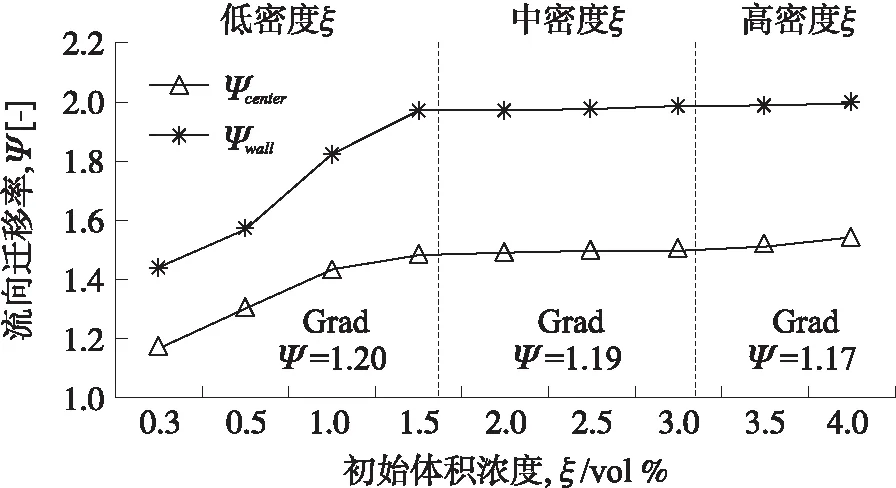
图5 在不同初始颗粒浓度下下游横截面处中心和壁附近区域的流向迁移率

就Ψ和ξ之间的定性关系而言,Ψ随着ξ的增加而增加,而与z无关。在低密度ξ=0.3 vol%～1.5 vol%情况下,当ξ增加时,Ψ增加1.26倍。然而,在中密度ξ=1.5 vol%～3.0 vol%和足够密集ξ>3.0 vol%的情况下,Ψ的方差几乎保持不变且是线性持续的。这是因为在高密度流ξ中,相同体积内的粒子数量相对较多,导致相邻子粒之间距离较近,粒子之间强烈的相互作用造成较少的粒子迁移。

定量考虑,Ψ在低密度ξ=0.3 vol%～1.5 vol%情况下增加了1.20倍,在中密度ξ=1.5 vol%～3.0 vol%的情况下增加了1.19倍,在足够密集的ξ>3.0 vol%情况下增加了1.17倍。这意味着在低密度ξ下,随着颗粒从上游向下游移动,颗粒倾向于主动向壁面附近区域集中,而在高密度ξ下,粒子之间的相互作用变强,相比于低密度ξ而言,粒子迁移不再起主要作用。该现象可以由雷诺数对剪切诱导升力的影响比对壁诱导升力的影响更为显著来解释。也就是说,雷诺数越大,剪切梯度升力越占主导地位,颗粒平衡位置越靠近壁面移动。随着粒子浓度的增加,颗粒被迫保持彼此接近,并且在高浓度的情况下导致颗粒-颗粒相互作用的大幅增加。结果,一部分颗粒被推离平衡位置,使得粒子迁移变得更加困难。

2.4 粒子-粒子相互作用

为了确定粒子在微通道中迁移的平衡点位置,设定相邻颗粒之间的特征长度为L,是在压力驱动下能够在微通道中实现剪切粒子迁移并能够充分流动的估计距离。图6显示了在dp=6 μm,不同粒子浓度ξ=0.5 vol%～5.0 vol%的情况下,相邻颗粒之间的特征长度L与颗粒数量Np的趋势图。

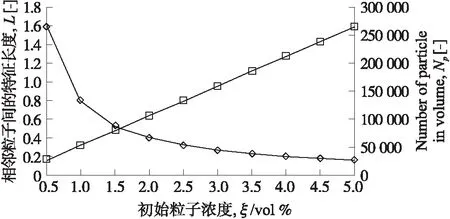
图6 粒径dp=6 μm时不同初始体积浓度下相邻粒子间特征长度与粒子数的趋势图

假定流动粒子是单向流动并且由于剪切扩散而发生迁移,在不同初始粒子浓度ξ=0.5 vol%～5.0 vol%情况下,对于粒径dp=6 μm的粒子,在流向的垂直方向上,粒子的平均位移大致与Butler等[26]给出的充分流动流体的无量纲距离相同,该值可由式(7)计算得出。

(7)

对于流过微通道的迁移粒子,任何单个颗粒都要在微通道宽度D的小范围内移动并迁移,并达到完全流动状态。不同ξ条件下,在粒径dp=6 μm的平衡位置处,微通道一定体积内的粒子迁移数量Np可由Asakura等[27]给出的方程(8)计算得出。

(8)

从图6可以看出,相邻颗粒间相互作用的特征长度在ξ=1.5 vol%时开始快速下降,并继续下降直至ξ=3.0 vol%,其中颗粒间相互作用的特征长度在ξ=5.0 vol%下几乎恒定,截止值为0.25。而颗粒间相互作用的特征长度在值为0.15时截止。另一方面,随着单位体积内颗粒数量的增加,在中密度ξ和足够密集ξ的情况下,微通道横截面单位体积内占据的颗粒量比在低密度ξ下略高。在该图中,L与Np的趋势图显示临界ξ处于ξ=1.5 vol%处。

此外,在不同的ξ状态下,以特定的应力或应变速率测量颗粒之间的表观粘度。结果表明,随着ξ增加,由于最近的相邻粒子之间的相互作用和分离作用,表观粘度也发生变化。在低密度ξ=0.3 vol%～1.5 vol%时,颗粒充分分离以致于相邻颗粒之间的相互作用可忽略不计。在这种状态下,流体在粒子周围流动时需要做额外功,并且颗粒在流体中的旋转,这些都是的表观粘度增大[28]。在中密度ξ=1.5 vol%～3.0 vol%时,颗粒浓度分布均匀。在这种状态下,相邻颗粒之间足够接近,它们以流体动力学的方式相互作用,使得颗粒迁移变得更加困难。在足够密集的ξ>3.0 vol%的情况下,颗粒之间的典型最小分离距离太小,剪切力将流体挤压到颗粒之间的微小间隙中去,导致高应变率下的粘度降低。

3 结论

本文利用多电极阵列微流控芯片的特殊结构,采用多电容传感法,在大量高浓度粒子中测量了标准聚苯乙烯颗粒的迁移规律与浓度。

①随着颗粒向下游横截面移动,粒子浓度ξ增加时,中心附近区域和壁附近区域的标准化颗粒浓度(1-φ)center,(1-φ)wall也随之增加。

②在中密度ξ=1.5 vol%～3.0 vol%和足够密集ξ>3.0 vol%的情况下,随着ξ增加,(1-φ)的百分比增量逐渐减小。这是因为颗粒间相互排斥并导致了颗粒跟踪,因此颗粒之间的相互作用变强并使得迁移变得困难。

③中心附近区域和壁附近区域处的流向迁移率Ψcenter,Ψwall随着ξ增加而增加,然而在高密度ξ=1.5 vol%～4.0 vol%的情况下,Ψ的方差几乎线性恒定。这是因为在高密度流ξ中,相同体积内的粒子数量相对较多,导致相邻子粒之间距离较近,粒子之间强烈的相互作用造成较少的粒子迁移。

本文提出的多电容传感法可以有效测量高浓度粒子中目标颗粒在流体中的迁移规律与浓度,对研究生物医学中特异性的靶向血细胞具有重要的指导意义。