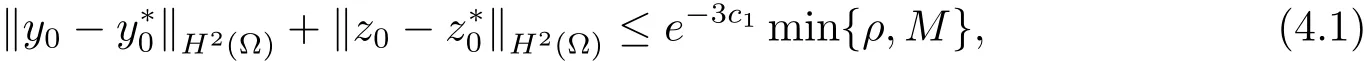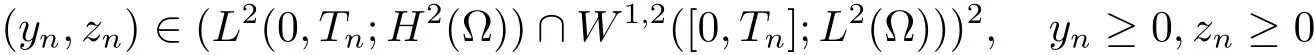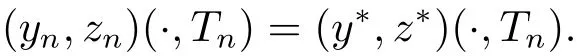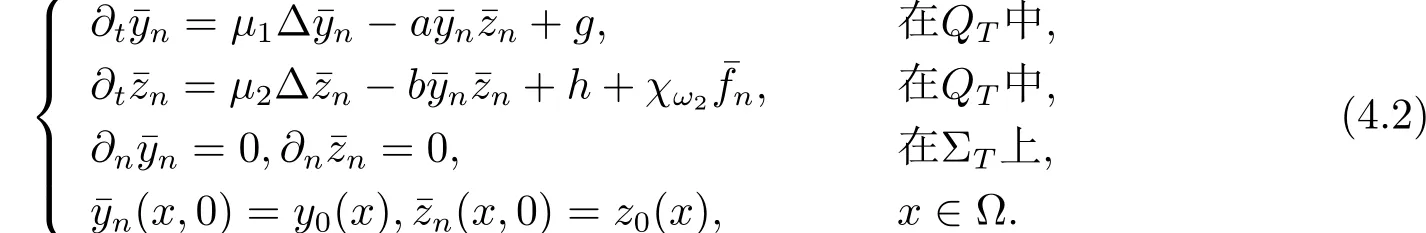竞争型反应扩散方程的正解与时间最优控制
刘远凯,张 亮
(武汉理工大学数学系,湖北武汉 430070)
1 引言
设Ω⊂Rd(d≥1)为带光滑边界∂Ω的有界区域,ω为Ω的非空开子集.记QT=Ω×(0,T),ΣT= ∂Ω×(0,T);并以|·|p和k·kp分别记函数空间Lp(Ω)和Lp(QT)(1≤ p≤ ∞)的范数.对于任意的Banach空间X,用X2表示笛卡尔积X×X.设
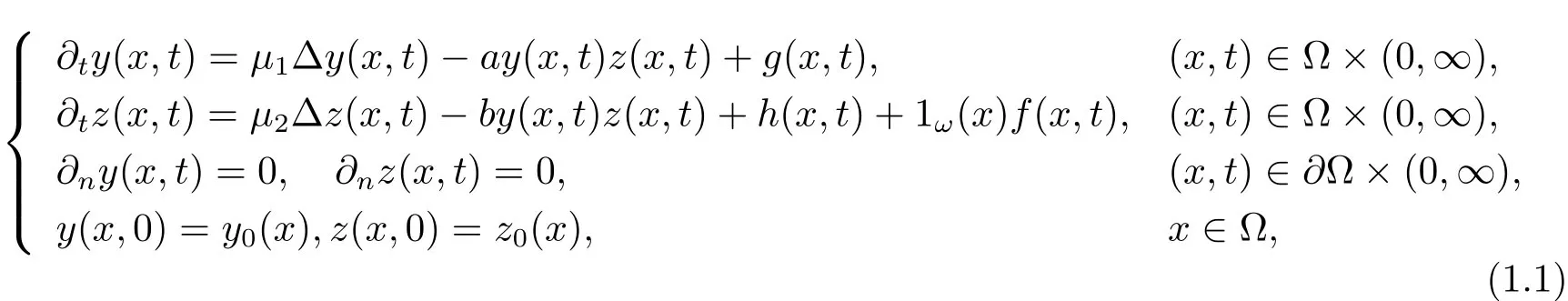
其中y=y(x,t)和z=z(x,t)分别表示两种物质的密度;∂ny=∂y/∂n,∂nz=∂z/∂n,n表示边界∂Ω的外法单位向量;给定的函数g=g(x,t)和h=h(x,t)表示物质的输入;µ1和µ2是正常数,表示扩散系数;a和b为非负常数,表示反应常数;y0=y0(x)和z0=z0(x)表示初始值;f=f(x,t)为控制函数,1ω为集合ω上的特征函数,1ωf表示控制函数经子集合ω作用于系统.为了简化符号,在不发生混淆的情况下,我们省略函数表达式中的x和t.
给定时刻T,考虑如下形式的反应扩散系统:
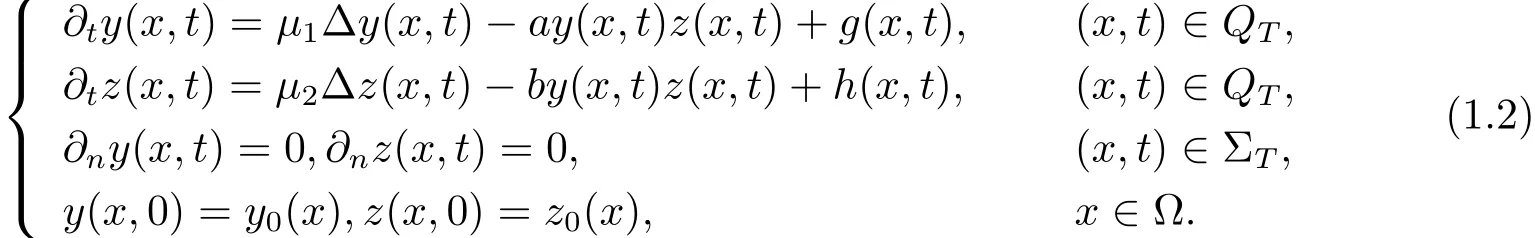
系统(1.2)在生物和化学方面均为非常重要的模型,相关的工作非常丰富.因为物质的密度为正值,所以仅考虑系统(1.1)和(1.2)的正解.为此,给出如下的假设
(H1)g,h∈L∞(0,∞,L∞(Ω)),g(x,t)≥M0,h(x,t)≥ M0a.e.(x,t)∈Ω×(0,∞);
(H2)y0,z0∈ L∞(Ω)∩H2(Ω),y0(x)≥ m0,z0(x)≥ m0a.e.x∈ Ω,其中M0,m0均为正常数.
本文将证明,在假设(H1)和(H2)的条件下,存在正常数M∗,使得系统(1.2)的解(y∗,z∗) 满足
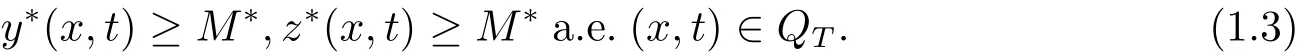
这样的解称之为系统(1.2)的正轨迹.以此正轨迹为目标函数,考虑系统(1.1)关于正轨迹(y∗,z∗)的能控性问题和时间最优控制的存在性问题.具体地,设ρ>0,记
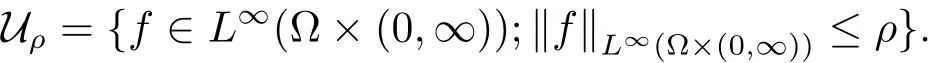
称系统(1.1)对于正轨迹(y∗,z∗)在时刻T是局部精确能控的,如果对于一定范围内的初值(y0,z0),都存在控制f∈Uρ使得系统(1.1)相应的解满足
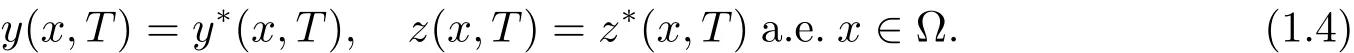
此外,希望系统(1.1)的解保持非负,即y和z满足y(x,t)≥0,z(x,t)≥0 a.e.(x,t)∈QT.设
=={T>0;存在控制f∈Uρ使得系统(1.1)在时刻T处精确能控到目标(y∗,z∗)(·,T)},并考虑如下的时间最优控制的存在性问题

亦即系统(1.1)精准达到目标(y∗,z∗)的最短时间是否存在的问题.该问题可以解释为系统在控制的作用下在最短的时间内与给定的轨迹同步.
关于非线性抛物型方程解的存在性问题,相关的研究工作比较深入,利用多种方法和技巧可以研究解的存在性、唯一性等性质[1−2].由抛物型偏微分方程或方程组刻画的分布参数系统的控制问题,尤其是能控性问题和时间最优控制问题,近二十年以来一直受到持续关注,目前已经有一些经典的结果,比如文献[3–6].关于抛物型方程组的能控性和时间最优控制问题,因其特有的数学结构以及广泛的实际应用背景,近年来愈发引起关注.在文献[7]中,作者首次研究了一类反应扩散方程的局部能控性问题,但是由于在同一内部区域对每个物质施加控制,因此该问题可以转化为单一的抛物型方程的能控性问题.在文献[8–10]中,作者考虑了抛物型方程组在一个控制下的能控性问题或时间最优控制问题.目前,关于抛物型方程组在一个控制的能控性问题仍然有一些公开的难题没有解决.关于抛物型方程的时间最优控制问题,最近在文献[11–15]中出现了一些最新的进展.本文所研究的内容是对文献[7]和[9]的结果的改进.首先,本文所研究的模型与文献[7]和[9]不同,非齐次项g与时间变量有关,且控制施加在一个方程之上,因此,本文的结果是文献[7]和[9]的推广.其次,本文利用上下解方法得到系统(1.1)的严格正解,这是本文的主要结果之一.最后,本文探讨了系统(1.1)关于正轨迹(y∗(x,t),z∗(x,t))的时间最优控制的存在性问题,该问题可以解释为系统在控制的作用下和预定的轨迹能否在最短的时间内同步,这是与文献[7]和[9]的不同之处.
2 正解的存在性
本节给出了系统(1.2)存在唯一正解的证明,得到如下结果.
定理2.1假设(H1)和(H2)成立,则系统(1.1)存在唯一正解
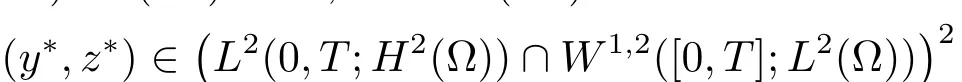
并且存在常数C,M∗>0,使得解满足(1.3)式和不等式
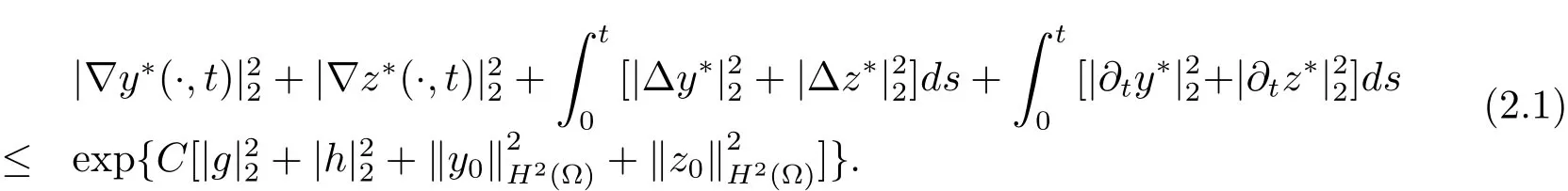
为了证明这个结论,给出如下引理.
引理 2.1令 0< α <1.设g,h满足g,h≥ M0,y0,z0∈Cα(Ω)满足其满足 y(x,t)≥ M∗,z(x,t)≥ M∗,(x,t)∈QT.且存在一个足够小的常数M∗满足0<2M∗≤m0,则系统(1.2)存在唯一解
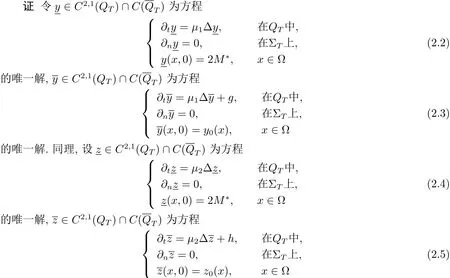
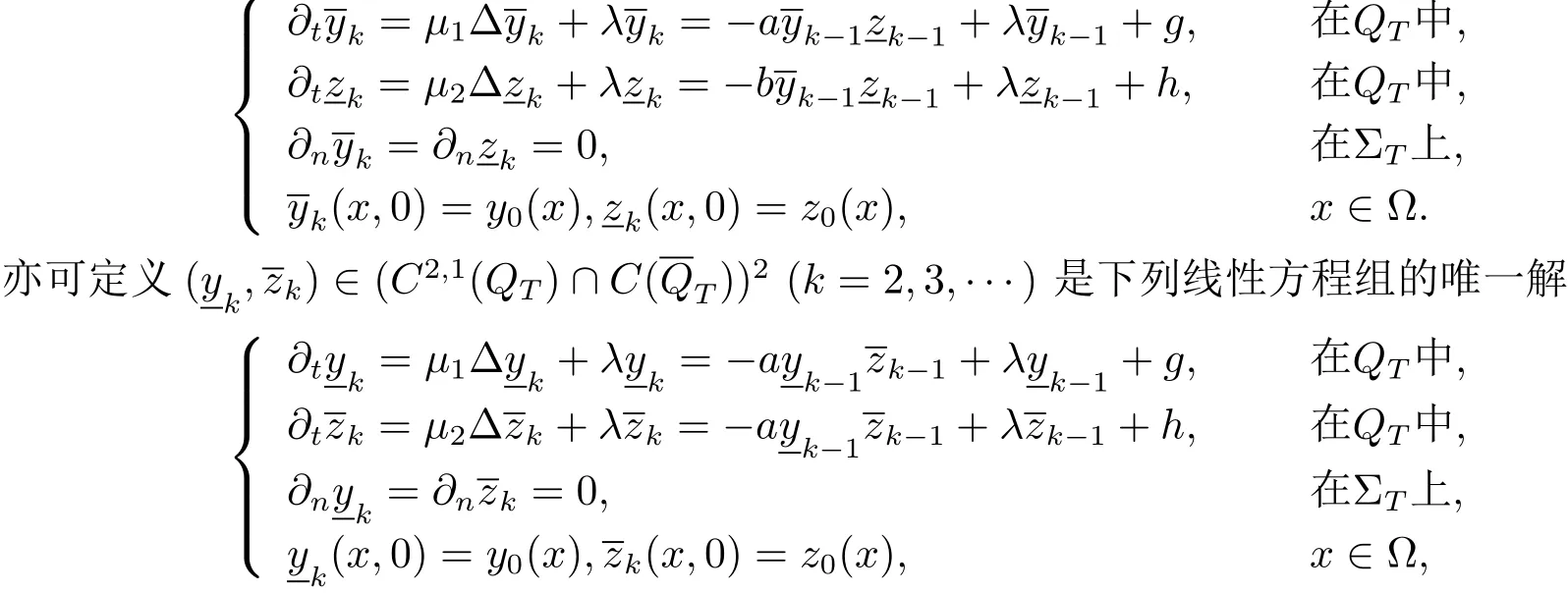
这里λ为一足够大的常数.根据比较定理,得递推关系

引理 2.2设
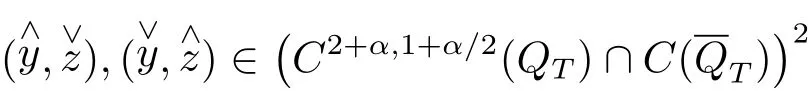
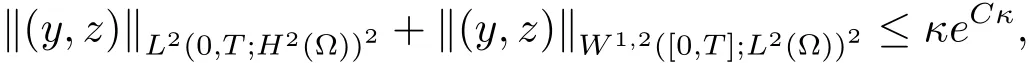
定理 2.1的证明构造光滑函数序列使gn,hn在L
2(QT)中强收敛于g,h,y0n,z0n在H2(Ω)中强收敛于y0,z0,并且m0.利用引理2.1可以得出,对于任意的n,系统(1.2)都至少存在一个解
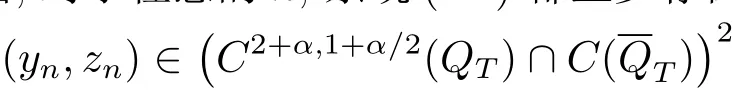
3 能控性
3.1 在一个控制下线性系统的零能控性
这一节研究具有一个控制的线性系统的零能控性:
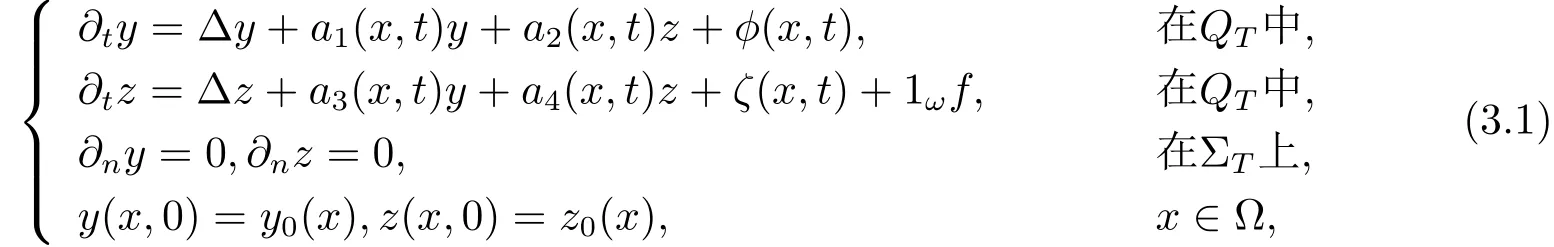
(H3)在ω中存在一个非空子集ω0⊆ω和正常数σ,使a2(x,t)≥σ或a2(x,t)≤−σ a.e.(x,t)∈ ω0×(0,T).
考虑线性系统(3.1)的伴随系统
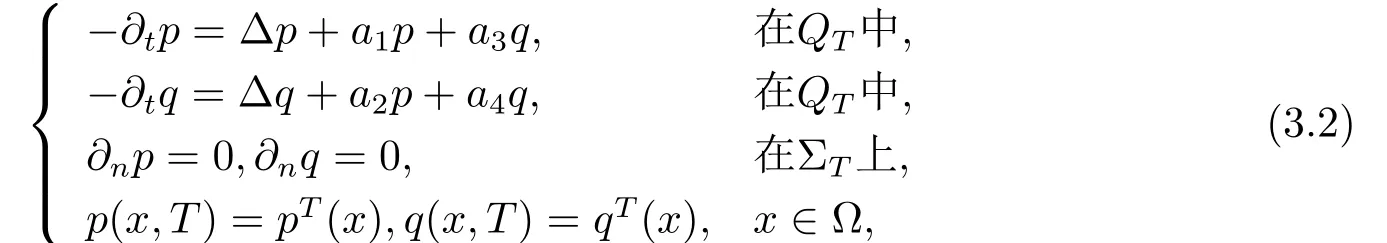
其中pT,qT∈L2(Ω).为了得到系统(3.1)的零能控性,我们需要一个全局的Carleman不等式和伴随系统(3.2)的能观性估计.令ω0⊂⊂ω0是Ω中的非空子集,且有函数

有如下适合于线性方程组的Carlman不等式.
引理3.1[9]设条件(H3)成立.存在仅依赖于Ω,ω0,ω0,kaik∞的常数λ1>1,使得对任意的λ>λ1,s>γ(λ)(T+T2),系统(3.2)的解(p,q)都满足
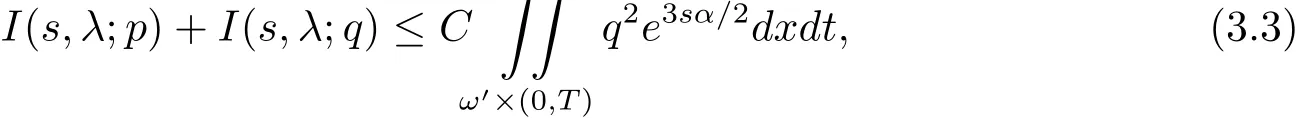
根据引理3.1,有如下能观性估计.
引理3.2[9]设条件(H3)成立,T>0.存在常数λ>1且γ(λ)>4,s>0,系统(3.2)的解(p,q)都满足
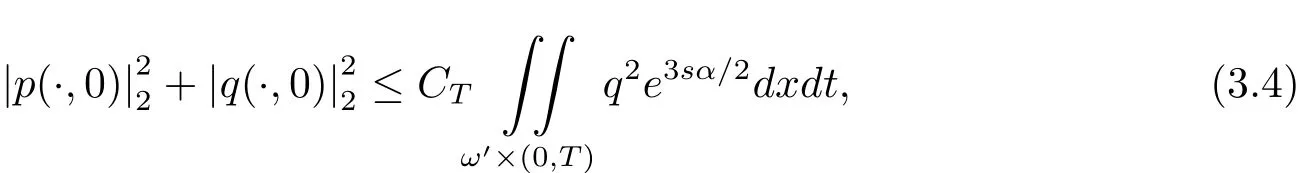
其中常数CT形如
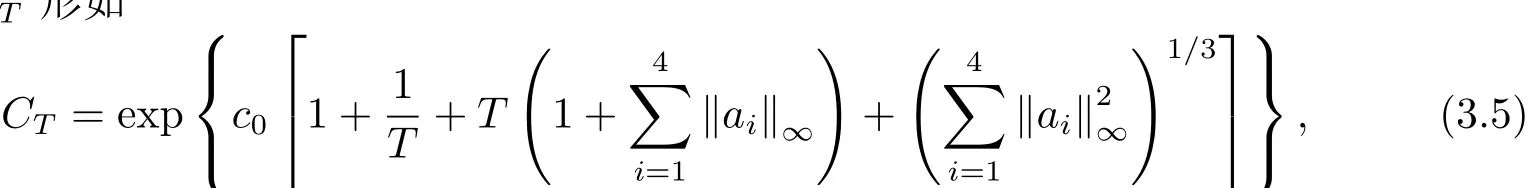
这里c0是依赖于Ω,ω0,ω0的正常数.
此外,需要另一种能观性估计,根据引理3.1和3.2,利用文献[15]中的方法可以得出
引理3.3设条件(H3)成立,存在正常数K 和s,使系统(3.2)的任意解(p,q)都满足
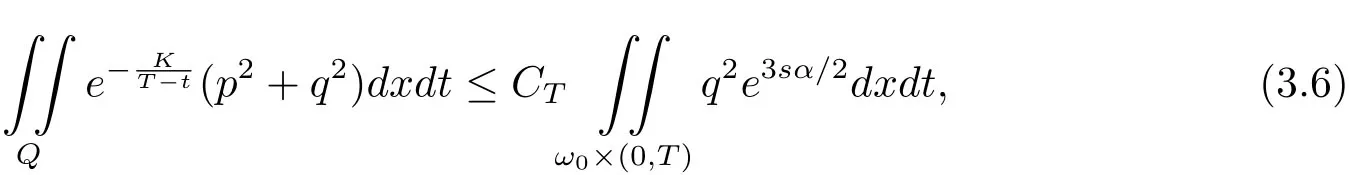
其中CT是由(3.5)式给定,K=8γ2(λ1)(1+T),λ1和γ(λ1)由引理3.1给出.
定理3.1设条件(H3)成立,如果存在正常数K,使得非齐次项φ,ζ满足
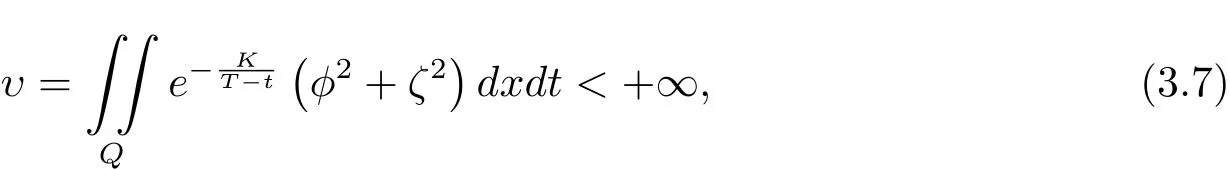
则称系统(3.1)是零能控的,即存在控制f∈L∞(QT)使得对于任意的(y0,z0)∈L2(Ω)2,系统(3.1)的解(y,z)∈(L2(0,T;H1(Ω))∩C([0,T];L2(Ω)))2都满足y(x,T)=z(x,T)=0 a.e.x∈Ω.此外,控制函数满足如下估计
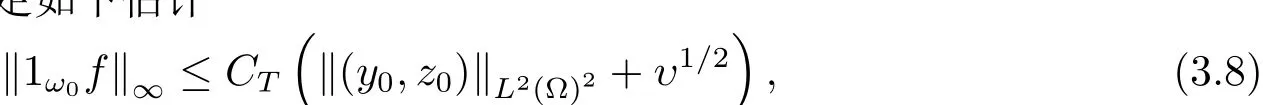
其中CT是由(3.5)式给定.
证设s和λ使不等式(3.4)和(3.6)中成立.对任意的ε>0,考虑如下最优控制问题:
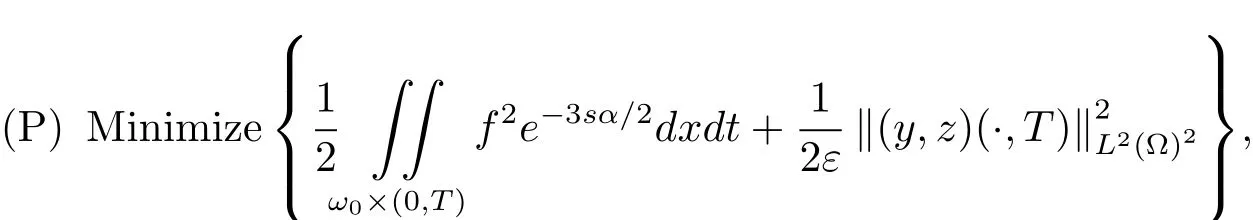
其中f∈L2(QT),(y,z)是系统(3.1)的解.可以验证问题(P)的最优解(fε,(yε,zε))的存在性,利用 Pontryagin 极大值原理[3],fε=qεe3sα/21ω0,其中 (pε,qε)是伴随系统 (3.2)的解,
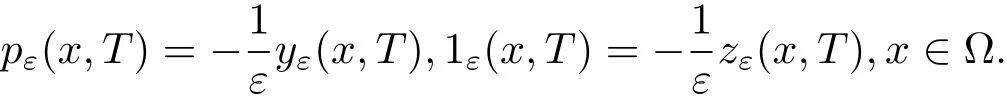
(yε,zε)是系统(3.1)相应于f=fε的解.根据线性系统(3.1),伴随系统(3.2),引理3.2和3.3,可以得出
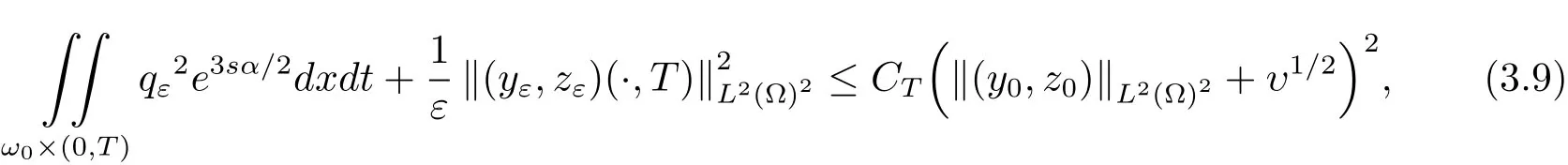
其中CT和υ由(3.5)和(3.7)式给出.利用(3.9)式和引理3.3,可知控制fε满足(3.8)式.由此,存在子列fεk,使得fεk在L∞(QT)中弱∗收敛于f,根据线性抛物型方程的线性性,可以验证系统(3.1)的解(yεk,zεk)对应于fεk收敛到系统(3.1)的解(y,z).最后,利用(3.9)式,可得在Ω中几乎处处都有y(x,T)=0,z(x,T)=0.
注3.1定理3.1的结论应用到两个特殊情形:(i)φ=0,ζ=0;(ii)对某些ε>0,在(x,t)∈ Ω×(0,T −ε)中,φ,ζ满足 φ(x,t)=0,ζ(x,t)=0.
3.2 反应扩散系统的局部精确能控性
本节运用Kakutani不动点定理[3]证明非线性系统(1.1)的局部精确能控性.
定理3.2设(y∗,z∗)为系统(1.2)对应于的一个正解,且满足(1.3)式.令M 就有控制f∈Uρ使得系统(3.11)有唯一正解 满足于(1.4)式. 证设Y=y−y∗,Z=z−z∗,Y0=y0−y∗0,Z0=z0−z∗0,则(Y,Z)满足如下方程组 只须证明系统(3.11)的局部零能控即可.为此,将该方程组线性化,即得 其中 (ξ,η)∈ K. 这里 K={(ξ,η);kξk∞≤ M,kηk∞≤ M} ⊂ L2(QT)2,M 根据(3.13)式和线性抛物型方程的能量估计,有 注3.2定理3.2表明系统(1.1)可以在带有约束条件的控制作用下的局部精确能控.事实上,当控制没有约束时,局部精确能控性对正轨道(y∗,z∗)也是有效的.亦即,对任意满足 的(y0,z0)∈H2(Ω)2都存在控制f∈L∞(QT)使得在T时刻,系统(1.1)的轨迹(y,z)在T时刻能达到目标轨迹 (y∗,z∗)(·,T). 设ω1和ω2为Ω中的开集,至少有一个非空.考虑如下控制系统 推论 3.1设(y∗,z∗)和常数c1由定理3.2给出,如果 (y0,z0)∈ H2(Ω)2满足(3.10)式,则存在控制f1,f2∈Uρ使得系统(3.15)有唯一正解(y,z)并满足y(x,T)=y∗(x,T),z(x,T)=z∗(x,T)a.e.(x,t)∈ QT. 证 不妨设ω2非空.取f1=0,则只需根据定理3.2和引理2.2即可证明. 定理4.1设(y∗,z∗)和常数c1由定理3.2给出,对于任意的(y0,z0)∈H2(Ω)2,若其满足 则时间最优控制问题(TP)至少存在一个时间最优控制. 和 取T≥T1,作辅助函数¯yn如下:¯yn=yn,当(x,t)∈Ω×(0,Tn]时;¯yn=y∗,当(x,t)∈Ω×(Tn,T)时.类似定义¯zn.再做辅助函数¯fn如下:¯fn=fn,当(x,t)∈Ω×(0,Tn]时;¯fn=0,当(x,t)∈Ω×(Tn,T)时.于是(¯yn,¯zn)∈(L2(0,T;H2(Ω))∩W1,2([0,T];L2(Ω)))2为下列方程组的解 其中κ为与时间T无关的常数.根据定理2.1中的不等式,可以得到如下估计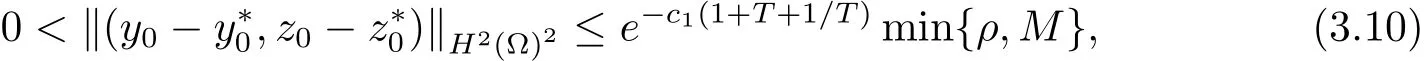
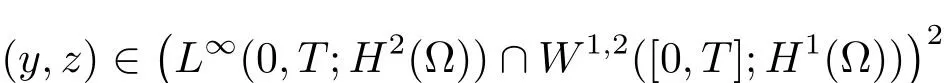
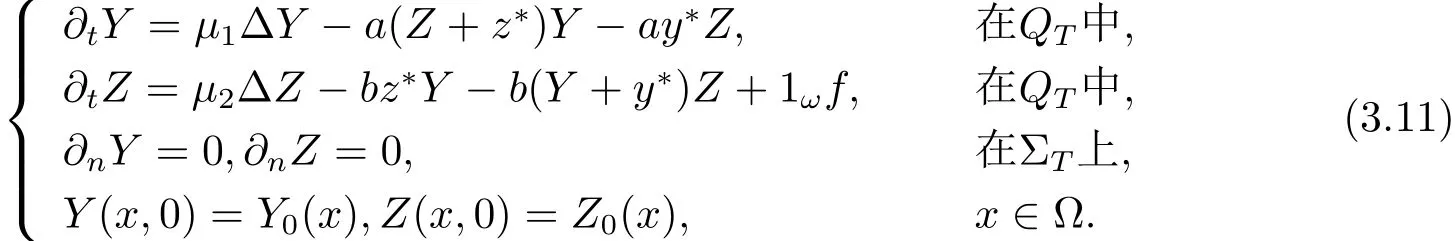
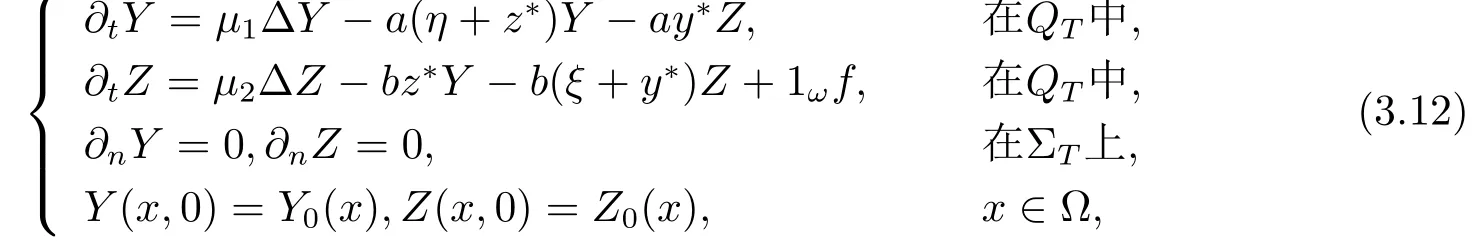
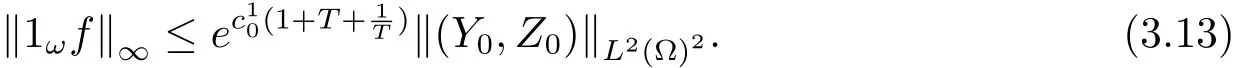
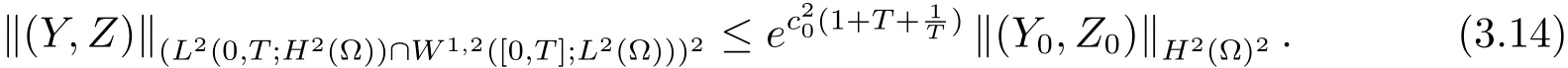
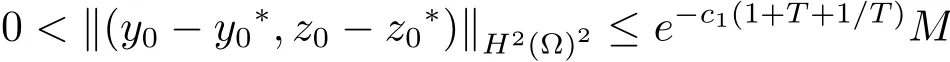
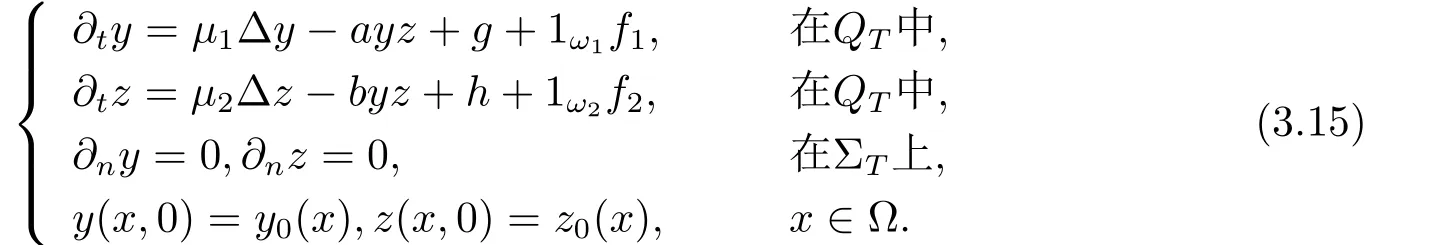
4 时间最优控制的存在性