逆散射问题求解的正则化GAUSS-NEWTON法

闵 涛,仝云莉

(西安理工大学理学院应用数学系,陕西西安 710054)

1 引言

逆散射问题在遥感、无损探测、地球物理、医用成像和雷达目标识别等方面[1−4]有着广泛的应用.但由于此类问题具有非线性、不适定的特点,给数值求解带来了很大困难.20世纪60年代,前苏联数学家吉洪诺夫、伊万诺夫和拉弗伦捷耶夫等提出了不适定问题正则化方法,随后,很多学者对逆散射问题进行了卓有成效的研究.Jost等人[5]提出了逆散射微扰论,Moses[6]和Prosser[7−10]等人对此作了进一步的研究,研究了一维和三维逆散射问题,对解误差进行了分析和估计,随后Newton等人[7−8,11−14]对一维和三维逆散射问题进行了进一步的研究,并对解的唯一性进行了讨论.Colton等人[15−18]利用积分方程方法对声波和电磁波逆问题作了深入研究.其中,对逆散射理论发展贡献最大的是Bleistein[19−26]和Cohen等人[27−29],他们以小扰动理论和Born近似为理论基础,建立了利用Fourier变换等方法进行反演的理论,最终形成了逆散射反演方法.本文在对障碍物的边界进行参数化处理的基础上,将逆散射问题转化为一非线性积分方程,通过数值积分离散,提出利用迭代正则化高斯-牛顿法来求解,并进行了数值模拟.

2 逆散射模型的建立

散射是指由光波、音波、电磁波或粒子在通过均匀介质时,遇到区域大小为Ω、边界为Γ的障碍物而改变其直线运动轨迹的物理现象.为了计算方便,我们主要考虑二维区域并假定散射区域Ω是呈星形的,即在散射区域Ω中,存在连续的正函数R(θ)(0≤θ<2π),使得边界Γ上的点用极坐标表示为(R(θ),θ).假定入射波为波矢为k0的简谐波,即ψin(r)=exp(ik0·r),障碍物中的波数k1是一个常量.令ψsc(r)表示散射区域,总区域满足微分方程

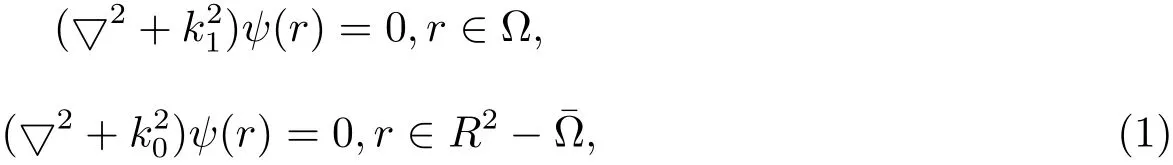
如果平面波正常照射介质柱的轴线,并且电场E的两极沿轴线分布在两端,该散射问题转化为求解方程 (1),其中 ψ =E,波数是真空中的介电常数和磁导率,εr,σ是障碍物的相对介电常数和电导率.

从入射角ϕ处的远场散射数据,得到散射振幅为

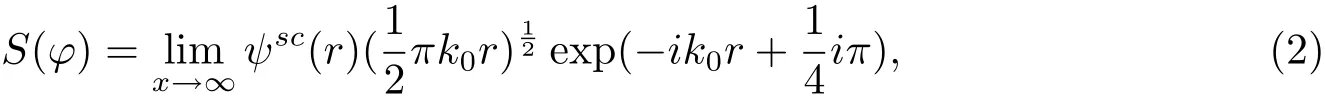
这种情况下

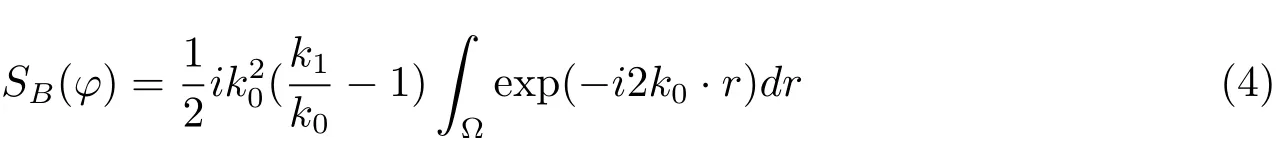
表示散射振幅和δB的Born近似[30−32].与SB相比,Born近似导致的误差是很小的.

为了求方程(4)的导数近似,首先利用方程(1)和辐射边界条件下区域ψ中边界Γ的光滑性,得到格林函数表示为

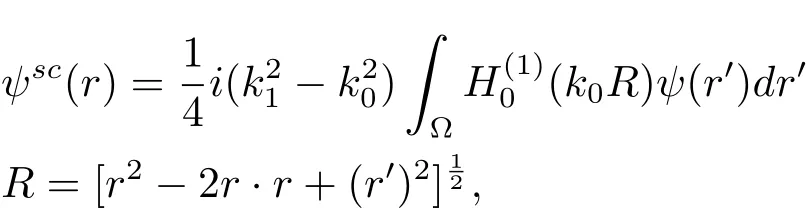
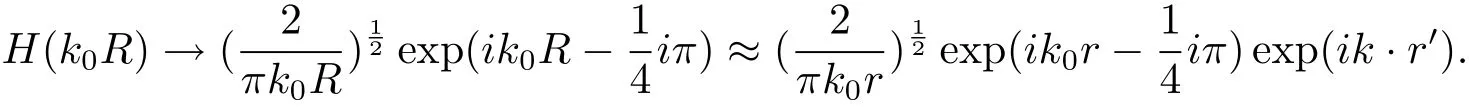
对于模型的离散测量数据,考虑

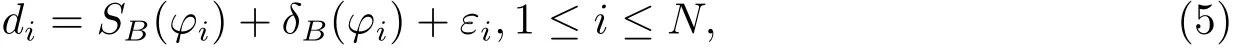
其中εi表示噪声.假设εi是随机变量,满足

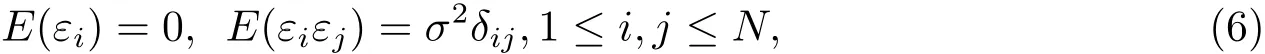
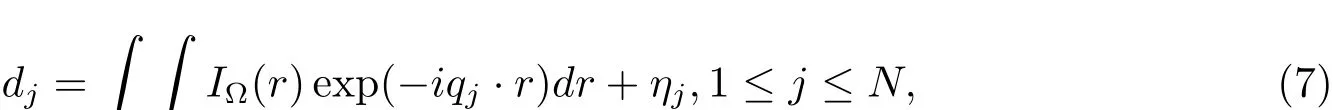
其中如果r∈Ω(0除外),则IΩ(r)=1.q用极坐标表示为(2k0,ϕ),Born近似所导致的误差包含在ηj中.

为了解决反问题的数据缺失和不适定性,使问题更容易处理,对问题进行降维处理.假设散射区域Ω呈星形,方程(7)转化为极坐标表示

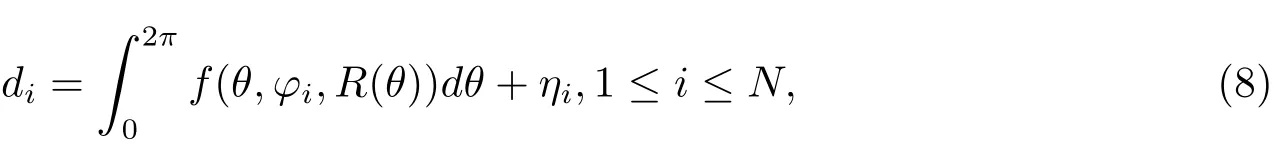
其中

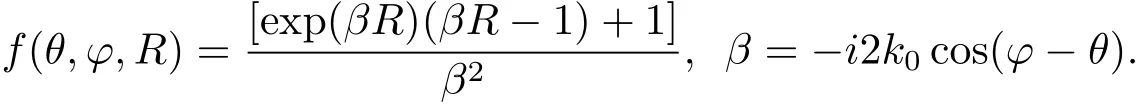
方程(8)可以转化为一维非线性第一类Fredholm积分方程

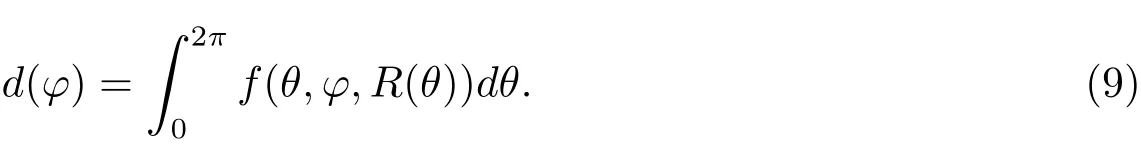
一般来说,该方程的解R(θ)不连续依赖于数据d(ϕ).

3 迭代正则化Gauss-Newton法

方程(9)可以归结为求解非线性方程F(γ)=y,这里

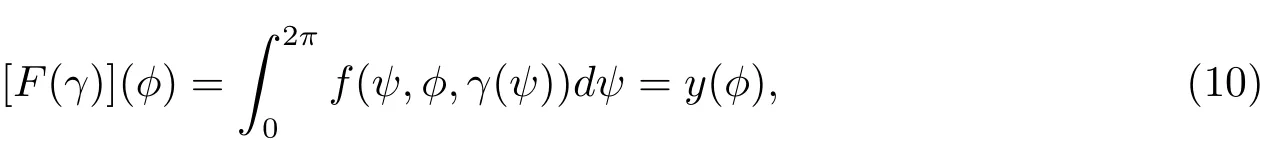
其中

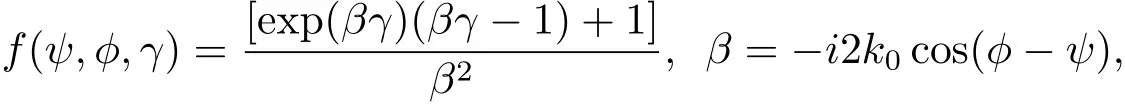
k0是固定波数,γ(ψ)未知[1,2,33].

在实际问题中,右端数据y通常是由测量得到的,因而得到的数据是一个满足kyδ−yk≤δ的近似数据yδ,这里δ>0是给定的较小的扰动水平[34−35].

求解不适定问题的方法主要有两种:Tikhonov正则化和迭代法,本文主要采用迭代正则化Gauss-Newton法求解逆散射问题.

定义泛函

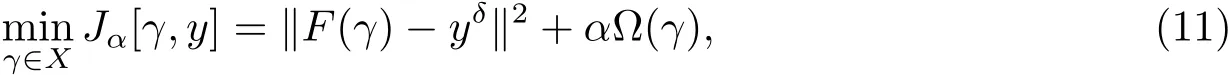
其中α>0为正则化参数,Ω(γ)为稳定泛函.要求无约束最优化问题(11)的解,首先将算子F线性化,利用F(γ)在第k次迭代点γk处的泰勒展开式,得到

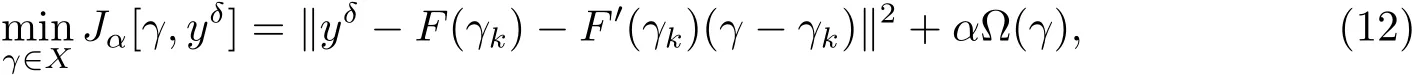
其中Ω(γ)=kL(γ−γ0)k为稳定泛函,L是单位矩阵(L=L0=I∈Rn×n)或者是一阶或二阶导算子的离散近似,即

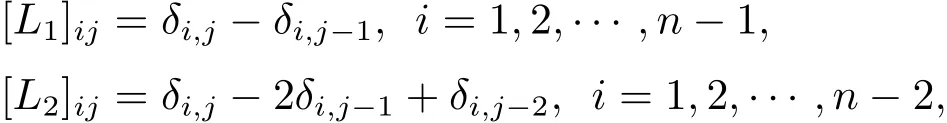
其中δij为克罗内克符号,j=1,2,···,n.方程(12)通过一阶最优条件求解,可得到

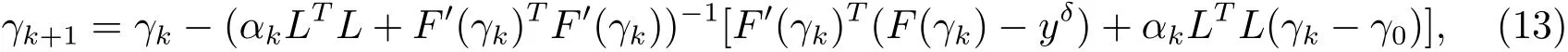
(13)式称为迭代正则化Gauss-Newton法[36−37],简记为IRGN法.

要利用此方法数值求解逆散射问题(10),需要将其离散化,本文采用梯形公式将其离散.将公式(13)改写为如下形式

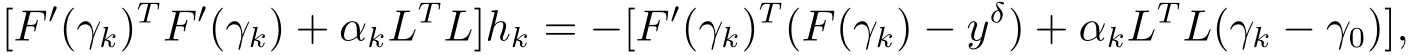
其中hk=γk+1−γk,要得到F0(γk)TF0(γk),需要求解非线性算子F 的Fr´echet导数.

边坡工程按持久工况(天然工况)和短暂工况(暴雨工况)两种工况利用理正软件进行计算设计。本次稳定计算及边坡设计安全系数具体取值为表2。

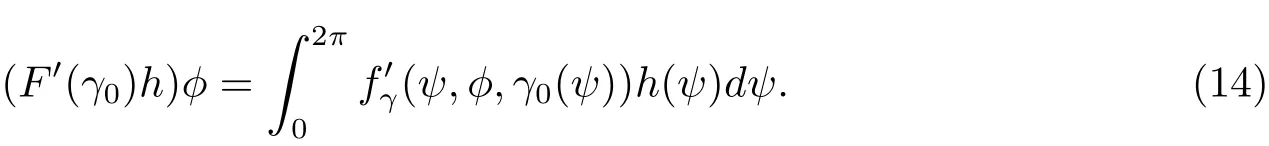
上述(14)式定义的算子是[0,2π]上的线性连续算子.

事实上,对于确定的θ=θ(h)∈[0,1],有

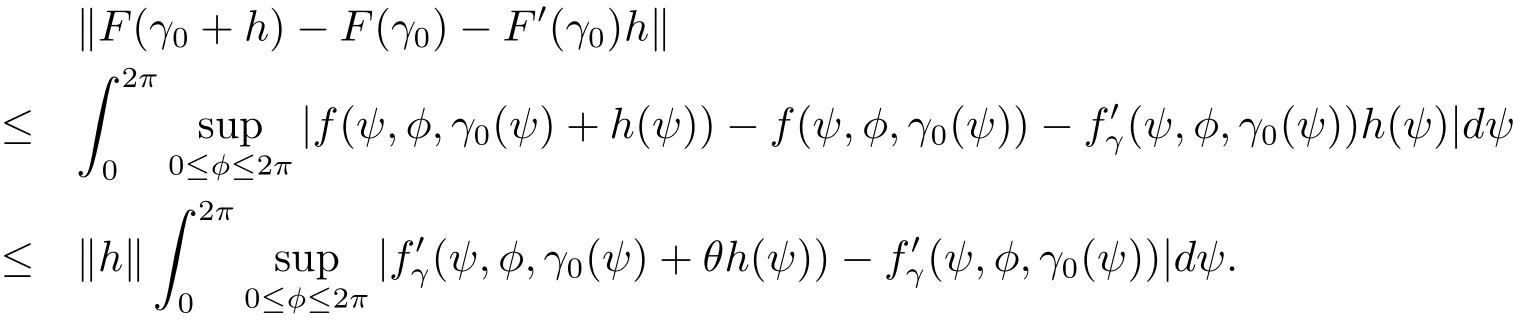
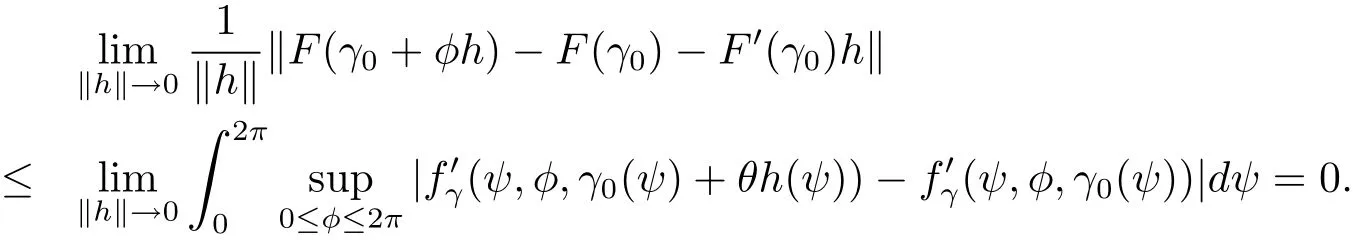
因此F 的Fr´echet导数可以通过(14)式得到.

利用梯形公式将方程(14)进行离散:把区间[0,2π]等分成N 个小区间,其步长为同理 ψ0= φ0=0,ψN= φN=2π,φj=j4s(ψj= φj).设 γ(ψj)= γj,则有

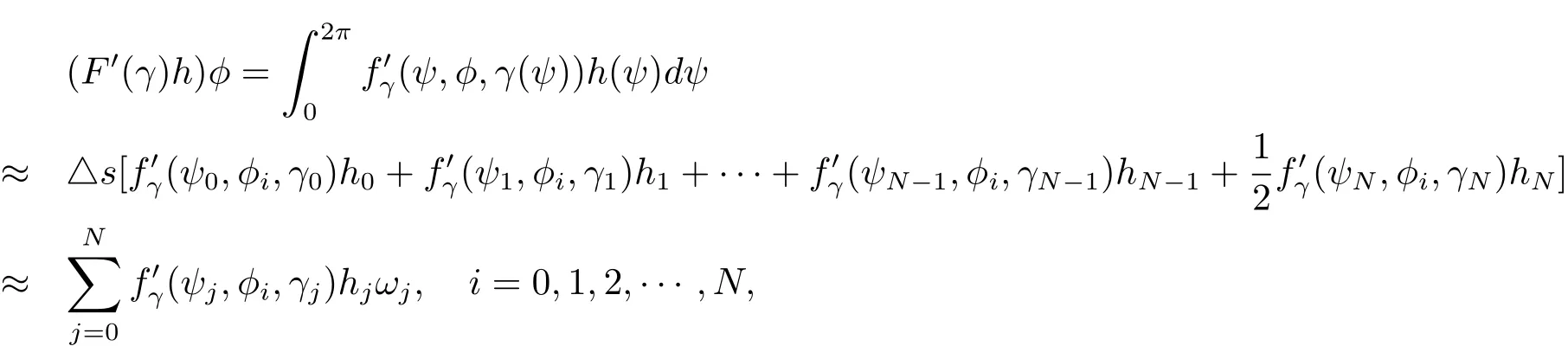
改写成矩阵形式为

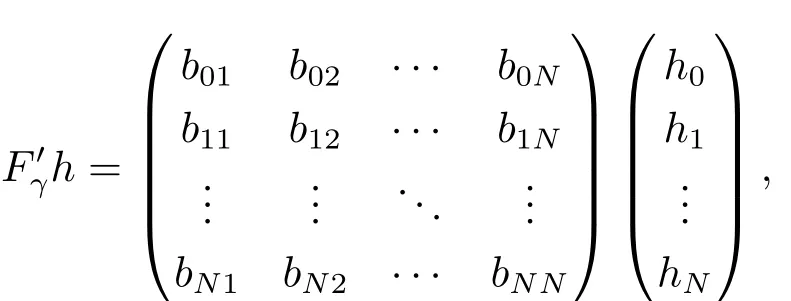
其中

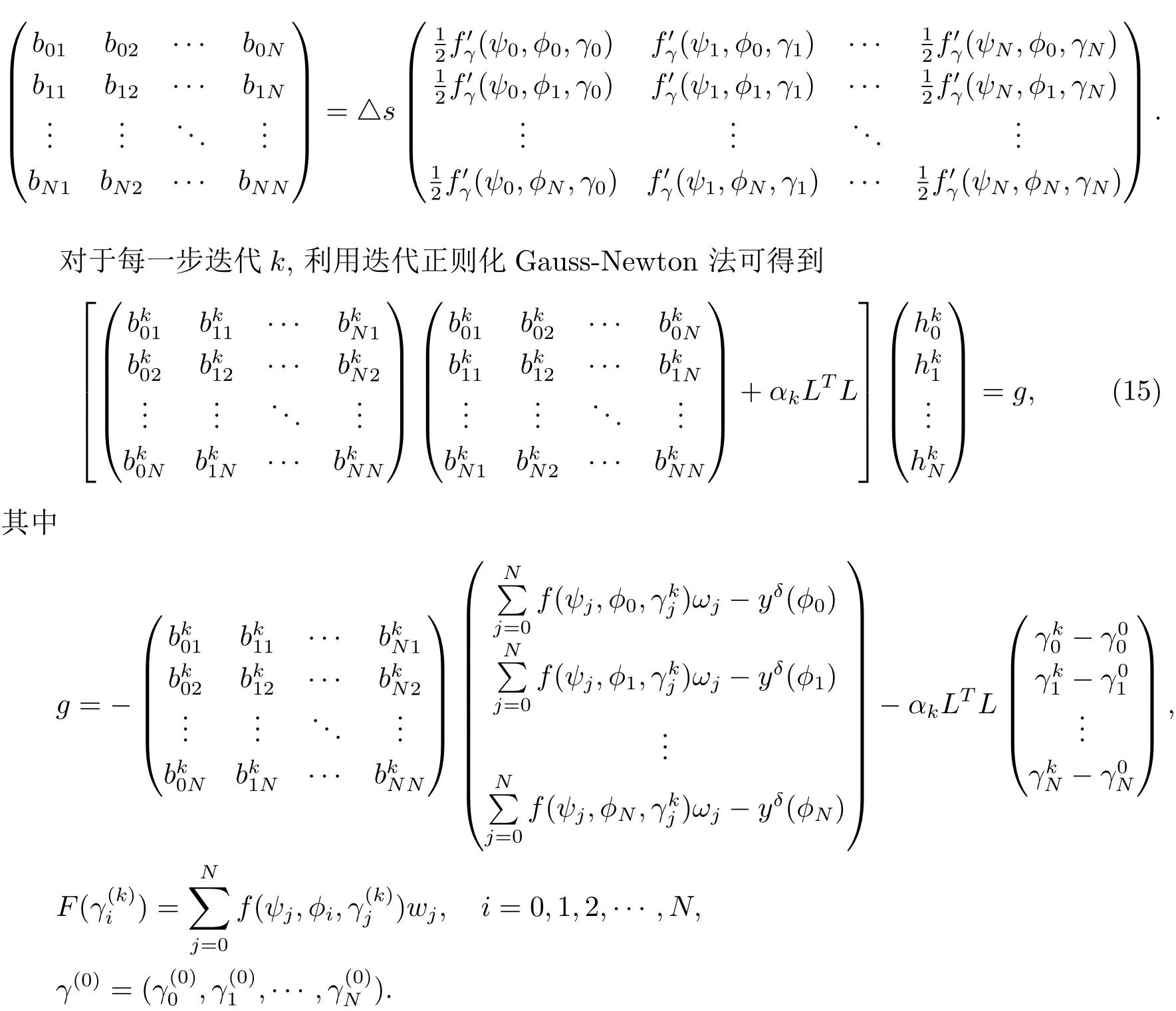
因此得到迭代格式γ(k+1)=γ(k)+h(k),通过此格式便可求出方程(10)的近似解.

4 数值模拟

考虑方程(10)所示的逆散射问题,在数值求解之前 ,先做如下规定fl其中ψj为节点,N为区间[0,2π]上均匀分布的节点的个数,γ(ψ)为精确解,∼γ(ψ)为数值解.

(3)在数值计算时,假定扰动{yδ(φj)}Nj=0是随机的,但是在实际应用时,反复测试是相当困难甚至不可能的.因此,考虑确定性误差.假设观测到的数据有以下扰动形式

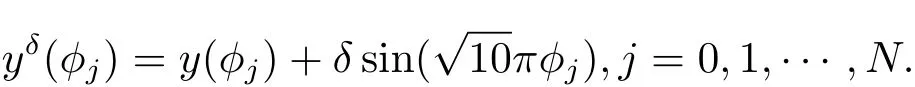
(4)基于Sigmoid-型函数的性质,选取正则化参数为

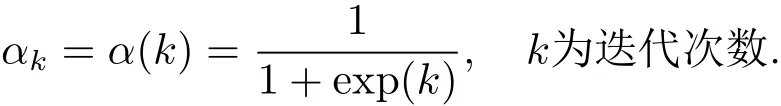
不难验证其满足下列条件

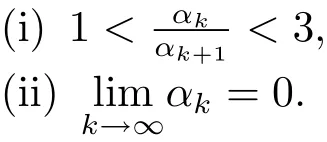
可以看到,根据上述正则化参数的选取方法,在迭代开始时能够充分对问题进行正则化,然后随着迭代数的增加正则化参数逐渐减小,达到解稳定的目的.

数值模拟时,对所要识别的障碍物边界γ(ψ),给定两种参数化模型的精确解,分别对所得数值解和精确解进行比较,以验证本文所提方法的有效性.

数值模拟一考虑真解

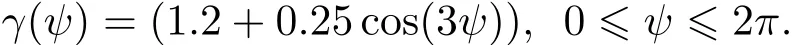
数值模拟时,取N=100,L=L1,k0=2,迭代次数k=30,初始猜测γ(0)=(1,1,···,1)T,扰动分别为δ=0,0.01,0.05时,所得L∞和RE分别如表1所示,精确解与数值解的比较如图1所示.

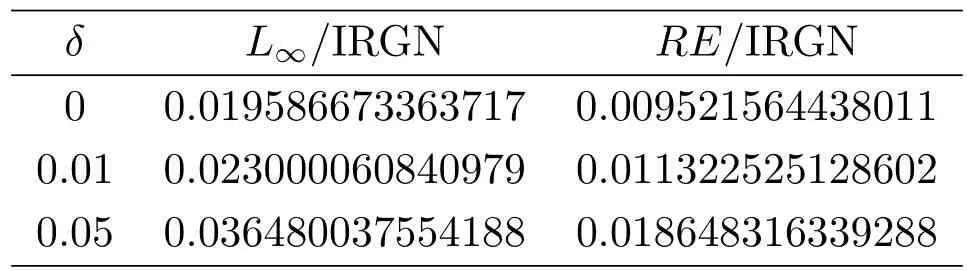
表1 :不同扰动、相同迭代数下,迭代正则化Gauss-Newton法所得误差比较

取N=100,k0=2,迭代次数k=30,初始猜测γ(0)=(1,1,···,1)T,L分别取单位矩阵I、L1或L2,扰动分别为δ=0,0.01,0.05时,所得L∞和RE分别如表2、表3所示,精确解与数值解的比较如图2所示.

表2 :不同扰动、相同迭代数下,L取不同时所得误差(L∞)比较

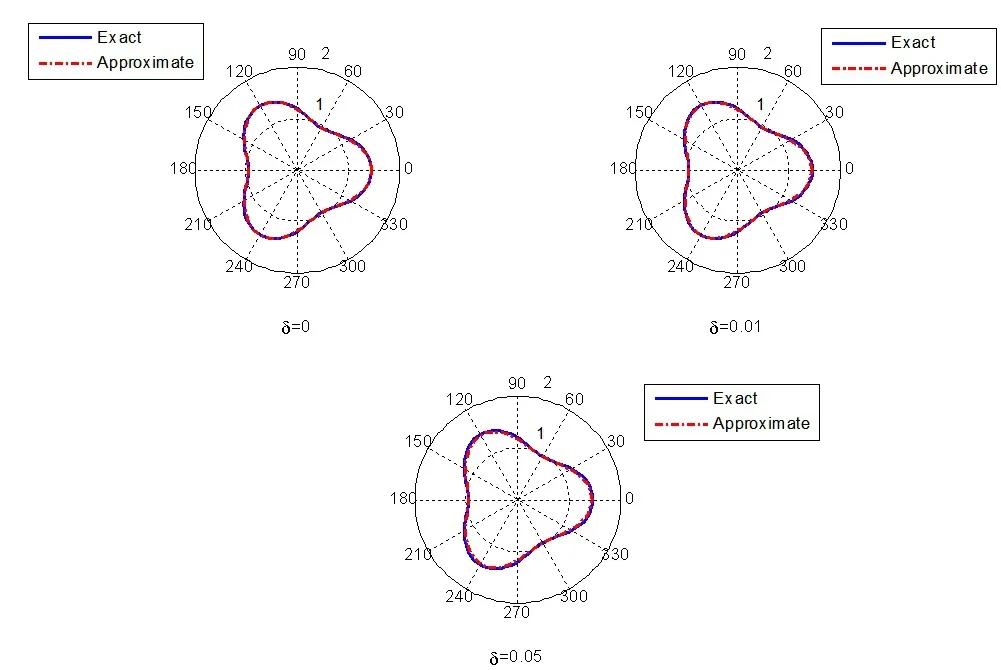
图1 :取不同的扰动水平δ时,所得精确解与数值解的比较

表3 :不同扰动、相同迭代数下,L取不同时所得误差(RE)比较

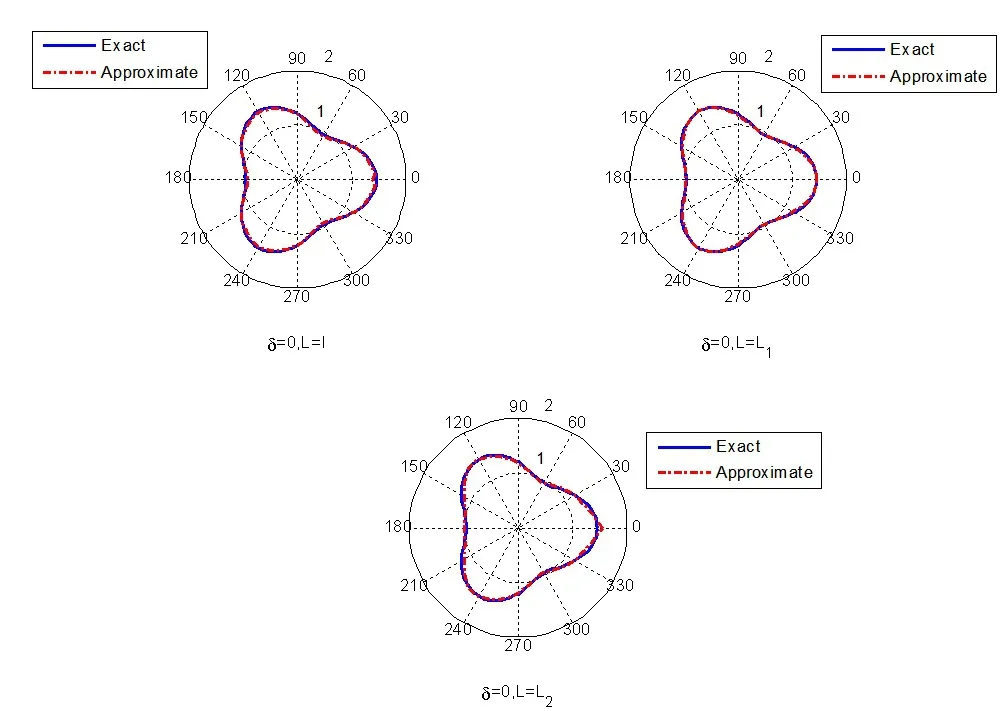
图2 :无扰动时,L取不同的值所得精确解与数值解的比较

数值模拟二考虑真解

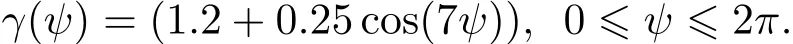
参数设置与模拟一相同,所得L∞和RE分别如下表4所示,精确解与数值解的比较如图3所示.

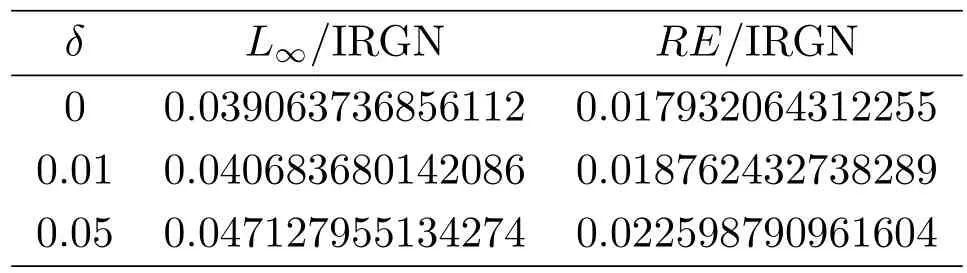
表4 :不同扰动、相同迭代数下,迭代正则化Gauss-Newton法所得误差比较

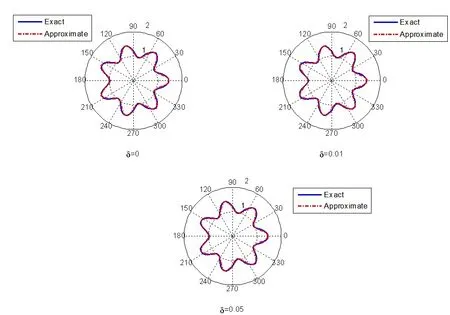
图3 :取不同的扰动水平δ时,所得精确解与数值解的比较

取N=100,k0=2,迭代次数k=30,初始猜测γ(0)=(1,1,···,1)T,L分别取单位矩阵I、L1或L2,扰动分别为δ=0,0.01,0.05时,所得L∞和RE分别如下表5、表6所示,精确解与数值解的比较如下图4所示.

表5 :不同扰动、相同迭代数下,L取不同时所得误差L∞比较

表6 :不同扰动、相同迭代数下,L取不同时所得误差RE比较

比较上述两个数值模拟结果,可以得到如下结论:从表1和表4可以看出,在迭代数相同的情况下,当右端测量数据无扰动时,所得解的误差很小,数值解较准确,而随着扰动的增加,数值解与精确解误差的∞-范数和相对误差也逐渐增加;从表2、表3和表5、表6可以看出,在迭代数一定的情况下,取不同的L值时,随着扰动的增加,所得数值解与精确解误差的∞-范数和相对误差都在非常小的范围内,特别取L=L1时,所得数值解与精确解误差的∞-范数和相对误差都相对较小.

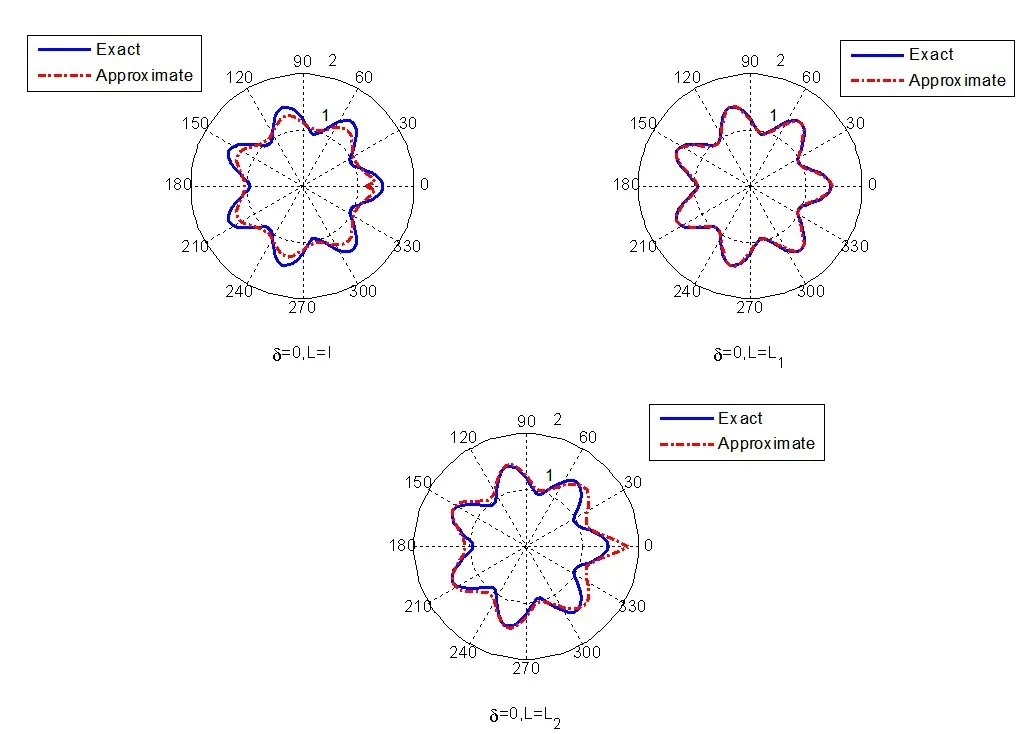
图4 :无扰动时,L取不同的值所得精确解与数值解的比较

5 结论

本文采用迭代正则化Gauss-Newton法求解一类根据远场散射数据识别介质中障碍物形状的逆散射问题,通过数值模拟可以看出:用此方法求解此类问题是可行的、有效的;但是对于参数化后的边界函数,在利用正则化方法求解时,当稳定泛函中的L取不同的算子时,数值解的稳定性和准确性有微小差别,而当L取一阶导算子时,数值求解所得结果更准确.