一个三次等时中心在非光滑扰动下的极限环分支

宋海风,彭临平,2

(1.北京航空航天大学数学与系统科学学院,北京 100191)

(2.北京航空航天大学数学、信息与行为教育部重点实验室,北京 100191)

1 引言

众所周知,研究多项式微分系统的极限环个数是实平面微分系统定性理论的重要部分之一,这类问题的主要研究方法有逆积分因子法,Abelian积分法及平均方法等.对于光滑系统的极限环个数,已经得到了很多重要结论[1−10].

由于非光滑现象广泛存在于自然科学和工程技术等领域,近年来非光滑系统越来越被重视,特别是关于非光滑系统极限环分支的研究工作更是层出不穷,其中有两个重要的工作要特别指出:Liu和Han研究了平面分段光滑的Hamilton系统的闭轨族的极限环分支问题,推导证明了分段光滑系统的一阶Melnikov函数计算公式[11];Llibre等介绍了不连续系统的平均理论,给出了平均函数的表达式[12].又如Liang和Han利用Melnikov方法,研究了擦边闭轨内外两侧闭轨族分支出的极限环的最大个数,给出了广义同宿分支的条件及二重广义分支的条件[13].Li和Liu研究了分段光滑二次微分系统的闭轨族的极限环分支问题,借助于不连续微分系统的平均理论和复方法,估计了所考虑的系统在n次扰动下分支产生的极限环的最大个数[14].Cen等利用一阶平均方法及Chebyshev准则,研究了一类二次等时中心在分段光滑的二次多项式扰动下的极限环分支现象,给出了分支产生的极限环的最大个数[15].

本文选取了如下三次可积非Hamilton系统

显然,系统(1.1)有首次积分

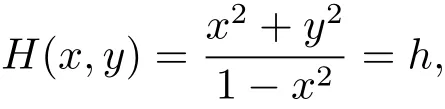
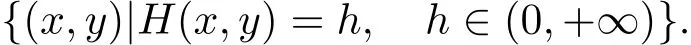
系统(1.1)的相图如图1所示.

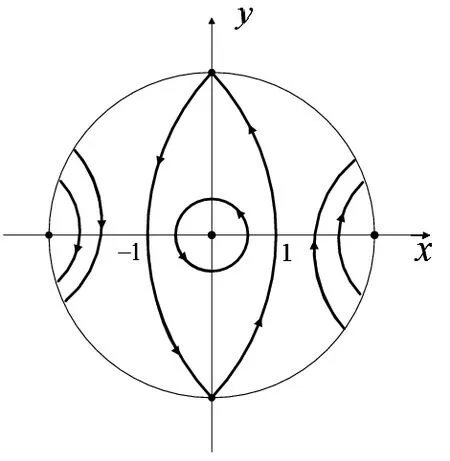
图1 :系统(1.1)的相图

利用非光滑系统的一阶平均方法,研究系统(1.1)的任意分段三次多项式小扰动即

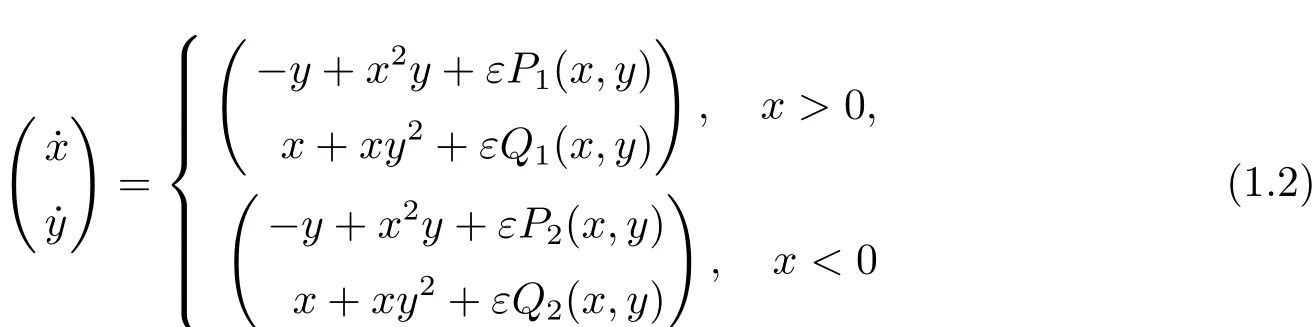
的极限环分支现象,其中0<|ε|¿1,Pi(x,y),Qi(x,y)(i=1,2)是关于变量x和y的三次多项式,表达式如下

根据系统特点,借助于一些数学技巧,证明了下述定理.

定理1.1对于三次等时中心(1.1),在任意小的分段三次多项式扰动下,从未扰系统的周期环域中至多分支出7个极限环,而且此上界是可以达到的.

注 Li和Zhao已在文献[1]中研究了系统(1.1)在光滑扰动情况下的极限环分支问题,得到的结论是最多可以从未扰动系统的周期环域中分支出3个极限环.与得到的结论相比可知,非光滑扰动比光滑扰动能分支出更多的极限环.

本文的结构安排如下:第二部分简要介绍非光滑系统的一阶平均理论；第三部分计算系统(1.2)的一阶平均函数；第四部分证明定理1.1.

2 非光滑系统的平均理论

在定理1.1的证明过程中将会用到一阶平均方法,所谓的平均方法即是将极限环的个数问题转化为研究一阶平均函数的简单零点个数.下面首先对平均理论做一个简单介绍,详细论述见文献[12,16,17].

引理2.1[12]考虑如下非光滑微分系统

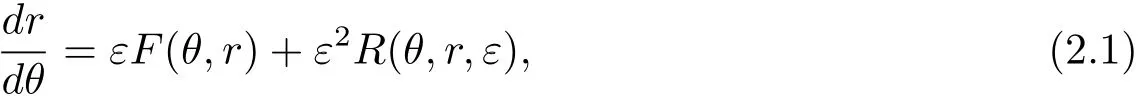
其中

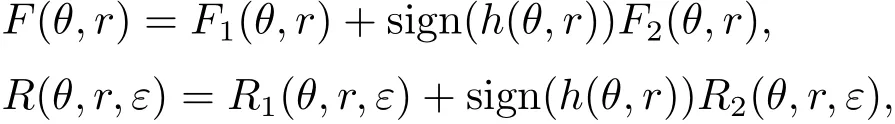
F1,F2:R×D→R,R1,R2:R×D×(−ε0,ε0)→R,h:R×D→R都是连续函数,且这些函数均是关于变量θ以T为周期的周期函数,D是R中的开子集,sign(h)是如下定义的符号函数

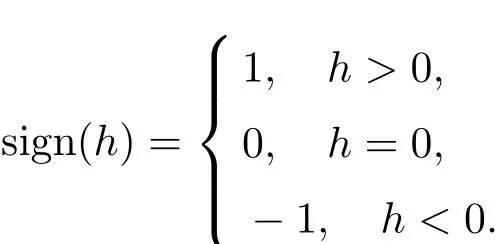
假定h(θ,r)是C1函数且0为其正则值,记M=h−1(0),Σ ={0}×D*M,Σ0=定义系统(2.1)的一阶平均函数f:D→R如下

假定系统(2.1)满足下面(i),(ii),(iii)三个条件.

(i)F1,F2,R1,R2和h关于r满足局部Lipschitz条件;

(ii)对于a∈Σ0,存在a的一个邻域V,使得对任意的z∈¯V{a},有f(z)6=0及Brouwer度函数dB(f,V,a)6=0;

为了更方便地验证引理2.1中的条件(ii),本文中我们用文献[16]中一个充分条件来代替条件(ii).

注2.1假定f:D→R是C1函数且f(a)=0,其中D是R中的开子集且a∈D.如果雅克比行列式Jf(a)6=0时,存在a的一个邻域V使得对所有的有

考虑如下形式的平面微分系统

其中P(x,y),Q(x,y),p(x,y),q(x,y):R2→R是连续函数,ε是小参数.假设系统(2.3)|ε=0围绕中心(0,0)的周期环域

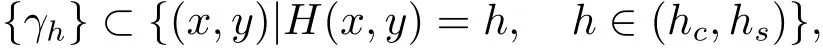
其中H(x,y)=h是系统(2.3)|ε=0的一个首次积分,hc和hs分别对应中心和分界线处的Hamilton函数值.

引理2.2[16]考虑系统(2.3)|ε=0及其首次积分H(x,y)=h.假设对于周期环域中的所有(x,y),都有xQ(x,y)−yP(x,y)60成立.设是一个连续函数,并且对所有的和θ∈ [0,2π)都有

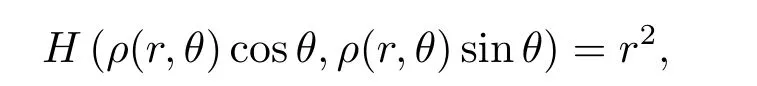
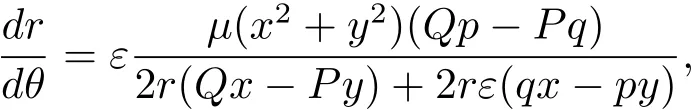
其中µ=µ(x,y)是系统(2.3)|ε=0相应于首次积分H(x,y)=h的积分因子,x=ρ(r,θ)cosθ,y= ρ(r,θ)sinθ.P,Q,p 和q 同前.

3 平均函数的计算

对于系统(1.1)的Hamilton函数

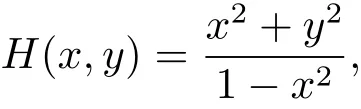
选择如下的函数

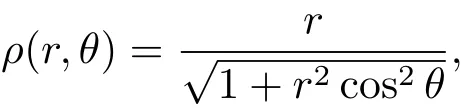
使得

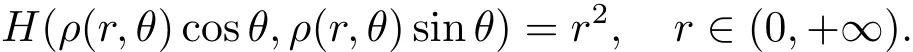
对系统(1.2)做变换

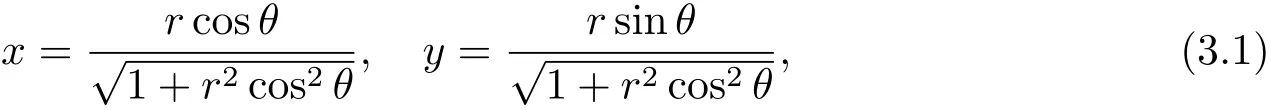
则有

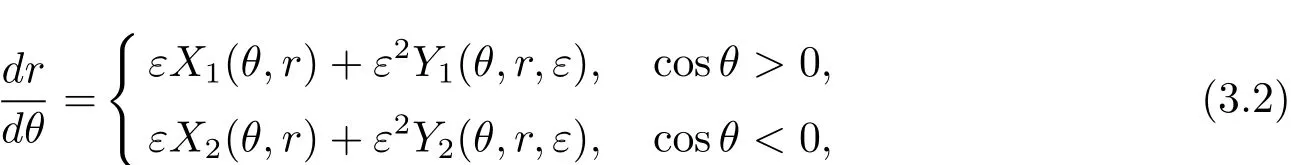
其中

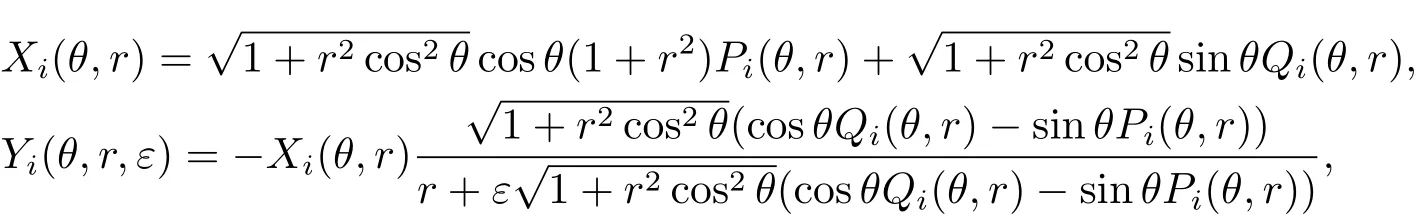
这里Pi(θ,r)和Qi(θ,r)是(1.2)式中的Pi(x,y),Qi(x,y)(i=1,2)通过(3.1)式变换得到的.令

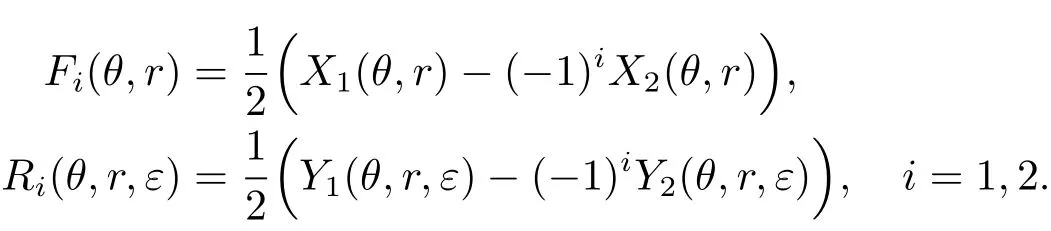
则系统(3.2)可以写成以下标准形式

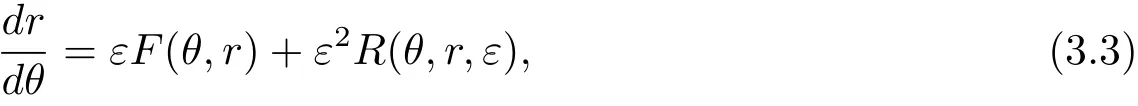
其中

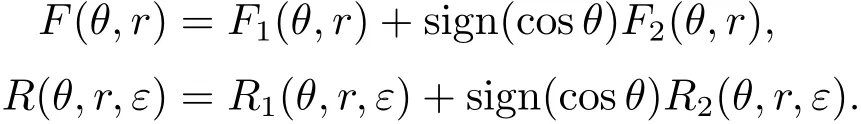
易验证方程(3.3)满足引理2.1中的三个条件,其一阶平均函数为

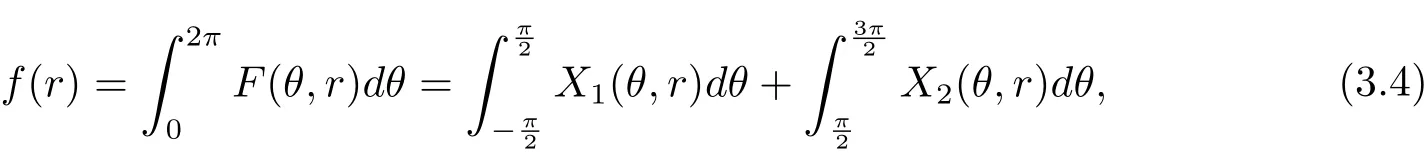
对上式中第二个积分做变量替换θ→π−θ,则(3.4)式转化为

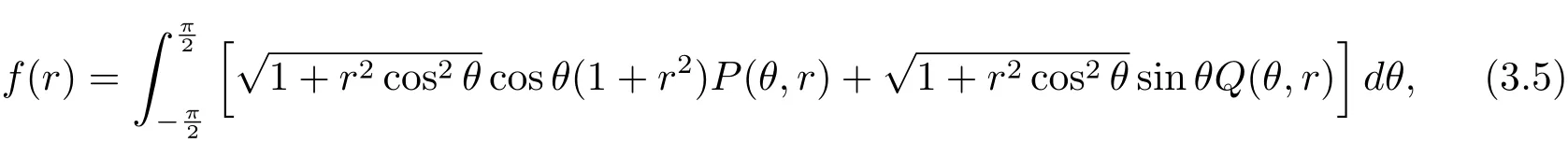
其中

直接计算可得下列结论.

引理3.1以下积分等式成立

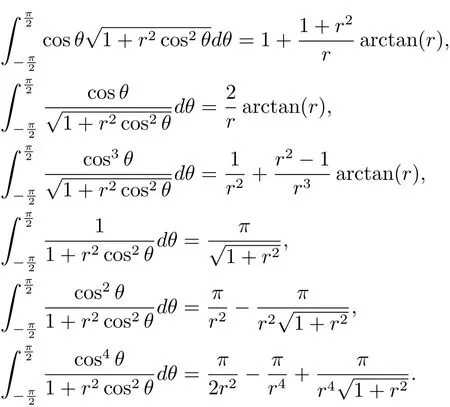
将引理3.1代入(3.5)式整理得

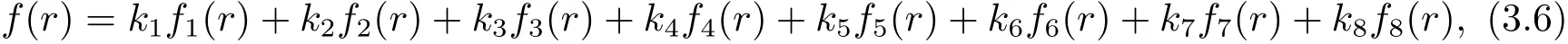
其中

且

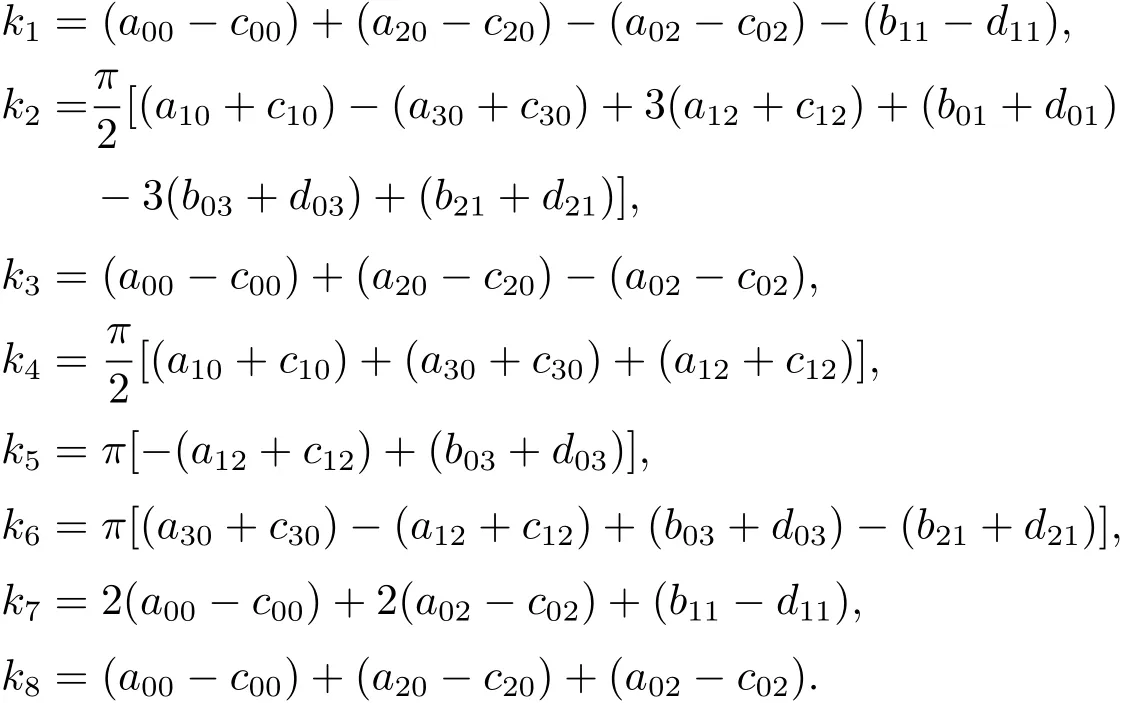
命题3.1式(3.6)中的8个函数fi:(0,+∞)→R(i=1,2,3,4,5,6,7,8)是线性无关的且系数k1,k2,···,k8关于扰动参数是相互独立的.

证 易知函数fi:(0,+∞)→R(i=1,2,3,4,5,6,7,8)在r=0处的泰勒展开式分别为

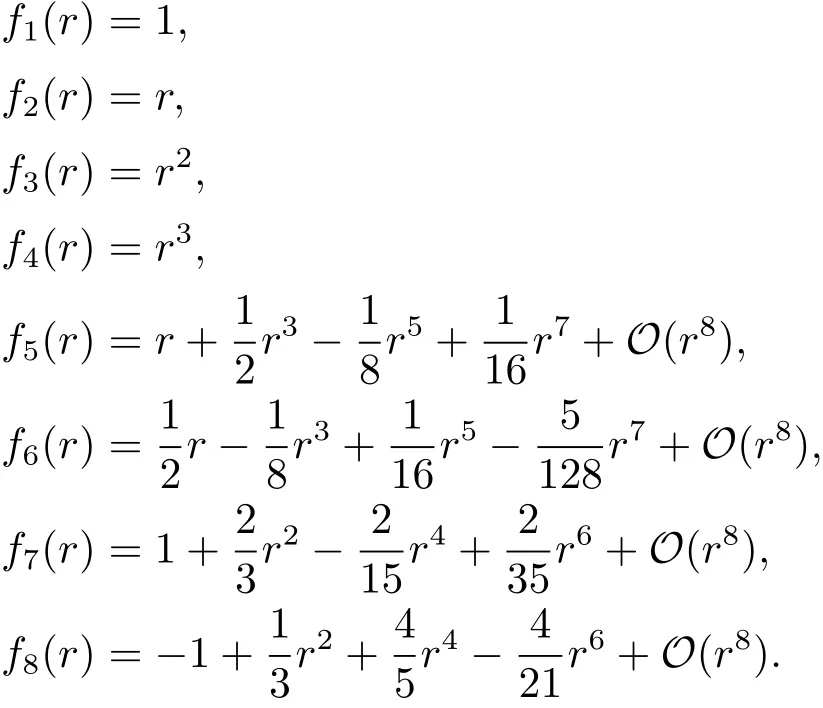
通过计算可以得到

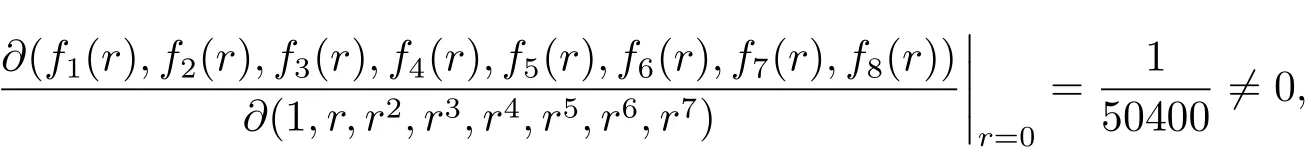
所以这些函数是线性无关的.进一步有

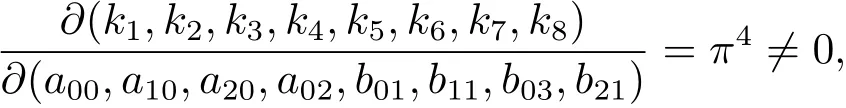
由此可知系数k1,k2,···,k8关于扰动参数是相互独立的.

4 主要结果的证明

这一部分主要研究f(r)的零点个数,为此介绍一个重要的引理.

引理4.1[2]考虑n个线性无关的解析函数hi(x):D→R,i=1,2,···,n,其中D⊂R是一个区间.假设存在k∈{1,2,···,n}使得hk(x)在D 上不变号,则一定存在n个常数ci(i=1,2,···,n) 使得在D上至少有n−1个简单零点.

由此引理及命题3.1得

命题4.1函数f(r)在区间(0,+∞)上零点个数的最大值至少为7.

定理1.1的证明为了估计f(r)在r∈(0,+∞)上零点个数的最小上界,令F(r)=rf(r).显然F(r)和f(r)在r∈(0,+∞)上有完全相同的零点个数.进一步有

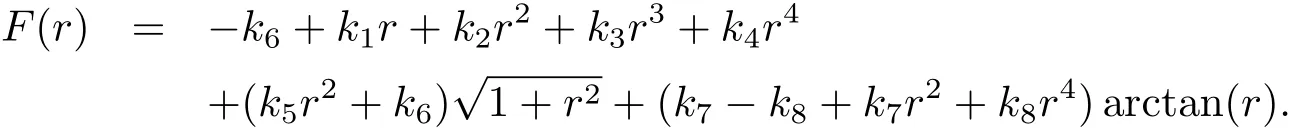
对F(r)求五阶导得

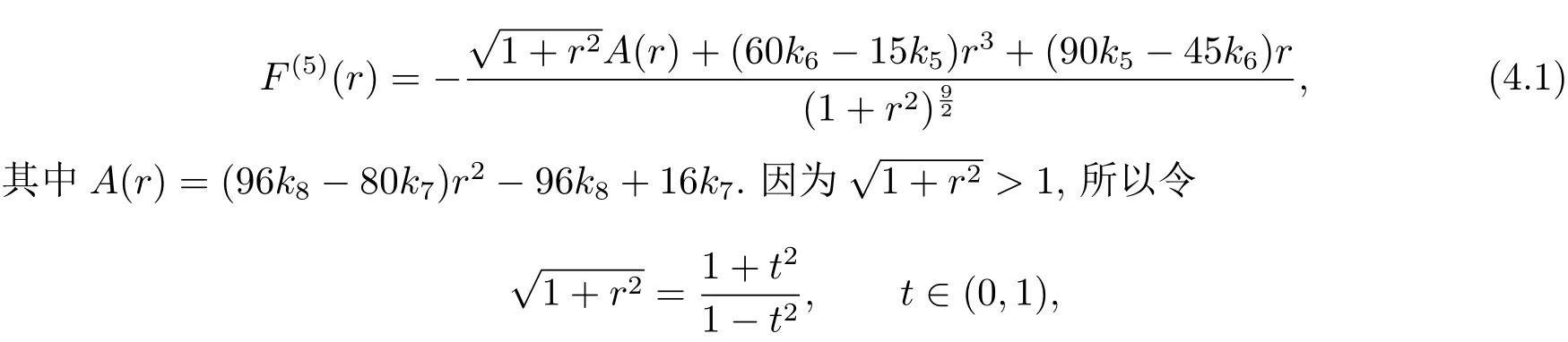
那么

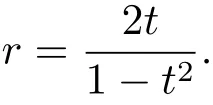
则函数(4.1)变为

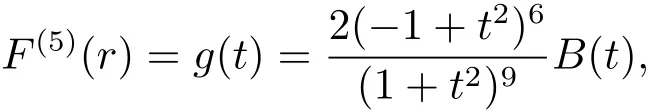
其中

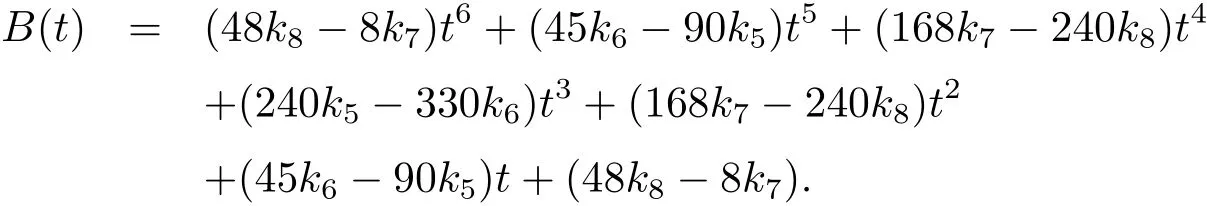
由于多项式B(t)的系数是对称的,若t06=0是其零点的话,则1/t0也为其零点,所以g(t)在(0,1)上至多有3个零点,即F(5)(r)在(0,+∞)上至多有3个零点,从而F(r)在[0,+∞)上至多有8个零点.由于F(0)≡0,所以F(r)在(0,+∞)上至多有7个零点,由其定义知函数f(r)在(0,+∞)至多有7个零点.再根据命题4.1得f(r)零点个数的最大值为7.

根据引理2.1,系统(1.2)至多有7个极限环从未扰动系统的周期环域中分支出来,而且最大个数7是可以达到的.定理1.1得证.