巧用数形结合 锻造初中生数学核心素养
林露


【摘 要】数学是思维的殿堂,数形结合则是数学与思维搭建的桥梁。数形结合可以使学生建立起数与形之间的关系,在学习数形结合的过程中,能够培养学生的直观想象能力、逻辑推理能力、数学运算能力以及数学抽象能力。在传统教学中,教师往往只将数形结合作为解题工具,而未将其作为提升学生数学素养的方法,忽略了这项思想对学生的重要性。
【关键词】数形结合;初中数学;核心素养
初中数学中有许多思想需要学生掌握,数形结合就是其中的重要思想之一。数形结合是通过建立起数形之间的联系,利用形帮助学生更好地理解数,通过数理清形的规律,从而使学生掌握解决数学问题的方法。巧用数形结合进行教学,不仅可以开发学生的思维空间,还能够有效培养初中生的数学核心素养。
一、数形结合对锻造初中生数学核心素养的重要性
数学结合是初中数学中最基本的思想方法之一。数可以解答形的基本性质,而形可以表达数的特征,数与形的结合能够将数学问题的性质与特征都展现出来。学生在解答数学题目时,难以直接通过题目把握到数的变化,特别对于一些由几个函数组成的题型,学生往往不知从何下手。借助数形结合思想,学生则能通过形观察到数的特征,从而找到解答问题的方法。数形结合除了能帮助学生解决问题,还可以让学生理解数学、掌握数学,从数学本质中提升自己的数学素养。在学习一些新的函数或图形时,数形结合可以让学生了解数形之间的内在关系,从而提高解题效率、提高教学效率。教师应积极运用数形结合,让学生更好地从数学题目中汲取到更多数学知识,感受到学习数学的乐趣,从而锻造学生的数学核心素养。
二、巧用数形结合锻造初中生数学核心素养的策略
1.利用数形结合,培养学生的逻辑推理素养
数形结合思想不僅可以将数变成形,还可以将形变成数进行解答,通过逻辑推理的方式,解答用图形难以表达的问题。在解答几何类型题目时,可以通过将几何问题转化成代数问题,从数量关系的方向解决几何问题中的逻辑问题。
如例题一:如图一所示,在△AOB中,A点的坐标为(2,4),B点的坐标为(6,2),求△AOB的面积。
这道题考察的是学生对坐标与图形面积的掌握程度,在解答这道题目时,学生还没有掌握求出这个三角形高的计算方法,因此无法通过三角形的面积公式直接算出面积。但通过观察图形,我们可以将需要求出的三角形与周围可以求出的三角形进行组合,形成一个可以求出的矩形,然后用矩形面积减去周围面积可以求出的三角形面积,就能得出中间未知的△AOB的面积。
分别过点A,B做y,x轴的垂线,垂足为C、E,交点为D,则有:
在这道题目中,通过数形结合的思想,依据题目中的逻辑关系,将几何题目转化成了代数题目,简答地证明了这道几何问题。在学生需要完成一些逻辑推理题目时,其中的关系有时很难用几何方式表述,通过数形结合,可以将这些逻辑关系转化成代数题目,通过计算的方式,理清几何题目中的逻辑关系,从而在计算过程中培养学生的逻辑推理素养。
2.巧用数形结合,培养学生的数学运算素养
在初中数学中,函数的运算是学生感到最难的地方,许多学生在计算函数的过程中,往往是通过小学那般通过计算的方式得出结果,这样的计算不仅复杂,而且不容易发现解题的方法。通过数形结合的方法,可以利用函数图像帮助学生快速找出解题方向,提升学生的数学运算素养。
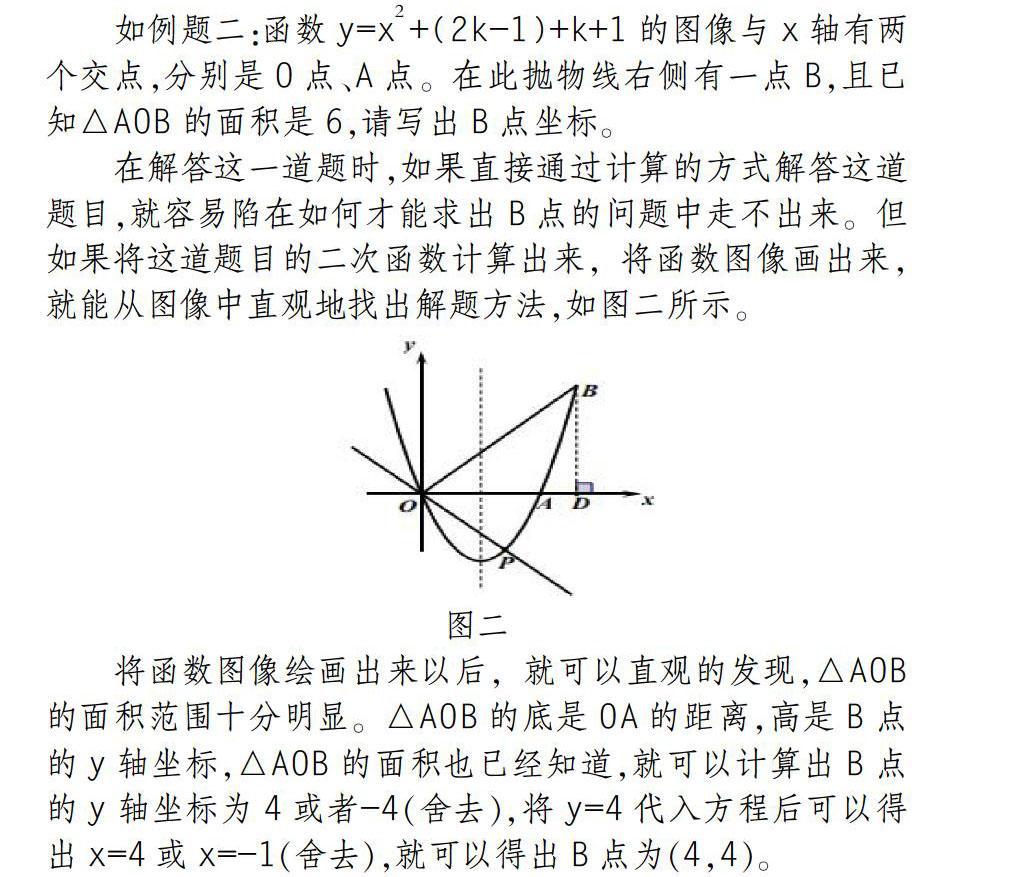
在解答这一道题时,如果直接通过计算的方式解答这道题目,就容易陷在如何才能求出B点的问题中走不出来。但如果将这道题目的二次函数计算出来,将函数图像画出来,就能从图像中直观地找出解题方法,如图二所示。
将函数图像绘画出来以后,就可以直观的发现,△AOB的面积范围十分明显。△AOB的底是OA的距离,高是B点的y轴坐标,△AOB的面积也已经知道,就可以计算出B点的y轴坐标为4或者-4(舍去),将y=4代入方程后可以得出x=4或x=-1(舍去),就可以得出B点为(4,4)。
在计算这样的函数题目时,直接对函数进行计算是不容易找到解题方向的,而将函数图像画出来,就可以在图形中找到解题思路,获得计算方法。
3.妙用数形结合,培养学生的直观想象素养
在初中数学中,不等式是学生学习较为吃力的一个知识点,复杂的解集让学生找不到方向。教师通过应用数形结合,可以让学生以更加直观的方式分析不等式的几何意义,找到不等式的解题方式。
如例题三:
在解答不等式组时,解集需要同时满足不等式组中的所有不等式解集,学生在解答这样题目时,经常会将解集的公共部分弄混,导致答案中遗漏或者多了部分解集。但在不等式的解答中运用数形结合,能将抽象的不等式解集转变成可以直接观察的图形,方便学生解答。
通过数形结合的方式,我们可以将不等式组中的每一个解集都转化成图形当中的一部分,通过图形的方式清晰地看到不等式组在数轴上的共同部分,从而得出不等式组的解集为-1≤x≤3。数形结合的方式在面对一节较为复杂的不等式组时,能够帮助学生理清不等式解集。在数学教学中,教师通过运用数形结合的方式,将问题转化为图形,可以让学生从图形中直接感受这类问题的特点,从而理清解题思路,提升学生的直观想象素养。
三、结语
总之,数形结合是数学中应用广泛的思想,这个思想不仅是一项有效的解题方法,同样也是帮助学生理解数学的工具。教师要灵活运用数形结合思想,通过多样化的教学策略,锻造初中生的数学核心素养。
【参考文献】
[1]郑娟馥.数形结合思想在初中数学解题中的应用[J].当代教育实践与教学研究(电子刊),2018(7):424-425
[2]谢有雨.从数形结合思想切入初中数学核心素养的培养[J].考试周刊,2018(19):89
[3]毛雅琴.数形结合在初中数学教学中的运用[J].考试周刊,2019(7):83

