基于APML-FDTD的非对称平板波导模场分析

李秀明

(云南开放大学 光电与通信工程学院，云南 昆明 650500)

1 引 言

随着现代光学技术的发展，光波导的应用范围越来越广，精确分析和模拟各种不同结构的光波导器件的性能是光波导设计和研究的重要内容.时域有限差分(FDTD)法是一种非常有效的时域电磁场问题模拟计算方法[1-3]，此方法与完全匹配层(PML)吸收边界[4-5]相结合不仅可以分析目标的超宽带散射特性[6]，还可以用来模拟开域色散介质中波的传播情况[7].FDTD法与二阶Mur吸收边界条件相结合还被用于分析对称平板光波导的模场分布[8].对于非对称平板波导，文献[9]提出了弱导模式的近似渐近解，文献[10-11]用模式匹配法分别分析了膜的厚度和折射率对模场的影响.此外，Peng等人用FDTD法结合吸收边界分析了非对称共面波导的阻抗特性[12]，Zhang等人提出了一种具有肩耦合矩形腔结构的非对称等离子体波导，用FDTD法对其进行了数值模拟，研究表明：这种结构将在光学开关和传感的纳米集成器件中发挥重要的作用[13].基于非对称波导在光学集成领域中的重要用途，本文将FDTD法与各向异性完全匹配层(APML)[14-15]吸收边界相结合，分析非对称平板波导的低阶模(TE0、TE1和TE2)的模场分布，模拟模场的动态传输过程，并在此基础上分析了当衬底和芯层折射率不变，敷层折射率变化时，非对称平板波导的模场分布在芯层中的变化规律.

2 APML-FDTD离散公式

图1是平板波导的结构示意图，h为波导芯层厚度，n1、n2和n3分别为芯层、衬底和敷层的折射率.波沿y方向传播，x轴方向为折射率变化方向，由于波导结构在z方向是无限延伸，因而场量与z方向无关，该平板波导中可分别传输TE波和TM波.本文以TE波为例，对TM波也可作类似处理.

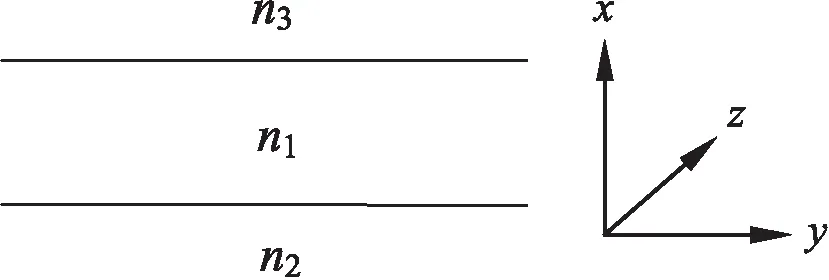
图1 非对称平板波导结构示意图

对于平板波导中传输的TE波，仅有Ez、Hx和Hy三个分量不为零，麦克斯韦方程可变形为

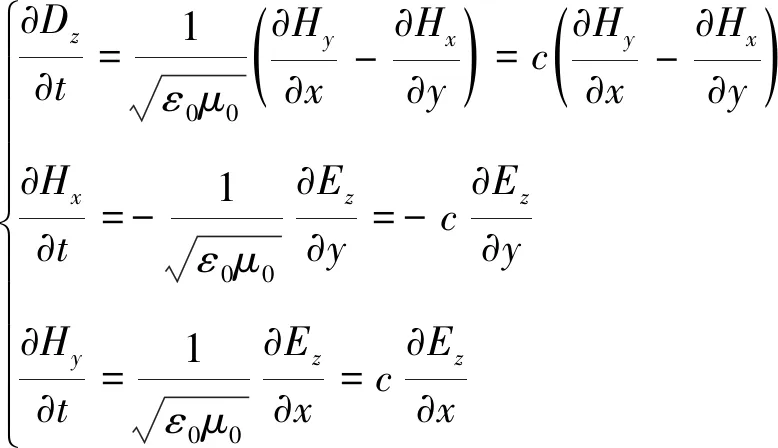
(1)

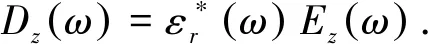
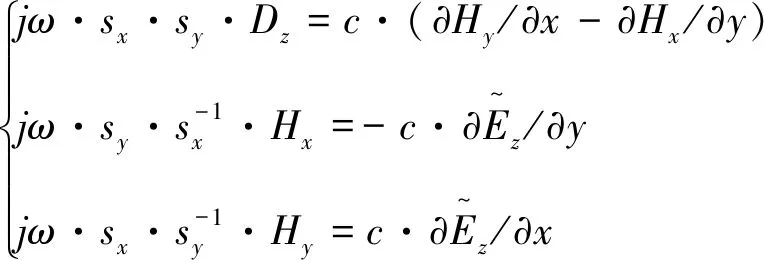
(2)

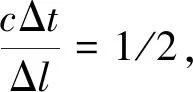
(3)

fi1(i)·IHxn+1/2(i,j+1/2)

(4)

(5)

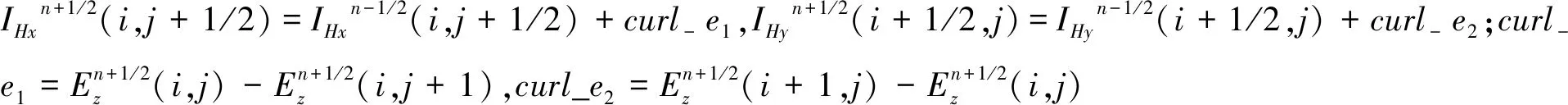
由文献[16]的数值实验结果可知，以上各式中，取σ(k)·Δt/(2ε0)=0.333×(k/length_pml)3(k=1/2,1,3/2,2,…,length_pml)

各向异性完全匹配层可获得最佳吸收效果.当计算区域位于场域而非各向异性吸收层中时，σ(k)=0,APML-FDTD离散公式(3)、(4)和(5)蜕变为场域中的FDTD差分公式.

3 数值模拟结果

选取非对称平板波导的结构参数为：h=1 μm,n1=1.6,n2=1.5,n3=1.4,传输波波长λ0=1.3 μm,基于APML-FDTD法利用matlab模拟了TE0、TE1和TE2模的场分布，结果见图2～图7.

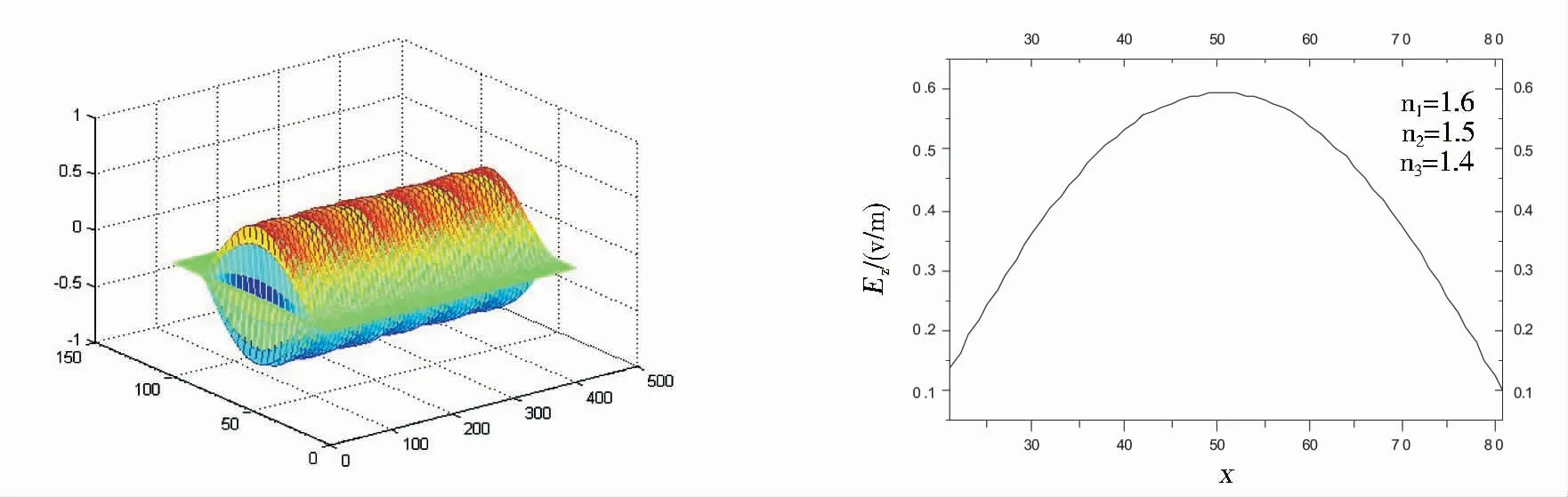
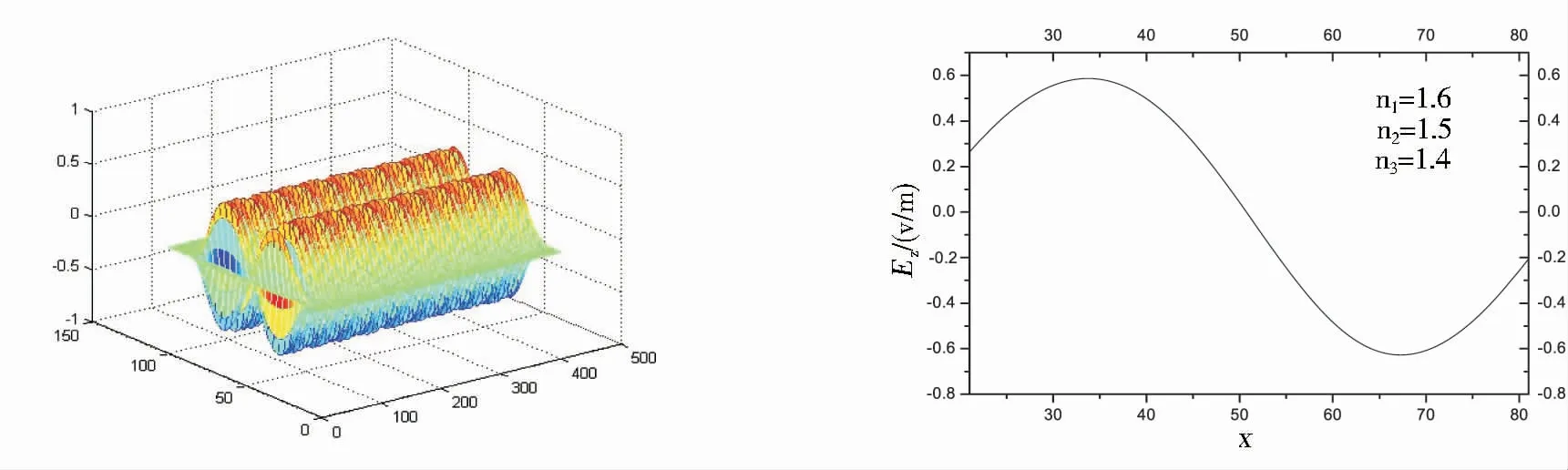
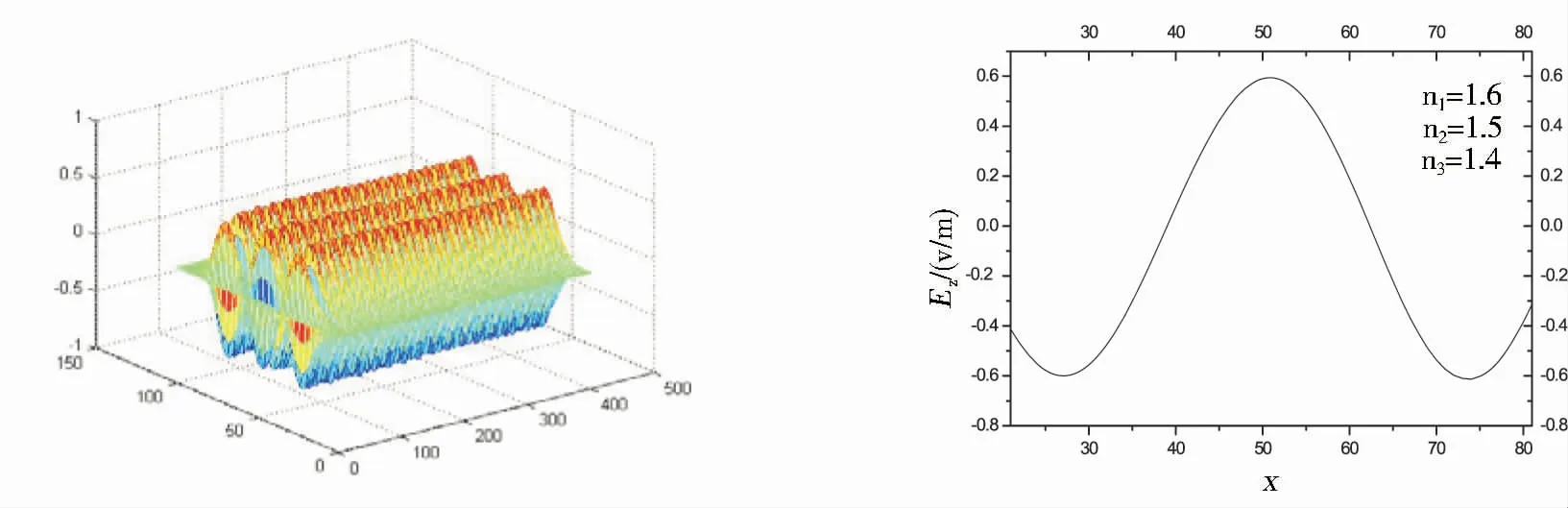
由图3、图5和图7可以看出：由于波导结构的不对称(n3略小于n2)，进入衬底(折射率较大)的能量大于进入敷层(折射率较小)的能量.

为研究模场分布与敷层折射率的关系，基于APML-FDTD法利用matlab分析了当n1和n2不变，敷层折射率n3分别等于1.2、1.3、1.4或1.5时，横向电场Ez沿x轴方向在芯层内的分布情况，结果见图8～图10.

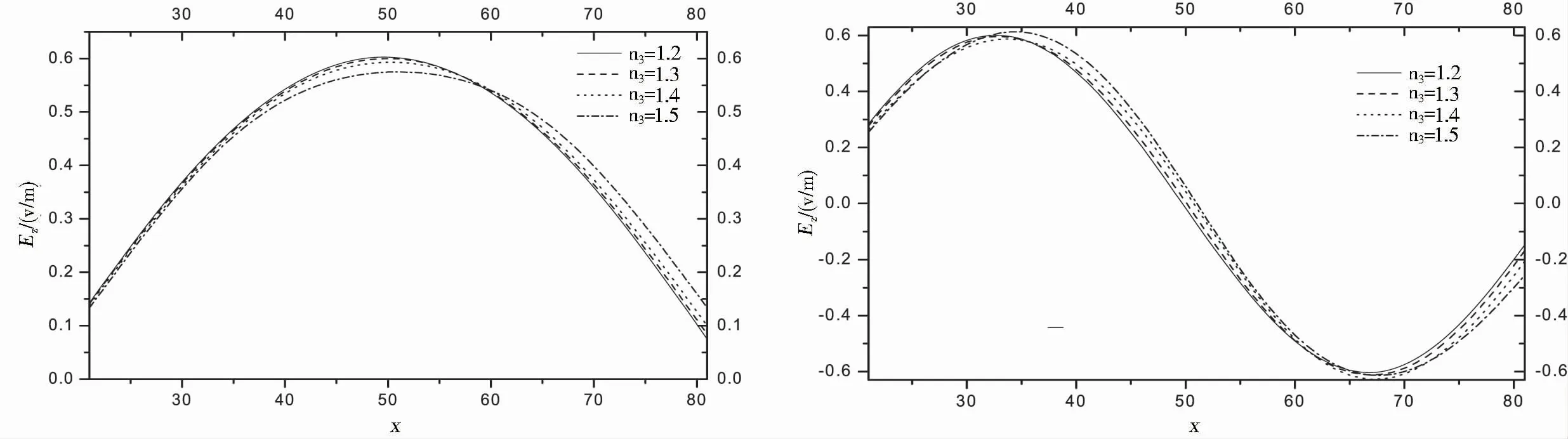
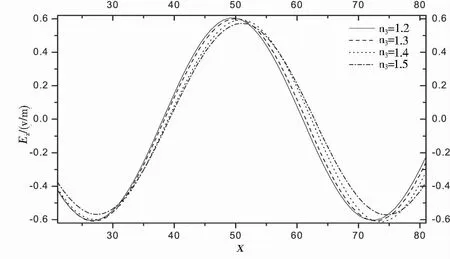
图10 Ez沿x轴方向在芯层内的分布随n3的变化(TE2)

由图8、图9和图10可以看出，三种不同模式(TE0、TE1和TE2)的场量在芯层内的分布都随敷层折射率n3的变化而变化，且都遵循这样的规律：进入敷层中的场量减小速度随着敷层折射率n3的减小越来越快，而在衬底中的场量随n3减小的变化较小.

4 结 论

利用APML-FDTD法模拟了非对称平板波导低阶模(TE0、TE1和TE2)的模场分布，比较分析了当芯层和衬底折射率不变，敷层折射率n3分别取不同值时，非对称平板波导芯层内中低阶模模场分布的变化情况.结果表明，由于波导结构的不对称(n3略小于n2)，进入衬底(折射率较大)的能量大于进入敷层(折射率较小)的能量；尽管只有n3变化，但进入衬底和敷层中的场量都受到一定的影响，且敷层折射率变化对三种模式场量分布影响的基本规律是一致的，即：进入敷层中的场量的减小速度随着敷层折射率n3的减小越来越快，而场量在衬底中减小的速度随n3减小的变化较小.这种方法模拟了整个模场的动态传输过程，分析得到的规律也为光波导器件的优化设计提供了一定的理论基础.