重叠网络上疾病与意识传播模型:非同步的影响

张译丹, 彭小龙

(1.山西大学 复杂系统研究所，山西 太原 030006；2.山西大学 数学科学学院，山西 太原 030006)

许多复杂的系统都可以抽象为一个网络.一个典型的网络由节点和连接两个节点之间的边构成,其中节点代表这个复杂系统中的个体,而边代表个体之间的相互作用[1];例如,电影演员合作网中,节点代表的是演员,而边代表的是演员之间的合作关系[2].

作为复杂网络的一个分支,复杂网络上的传染病动力学吸引了越来越多的关注[3-4].当疾病传播时,人们会通过各种途径获取与疾病相关的信息,进而采取一定的自我防护措施.研究者将人们对于疾病所做出的行为反应纳入传染病动力学模型中,得到了许多丰富的动力学现象[5-6].随着研究的不断深入,单层网络上的传染病动力学也逐渐向多层网络发展[7-10].近年来,基于双层耦合网络的传染病动力学研究也有了许多进展.2013年,Granell等人[8]应用离散时间马尔可夫链的方法研究双层耦合网络上传染病传播和信息传播之间的相互作用,发现传染病传播的阈值行为关于信息传播概率存在一个临界点.2014年,Granell等人[9]又在原来模型[8]的基础上考虑了大众媒体对意识传播的作用,发现大众媒体对疾病信息的传播会导致上述阈值行为的临界点消失.2017年,Huang等人[10]建立了信息更新早于疾病传播的连续时间模型,并证明了全局稳定性.

上述研究均假设在重叠网络上疾病与信息传播模型中信息更新早于疾病传播.但在现实生活中,对于有些个体而言,个体染病之后才意识到某种疾病的传播,即疾病的传播早于信息的更新.为了研究这种非同步次序所带来的影响,我们考虑重叠网络上疾病与信息传播过程中,疾病传播早于信息更新的另一种非同步传播模型.通过利用离散时间马尔可夫链的方法,得到了离散时间动力学方程,计算了疾病暴发的阈值.进一步应用Huang等人[10]的方法,得到了连续时间的动力学方程,发现这种非同步次序对离散时间模型的疾病暴发阈值以及连续时间模型的稳定性结论均无影响.然而随机模拟结果表明,这种非同步次序在传染率较大时对各状态节点,特别是对易感者节点的数量影响较大.随着感染率的增大,相比于疾病传播早于信息更新的非同步次序，在信息更新早于疾病传播的非同步次序下无意识的易感节点的比例更低，而有意识的易感节点比例更高,这说明“先意识后疾病”的非同步更新次序有助于抑制疾病的传播.

1 模型的建立

首先建立一个双层重叠网络(图1:虚线连接的是相同的个体,而实线的连接表示两者之间可以传播疾病或信息),网络的顶层是信息层,即有关于疾病信息传播的网络;而网络的底层是疾病层,即疾病传播的网络.在每一层中节点之间都有不同的连接,但所对应的是同一个个体.在疾病层,个体通过与染病个体接触而传播疾病;在信息层,个体可以通过信息传播而获取关于疾病的信息.在信息层中建立UAU模型,U表示无意识,A表示有意识.在信息传播过程中,个体可以通过与有意识的个体交流以概率λ而获得意识,或者该个体染病之后立即获得意识;另一方面,有意识的个体以概率δ遗忘信息,再次成为无意识的个体.类似的,在疾病层中建立SIS模型,其中S表示易感者,I表示染病者.一个无(有)意识的易感个体被每个染病邻居传染的概率为βU(βA),且βA=γβU.当γ=0时,βA=0,这表明个体获得意识后,不会再次被感染;当γ=1时,βA=βU,这表明意识对疾病无影响.此外,染病个体以概率μ恢复再次成为易感者.

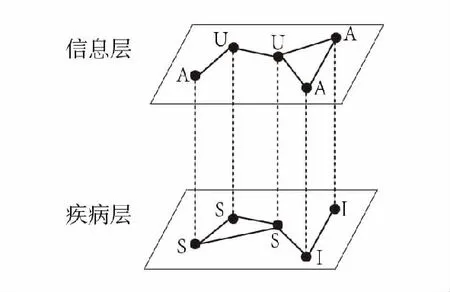
图1 双层重叠网络结构示意图 Fig.1 The illustrative diagram of multiplex network structure

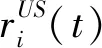
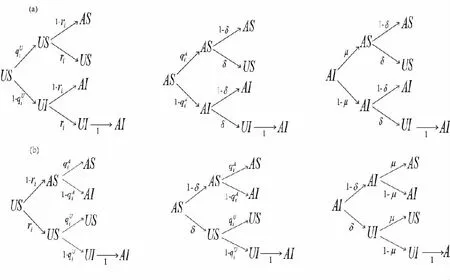
图2 非同步次序下US、AS和AI三种状态的转移概率树

(1)

2 传播阈值

系统(1)的稳态解满足关系式

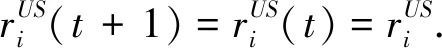
将其代入系统(1)可得

根据已知条件

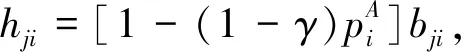
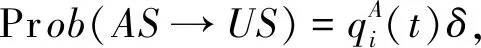
在两种不同步更新次序下得到的转移概率Prob(AS→US)相同.类似地,其他转移概率亦相同,因此,最终所得阈值一样.

3 连续时间模型

应用Huang等人[10]的方法,可将系统(1)中离散的模型改写为:

(2)

为得到疾病传播早于信息更新的连续时间动力学方程,首先将时间间隔从[t,t+1)缩减到[t,t+h),然后令h趋于0.在h个单位时间步长内,状态转移率由λ、δ、βU、βA和μ变为λh、δh、βUh、βAh和μh,则系统(2)就变成

(3)

在疾病传播早于信息更新的次序下,有

(4)

当h充分小时,系统(3)中部分项的值可表示如下:

(5)

类似地,有:

(6)

(7)

(8)

(9)

(10)

进一步,将(5)-(10)代入系统(3)中,并令h→0,则得到如下连续时间动力学方程:

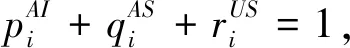
发现所求得的连续时间模型与Huang等人[10]所研究的连续时间模型一致,因此采用该文中的方法,易得同样的稳定性结论.这说明非同步次序对连续时间模型的稳定性无影响.在求连续时间模型的过程中,(5)-(10)的计算结果与Huang等人[10]所得结果一致,原因是在计算过程中忽略掉高阶项o(h2)导致的结果.

4 随机模拟

通过随机模拟来考察重叠网络上疾病与意识传播过程中非同步次序所带来的影响.构建重叠网络,其中网络节点数为N=104,染病个体的恢复率μ=0.2,个体获得意识的概率λ=0.3,个体失去意识的概率δ=0.4,且γ=0.2.

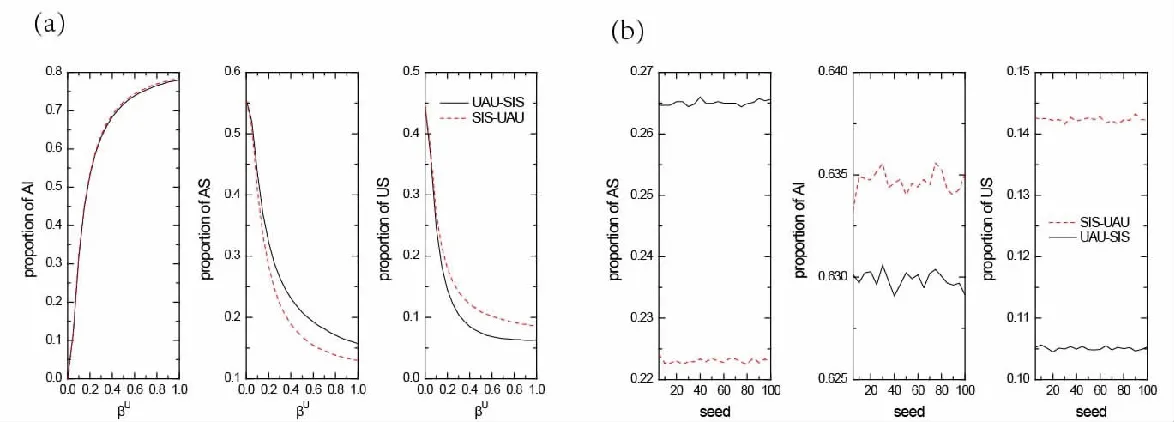
图3 非同步次序下AI,AS,US的密度

图3(a)、(b)分别表示个体在重叠网络上疾病与意识传播过程中非同步次序下AI、AS和US随βU与染病种子(当βU=0.3时)的密度曲线.在图3(a)中初始染病种子数为10.其中,虚线表示重叠网络上疾病与信息传播模型中,疾病的传播早于信息的更新;实线表示重叠网络上疾病与信息传播模型中信息更新早于疾病的传播.在图3(a)中可以发现这种非同步次序在传染率较大时对各状态节点,特别是对易感者(包括有意识和无意识的易感者)的密度影响较大.当βU>0.2时,两种非同步次序下易感节点密度的变化较大,且相比“先信息后疾病”的非同步次序,在“先疾病后信息”的非同步次序下无意识的易感节点的数量较多,而有意识的易感节点的数量较少,这就导致最终染病密度略高.该结果表明信息更新早于疾病传播的非同步次序更有利于控制疾病的传播.在图3(b)中可以发现非同步次序下,染病种子对各状态节点的密度无明显影响.

5 结 论

传染病只能在真实接触网络中通过接触传播,然而线上交流可以传递有关传染病的信息,使个体意识到风险并自我保护式地改变接触行为进而影响传染病的传播.建立重叠网络上疾病与意识传播过程中,疾病传播早于信息更新的SIS-UAU模型.应用马尔可夫链的方法,求得了离散时间模型的疾病暴发阈值,发现非同步次序对该阈值没有影响.在此基础之上,求得连续时间模型的动力学方程,发现得到的动力学方程与信息更新早于疾病传播次序下所得动力学方程是一致的,即非同步次序对连续时间模型的稳定性无影响.之所以无影响,是在计算阈值以及将时间连续化的过程中,忽略掉高阶项所导致的结果.随机模拟结果表明,非同步更新次序在传染率较大时对各状态节点,特别是对易感者(包括有意识和无意识的易感者)数量影响较大,这会对传染过程有一定的影响,但染病种子的比例对各状态节点的密度影响不大.