Gardner同步算法在高速GMSK信号传输中的应用
顾圣明,陈丽婷,陈建斌
(上海航天电子技术研究所,上海 201109)
0 引言
高斯最小频移键控(GMSK)调制属于连续相位调制[1-2],具有很好的频谱性能和恒包络特性。这2种特性使得GMSK调制在遥控遥测领域的应用也日益广泛。目前,中国大多数的脉冲编码调制-调频(PCM-FM)体制遥测系统的码率都不超过2 Mbps[3],少数靶场开始配备10 Mbps码率的GMSK体制遥测系统。但面对越来越高的遥测传输需求,提高GMSK体制遥测系统的传输速率迫在眉睫。通常,限制遥测系统码速率的有硬件平台性能以及位同步所需的过采样率,文献[4]针对GMSK系统提出了一种简单的位同步开环算法,结构简单,但其需要16倍乃至更高的过采样率,且同步性能一般。文献[5]中提出了一种快速捕获的位同步器,主要通过超前滞后信息来完成时钟的“添扣”,达到同步目的,但其精度取决于环路分频即过采样率,同样限制了传输速率。文献[6]提出了一种针对脉冲成型波形的位同步方法,在接收端进行匹配滤波来提取位同步时钟,复杂度低,但只适用于高倍采样系统中。可以看出,目前大多数遥测系统仍通过资源换性能的方法,以高倍采样率来完成高精度的位同步。本文利用Gardner算法,以低倍采样率来完成位同步,在保证相同误码率的条件下提升GMSK信号传输的速率。Gardner算法是利用内插法来实现位同步的方法,通过定时环路调整内插滤波器的位置参数来找到最佳的内插位置,从而恢复位同步信号,主要优点在于不需要调整本地时钟,直接数字处理便可获得同步时钟以及最佳采样点判决信息。本文将Gardner算法应用于GMSK体制中,给出其改进结构和程序设计,并进行仿真和实际测试,最终给出其在GMSK体制中20 Mbps码率下的测试结果。
1 Gardner算法的原理与改进
1.1 Gardner算法的基本原理
如文献[7-9]中所述,Gardner算法的实现流程如图1所示,主要由4部分组成:内插滤波器、环路滤波器、控制器和定时误差检测器,在不改变本地时钟的同时能够实现位同步。同步过程如下:接收端以本地时钟Ts对接收信号重新采样,送入内插滤波器进行内插值的计算,计算出的结果送入定时误差检测器进行误差检测,并送入环路滤波器滤除带外噪声,环路滤波器的输出送入NCO控制器计算内插基点和分数间隔,进行下次内插位置的调整,如此循环往复,从而在最佳采样时刻内插出准确的判决值,即满足位同步条件时的采样值。
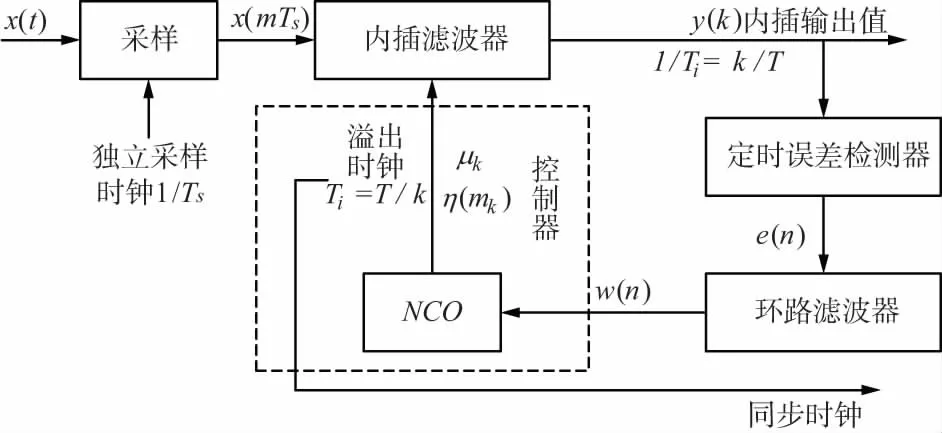
图1 Gardner算法的实现流程
1.2 Gardner算法的改进与设计
1.2.1 内插滤波器设计
内插滤波器[10]是Gardner算法的核心。内插滤波器的作用可以理解为重构后重采样,也就是从离散信号理想地重构出连续信号y(t),再用另一个不同速率或不同初始时刻重新采样。
从采样x(mTs)恢复原连续信号
(1)
再对其进行重采样,可以得到
(2)
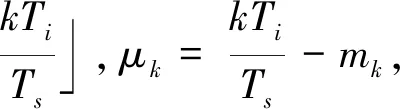
(3)
(4)
式中,μk为计算出的分数间隔,决定内插滤波器的系数大小;mk为插值位置的基点,决定由哪几个位置的采样点计算出内插值;kTi和μk的信息由内部控制器给出。输入与输出的采样时刻关系如图2所示。
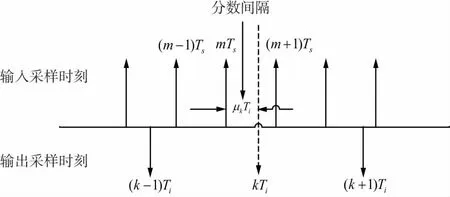
图2 输入与输出的采样时刻关系
从式(4)可以看出,插值输出就是采样点的线性加权和。而且实际上不需要对连续信号完全重构,可以直接从非同步采样到同步采样值。式(4)是无穷项的加权求和,实际上做不到没有误差的理想插值,只能用有限阶的滤波器来实现,即
(5)
式中,μk可以取到0-1之间的所有值,对不同的μk实时计算sinc函数在硬件上难以实现,因此用多项式对理想加权系数进行逼近,即
(6)
显然,阶数取得越大,逼近效果越好。考虑到资源和平衡,本设计采用分段抛物线式滤波器[11],根据文献[12],α=0.5时滤波器具有较好的性能,即
(7)
式中,
(8)
1.2.2 定时误差检测器设计
定时误差检测算法对位同步整体性能起决定性作用。本设计采用GA-TED[13]算法,该算法独立于信号速率,提取出的定时误差可以表示为:
(9)
式中,相邻码元差值表示误差正负即方向,码元中间采样时刻的值代表误差大小。本设计中,用y(n)和y(n-1)的符号代替实际值,来表示误差的方向,即
(10)
采用式(10)可以消除大部分噪声的影响,并且可以避免乘法运算,有利于数字系统的实现。
1.2.3 环路滤波器设计
本文对Gardner算法中的环路滤波器进行了修改,采用二阶环路滤波器[14],具有比较好的跟踪性能。滤波器采用文献[15]中所述的结构,如图3所示。
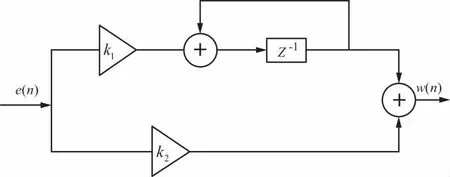
图3 环路滤波器结构
其在Z域上的传递函数为:
(11)
式中,k1=2ξωn/(K*Rs);k2=(ωn)2/(K*R2s);一般来说,阻尼系数ξ取0.707;ωn为环路的自然角频率;ωn=4ξBL/(4ξ2+1);BL为环路带宽,对环路同步速度和精度都有影响。环路增益K=KdKo;Kd为鉴相器增益;Ko为NCO的增益。对上式进行反变换,就可以得到环路滤波器的时域方程:
y(n)=y(n-1)+k1[x(n)-x(n-1)]+k2x(n) 。
(12)
另外,本设计中开放滤波器参数k1,k2接口,如果码元速率变化,NCO参数可以随之变化,实现跟踪。
1.2.4 NCO控制器
Gardner环的控制器主要由NCO以及分数间隔计数器组成。NCO起到一个累减器的功能,0~1累减并给出溢出信号,即确定内插基点位置mk。分数间隔计数器计算出分数间隔μk,作为内插基点后所需要的更精确的位置信息,从而找到最佳采样值。下面给出累减器的差分公式:
ηmk=[ηmk-1-w(mk-1)]mod(1) ,
(13)
式中,ηmk为第mk个时钟时寄存器的值;w(mk)为第mk个时钟时的控制字(环路滤波器输出;,mk为内插基点;k为内插点的序号;NCO的初值设为1。随着采样时钟进行递减,到零时得到内插时钟,确定内插基点,然后开始计算它的分数间隔μk。当环路稳定时,w(mk)就是一个固定值,每隔1/w(mk)个周期就会产生一次溢出,而控制器的工作频率为1/Ts,内插的工作频率为1/Ti,则稳定后w(mk)=Ts/Ti。w(mk)与环路滤波器的具体关系为
w(mk+1)=w(mk)+e(mk) ,
(14)
式中,e(mk)即为环路滤波器的输出。求得w(mk)就可以求得η(mk+1),如果η(mk+1)得负值,则说明NCO寄存器溢出,此时的mk即为内插基点,此时计算出相应的分数间隔μk,并让插值滤波器进行一次内插操作。μk的计算关系如图4所示。

图4 内插间隔的计算示意图
根据图4三角形的相似关系可得:
(15)
(16)
以上就得到了信号的内插基点和分数间隔。
2 程序设计与仿真
本设计是将Gardner算法应用于GMSK体制信号传输中,即对GMSK解调后的基带码元做位同步设计。GMSK体制的解调模块采用文献[16]的设计,即GMSK调制信号经过维特比解调后输出基带码元。经调查,文献[16]采用的是利用超前滞后信息来添扣时钟的位同步方法,需要16倍的过采样率来保证提取精度,如果要实现20 Mbps码速率的传输,其硬件平台需提供320 MHz的采样时钟,对硬件性能要求比较高,因此限制了其码元速率为10 Mbps。
本设计旨在利用Gardner同步算法降低过采样率需求,从而提升传输码速率。在文献[16]中,GMSK解调后的输出码元为不均匀采样的01码元,以4倍采样率为例,输出的码元大部分为4个采样点的码元,少部分为3个或5个采样点的码元,即存在采样偏移,而Gardner算法则是要从这样的码元中找到最佳采样时刻的判决信息。Gardner算法作用示意图如图5所示。
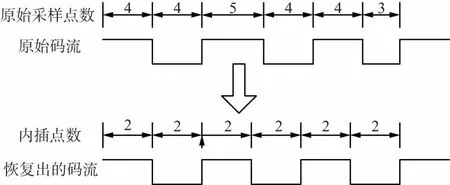
图5 Gardner算法作用示意图
2.1 Matlab仿真
在Matlab中模拟出GMSK解调模块输出的码元并用Gardner算法对其进行位同步,仿真结果如图6所示。可以看出,当存在3个或5个采样点的时候,分数间隔会进行对应调整,偏移内插基点,最终找到最佳采样时刻的判决信息。图中仿真了1 500个码元,分数间隔输出为3 000个点,定时误差和环路滤波输出为1 500个点,正对应于每个码元内插出2个采样点,并输出一个定时误差间隔。经过长时间测试,Gardner位同步模块的误码率为0,性能可靠。
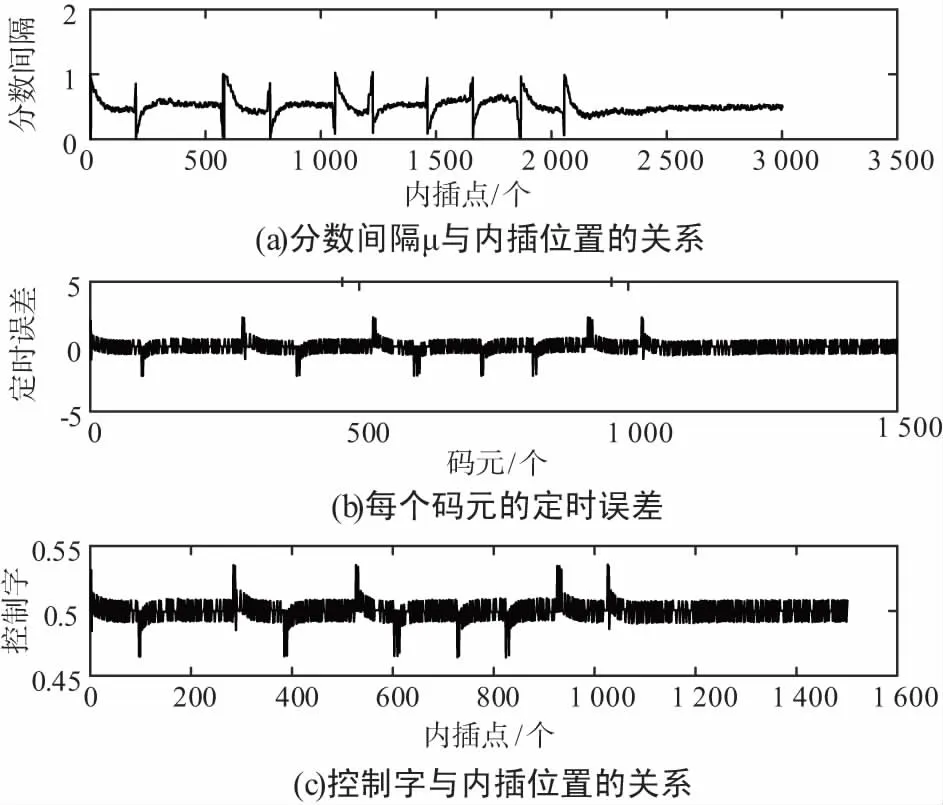
图6 Gardner算法的Matlab仿真图
2.2 FPGA设计
根据1.2节的设计原理,对Gardner算法进行Verilog设计,FPGA采用Xilinx公司K7系列的XC7K160T芯片。GMSK解调模块和Gardner位同步器FPGA设计的顶层图如图7和图8所示,GMSK解调出的基带码元信号送到Gardner位同步模块进行同步。

图7 GMSK解调模块顶层设计
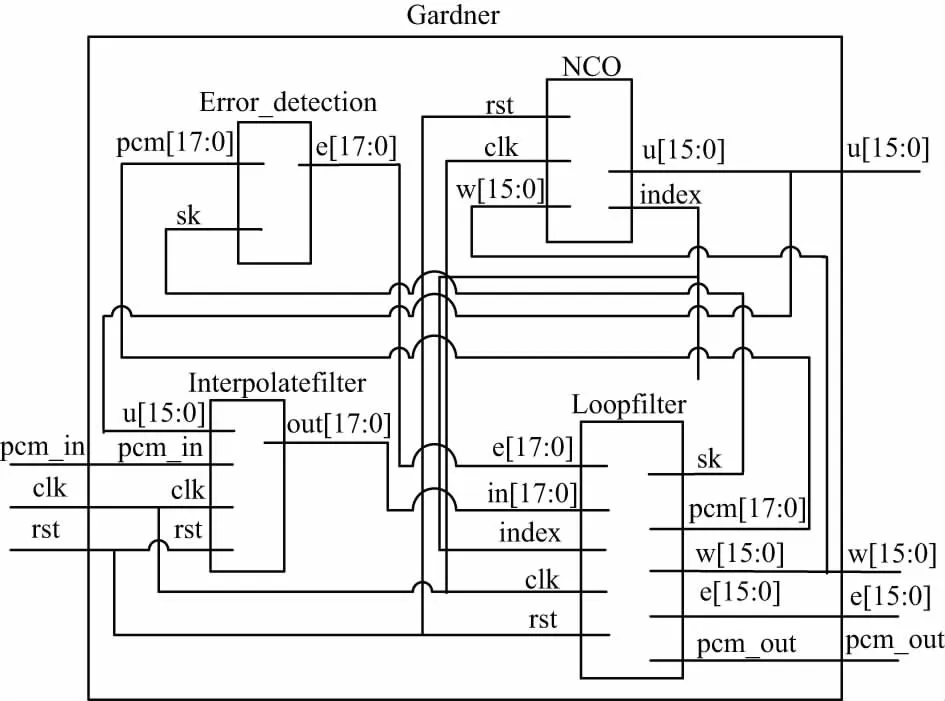
图8 Gardner位同步模块顶层设计
可以看到,Gardner模块分为内插滤波器、控制器、定时误差检测器以及环路滤波器4个模块,最终输出判决码元信息,其中,内插滤波器使用分段抛物线式滤波器,占用了9个加法器和3个乘法器,占用资源很少。另外,程序中除以2的运算都采用移位实现,避免使用除法器,所有变量的寄存器经过计算后均采用最小位数,有效减少了Logic Elements资源的占用。
2.3 FPGA仿真
仿真在Xilinx ISE环境下进行,基带信号由Matlab的Binary generator产生,将码速率设置为10~20 Mbps,NCO及环路滤波器做相应设置,不同码速率仿真出的波形基本相同,仅存在采样速率上的差别,恰巧说明了Gardner算法对不同速率的基带信号均能很好地提取位同步信号。仿真结果如图9所示。可以看到,与第3章中Matlab仿真结果一致,Gardner算法在存在采样偏移的码元处进行内插位置的调整,从而找到最佳采样时刻。
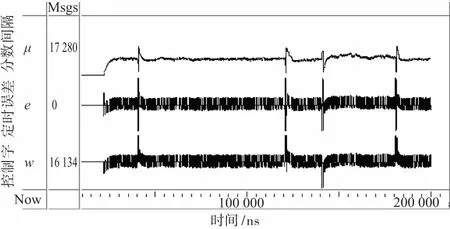
图9 Gardner算法Modelsim仿真结果
根据设计要求,同时对Gardner算法的同步范围进行了测试,同步范围测试即对存在采样率偏移的基带信号,用相同的时钟,滤波器参数等对其进行同步,测试其采样偏移的允许范围。
当10 Mbps码速率40 MHz时钟均匀采样的基带信号由39.8 MHz时钟重新采样后,Gardner算法对其位同步所得到的仿真图如图10所示。可以发现,误差间隔μ按一定周期规律进行调整,原因则在于此时的基带码元存在周期性的采样偏移,由此可知,Gardner算法仍然能有效工作。经测试,Gardner算法能够允许的采样偏移为±1.5%(以此40 MHz数据为例,同步范围为39.4~40.6 MHz),在此范围内,Gardner算法均能准确无误码地提取位同步信号。
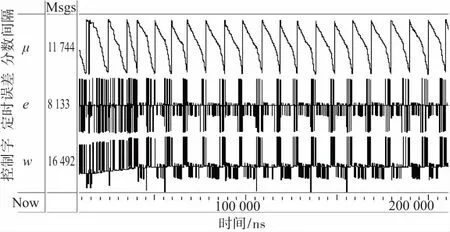
图10 存在采样偏移时Gardner算法的Modelsim仿真结果
3 硬件平台实际测试与分析
本设计中用于实际测试的遥测系统为以AD9361+FPGA为基础构成的软件无线电平台[17-18],如图11所示。GMSK调制信号由RS公司的SMW200A射频信号源给出,AD9361将射频信号搬移到零频送给FPGA进行GMSK解调以及本设计中的Gardner位同步,同步后的码元送入实时软件进行码元对比,测试误码率。

图11 AD9361+FPGA的软件无线电平台
信号源输出的信号为20 Mbps 码速率100 MHz采样率的 GMSK 信号,其中频载波为390 MHz,码元序列采用的是 EB90测试序列。Gardner 码同步器的环路滤波器的参数分别为1.3×10-3和8.9×10-7。
测试过程中,用Chipscope在线逻辑分析仪对Gardner模块中的信号进行抓取,验证其是否正常工作。
Chipscope所抓取出的分数误差间隔μ的工作情况如图12所示。与之前的仿真结果一致,分数间隔μ在出现采样偏移的时刻会进行内插位置的调整,以获得最佳采样时刻,在没有采样偏移的时刻,μ稳定在0.5附近进行均匀内插。
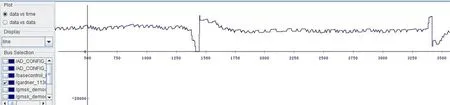
图12 硬件测试时Gardner算法工作情况
Gardner位同步的输出如图13所示。其中,sdin信号即为判决出的码元序列,temp1为其16进制表示,cmpeb90为检测到EB90帧头所输出的同步信号,经过对比,可以发现其波形与信号源中设置的 EB90的Datasource完全相同,Gardner位同步模块正确找到了所有码元的判决信息。

图13 硬件测试时Gardner同步模块的输出
最后,对此GMSK体制信号传输系统进行误码率测试,在低信噪比环境下验证其传输性能,测试结果如图14所示。可以发现,与维特比的理论解调值仅有0.5 dB的损失,此结果也与文献[16]中的误码率一致,说明在码速率提升至20 Mbps的情况下,采用了Gardner位同步算法的GMSK体制在相同误码率的情况下没有造成信噪比的损失,Gardner算法准确找到了所有码元的判决信息。
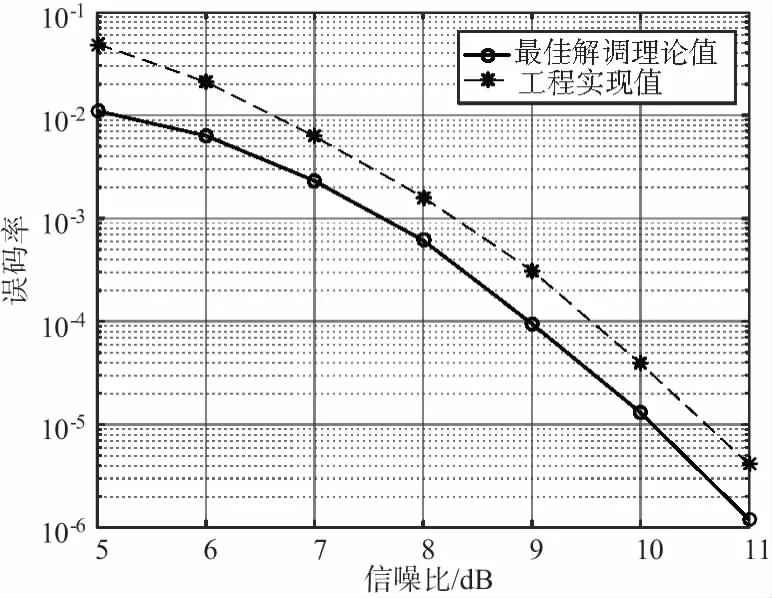
图14 GMSK误码率测试曲线
4 结束语
本文主要研究并实现了Gardner同步算法在GMSK体制高速通信处理中的应用。研究和实验表明,在原有GMSK体制的解调平台下(通信速率10 Mbps),通过采用Gardner位同步算法,降低了同步采样率,将系统的通信速率升级到20 Mbps,提升了系统的性能指标,降低了软件设计的复杂度。另外,Gardner算法所表现出的优异性能并不受调制体制限制,可以将其应用在其他数字解调技术的位同步中,有利于数字接收机的简化以及传输速率的提升。

