一种基于旋转角反射器的双基地前视SAR干扰方法

张 刚，李 涛

(中国人民解放军92728部队，上海 200436)

0 引言

合成孔径雷达(Synthetic Aperture Radar，SAR)是一种主动微波成像传感器，具有全天时、全天候、高分辨二维成像等优点，在海洋观测、军事侦察等领域得到了广泛的应用[1]。近年来，随着收发分离的双基地前视SAR技术研究的深入，突破了传统单基地SAR无法前视的固有瓶颈，增加了侦察系统的隐蔽性和灵活性，也为“察打一体”的作战系统构建提供了有力的技术支撑[2-4]。

双基地前视SAR应用模式灵活多样，导弹与侦察机配合、导弹与导弹配合等，极大扩展了侦察范围，提高了成像雷达的战场感知能力，对重要区域的信息安全构成极大威胁，因此对这种新型侦察手段的干扰方法研究具有重要的现实意义。目前国内外对于单基地SAR的干扰技术研究已较为成熟[5-7]，而对双基地SAR干扰研究的相关文献较少。现有研究中，对双基地SAR的干扰方法主要采用压制式干扰、欺骗式干扰[8]，干扰效果依赖于运动参数的准确获取，实现较难。向伟、刘舫等[9-10]在可散焦容忍准则下，确定了可有效干扰的接收机范围，降低了对接收机定位精度的要求。相对于有源干扰，无源干扰作为传统的干扰方法，不需要知道目标和平台精确的运动信息[11]，且布置、使用方便。其中雷达角反射器旋转时会产生多普勒效应，可干扰SAR/ISAR的成像[12]。孙光才[13]提出了一种基于旋转角反射器的无源压制SAR干扰方法，周阳[14]探讨了该方法对多通道GMTI的对抗性能，但研究均基于单基地SAR进行，未涉及构型复杂的双基地SAR。本文将旋转角反射器引入双基地前视SAR的干扰研究中，建立了旋转角反射器的回波信号模型，推导其成像结果，分析了不同参数下旋转角反射器的干扰特性，并在此基础上提出了可有效干扰不同构型双基地前视SAR的旋转角反射器布阵方式。

1 旋转角反射器的回波信号模型

图1为旋转角反射器的双基地前视SAR成像几何，设发射机坐标为(xT，yT，hT)，接收机坐标为(0，0，hR)，发射机与接收机分别以速度vT、vR沿各自轨道飞行，地面散射点P0坐标为(0，y0，0)，存在一旋转角反射器P以P0为中心做匀速旋转，转动半径为r0，转速为ωs，初始相位为θ0。

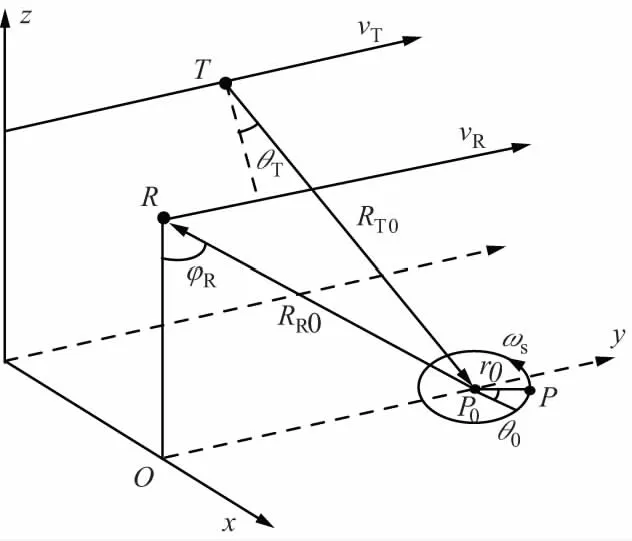
图1 旋转角反射器的双基地前视SAR成像几何

由双基地前视SAR的几何构型得t时刻P0的斜距历程为：

(1)

式中，RT(t)、RR(t)分别为t时刻发射机与接收机到P0的斜距。

则t时刻发射机到旋转角反射器的斜距表达式为：

(2)

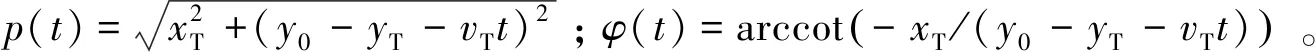
RTP(t)=RT(t)+rTcos(ωst+ψT)。

(3)

同样可得t时刻接收机到旋转角反射器的斜距表达式为：

RRP(t)=RR(t)+rRcos(ωst+ψR)。

(4)

于是到旋转角反射器P的斜距历程为：

(RP(t)=RT(t)+RR(t)+rTcos(ωst+ψT)+rRcos(ωst+ψR)=

k0+k1t+k2t2+k3t3+k4t4+rTcos(ωst+ψT)+

rRcos(ωst+ψR)，)

(5)

式中，k0、k1、k2、k3、k4为R(t)的泰勒展开系数。可以看出，旋转角反射器相当于在斜距历程引入了余弦调制，必然会影响回波信号的距离徙动及方位向脉冲压缩结果。

将旋转角反射器的RCS设为1，则接收机收到旋转角发射器的回波信号经调制解调后，表达式为：

(6)

式中，wr(·)为距离向窗函数；wa(·)为方位向窗函数；τ为距离时间；Kr为距离向调频率；c为光速；λ为载波波长。

2 旋转角反射器回波的成像处理

旋转角反射器的双基地前视SAR回波信号比普通点目标的回波信号更为复杂，也给成像结果的推导带来了困难。本文以参考点P0的成像处理为基础，分析并推导式(6)经成像处理后的表达形式。

2.1 参考点目标成像

点目标P0回波信号s(τ，t)经距离向傅里叶变换后变为：

(7)

式中，fr为距离向频率；f0为载波频率。

对式(7)做方位向傅里叶变换，有：

(8)

式中，fa为方位向频率。为求解驻定相位点t*，首先将R(t)泰勒展开

R(t)=k0+k1t+k2t2+k3t3+k4t4+…。

(9)

根据运用级数反演的方法[15-17]，求得驻相点为：

(10)

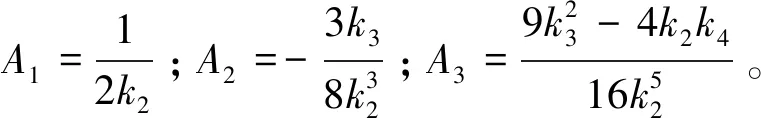
代入式(8)即可得P0点的回波信号二维频谱相位为：

(11)

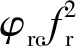
经距离压缩、距离徙动校正、方位压缩后，点目标表达式为：

(12)

式中，R0=k0；B为距离向信号带宽；Bd为方位向信号带宽。

2.2 旋转角反射器成像

在参考点成像处理的基础上考虑旋转角反射器的成像。距离向上，点目标P的回波信号与P0相比，附加了一个随慢时间变化的距离徙动量为：

ΔR=RP(t)-R(t)=rTcos(ωst+ψT)+rRcos(ωst+ψR)。

(13)

因此经双基地SAR的成像处理后，其距离向成像结果为：

(14)

再考虑方位向，与P0相比，方位向多出来的指数项为：

(exp(-jkΔR)=exp(-jkrTcos(ωst+ψT))·

exp(-jkrRcos(ωst+ψR))，)

(15)

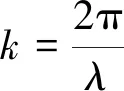
(16)

式中，Jm(·)与Jn(·)为第一类贝塞尔函数。

在不考虑常数相位项时，得：

exp(j(m+n)ωst)。

(17)

(18)

将回波信号在方位向匹配滤波时，匹配滤波器取为exp(-jφaz)，考虑旋转角反射器带来的方位线性项，则方位向匹配滤波为：

(19)

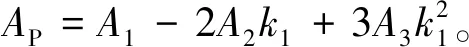
由以上分析得旋转角反射器的回波信号经双基地SAR成像处理后，时域表达式为：

(20)

因此，旋转角反射器的双基地SAR成像结果为距离向位置时变、方位向成对出现的幅度受第一类贝塞尔函数调制的多个像元，即点目标阵。

方位向像元等间隔分布，像元位置为：

相邻像元之间的间隔为：

受转速ws影响，ws越大，间隔越大。由式(20)可见，旋转角反射器回波信号经双基地SAR聚焦后，与单基地SAR形式不同，方位向上受Jm(krT)，Jn(krR)共同调制，因此其有效像元个数也需分开计算。单独使用Jm(krT)调制时，m的有效范围取[-krT-1，krT+1]，单独使用Jn(krR)调制时，n的有效范围取[-krR-1，krR+1]，考虑像元位置t受m+n影响，m+n的有效范围为[-krT-krR-2，krR+krT+2]，因此，方位向有效像元个数为M=2krR+2krT+5。可以看出，方位向有效像元个数受r0影响，r0越大，有效像元越多，但其上限为：

方位像元的时间跨度tL=MΔt，受r0和ws的共同影响，r0越大，ws越大，跨度越大。

第k阶像元的幅度为：

即满足m+n=k的所有调制积之和。

3 旋转角反射器的干扰特点

3.1 图像特征

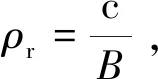
① 直线型。当Δx≤ρr，且Δy≤ρa时，各像元将在距离向上位于同一距离分辨单元，方位向上无法区分，旋转角反射器所成的像为一条沿方位向分布的直线。

② 直线点列型。当Δx≤ρr，且Δy>ρa时，各像元在距离向上位于一个分辨单元内，在方位向上位于不同的分辨单元，所成图像为一串在方位向等间隔分布的直线点列。

③ 直线条带型。当Δx>ρr，且Δy≤ρa时，各像元在距离向上将占据多个距离单元，在方位向上无法区分，此时所成的像为一条沿方位向分布具有一定距离向宽度的条带。

④ 直线圆列型。当Δx>ρr，且Δy>ρa时，各像元在距离向上按余弦规律占据多个距离单元和不同的方位分辨单元，旋转角反射器所成的像为沿方位向等间隔分布的圆列。

3.2 布阵方式

单个旋转角反射器仅能在方位向形成干扰条带，在距离向展宽有限。那么沿距离向放置多个角反射器可对SAR进行区域干扰。但是双基地前视SAR构型特殊，应用灵活，隐蔽性强，无法准确得知接收机的飞行轨迹，而干扰效果依赖于接收机飞行轨迹与角反射器阵的夹角。针对这一问题，本文提出一种三角形旋转角反射器布阵方式，如图2所示，可应对不同构型的双基地前视SAR。

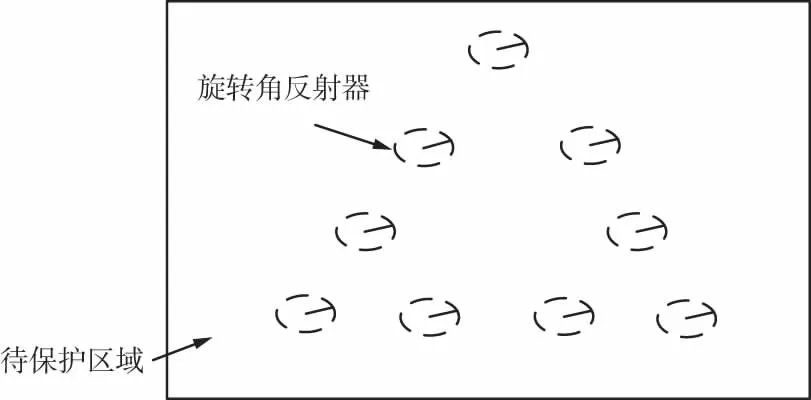
图2 旋转角反射器三角形布阵方式

在实际应用中，需根据侦察到的双基地前视SAR的系统参数，结合预期的干扰效果，合理设置旋转角反射器的数量、位置，选择适当的半径和转速，以达到有效的遮蔽干扰效果。

4 仿真实验

采用仿真实验验证本文分析的有效性，双基地前视SAR系统参数设置如表1所示。

表1 双基地前视SAR系统参数

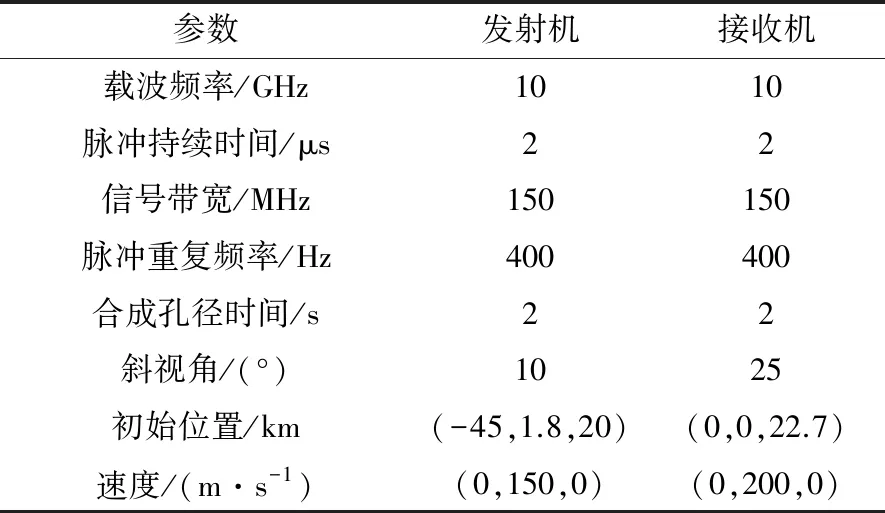
参数发射机接收机载波频率/GHz1010脉冲持续时间/μs22信号带宽/MHz150150脉冲重复频率/Hz400400合成孔径时间/s22斜视角/(°)1025初始位置/km(-45,1.8,20)(0,0,22.7)速度/(m·s-1)(0,150,0)(0,200,0)

单个旋转角反射器位于(0，10.6，0) km处。设置4组参数：

①r0=0.2 m，ωs=π rad/s；

②r0=0.2 m，ωs=3π rad/s；

③r0=1 m，ωs=π rad/s；

④r0=1 m，ωs=10π rad/s。

仿真结果如图3所示。

图3 旋转角反射器在不同旋转半径和转速下的成像结果

根据系统参数可计算得ρr=2 m，ρa=2 m。使用第①组参数时，仿真结果如图3(a)所示，此时Δx=0.54 m，Δy=1.6 m，点目标在距离向分布于同一单元，方位向的点目标间隔较小，图像特征表现为一条直线段，像素的明暗变化是贝塞尔函数对幅度调制的结果。使用第②组参数时，仿真结果如图3(b)所示，Δy=4.8 m，大于ρa，此时方位向点目标可在图像上区分开来，表现为一条直线点列。使用第③组参数时，仿真结果如图3(c)所示，此时Δx=2.68 m，Δy=1.6 m，像元在存在一定的距离徙动，点阵在距离方向展宽，角反射器的回波信号在图像上表现为一条直线型的条带。使用第④组参数时，仿真结果如图3(d)所示，此时点阵在距离向上展宽，方位向上像元间隔增大，表现为直线圆列型。

对比图3(a)和图3(b)，转速ωs的增大可增加干扰点之间的距离，带来方位向的展宽，形成一定的欺骗干扰效果，但是转速过大时，点目标过于分散，将无法形成有效干扰，因此转速选取不宜过大。对比图3(c)和图3(d)可发现，图3(c)方位向点目标较为密集，这是由于r0过大时，同一点目标的回波在距离向位置的徙动过大，接收机的成像处理未对此徙动量进行校正，使得对同一点目标的回波信号沿距离向分散，经聚焦形成多个沿距离向分布的点目标，但其幅度会有所减小，同时也会造成一定程度的方位散焦，使得方位向的点目标间隔比理论值更小。r0过大时方位向散焦严重，会造成干扰效果的减弱，因此在实际应用时，不宜采用半径过大的旋转角反射器。

按图2所示的三角形阵列排列9个旋转角反射器。三角形3个顶点的坐标分别为(3.9×10-3，10.57，0) km、(-2.06×10-2，10.55，0) km、(1.29×10-2，10.54，0) km，相邻旋转角反射器间隔为11.5 m，旋转角反射器参数设置为r0=0.2 m，ωs=1.5π rad/s。第1组参数设置发射机高度为1 500 m，斜视角为20°，其他参数同表1，此时仿真结果如图4(a)所示。第2组参数设置发射机高度为2 500 m，斜视角为30°，其他参数不变，此时仿真结果如图4(b)所示。

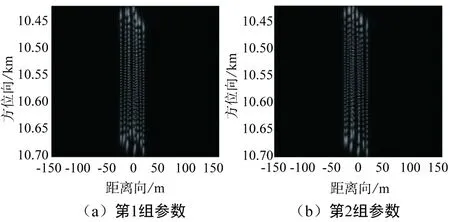
图4 不同参数时三角形旋转角反射器阵列的干扰效果

从图4可以看出，使用三角形旋转角反射器阵列，可在SAR图像中形成大片遮挡，为重点区域提供压制性的保护。当发射机参数改变时，仍可在SAR图像中形成大片遮挡，表明三角形旋转角反射器阵列对不同构型的双基地前视SAR具有都有较好的干扰效果。实际应用中，还可采用不同参数的角反射器组成干扰阵列，增加雷达对目标识别的难度。

5 结束语

本文以旋转角反射器对双基地前视SAR的干扰特性研究为出发点，建立了旋转角反射器在双基地前视SAR系统照射下的回波信号模型，基于级数反演法推导了旋转角反射器的成像结果，研究了不同参数下旋转角反射器的单个旋转角反射器呈现的图像特征。

针对旋转角反射器干扰成像在距离向展宽有限的特点，提出一种三角形布阵方式，可对各种构型的双基地前视SAR均可形成较好的二维遮蔽干扰效果。通过仿真验证了理论推导的正确性和所提干扰方法的有效性，对双基地前视SAR的无源干扰研究具有一定的指导意义。