培养学生思维，践行核心素养——对一道中考压轴题的思考

☉湖北省恩施州清江外国语学校 杨昌龙

核心素养的研究是当今的热潮.研究中考试题对核心素养的评价，对教师在平时的教学中如何落实核心素养，具有很强的现实意义.下面就一道中考压轴题为例，谈谈践行核心素养的一些思考.

一、原题呈现，简约精彩

原题：矩形AOCD绕顶点A（0，5）按逆时针方向旋转，当旋转到如图1所示的位置时，边BE交边CD于点M，且ME=2，CM=4.

（1）求AD的长.

（2）求阴影部分的面积和直线AM的解析式.

（3）求经过A、B、D三点的抛物线的解析式.

图1

本题文字言简意赅，图形直观、明了，从知识上看，考查四边形、旋转变换、勾股定理、方程模型等知识，融合了矩形、直角三角形及相似形、一元二次方程等有关知识；从核心素养方面看，考查学生直观想象、数学抽象、数学建模、逻辑推理、数学运算等核心素养.下面从题目条件、图形、设问等几个方面进行分析.

1.条件设计精妙

题目条件寥寥数字，结合图形，清晰明白.条件1：矩形AOCD在坐标系中，且两边在两坐标轴上.条件2：点A的坐标为（0，5）.条件3：矩形ABEF是由矩形AOCD绕点A按逆时针方向旋转而得的，且BE交CD于点M.条件4：ME=2，CM=4.

由条件1、2可知CD=OA=5，AD=OC. 由条件3可知AB=OA=5，BE=OC=AD. 由条件4可知ME=2，BM=BEME=AD-2，DM=CD-CM=OA-CM=5-4=1.

通过对题目条件的思考，发现题目条件在巧妙的构思中考查学生对矩形、图形的旋转等知识的掌握情况，更是对数形结合思想的考查，也体现了对直观想象及逻辑推理等核心素养的考查.

2.图形简约、直观

本题中的图形由直角坐标系和两个全等的矩形组成，简约、直观，且阴影部分清晰、明了.学生在分析图形时，易看、易懂，容易接受，体现了对直观想象核心素养的考查.

3.设问环环相扣

本题共四问，逐层深入，环环相扣.第（1）问求AD的长是后三问的基础，因此第（1）问能否顺利解答至关重要.第（2）问求阴影部分的面积和直线AM的解析式，只要第（1）问中求出了AD的长，阴影部分就可分解成两个直角三角形进而求出面积.易知点M的坐标，也就可以求出直线AM的解析式.第（3）问主要是求B点的坐标，只要把B点的坐标求出来，就易求出抛物线的解析式.第（4）问是存在性问题，知道点A、M的坐标寻求P点，利用求三角形面积的方法不难得到方程组，但本问涉及分类思想和较繁的计算，给学生提供了一个较大的思维空间，学生不仅要具备较强的分析能力，而且要有较强的运算能力，因此学生要想得到满分很困难.每一问相互联系，逐次递进，从不同角度考查了学生的数学建模、逻辑推理、数学运算等核心素养.

二、解法多样，尽展风采

1.构建模型，层层递进

本题第（1）问紧紧围绕矩形的特征、旋转的不变性，寻求等量关系，构建方程模型.本问对学生来说，有一定的难度，不易直接找到思考方法，特别是作辅助线利用相似三角形和勾股定理构建方程模型，或者直接利用勾股定理构建方程模型，是本问的难点.这一问不能突破，将直接影响后继的解题，所以本问是关键.

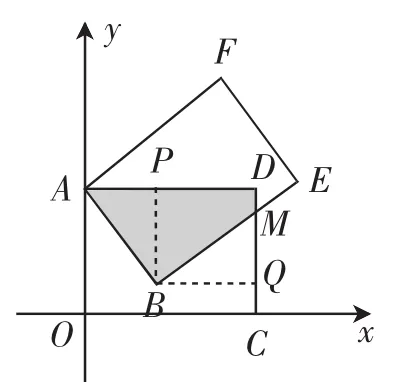
图2

解法2：连接AM，设AD=x，由矩形的性质和旋转的性质，可知AB=5，BM=x-2，DM=5-4=1.

在Rt△ABM与Rt△ADM中，52+（x-2）2=AM2=x2+12，进而可求得AD的长.

以上两种解法，均是由勾股定理构建方程模型，解法1是由相似三角形及完全平方公式的变形获得关系式，两者的结合是本问的难点；解法2借助两个直角三角形公共的斜边构建方程.学生只要充分思考已知条件，想到方程，这样层层递进，逐级思考，就能最终获得求解.

对于第（2）问，易得△ABP和△MBQ全等，通过勾股定理构建方程，求得MQ的长，于是可得BQ的长，阴影部分的面积就易得了，然后利用待定系数法求直线AM的解析式.也可直接求Rt△ABM与Rt△ADM的面积和.

对于第（3）问，只要确定B点的坐标，即可利用待定系数法求得抛物线的解析式.因此，求B点的坐标尤为关键.若第（1）问用三角形相似求解，则B点的坐标易知.若按解法2，则需要作辅助线求点B的坐标.

2.挖掘内涵，演绎分类

第（4）问属存在性问题，是中考压轴题常考的问题，全方位考查学生的能力，对学生要求较高.特别是分类思想，学生最易出现问题.因此，充分挖掘题目的内涵，找准关键所在，寻求恰当的方法，才能使问题得以解决.

方法1：设P点在线段AM下方的抛物线上时，过P点作纵轴的平行线，利用三角形面积为水平宽度与铅直高度乘积的一半构建方程，从而求得点P的坐标.由P点的坐标，易求过点P且平行于AM的直线的解析式，从而得到P点到直线AM的竖直高度.通过平移，可得过线段AM上方抛物线上P点的直线的解析式，联立抛物线和直线的解析式，进而求得P点的坐标.

方法2：求出了抛物线的解析式，掌握了求三角形面积的方法，自然可以得到各种情况，不需首先考虑分类.三角形面积是水平宽度与铅直高度的积的一半.在抛物线上两定点的水平距离称为水平宽度，过动点作抛物线的对称轴的平行线，与经过两定点的直线相交，其交点和动点之间的线段的长度称为铅直高度.这样第（4）问中，水平宽度为AD的长7，铅直高度为动点P的纵坐标与交点的纵坐标差的绝对值，进而转化成两个一元二次方程，求出方程的解，即可得到动点P的坐标.

当然第（4）问在解一元二次方程时，计算较复杂，要求学生不仅有熟练的计算能力，而且要能灵活变形.

三、探究数学思想，贯彻核心素养

数学思想方法是解决数学问题的核心.中考压轴题是渗透数学思想方法一个很好的平台.本题从多个角度让数学思想方法得到了充分体现，贯彻了数学学科核心素养的培养.

1.建模思想

新课程标准给出了数学学科核心素养的六个方面，其中一个就是数学建模.本题在第（1）问就是利用勾股定理构建方程模型，如解法（2）中利用Rt△ABM与Rt△ADM两个直角三角形有公共的斜边AM，作为等量关系，构建方程，从而求得AD的长.当然，本题中的模型构建有一定的难度，辅助线不易想到，入口较窄，致使学生思维受困.

2.数形结合思想

在压轴题中，数形结合思想非常普遍，几乎每道题都有涉及，通过坐标系建立起点与数的对应关系，既可应用代数方法研究几何图形的性质，又可借助几何直观，得到某些代数问题的解答.本题中数形结合较多，第（1）问求AD的长就利用点A的坐标得到了AB的长，进而获得解答.第（3）问求抛物线的解析式，也是通过求点B的坐标，由待定系数法求得解析式.第（4）问更是体现得淋漓尽致，方法1就是通过图形得到P点的几种情况，把直线平移，得到其解析式，从而求得点P的坐标.无论是由坐标得线段长度，还是由图形得到点P的坐标，都是从数到形，或者从形到数的过程，充分体现了数与形的结合.

3.分类讨论思想

分类讨论思想是对学生更高层次的考查，不仅检测学生的知识水平，更检测学生思维的准确性和严密性，常常通过条件的多变性或结论的不确定性来考查.本题的第（4）问就需要进行分类讨论，点P在直线AM的下方，以及P点在直线AM的上方，求出P点的坐标后，还要进一步考查P点的合理性.

通过对本题涉及的思想方法的分析，中考题可以以不同的方式进行考查，但数学思想方法始终在压轴题中得以体现，因此，平时的教学中，应强化对中考题的研究，注重数学思想方法的渗透，有效贯彻核心素养的培养.

四、引申推广，拓展探究

1.改变条件

本题第（1）问还可以把条件改变，如：把边BE交边CD于点M改为直线BE交直线CD于点M，且ME=m，CM=n，这样在求AD的长的过程中，就需要考虑M点的不同位置了，尽管结果一样，但对学生的思维的要求提升了.还可把矩形旋转改为矩形折叠，比如，恩施州2016年中考第24题.

2.改变结论

第（2）问求直线AM的解析式可改为求直线AE、AF、BF、EF等的解析式，主要考查学生对点的坐标及一次函数知识的掌握情况.

第（3）问求抛物线的解析式也可改为过点A、E、D的抛物线，过点A、F、D的抛物线等，主要考查利用待定系数法求二次函数的解析式.第（4）问是存在性问题，可改为求极值问题，比如，在直线AM下方的抛物线上找一点P，使三角形PAM的面积最大.

五、对教学的启示

1.重视方法总结，探究渠道多样

平时的教学中，教师应积极研究中考试题及命题方法，有意识地把相关的知识与方法贯穿于教学中.中考压轴题的教学应注重以下几个方面.（1）数学思想，主要是数形结合思想、分类讨论思想、从特殊到一般的思想.大部分中考压轴题几乎都涉及这几种数学思想方法的考查.本题就注重考查数形结合、分类讨论及数学建模等.（2）探究问题，主要是三角形、平行四边形（包括矩形、菱形、正方形等）、圆等的探究；动点、动线、动图形的探究，比如，本题就是动图形的探究；特殊角（直角、45°角、60°角等）的探究；线段极值、面积极值的探究；图形变换中特殊点活动范围的探究等.（3）解题方法，主要是直观观察法、数形结合法、解析法等.

2.注重学生能力，培养学生核心素养

数学学科核心素养的考查是每一份中考试题都必须关注的.压轴题就是知识点的综合，思想方法的集中，解决办法的多变，思维高度的提升.从背景取材到问题设置，不仅综合性强，而且创新性强，既注重知识的考查，又注重能力方法的考查，多方面考查学生的核心素养，从本题中可见一斑，方程的数学建模、画图后的直观想象、变化图形的数学抽象、每问的逻辑推理及最后一问运算能力的考查等都得以体现.因此，在平时的教学过程中，要重视知识的梳理归纳、计算能力的培养、实际问题中数学问题的抽象、数学思想方法的渗透等，最终达到培养学生数学学科核心素养的目的.W