从一道中考压轴题说开去

☉安徽省六安市舒城第二中学 张 军

纵观全国各地的中考试卷，绝大部分压轴题都与二次函数密切相关.对于二次函数压轴题，只要我们认真审题、把握试题的特点与结构，注意转化思想、数形结合思想、分类讨论思想、方程思想的应用，不断总结解型规律与方法，问题解决自然水到渠成.

原始母题：（2018·自贡）如图1，抛物线y=ax2+bx-3过A（1，0）、B（-3，0）两点，直线AD交抛物线于点D，点D的横坐标为-2，点P（m，n）是线段AD上的动点.

（1）求直线AD及抛物线的解析式；

（2）过点P的直线垂直于x轴，交抛物线于点Q，求线段PQ的长度l与m的关系式，m为何值时，PQ最长？

分析：对于第（1）问，根据待定系数法，可得抛物线的解析式；根据自变量与函数值的对应关系，可得D点的坐标，再根据待定系数法，可得直线的解析式.对于第（2）问，根据平行于y轴的直线上两点间的距离是较大的纵坐标减较小的纵坐标，可得二次函数，根据二次函数的性质，可得答案.

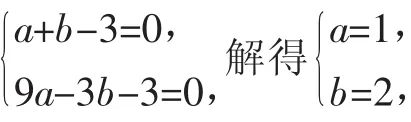
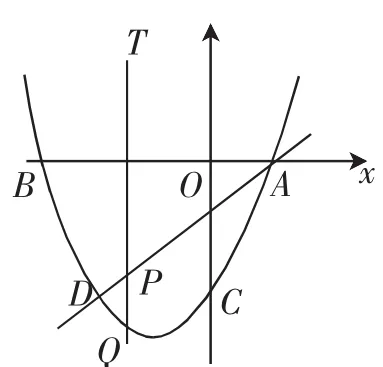
图1

当x=-2时，y=（-2）2+2×（-2）-3y=-3，即点D（-2，-3）.

（2）由于点P在直线y=x-1上，可设P点的坐标为（m，m-1）.

由PQ∥y轴，得点Q的横坐标也为m.又点Q在抛物线y=x2+2x-3上，则点Q的坐标为（m，m2+2m-3）.

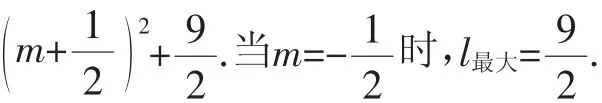
点评：与y轴平行的竖直线段的长等于上点的纵坐标减去下点的纵坐标，同理，与x轴平行的水平线段的长等于右点的横坐标减去左点的横坐标.求两个函数图像上两点距离的最值需要建立二次函数关系式，利用二次函数最值的性质去解答.设点的坐标，然后用表示坐标的代数式表示线段长是解决动点问题常用的方法.

变式方向一：求水平线段的最值

承原始母题第（2）问，如图2，过点Q作QM∥x轴，交直线AD于点M，则线段MQ有最大值还是最小值？请求出这个最值.

分析：我们已经求得线段PQ的最大值，线段PQ与线段QM在同一三角形中，如果能得到这两条线段的关系，就能利用线段PQ的最值求得线段QM的最值.

解析：由直线AD的解析式为y=x-1，得直线AD与直线y=x平行.又直线y=x与x轴的夹角是45°，则直线AD与x轴的夹角也为45°，即∠BAO=45°.又直线PQ∥y轴，即直线PQ垂直于x轴，则∠TPA=45°，则∠MPQ=45°.

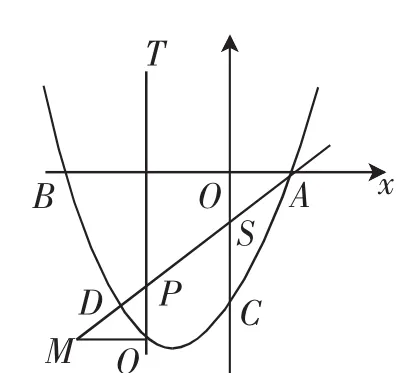
图2

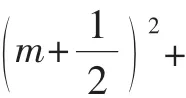
点评：从本题得：欲求水平线段的最值，需要把水平线段转化为竖直线段，通过竖直线段建立二次函数模型，求出竖直线段的最值，从而得到水平线段的最值，这里体现了转化的数学思想.不能认为只有△PQM是特殊直角三角形，才能得到线段PQ与线段QM的关系，其实△PQM只要是直角三角形即可，因为易证△PQM与△OSA相似，而△OSA的三边已确定.

变式方向二：求斜线段的最值

承原始母题第（2）问，如图3，过点Q作QE⊥AD，垂足为点E，则线段QE有最大值还是最小值？请求出这个最值.

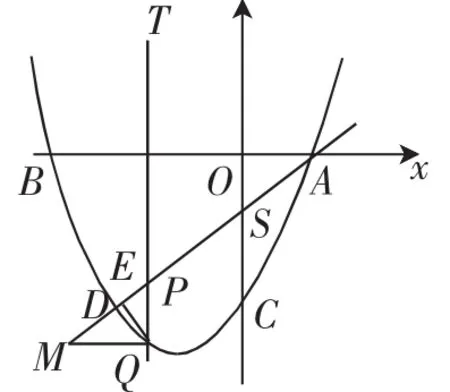
图3

分析：在第（2）问的基础上，已经求得线段PQ的最大值，线段PQ与线段EQ同在△PEQ中，得到线段EQ与PQ的关系，就可以求得斜线段EQ的最值.

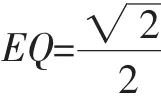
点评：从本题可以看到：欲求斜线段的最值，也需要把斜线段转化为与y轴平行的竖直线段，因为与y轴平行的竖直线段的长与动点的横坐标之间易建立二次函数关系式，利用二次函数最值的性质得竖直线段的最值，从而得到斜线段的最值.这里有一个中间环节，即得到线段EQ与PQ的关系式，上述解法是根据等腰直角三角形的性质得到的，也可以根据△EPQ与△OSA相似，由相似三角形对应边成比例，得到斜线段EQ与竖直线段PQ的关系.

变式方向三：求三角形周长的最值

承原始母题第（2）问，如图3，过点Q作QE⊥AD，垂足为点E，则△PQE的周长有最大值还是最小值？请求出这个最值.

分析：△PQE的周长=EP+EQ+PQ，在第（2）问中，已得线段PQ的最值，如果能将其他两条线段都转化为用PQ表示的式子，就可以将△PQE的周长转化为用线段PQ表示的式子，从而求得△PQE的周长的最值.

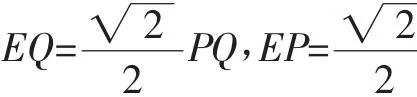
点评：从本题可以看出，欲求三角形周长的最值，也需要将三角形的周长转化为竖直线段的长，其实，解答数学问题的过程就是不断转化的过程，把陌生的问题转化为熟悉的问题，把复杂的问题转化简单的问题，把大问题转化为小问题，从而实现问题的解答.

变式方向四：求三角形面积的最值

承原始母题第（1）问，如图4，在直线AD下方的抛物线上有一点Q，连接QD、AQ，则△ADQ的面积有最大值还是最小值？请求出这个最值.

分析：当点Q在直线AD下方的抛物线上移动时，△ADQ的面积随点Q位置的变化而变化，即随点Q横坐标的变化而变化，所以需要建立△ADQ的面积与点Q横坐标的函数关系式，然后求最值.

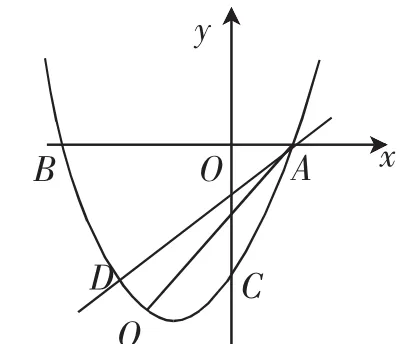
图4

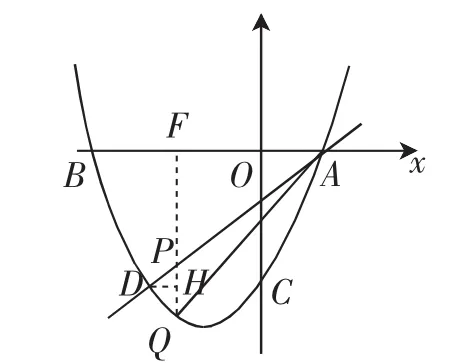
图5

解析：如图5，过点Q作QF⊥x轴，交x轴于点F，交直线AD于点P，过点D作DH⊥FQ于点H，则△ADQ的面积=△DPQ的面积+△APQ的面积=PQ·DH+PQ·AF=PQ·（DH+AF）.由DH+AF就是点A与点D的水平距离，点A（1，0）、D（-2，-3），得DH+AF=1-（-2）=3.则△ADQ的面积=PQ，则当PQ最大时，△ADQ的面积也最大.由原始母题第（2）问，得：设P点的坐标为（m，m-1），点Q的坐标为（m，m2+2m-3），则PQ=（m-1）-（m2+2m-3）=-.则△ADQ的面积

点评：从本题可以看出，欲求三角形面积的最值，同样需要将三角形面积转化为用竖直线段表示的式子，从而利用二次函数最值的性质解答.在坐标系中求三角形的面积，如果三角形的任何一边都不是水平的或竖直的，应将三角形分割与添补，使分割或添补后的三角形至少有一边是水平的或竖直的，这样才可能用点的坐标表示线段的长，从而将图形的面积转化为用点的坐标表达的式子.

在二次函数压轴题的最值问题中，牢记一条线段：竖直线段，一个数学思想：转化思想，四种转化：水平线段转化为竖直线段，斜线段转化为竖直线段，三角形的周长转化为竖直线段，三角形的面积转化为竖直线段.其实，知识就像蘑菇一样，会成堆地生长，只要我们细心观察与思考，很多知识或试题有相通的地方，通过这样的总结与训练，有利于提高学生分析问题与解决问题的能力，更有利于学生创新能力的培养.W