立足学生发展，让学生真正“有话可说”——记初三数学复习课“探索数式规律性问题”

☉浙江省湖州市第五中学凤凰校区 白 艳

规律性问题是近年来中考数学的热点题，这种题型可考查学生观察、比较、探索问题的能力.学生必须具有综合的数学能力和实践能力，才能较好地解答此类问题.在实际教学过程中，学生面对这种题目往往手足无措，无法找到其内在关系.

针对学生的这一问题，笔者开设了一节专题复习课“探索数式规律性问题”，以期在方法上对学生进行一些指导和帮助，并在第一次上课—评课、修改教学设计—第二次上课（不同班级）—课后反思的过程中学到了很多.

一、备课、教学初体验

初中三年的数学学习中，大多数学生对简单的规律性问题的解决能做到得心应手，但遇到偏难的问题时，会束手无策，因此在初次备课时，笔者的侧重点在于较难的规律性问题，具体的教学设计如下：

师：今天我们来研究专题：规律性问题，在中考题中主要有以下几种类型.

【初试数式规律】

呈现例题：

观察下列数的排列规律，并完成填空.

1.1，4，9，16，25，______，49，…，则第100个数是______.

2.0，3，8，15，24，…，则第2002个数是______.

学生回答，教师点评，并提问：在解题时，你认为解题的关键是什么？

解题锦囊：

编序号—找“关系”—验证.

探囊取物：

1.古希腊数学家把数1、3、6、10、15、21、…叫作三角形数，其中1是第1个三角形数，3是第2个三角形数，6是第3个三角形数，…，以此类推，那么第9个三角形数是____，2016是第____个三角形数.

2.观察下列等式：

……

按上述规律，回答以下问题：

（1）用含n的代数式表示第n个等式：an=______；

（2）a1+a2+a3+…+an=______.

3.下面是按一定规律排列的一列数：

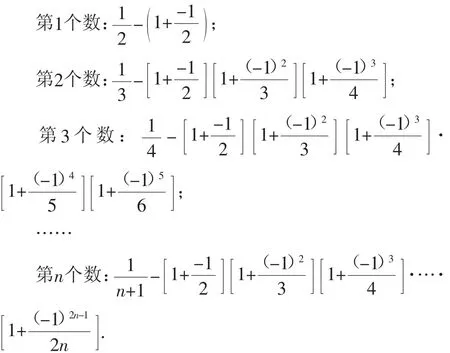
那么，在第10个数、第11个数、第12个数、第13个数中，最大的数是（ ）.

A.第10个数 B.第11个数 C.第12个数 D.第13个数

【再探图形规律】

例题教学：如图1，自左至右，第1个图由1个正六边形、6个正方形和6个等边三角形组成；第2个图由2个正六边形、11个正方形和10个等边三角形组成；第3个图由3个正六边形、16个正方形和14个等边三角形组成……按照此规律，第n个图中正方形和等边三角形的个数之和为______.

图1

解题锦囊：

编序号—找“关系”—验证.

探囊取物：

如图2，图（1）是一个水平摆放的小正方体木块，图（2）、（3）是由这样的小正方体木块叠放而成的，按照这样的规律继续叠放下去，至第7个叠放的图形中，小正方体木块总数应是（ ）.

A.25 B.66 C.91 D.120

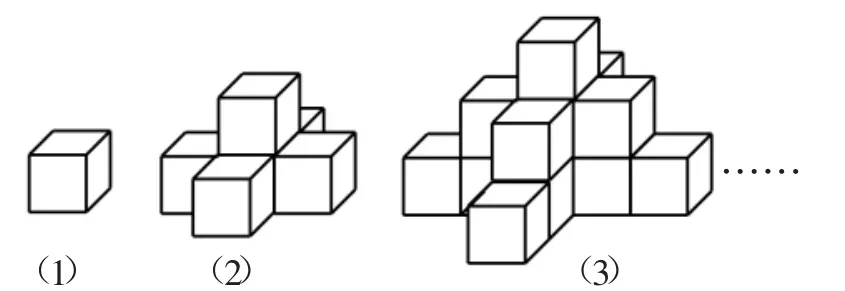
图2

解题锦囊：

编序号—分类（累加、分区、循环）—找“关系”—验证.

【三探坐标系中的规律】

探囊取物：

1.如图3，在平面直角坐标系中，直线l：y=x+2交x轴于点A，交y轴于点A1，点A2、A3、…在直线l上，点B1、B2、B3、…在x轴的正半轴上，若△A1OB1、△A2B1B2、△A3B2B3、…依次均为等腰直角三角形，直角顶点都在x轴上，则第n个等腰直角三角形AnBn-1Bn的顶点Bn的横坐标为＿＿＿＿＿＿.

2.如图4，一段抛物线：y=-x（x-2）（0≤x≤2）记为C1，它与x轴交于两点O、A1；将C1绕点A1旋转180°得到C2，交x轴于点A2；将C2绕点A2旋转180°得到C3，交x轴于点A3……如此进行下去，直至得到C6，若点P（11，m）在第6段抛物线C6上，则m=＿＿＿＿＿＿.

3.如图5，正△ABO的边长为2，O为坐标原点，点A在x轴上，点B在第二象限，△ABO沿x轴作无滑动的翻滚，经一次翻滚后得到△A1B1O，则翻滚3次后点B对应的点的坐标是＿＿＿＿＿，翻滚2017次后AB的中点M经过的路径长为＿＿＿＿＿.

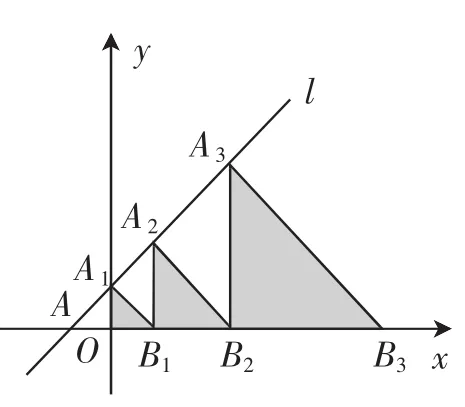
图3

图4

图5

二、评课及修改教学设计

课后，笔者进行了深刻的教学反思，教学师傅也提出了建议和意见：在例题教学中，由于找规律题目可以有多种方法，学生疲于计算和接受，自主思考较少，教师讲评较多，应当减少课堂容量，关注学生思考和互动；在练习环节，题目容量较大，计算量较大，学生无暇思考，课堂氛围死气沉沉，完全没有达到预期目的，教师讲评又太细，应增加师生互动环节，减少题目数量.

三、二次上课，迸发教学“火花”

听取了教学师傅的建议和意见，结合笔者在教学过程中发现的问题，笔者对教学设计进行了一些修改：增加课前练习部分，启发学生积极思考和互动；减少例题数量，同时积极启发学生思考解题方法，主动获取解题技巧.

【小试身手】

找规律，完成下列填空：

1.1，3，5，7，＿＿＿＿＿＿，11，13，…；

2.2，4，6，8，＿＿＿＿＿＿，12，14，…；

3.1，3，6，10，＿＿＿＿＿＿，21，28，…；

4.1，4，9，16，＿＿＿＿＿＿，36，49，…；

5.1，2，4，8，＿＿＿＿＿＿，32，64，…；

6.0，3，8，15，＿＿＿＿＿＿，35，＿＿＿＿＿＿，63，…；

7.2，6，12，20，＿＿＿＿＿＿，42，56，….

学生自主思考，然后分享解题技巧.

先呈现第1～5题，学生立刻找到答案，增强了学生的解题信心.第6～7题相对难度加大，学生解题速度减慢.完成后，学生回答.

生1：我发现第6题中的每个数都比第4题中的数少1，于是它的规律是n2-1.

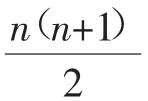
生3：我发现第7题中的数的规律很简单，就是n（n+1）.

师：同学们，你们发现了吗？这7道题中的数，我们都可以用字母表示出它们的规律，那就还可以用函数思想解决这种题目啊！

生4：哦，我明白了，把这些数设为y，把n当作自变量，当我找不到规律时就可以利用待定系数法解决了！

师：接下来我们试试吧.

【初探数式规律】

观察下列等式：

……

按上述规律，回答以下问题：

（1）用含n的代数式表示第n个等式：an=______；

（2）a1+a2+a3+…+an=______.

教师适当总结解题锦囊：

编序号—找“关系”—验证.

【再探图形规律】

例题教学：如图1，自左至右，第1个图由1个正六边形、6个正方形和6个等边三角形组成；第2个图由2个正六边形、11个正方形和10个等边三角形组成；第3个图由3个正六边形、16个正方形和14个等边三角形组成……按照此规律，第n个图中正方形和等边三角形的个数之和为______.

学生观察、计算，教师板书：①6+6=12，②11+10=21，③16+14=30.

生1：我发现正方形的个数是6+5（n-1），等边三角形的个数是6+4（n-1），所以个数之和是12+9（n-1）=9n+3.

生2：我发现后面一个数都比前一个数大9，所以规律是12+9（n-1）=9n+3.

生3：我用刚刚老师提到的函数思想试了一下，设个数和为y，函数解析式为y=kn+b，然后将（1，12）和（2，21）代入，解出解析式为y=9n+3，然后用（3，30）验证了一下，发现解析式是正确的.

师：同学们思考出了很多解题方法，有的一眼就能看出，一下子看不出来时也可以考虑利用函数思想.不过一定要记住最后一步要验证哦！

探囊取物：

如图2，图（1）是一个水平摆放的小正方体木块，图（2）、（3）是由这样的小正方体木块叠放而成的，按照这样的规律继续叠放下去，至第7个叠放的图形中，小正方体木块总数应是（ ）.

A.25 B.66 C.91 D.120

学生独立思考，大部分学生学会先编序号，然后找关系，而不是一头雾水，无从下手.教师让学生回答解题方法时，很多学生积极回答问题.

生1：我发现各数依次是1、1+5、1+5+9，即1、1+1+4=1×2+4×1、1+1+4+1+2×4=1×3+4×（1+2）、…，那么第n个数就是n+4×［1+2+…+（n-1）］=n+2n（n-1）=2n2-n.

生2：我是用函数思想解答的，我发现这几个数之间的变化符合二次函数，因此设函数解析式为y=an2+bn+c，然后分别将（1，1）、（2，6）、（3，15）代入，得到函数解析式是y=2n2-n.

师总结：所以我们以后碰到找规律题目时可以先编号，然后通过观察数之间的内在规律或用函数思想解决.

这时，一学生举手，说自己还有另外一种方法：我利用之前一道找规律题目（如图6）找到了灵感.观察，发现规律：1+3=22，1+3+5=32，1+3+5+7=42，…，则1+3+5+…+（2n-1）=n2.我观察这几个图形的主视图和左视图发现它们正好符合这个规律，然后把主视图和左视图重复相加的部分n减去就可以了，因此这道题的规律就是2n2-n.

图6

笔者、听课的老师和全班学生无一不为之惊讶，都为其热烈鼓掌，课堂气氛达到高潮.

师：我们都学会如何解决找规律问题了，接下来，大家来试试第三种类型吧.

【三探坐标系中的规律】

如图5，正△ABO的边长为2，O为坐标原点，点A在x轴上，点B在第二象限，△ABO沿x轴作无滑动的翻滚，经一次翻滚后得到△A1B1O，则翻滚3次后点B对应的点的坐标是_____，翻滚2017次后AB的中点M经过的路径长为_____.

四、二次评课

第二次的教学设计修改，得到备课组老师一致好评.这节课充分体现了教学相长的思想，教师在讲授知识的同时与学生互动，学生也参与到教学活动中积极思考和热烈讨论，在这一过程中老师和学生都学到了新的技能和方法.

五、课后反思

在初中数学中，探索事物间的数量关系或变化规律是重要内容，探索和理解简单的数量关系，探索和理解运算律，探索和理解具体问题中的变化规律等，这些都是初中生要掌握的知识，因此培养和发展学生探索规律的能力十分重要.在本节课中，笔者着重从以下几个方面进行教学设计：

1.夯实学生的学习基础

在学生初中三年的数学学习中，找规律题目出现的频率较高，学生对其的熟悉度较高，但题型较多，学生难以找到解决问题的方法和技巧.因此在教学之初，设计几个较简单的找规律题目，学生在做题的同时，加深对找规律题的认识和理解，夯实学习基础，易于接受知识点，为后续的教学活动做准备.

2.给学生提供合适的素材

在经历第一次课的失利后，笔者深刻反思，课堂素材较多，较繁杂，计算量大，限制了学生的思考.经过修改，课堂素材精简，在教学之初呈现较简单的找规律题目，学生在做题的同时发现解题技巧；在学生发现解题技巧后，呈现一道数式规律题，学生在完成题目的同时，通过师生的交流和展示，学会运用多种技巧和方法解决问题；接下来依次呈现两道图形探索规律题，学生解题兴趣浓厚，急于运用自己刚刚学到的方法解决，并在完成题目后获得成就感.

3.积极启发学生的思维

在小试身手环节，当学生面对较难题目时，适当指导学生观察前面几道题中数的规律，寻找数之间的内在规律，在学生展示后适当提到函数思想.共同完成两道题的解决后，有学生发现并运用了函数思想解题，这时笔者提出函数思想，并适时提醒学生这种方法的好处及与其他方法的不同，拓展学生的解题思维.在学生想到新的解题策略时，为之鼓掌，表扬其发现问题、总结问题的好习惯，使学生在学习过程中积极动脑思考、及时总结和反思，促进学生更好地发展.

4.注重学生的自我展示

比较两次课程设计，后者较重视学生的自我展示，学生在课堂上真正“有话可说”“有话能说”“有话想说”，成为课堂真正的主人，自主掌握自己的学习，并在学习过程中积极思考问题、参与课堂、学有所获.

教学，顾名思义是教师的教和学生的学，是教师和学生之间的互动过程.离开学生的主动学习，课堂就会变成教师的“一言堂”，也就失去了教学的魅力，因此教师的教学应适合学生发展，基于学生基础，启发学生思考，调动学生学习的积极性，这样才能在课堂上使学生真正参与到教学活动中，做到“有话可说”.