以寻找思路为核心：教学生“学解题”——从习题教学案例说起

☉江苏省苏州市吴江区松陵第一中学 蒋骏哲

一、写在前面

近读南京师范大学涂荣豹教授新著《数学教学设计原理的构建——教学生学会思考》，涂教授关于数学解题教学的原理有如下论述：数学解题教学的任务，实际上是要教学生“学解题”，而现实中的解题教学大多是“叫”学生“解题”，或者是给学生“讲”解题，并没有把解题教学落到教学生“学解题”上.其实学生的主要任务并不是解题，而是“学解题”.笔者深有同感，本文结合近期解题教学课堂上习题教学的案例，阐释自己的一些实践与思考.

二、习题教学案例

案例1：促进学生积累基本图形及性质.

例1如图1，在直角三角形ABC中，∠ACB=90°，CD⊥AB，垂足为D，BF平分∠CBA，交CD于点E，交AC于点F.若BC=3，AC=4，求CE的长.

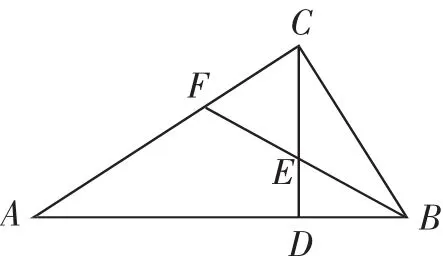
图1

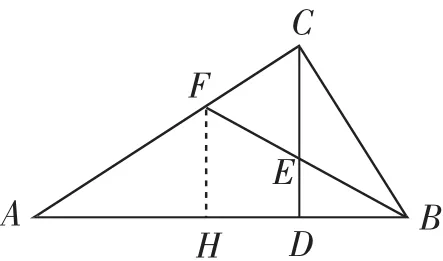
图2

教学记录：经过5分钟的独立思考后，多数学生只能求出AB=5，CD=2.4，后续没有获得进展.为了启发学生思考，我们不急于告知答案，也没有安排个别已获得答案的学生上台展示，而是给出以下几点思路启发：

念头1：该图形中有一个等腰三角形，先找出来并证明；

念头2：角平分线BF会启发哪条重要辅助线？

念头3：构造辅助线后，是否得到一个新的直角三角形？该直角三角形的三条边能否用一个未知数x表示不同边长，进而根据勾股定理列出方程求解呢？

很多学生经过这三个念头的启发，很快就发现等腰三角形CEF，于是待求的CE转化为CF，进一步在图2中作出FH⊥AB，从而将目光聚焦到直角三角形AFH中，利用勾股定理获得一个方程，实现问题求解.

解后回顾与反思：解答之后，提醒学生以后遇到类似的看似没有思路的几何题，要学会自己向自己提这样的方向性念头.另外，要求最初没有顺利解出的学生整理记录，并分解两个基本图形进行整理：

基本图形1：直角三角形中锐角平分线+斜边上的高，一定会出现等腰三角形；

基本图形2：角平分线的“比例”性质，如图1中，CF∶AF=BC∶AB.

教学随感：提示思路、促进解题者自己发现思路并贯通解题过程，而不是告知答案.前者是专业教师的“善于提问”“善于引导”的基本功，后者只是针对这一道习题的解法展示.此外，解题能力强的学生往往是积累、收集、记忆、储存这类基本图形及性质多的学生.所以，优秀解题者遇到这种基本图形出现时，就条件反射地有了方向或思路.

案例2：翻折问题的多角度思考.

例2如图3，将正方形纸片ABCD沿MN折叠，使点D落在边AB上，对应点为D′，点C落在C′处. 若AB=6，AD′=2，求折痕MN的长.

教学记录：这是八年级的一道练习题，八年级学生学过勾股定理、平行四边形的有关知识.学生经过5分钟独立思考后，没有获得最终解答.部分学生的进展是求出了AM、DM的长.我们通过对话追问了不少优秀学生的障碍，他们都把目光投向了右侧一些直角三角形中，但是苦于缺少条件，无法进展下去.为了帮助学生寻找思路，我们提供如下的启发性念头：

念头1：在你们思考的基础上，如果有八年级相似三角形的知识，也能够顺利继续前行……目前此路难通；

念头2：可另辟方向，如考虑翻折对称，连接DD′，能不能求出它的长度？

念头3：容易想到线段DD′与MN的位置关系吗？它们之间有怎样的数量关系呢？如能攻克，则大功告成！

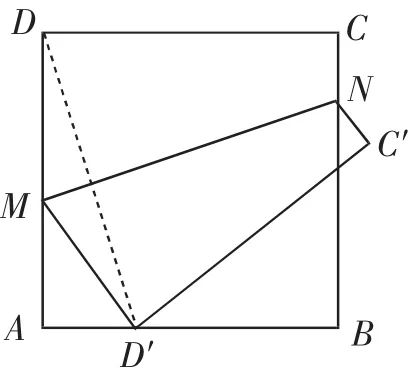
图3

学生在上述思考的启发下继续思考，不到3分钟，就有好几名学生贯通了思路，笔者请他们上台讲解思路，待一名学生讲解之后，有一半以上的学生都想通了思路.

案例3：双角平分线与平行线综合问题.

例3如图4，AM//CN，点B为平面内一点，AB⊥BC于点B，过点B作BD⊥AM于点D，E、F在DM上，连接BE、BF、CF.若BF平分∠DBC、BE平分∠ABD，∠FCB+∠NCF=180°，∠BFC=3∠DBE，求∠EBC的度数.

教学记录：学生经过5分钟的独立思考，基本没有进展.通过对话追问几个优秀学生，他们都觉得条件太多，感觉无从下手，只解读出几个看似不太有用的结论.于是，为了促进学生学会思考，我们提供如下念头：

念头1：求∠EBC的关键是求哪个角？能否设这个角为α，便于后续推理演算？

念头2：把目光投向顶点B处的一些角，这里双角平分线BE、BF的夹角是多少度？结合以前积累的一些基本图形及解题经验，能否直接看出它的角度？

念头3：用含α的式子分别表示∠ABD、∠BCN、∠FCB、∠BFC、∠FBC的度数；

念头4：可以选择在三角形BCF中，利用三角形内角和得出关于α的方程，获得解题思路的贯通.

经过上述念头的启发，一些优秀学生在5分钟后就贯通了思路，想清了在△BCF中，∠FBC=45°+α，∠BFC=3α，∠FCB=90°-α，于是利用三角形内角和得出α=15°，从而求得∠EBC=105°.

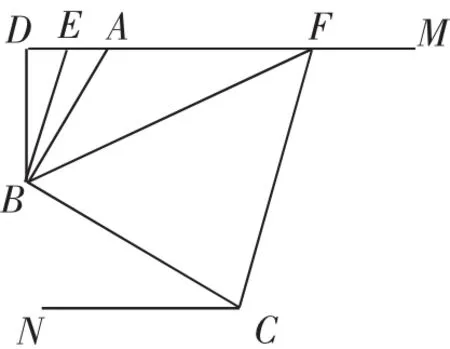
图4

三、教学生“学解题”的几点思考

1.理解习题结构，预设启发式提示语

教师在解题教学备课时不只是贯通思路、解出答案，而且要在此基础上想清习题的深层结构，对于较难习题还可辨析哪些步骤是关键步骤，有哪些可能的易错点，在此基础上预设一些启发式提示语，像上文中提供的一些念头启示都不是解题现场即兴想出来的，而是课前就有充分的预设，当学生出现障碍时就可适当给出，这样可提高课堂教学效率.另外，启发式提示语要注意引导学生“回到习题”，学会审题，对一些关键条件充分解读、关联不同条件组合解读，以便得到解题念头.

2.基于理解学生，预设铺垫式提示语

促进学生寻找思路的解题教学在理解习题结构的前提下，还要充分理解待教学生的学情，包括整体班情、个别优秀学生的思维能力与层次水平，这样在预设一些铺垫式提示语之后，要有相应学生能积极跟进，以便教学对话顺利进行，一些学生率先跟上教师铺垫式提示语之后，可安排他们上台讲解思路，让更多学生能跟上思路.如果学生整体理解能力不强，则铺垫式问题要更加“密集”，跨度不能太大，要让学生在铺垫式问题的提示之下，能获得进展，这样学生才能通过解题收获解题信心，有兴趣参与解题、跟进思考、“接力”思路进展.

3.引导回顾反思，想清习题关键步骤

波利亚在名著《怎样解题》中倡导解题教学要重视解后回顾与反思，在这个教学环节中，教师可以引导学生想清解题的关键步骤，一些易错点，一些容易看漏的条件信息，哪些是容易挖掘不深的条件，哪些条件可以组合、关联起来助推思路进展，等等.如果习题中有很多基本问题或基本图形存在，还需要引导学生分离、收集、积累这些基本图形及其性质，以便后续处理一些复杂问题时遇到这类基本图形及性质能快速识别，获得进展.

四、写在后面

解题是学习数学的重要组成部分，解题教学是数学教学的重要内容之一.如何开展解题教学是数学教学研究中的基本课题、日常课题，很多名师、专家都对解题教学投入大量精力进行研究，并形成了解题教学的诸多流派（如张景中院士倡导的“中巧说”、傅学顺教授倡导的“反应块”思想、顾泠沅教授总结的“变式教学”等）.对我们一线教师来说，重要的不是“选边站队”，而是要通过恰当的教法，远离题海战术，春风化雨，带领学生通过解题学会解题，悟得解题经验，提高解题智慧，发展数学思维.