培养探究问题能力，提升学生数学素养——以“反比例函数的图像与性质（二）”教学设计为例

☉江苏省苏州学府中学校 谢东莉

多年来，笔者一直坚持在教学第一线，一直致力于培养学生探究问题的能力，并取得了一定的成果.前不久，笔者在公开课展示活动中，开设了“反比例函数的图像与性质”一课，收到了广泛的好评，现整理成文，在此与各位同仁交流、研讨.

一、解读数学素养

数学素养，是指我们用数学的观点、思维方式和方法去观察、分析、解决问题，培养学生的数学意识、数学醒悟、数学思维习惯等.数学是一门知识结构有序、逻辑性很强的学科，数学知识的学习必须遵循学科特性，学习的过程是一个知识不断积累的过程，是一个知识运用和内化的过程，又是一个数学品质的培养过程，这就需要我们在平时的课堂教学中不断渗透，在每一节课、每一次教学中，提升学生的数学素养.

二、教学设计

课题：反比例函数的图像与性质（二）.

1.教学目标

（1）通过观察反比例函数的图像，类比正比例函数的性质，探究反比例函数的图像和性质.

（2）体会类比、分类讨论、从特殊到一般及数形结合的数学思想.

2.教学重、难点

反比例函数的图像和性质.

3.教学过程

（一）温故知新.

（1）回顾正比例函数y=kx（k≠0）的性质.

学生活动：填表1.

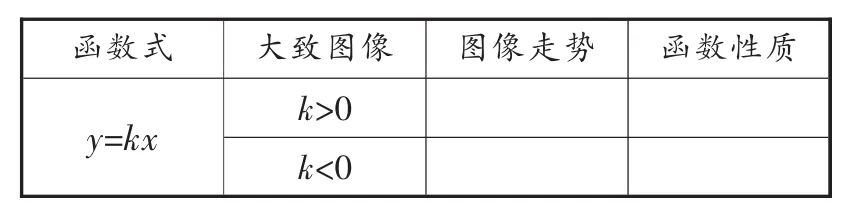
表1

（2）反比例函数的定义.

设计思路：在学习反比例函数的性质前，学生已具备了研究一次函数、正比例函数的经验，知晓了反比例函数的定义.类比这两类函数的学习方法，将这些知识和经验作为研究反比例函数图像和性质的认知起点和活动经验，只有把研究一次函数和正比例函数的学习经验迁移到反比例函数的图像和性质中来，学生的活动经验才会在这个建构的思维中产生正能量，学生才能在学习活动中形成并积累发现问题、提出问题、分析问题、解决问题的新能力和新经验，才能实现数学教学的终极目标.

（二）探究新知.

【活动1】

图1

（2）几何画板展示.

归纳：当k＞0时，（1）函数图像分别位于______象限；

（2）在______，y随x的增大而______.

练习：已知点A（-2，a）、B（-1，b）、C（3，c）都在反比例函数y=的图像上，试比较a、b、c的大小.

设计思路：此处设计让学生动手画反比例函数的图像，结合一次函数的图像和性质的研究方法，感知反比例函数的对称性、增减性和数据的无限性等特性，最后引导学生描点画图，展示图像，合作讨论得出性质.

设计理念：数学教学不能只停留在告诉或传递给学生静态的数学知识，而应尽可能地使学生获得怎样探求新知识的智力价值和智慧价值，这才是数学教学的根本之所在.

【活动2】

归纳：当k＜0时，（1）函数的图像分别位于______象限；

（2）在______，y随x的增大而______.

设计理念：运用类比的思想，研究k＜0时反比例的函数图像和性质，更容易掌握.

【活动3】归纳总结.

表2

（2）反比例函数图像的渐近性.

（3）反比例函数图像的对称性.

设计理念：注重小组合作，在探究中归纳，在类比后总结，通过填表格、画图像、对图像的研究和分析，让学生自行总结反比例函数的性质.

（三）应用新知.

（1）判断正误.

②已知点A（-3，a）、B（-2，b）、C（4，c）均在y=-的图像上，则a＜b＜c（.）

③反比例函数图像若过点（a，b），则它一定过点（-a，-b）（.）

（2）选择题.

①已知函数y=（m+1）xm2-5是反比例函数，且图像在第二、四象限内，则m的值是（ ）.

②已知（x1，y1）、（x2，y2）、（x3，y3）是反比例函数y=的图像上三个点，且x1＜x2＜0，x3＞0，则y1、y2、y3的大小关系是（ ）.

A.y3＜y1＜y2B.y2＜y1＜y3C.y1＜y2＜y3D.y3＜y2＜y1

设计意图：通过一组练习的设计，一方面巩固对知识点的掌握，另一方面，也提升了学生运用新知解决问题的能力.

（四）作业设计.

必做题：第49页第5题和第7题.

这两题都是反比例函数的应用，在学生掌握了反比例函数的性质和图像的画法后，才能给出正确的答案.

图2

设计意图：不同类型学生的接受能力有着明显差异，通过分层作业的布置，让不同的学生在数学学习上有不同的发展.

三、教学反思

这节课的教学设计，有如下四方面特点：

1.准确定位学生已有的知识和经验

本节课的教学设计，从已有的知识和经验出发，学生列表、画图，教师运用信息技术动态展示图像，揭示图像所承载的函数特征，让学生亲历了知识形成的过程，整体感知了函数的学习方法，通过学生积极思考实现元认知，既高效地使学生理解了教学的重点内容，又让学生亲历了知识产生的数学活动.

2.恰当地渗透数学思想

反比例函数的图像和性质，本身就是“数”与“形”的统一体.通过对图像的分析研究，让学生初步感知图像的分布区域和走向，可以确定函数本身的性质，这样从“数”想象“形”，从“形”研究“数”，体现了数形结合思想方法；通过类比一次函数的学习，研究反比例函数的图像与性质，体现了类比思想；将函数中变量x、y之间的对应关系，通过列表表达出来，对表格的解析也体现了函数的对应思想；通过画特殊反比例函数的图像，归纳总结反比例函数的图像和性质，体现了从特殊到一般的思想等.

3.合理地安排学生的数学活动

思维往往是从动手开始的.在教学中，引导学生用多种感官参与到知识的生成过程中，注重小组合作能力培养，教学中多次抛出问题，让学生分组讨论，交流展示成果；注重了学生动手操作能力的培养，通过让学生填表格、画图像，给学生较多的动手机会，学生充分参与，效果明显.

4.有效地设计作业

每个学生之间都存在着个体差异、智力差异、学习基础差异、学习品质差异.这些差异导致初中生学习数学存在两极分化现象，对于相同的教学内容会有不同的掌握程度，这就要求教师有必要根据学生的数学基础、智力水平及学习的主动性，分层布置作业.

四、写在最后

数学课堂的教学设计，不能只注重形式而忽略知识迁移从而失去本真，需要不断引导学生根据已有的知识和经验、学习方法，进一步对新知进行研究，不断引导学生体会事物是有规律的变化着的观点，用科学的方法解决问题，帮助学生了解数学模型的应用价值，培养学生科学的态度与精神，从而增强学习数学的自信心，发展数学能力，提升数学素养.素养的形成，不能单纯依赖教师的教，而是需要学生参与其中的数学活动；不能单纯依赖记忆与模仿，而是需要感悟与思维；它应该是日积月累的、自己思考的经验的积累.因此，基于核心素养的教学，要求教师抓住知识的本质，创设合适的教学情境，启发学生思考，让学生在掌握所学知识和技能的同时，感悟知识的本质，积累思维和实践的经验，形成和发展核心素养.