改编例、习题：让“教教材”走向“用教材教”——以人教版八下教材例、习题改编为例

☉江苏省海安市海陵中学 吴 晶

钟启泉教授指出：“用教材教”与“教教材”是区分新、旧教学的分水岭.所谓“教教材”，就是指那种照本宣科的讲课本，讲例、习题，而“教教材”则需要对教材内容进行深度理解.具体研读教材的角度很多，我们见到的很多文献中关于教材解读侧重于对数学知识引入、呈现或前后贯通的研究，针对教材上例、习题的改编研究则不是很多.本文结合具体的教材例、习题改编案例，阐释我们的做法与思考.

一、教材例、习题改编案例

案例1：“海伦-秦九韶公式”习题改编.

教材以“阅读理解”介绍了著名的“海伦-秦九韶公式”，并配一道习题：

在△ABC中，BC=4，AC=5，AB=6，请用海伦-秦九韶公式求△ABC的面积.

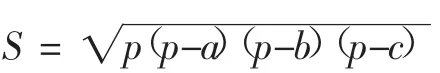
这个知识点非常重要，不但是数学文化的教育与熏陶，而且在各级考试中经常作为命题热点，所以在期中考试、期末考试复习时仍然要进行训练.但到了期中、期末考试时，不能像新授二次根式阶段一样教学，而应该与不同单元的数学知识进行综合，比如，将该知识点与勾股定理综合起来，可以改编如下：

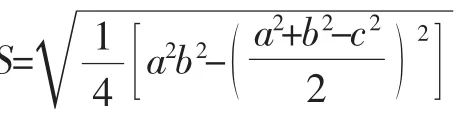
设计意图：这道习题引导学生复习秦九韶公式，然后运算之后的讲评环节可以引导学生再利用海伦公式算一次，比较不同公式的一致性.思维深刻的学生可能会发现这三边长恰能围成一个直角三角形，于是可以利用勾股定理逆定理判定直角三角形，再直接利用两条直角边的乘积的一半来快速解出该三角形的面积，训练学生思维的灵活性.

案例2：共顶点双等腰直角三角形问题.

教材上勾股定理习题中有如下一道共顶点的双等腰直角三角形问题：

如图1，△ACB和△ECD都是等腰直角三角形，CA=CB，CE=CD，△ACB的顶点A在△ECD的斜边DE上.求证：AE2+AD2=2AC2.（提示：连接BD）

解法简析：该题比较经典，在八年级上学期学习全等三角形时就在不少教辅资料上进行了比较泛滥的训练，一方面说明教辅资料的超前训练，另一方面说明这类问题更本质的是考查全等三角形的判定，当然，这类习题也是网络上有些人总结的所谓“手拉手模型”.那么，该如何发挥这道习题的教学功能，追求做一题、会一类、通一片的教学效果呢？我们给出如下改编：

教材改编题2：如图1，△ACB和△ECD都是等腰直角三角形，CA=CB，CE=CD，△ACB的顶点A在△ECD的斜边DE上.

（1）连接BD，求∠BDC的度数.

（2）若AE=3，AD=4，求AB的长.

（3）求证AE2+AD2=2AC2.

（4）探究线段AE、AD、BC之间的数量关系，并说明理由.

（5）设CE=5cm，分析四边形ACBD的面积是否变化.如果变化，指出它的面积最大值；如果不变，请说明理由.

改编意图：通过上述5个系列问题，可以让学生对这个基本图形可能的一些设问都有所训练，对图形中线段与线段之间的关系、角与角之间的关系、不同三角形之间的关系等都有较全面的研究，实现做一题、会一类的教学效果.另外，从九年级圆的角度来看，该题中四边形ACBD的四个顶点都在同一个圆上，将来可以站在更高的视角来理解这个问题的结构，在圆的教学过程中或中考复习阶段，仍然值得把这个图形进行改编开发成系列问题，发挥一题多练的教学功能.

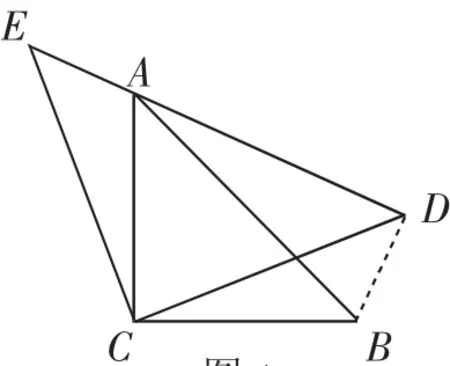
图1

案例3：折叠黄金矩形.

教材在平行四边形一章的数学活动中安排了折叠黄金矩形，限于篇幅，这里不链接该题（该题在不少地区期末考试、中考试题中都曾出现过）.以下只是针对该教材活动给出系列设问，如下：

问题1：图形中只有一个黄金矩形吗？为什么？

问题2：在图形中能否再折叠一次，得到一个60°的角？

改编意图：这两个问题可将探究成果扩大，并关联教材上另一个数学活动“折纸做60°、30°、15°的角”，有利于学生将所学内容关联起来，也是践行郑毓信教授提出的“数学知识不求多，而求联；数学习题不求难，而求变”.

案例4：研究绝对值函数.

教材在一次函数一章的习题中初步给出了绝对值函数，如下：

（1）画出函数y=|x-1|的图像.

（2）设P（x，0）是x轴上一个动点，它与x轴上表示-3的点的距离为y，求y关于x的函数解析式，并画出这个函数的图像.

教学组织：这道题的两小问之间看似条件互不关联，但是第（1）问给第（2）问提供了解法指导，起到了预热、铺垫作用.教学时，要充分利用这种铺垫式问题，在学生处理第（2）问遇到困难时引导学生退回到上一问，思考解题方向.在此之后，可给出如下变式问题：

设Q（0，t）是y轴上一个动点，它与点（0，-3）的距离为s.

①求t的函数s的解析式；

②直接写出该函数图像的最低点坐标：_______.

改编意图：从x轴变式到y轴上一点，并利用绝对值函数的图像分析最低点，对教材习题进行巩固和拓展，让学生初步感受绝对值函数的一些性质.

二、改编教材例、习题的几点思考

1.明辨教材例、习题的教学价值与地位

旅美数学教育学者马立平博士所指出的深刻理解数学知识经由郑毓信教授推介之后，得到不少同行的积极响应，近些年在不少课例研究、命题研究的文献中都能看出研究者们对深刻理解数学知识的追求.我们关于改编教材例、习题的做法也是基于深刻理解初中数学知识的基础上进行的，比如，教材上例、习题很多，改编时如何取舍呢？需要站在初中阶段数学知识的深刻理解的高度进行选取.比如，上文案例1中，我们选定了海伦公式作为改编，同时关联了勾股定理的逆定理，这些内容（二次根式的化简与运算、勾股定理）都是初中阶段的核心知识，同时渗透了数学文化.案例4中绝对值函数虽然不是初中阶段的核心知识，但是改编习题主要是让学生对点到点的距离公式、函数概念、函数研究方法有深刻理解和灵活运用.

2.变式改编要源于教材又高于教材

选取教材例、习题进行变式改编，要源于教材又要高于教材.具体来说，有些考题明明与教材无甚关联，却被有些命题者贴上源于教材的标签.而像上文中的几个题例，都是教材中明确存在的习题或活动素材，这里针对它们的改编就不止于再练一次，重复训练，而是在原题的基础上变式拓展、成果扩大、走向一般.比如案例2，不仅有效训练了共顶点的双等腰直角三角形带来的性质，同时将这个基本图形可能的命题考查方向都带领学生进行充分的探究，并且关联着后续圆的知识.再比如案例3，教材只是研究折叠出一个黄金矩形，而我们再次引导学生发现图形中还有另一个黄金矩形，这也是改编习题要“高于教材”的具体追求.

3.变式改编重在引领学生想深、学透

践行教材例、习题变式与改编是研究教材的一种重要方式，而不是“另选”（更多的是快速从一些资源网站直接下载、复制而来）大量与教材无关的所谓中考试题、名校模考试题.其目的是引领学生想深、学透，实现教材资源教学价值的更大化的一种追求.“郑毓信教授倡导的数学知识不求多而求联，数学习题不求量而要求变”，以及通过例、习题教学，促进学生想深、想透，都是我们变式改编例、习题的努力目标.

三、写在后面

教材研究是经典教研课题，我们选择改编例、习题的研究方式才刚起步，还有待深入，文中提及的一些题例打磨还不够充分，期待更多同行参与研讨，加深我们对改编教材例、习题的认识.