平面图的各种染色综述

吴建良， 杨东雷， 杨 帆

(山东大学 数学学院， 山东 济南 250100)

本文考虑的是简单无向图.有关概念和术语可以参考文献[1-2]，染色方面的书籍有文献[3-6]，一篇关于平面图染色的英文综述见文献[7].图一般由它的点集和边集组成.首先第1节介绍平面图的概念及其结构性质, 介绍几个特殊的平面图; 第2节介绍只染点方面的染色概念并综述部分染色在平面图方面的结果; 第3节介绍只染边方面的染色,并综述一些染色在平面图方面的结果; 第4节介绍图的全染色,列表全染色, 邻点(和)可区别的全染色, 无圈全染色等概念并叙述平面图相关的结果; 第5、6节首先介绍一些前面没有提到的染色, 罗列一些主要结果,并提供一些可以继续研究的问题.

1 平面图及其结构性质

如果一个图可以画在一个平面上使得它的边仅在作为公共端点的顶点处相交, 那么这样的图称为可平面图, 这种画法称作该图的一个平面嵌入. 在后面说到平面图时都默认为把平面图已经嵌入到平面上了. 这样平面图的边把平面分割成许多连通的区域, 我们把这些连通的区域称为面, 用F(G)(简记为F)表示图G的面的集合.

设X是一个固定的图. 在X中的一些边上插入若干新的顶点，这样所得到的图叫做X的细分(Subdivision). 换句话说，就是把X中的一些边换成长至少为2的路. 如果一个图G不包含X的任何一个细分作为子图,则称G是X-SF-图(X-subdivision-free graph). 用SF(X)来记所有X-SF-图的集合.

如果图X可以由图G的一个子图经过一系列的收缩边而得到，就称X是G的一个子式(minor). 如果一个图G不包含X作为子式,则称G是X-MF-图(X-minor-free graph). 用MF(X)来记所有X-MF-图的集合. 显然有MF(X)⊆SF(X).

1930年Kuratowski(1)参见文献[2]中的定理4.4.6.就得到定理：一个图是平面图当且仅当它是不含K5和K3,3的细分作为子图的图,即平面图G∈SF(K5)∩SF(K3,3). 1937年Wagner得到了一个等价的定理：平面图G∈MF(K5)∩MF(K3,3).

以上两个结果虽然非常漂亮地刻画了平面图，但是很难得到平面图的结构性质.而平面图欧拉公式却给人们带来不少惊喜.著名的平面图欧拉公式表述如下：设G是一个连通平面图, 则

|V|-|E|+|F|=2.

对f∈F(G),用与面f相关联的边的条数(其中割边计算两次)称为面的度, 记为dG(f), 简记为d(f). 易知:∑v∈V(G)d(v)=∑f∈F(G)d(f)=2|E(G)|. 把欧拉公式写成如下形式：

∑v∈V(G)(d(v)-4)+∑f∈F(G)(d(f)-4)=-8

或

∑v∈V(G)(d(v)-6)+∑f∈F(G)(2d(f)-6)=-12

等.把左边括号内的值分别定义为点或面的初值ch.由于右边是个负数，点和边中肯定有元素的初值是负的.这个变形在研究平面图的染色问题时非常有用，因为如果某个染色结果不成立，可以通过从初值为正的元素传一些值给初值为负的元素，使得它们的值全部非负，这样就使得欧拉公式不成立，从而导出矛盾.

另外，平面图还有一些子类：系列平行图、外平面图、k-外平面图、k-边界平面图、Halin图等.这些图类有更好的结构性质，在染色方面的结果都做得比较彻底.

•系列平行图：不包含K4作为子式的图，也叫K4-MF-图.

•外平面图：不包含K4和K2,3作为子式的图. 外平面图的顶点都与无穷外面关联.

•k-外平面图：把外平面图记作1-外平面图.当k≥2时，把k-外平面图的无穷边界上的点都删除以后就得到(k-1)-外平面图.

•k-边界平面图：顶点落在至多k个面的边界上的平面图叫k-边界平面图.显然，外平面图就是1-边界平面图.

•Halin图：设G(V,E,F)是一个3-连通平面图.如果G去掉与无穷外部面关联的边后得到的是一棵树，则称G为Halin图.

2 平面图的点染色

2.1 染色定义

图的染色理论开始于四色问题. 图的正常点染色(Vertex coloring)是指用颜色1,2,…,k对图的每个顶点分配一个颜色，使得相邻的顶点染色不同，染色所用的最少颜色数k就称为图的点色数. 四色问题就是问平面图是不是4-可染的. 如果在正常染色的基础上加上某个条件，就可以得到如下染色：

•均匀染色(Equitable coloring): 对图的一个正常点染色，如果任何两个不同的颜色所染的顶点数至多差1，那么就称此染色是均匀的；最小的颜色数称为图G的均匀色数，记为=(G). 如果对最小的k使得对所有的整数t≥k，图G都存在一个均匀染色，这个k就称为G的均匀色阈值，记为≡(G).

•无圈点染色(Acyclic coloring): 对图的一个正常点染色，如果任何两个不同的颜色所染的点集合所导出的子图是一个森林, 那么就称此染色是无圈的；最小的颜色数称为图G的无圈点色数，记为a(G).

•线性染色(Linear coloring): 任何两个不同的颜色所染的点集合所导出的子图是一个线性森林.

•(p,q)-标号((p,q)-labelling)：相邻的顶点的颜色至少差p，距离为2的两个点的颜色至少差q. (1,0)-标号就是我们说的正常点染色.(1,1)-标号又叫2-距离染色.

•邻点可区别的点染色(Adjacent vertex distinguishing vertex coloring):任何相邻的两个点所对应的邻域的染色集合不同.

•邻和可区别的点染色(Adjacent sum distinguishing vertex coloring): 任何相邻的两个点所对应的邻域的颜色之和不相等.

•r-色调染色(r-hued coloring):度数为d的顶点邻域至少出现min{d,r}种颜色.

•邻域r-限制染色(Neighborhoodr-bounded coloring)：每个点的同色邻点数不得超过r个. 如果不要求正常染色，笔者有如下染色：

•(k,d)*-染色: 用k种颜色去染图的点使得染同色点集合的导出子图的最大度至多为d;

•点荫度和线性点荫度：用k种颜色去染图的点使得染同色点集合的导出子图是一个最大度至多为t的森林，所用最少的颜色数称为图的t-点荫度. 如果森林的最大度没有限制，即t为无穷大，就称为图的点荫度(Vertex arboricity),记为va(G)； 如果t=2, 就称为图的线性点荫度(Linear vertex arboricity),记为vla(G). 当然还有：

•圆染色(Circular coloring): 给一个周长为k的圆环L(k≥2),图G的每个点对应于L上长度为1的半开弧. 如果两个点相邻，它们对应的弧不交，就说G是k-圆可染的. 最小的k称为G的圆色数. 这个概念有几个等价的定义, 如: 假设1≤2d≤k, 如果用k种颜色给图的每个点一个颜色且存在某个染色φ使得任何相邻的两个点u,v都有d≤|φ(u)-φ(v)|≤k-d，则称G存在k/d-圆染色. 最小的k/d称为G的圆色数.

•分数染色(Fractional coloring): 用k种颜色给图的每个点染d种颜色. 如果任何相邻的两个点所染颜色的集合不交，则称G存在k/d-染色. 最小的k/d称为G的分数色数.

•(k,d)-可选的((k,d)-choosable): 如果给图G的所有点v都分配一个颜色集合L(v)(也叫色列表)且G存在一个正常的点染色φ使得对每个点v∈V(G)都有φ(v)∈L(v),则称图G是L-可染的. 如果对满足下列两条的任何色列表L：

(1)对任意的v∈V(G), 都有|L(v)|≥k，且

(2)对任意相邻的两个点u和v, 有|L(u)∩L(v)|≤d;

G是L-可染的，则称G是(k,d)-可选的, 也称G有一个(k,d)-列表染色. 最小的k称为G的d-可分离的列表色数如果k=d, 就把G是(k,d)-可选的简称为G是k-可选的, 也说G有一个k-列表染色. 最小的k称为G的列表色数list(G)，等等.

除了以上染色外，还考虑了把上述两个概念相结合得到新的染色概念，如：均匀列表染色、无圈列表染色、邻点(和)可区别的列表染色、圆点荫度、列表分数染色等.这些概念就不详细地给出定义了.

本节的其余部分将叙述平面图的点染色和列表点染色、点荫度和线性点荫度、均匀染色和均匀点荫度、无圈点染色、(k,d)-列表染色等方面的结果.

2.2 平面图的点染色与(k,d)-可选性

由四色定理可知，平面图是4-可染的，而4也是最好的界.接下来一个自然的问题就是：什么样的平面图是3-可染的？已知判断一个平面图是否3-可染是NP-完全的，因此寻找3-可染的充分条件也是该方向的一个重要研究课题.一个经典的结果是Grötzsch[8]在1959 证明了任意一个不含三角形的平面图是3-可染的.此外，如果平面图G不含5-圈且两个3-圈的距离至少为2[9]; 或者G不含5-圈, 7-圈和两个3-圈不邻[10]，那么G是3-可染的.

相较于点染色，平面图的列表染色要复杂得多.Voigt[11]构造了一些不是4-可选的平面图，Thomassen[12]在1994年非常漂亮而又非常简单地证明了每个平面图是5-可选的.目前这个结果已经推广到了K5-minor free图[13]以及局部平面图[14].

这样自然会有一个问题：哪些平面图是4-可选的，哪些是3-可选的？有关3-可选的第一个结果是由 Alon等[15]在1992得到的，他们证明了平面二分图是3-可选的.随后Thomassen[16]证明了围长为5的平面图是3-可选的.该定理的证明方法借鉴了5-可选的证明思路，而这个围长条件也是紧的[17].2009年Li[18]巧妙地证明了4-圈不与4-圈和5-圈相交的平面图是3-可选的，该结论推广了Thomassen的结果.以下列出平面图是3-可选的一系列充分条件：

•图G不含长度为4和9的圈，同时不含长度为{5，6，7，8}中任两数的圈[19].

•图G不含长度为3, 5, 6的圈[20].

•图G不含长度为4, 5的圈且任两个三角形距离至少为4；或者图G不含长度为4, 5, 6的圈且任两个三角形距离至少为3[21].

•图G不含长度至多为10且含一弦的圈[22].

•图G不含长度为3,7,8 的圈[23].

•图G中两个长度至多为4的圈的距离至少为26[24].

•图G不含长度在4至8之间的圈[25].

关于4-可选也有很系统的研究结果.运用欧拉公式很容易得出任何不含3-圈的平面图是3-退化的，因此也是4-可选的.Wang等[26]把此结果推广到了不含相交三角形的平面图. 关于平面图是4-可选的还有如下一些充分条件：①不含i-圈(i∈{4,5,6,7})；②不含相邻于三角形的4-圈；③每个5-圈不同时相邻3-圈和4-圈; ④不含相交5-圈; ⑤不含弦6-圈.

1998年Kratochvíl等[27]把列表染色概念扩充到了(k,d)-可选性(Choosability with separation), 并证明了平面图是(4,1)-可选的, 同时猜想平面图是(4,2)-可选的. 这个猜想对没有弦k-圈(k=5,6或7)的平面图是成立的.krekovski[28]指出存在无3-圈的平面图不是(3,2)-可选的，同时他猜想平面图是不是(3,1)-可选的? 目前平面图是(3,1)-可选的条件有：

•没有3-圈.

•没有4-圈.

•没有5-圈和6-圈.

•对5≤i≤6,5≤j≤7, 任何i-圈和j-圈都不邻.

2.3 均匀点染色和均匀点荫度

Hajnal和Szemerédi(2)Hajnl A, Szemerédi E. Proof of a conjecture of P.Erdös, in: P.Erdös A, Rényi VT, Sós (Eds.). Combinatorial Theory and its Applications, North-Holand, London, 1970： 601-623.在1970年证明了如下著名的定理: 对于任意的正整数r，任意一个最大度至多为r的图都存在一个均匀(r+1)-染色.对这一经典结论，2008年Kierstead等[29]给出了一个简化的证明，同时也给出了一个找此均匀染色的多项式时间算法.另一方面，早在1973年Meyer猜想(ECC)(3)Meyer W. Equitable coloring. American Mathematical Monthly, 1973，80: 920-922.: 如果图G不是Km,C2m+1, 那么存在一个r(≤Δ(G))使得G是均匀r-染色的.而Chen等[30]在1994年提出了一个加强版的猜想(EΔCC)：如果图G不是Km,C2m+1,K2m+1,2m+1, 那么G存在一个均匀Δ(G)-染色， 即≡(G)≤Δ(G).并且证明了当最大度Δ(G)≥3或者Δ(G)≥|G|/2时，该猜想是成立的.直到2012年Chen等[31]将结果改进到了Δ(G)≥|G|/3+1.

关于平面图的均匀染色，Yap和Zhang证明了对于最大度至少为13的平面图，EΔCC-猜想时成立的.到目前为止改进到最好的界是最大度至少为9的平面图[32].下面列出近些年已知的满足EΔCC-猜想的一些特殊平面图：①系列平行图；②Δ≥5且围长大于等于6的平面图; ③Δ≥6且不含三角形，或者不含4-圈和6-圈的平面图; ④Δ≥7且不含4-圈的平面图. 这几个结果有些在列表的情况下也是成立的，关于平面图的均匀列表染色还有不少结果.Wu等[33]证明了: Δ≥3且对围长至少为26的非二部平面图，或者围长至少为4的2-连通的外平面图，有≡(G)=(G).由此可以提出一个问题：什么情况下，均匀色数阈值等于点色数？2011年Fan等[34]证明了ECC猜想的一个松弛情况：任何简单图都存在一个均匀的非正常Δ-染色，使得每个颜色所染点的导出子图是一些孤立边. 随后，Wu等[35]提出了均匀点荫度的概念，并给出了猜想：①所有图的均匀点荫度至多为「(Δ+1)/2⎤; ②所有平面图的均匀点荫度不超过一个常数. 最近，Esperet等(4)Esperet L, Lemoine L, Maffray F. Equitable partition of graphs into induced forests. Discrete Math, 2015, 338(8):1481-1483.证明了：任何至少有两个点的连通图的均匀点荫度小于无圈点色数. 因为平面图的无圈点色数不超过5，所以由此推出：平面图的均匀点荫度不超过4，验证了猜想的第②部分.根据此结果，笔者猜想：平面图的均匀点荫度不超过3.

2.4 无圈点染色

无圈点染色是在正常点染色的基础上加强了限制：要求每个圈上都至少出现3种颜色.这个概念最早是由Grünbaum[36]提出的，同时他在文中证明了任意一个平面图是无圈9-可染的.经过了学者们的不断改进，最终Borodin[37]证明了任意一个平面图是无圈5-可染的，并且证明了5是紧的上界. 这个结果被Mohar[38]推广到了局部平面图上了.Kostochka等[39]也构造一个2-退化的二部平面图，不是无圈4-可选的.而Borodin等[40]证明了对于不含三角形的平面图，该结果可以改进到4，对于围长至少为7的平面图，可以改进到3.从计算复杂度的角度来看，Kostochka[41]证明了判断一个图是否是无圈k-可染的(任给k≥3)，还是NP-完全的.

考虑列表形式的无圈染色，Borodin等[42]证明了任意一个平面图都是无圈7-可选的，并且猜想：任意一个平面图都是无圈5-可选的.此猜想对两类特殊的平面图是成立的：①不含4-圈的平面图;②任意一个3-圈不邻{3，4，5}-圈并且4-圈不邻{4，5，6}-圈.一个平面图是无圈4-可选的，如果它满足以下任意一个条件：①围长为5;②不含{4，5，6}-圈；③不含{4，5，7}-圈；④不含{4，5}-圈以及相交三角形;⑤没有4-圈和三角化6-圈;⑥没有{4，5}-圈以及三角弦8-圈;⑦没有{4，7，8}-圈;⑧没有{4，5}-圈的平面图.Montassier等[43]猜想：不含4-圈的平面图是无圈4-可选的.而后Borodin等[44]证明了任意的3-圈不邻{3,4,5,6}-圈且4-圈不邻{4，5，6，7}-圈的平面图是无圈4-可选的.同时他们提出了问题：是否任意一个4-圈不邻(≤4)-圈的平面图都是无圈4-可选的？Borodin等[45]证明了围长为7的平面图是无圈3-可选的，而且他们也猜想:围长为5的平面图都是无圈3-可选的.

以下三个结果是非平面图的.

•任意一个环面图是无圈8-可选的[46].

•任意一个1-平面图是无圈20-可染的[47].

•所有的局部平面图是无圈7-可染的[48].

2.5 点荫度和线性点荫度

给定一个图G，令va(G)表示最小的整数k使得图G存在一个k-染色，其中每个色类的导出子图都是一个森林.作为图的正常点染色的弱化，这个概念是由Chartrand等[49]首先定义的.并且他们证明了va(G)≤max{(1+δ(H))/2:H⊂G}.由此可以推出：任何平面图G, 有va(G)≤3. Hakimi等[50]指出判定极大平面图的点荫度为2的问题都是NP-完全的, 同时他们证明了一个平面图的点荫度为2当且仅当它的对偶图(Dual graph)有一个连通欧拉支撑子图.平面图G的点荫度至多为2的充分条件有:①不含i-圈，其中i可取4、5、6中的任意一个;②任意两个3-圈距离至少为3；③两个3-圈不共点;④G不含弦6-圈;⑤5-圈不交;⑥5-圈不同时相邻于3-圈和4-圈.这些结果有些证明是列表情况.

图G的线性点荫度vla(G)的概念是由Harary[51]提出的，其要求每个色类的导出子图是一个线性森林(一些不交的路).Poh[52]证明平面图G的线性点荫度vla(G)≤3.

3 平面图的边染色

3.1 边染色方面的定义

图G的线图L(G)是指把G的边集作为L(G)的点集,L(G)中的两个点相邻当且仅当它们在G中的边相邻. 图G的正常边染色(Proper edge coloring)、无圈边染色(Acyclic edge coloring)、强边染色(Strong edge coloring)、(p,q)-边标号((p,q)-edge labelling)、 圆边染色(Circular edge coloring)、 分数边染色(Fractional edge coloring)、(k,d)-边可选的((k,d)-choosable)、列表边染色(List edge coloring)、无圈列表边染色(Acyclic list edge coloring)分别就是L(G)的正常点染色、无圈点染色、2-距离标号、(p,q)-标号、 圆染色、 分数染色、(k,d)-可选的、列表边染色和无圈列表边染色.所用最小的颜色数称为图G的边色数、无圈边色数、强边色数、(p,q)-边标号数、圆边色数、分数边色数、(k,d)-边可选数、列表边色数和无圈列表边色数，分别用′(G)、、和ac′list(G)表示.除以上边染色外，人们还研究了如下边方面的染色：

•邻点(和)可区别的边染色(Adjacent vertex(sum) distinguishing edge coloring): 对图G的一个正常边染色φ，令Cφ(v)={φ(uv):uv∈E(G)}和cφ(v)=∑uv∈E(G)φ(uv).如果任何相邻的两个点u和v，有Cφ(u)≠Cφ(v)，那么称此边染色为图的邻点可区别的边染色，最小的k称为图的邻点可区别的边色数，记为′adj(G)或′adj；如果任何相邻的两个点u和v，有cφ(u)≠cφ(v)，那么就称此边染色为图的邻和可区别的边染色，最小的k称为图的邻和可区别的边色数，记为或关于邻点(和)可区别的列表边色数，记为或

•均匀边染色(Equitable edge coloring): 对图G的一个边染色(不需要正常)，如果对所有的顶点，与它关联的边中任何两个不同的颜色所染的边数至多差1，那么就称此边染色是均匀的.

•(k,d)-荫度：用t种颜色去染图的边使得染同色的边导出子图是一个森林并且森林的每个连通分支的最大度至多为k和直径至多为d，所用最少的颜色数称为图的(k,d)-荫度. 如果k和d都为无穷大，(k,d)-荫度又称为图的荫度(Arboricity), 记为a(G)； 如果k=2且d为无穷大, (k,d)-荫度又称为图的线性荫度(Linear arboricity),记为la(G); 如果k=t=2, (k,d)-荫度又称为图的线性2-荫度(Linear 2-arboricity),记为la2(G).

以上这几个染色也均有列表情况.下面主要叙述以上几个染色在平面图方面获得的一些结果.

3.2 正常边色数

关于正常边染色，有著名的Vizing定理(参见文献[4-6])：对任何简单图G，有Δ≤′(G)≤Δ+1. 如果′(G)=Δ，则称G是第一类图，否则称G是第二类图.在平面图方面，还是Vizing首先证明：最大度至少是8的平面图是第一类图， 同时他还提出如下猜想(平面图的边染色猜想, ECC)：最大度至少是6的平面图是第一类图.Zhang[53]以及Sanders等[54]分别证明了此猜想在Δ=7的情况是成立的.所以此猜想只有Δ=6还没有被完全解决.关于平面图G是第一类的还有如下条件:

•Δ=6且满足以下条件之一：①每个点至多关联三个三角形；②不含弦k-圈，其中k∈{3,4,5,6,7}; ③任意5-圈至多包含1条弦；④任意6-圈至多包含2条弦;⑤任意两个7-圈不邻；⑥任意k-圈至多邻1个k-圈，其中k∈{3,4,5}.

•Δ=5且满足以下条件之一：①不含4-圈或5-圈；②任意3-圈与4-圈不邻；③每个点至多关联一个三角形.

•(Δ，g)∈{(5,4),(4,5),(3,8)},其中g是围长.

3.3 列表边色数

列表边染色的概念首先由Vizing[55]提出，而后Borodin等[56]提出了一个非常具有挑战性的猜想——列表边色数猜想：对所有的图G，有′(G). 显然′(G)≤对平面图，如果满足如下条件之一，此猜想就成立.

•Δ≥12[32].

•Δ≥10且①任何7-圈至多含两条弦，或②任何6-圈至多含一条弦.

•Δ≥8且满足以下条件之一：①不含弦5-圈；②4-圈不邻；③3-圈与4-圈不邻；④3-圈与5-圈不邻.

•Δ≥8且满足以下条件之一：①不含弦5-圈；②4-圈不邻；③3-圈与4-圈不邻；④3-圈与5-圈不邻.

•Δ≥7且满足以下条件之一：①4-圈与4--圈不邻；②同时不含5-圈和6-圈.

•Δ≥6且同时不含4-圈和6-圈.

•Δ≥5且g≥5或Δ≥4且g≥6或Δ≥3且g≥10.

•(Δ,k)∈{(7,4),(6,5),(5,8),(4,14)},不含长度从4到k的圈，其中k≥4.

同时对平面图G，满足充分条件如下：

•Δ≥8[57].

•Δ≥7且①任何7-圈至多含两条弦，或②任何6-圈至多含一条弦.

•Δ≥6且G满足以下条件之一：①3-圈不邻或不含7-圈；②3-圈与5-圈不邻；③不含弦5-圈；④不含弦6-圈；⑤4-圈不邻.

•Δ≥5且G满足以下条件之一：①同时不含弦5-圈和弦4-圈；②同时不含弦5-圈和弦6-圈；③3-圈和4-圈不邻；④不含5-圈.

•Δ≤4[58].

3.4 无圈边色数

同样，也可以将无圈边染色推广到无圈列表边染色，这方面的结果相对较少并且都是限制在特殊图类上，如外平面图[63]、Halin图的剖分[64]等.

3.5 强边色数

因为强边色数一般比较大,想获得强边色数的确切值是非常困难的.Erdös等[65]提出猜想:对任意图G，当Δ取偶数时，否则此猜想在Δ≤3的情况下是成立的.对最大度至少是3平面图, 一般的界是:下面主要介绍平面图的一些其他结果：

3.6 均匀边色数

如果和点染色一样，要求在正常边染色的基础上使得任何两个颜色染的边数之差不超过1，这个问题就变得非常容易了，因为Werra[67]已经证明了：如果一个图存在正常k-边染色，就一定存在这样的均匀k-边染色.所以均匀边染色的概念就变成了前面所给的定义，它要求在所有点的关联边里每个颜色均匀的出现.关于这方面的第一个主要结果是由Hilton等[68]获得的：设G是简单图且k≥2，如果G中的所有点的度均不能整除k,则G是均匀k-边可染的.2011年Zhang等[69]推广并证明了Hilton提出的一个猜想：设G是简单图且k≥2,如果G中的所有度数能整除k的点集合导出的是一个森林,则G是均匀k-边可染的.2017年Hu等[70]创造性地证明了：对任何至少为12的整数k，所有的平面图都存在一个均匀k-边染色.由于证明过程用到的都是以前的基本工具，所以他们提出猜想：对所有整数k(≥6)，任何平面图都存在一个均匀k-边染色.如果这个猜想成立，那么平面图的边染色猜想也是成立的.

2001年Wu[71]提出概念：如果对所有的整数k(≥1), 一个图G都存在一个均匀k-边染色，那么G就称为是均匀的.同时他证明：连通的外平面图是均匀的当且仅当它不是含有奇数个点的欧拉图.这一结果在2007年被Song等[72]推广成系列平行图.

3.7 邻点(和)可区别边色数

如果一个图包含只有一条边的连通分支，那么这个图是没有邻点或邻和可区别的边染色.因此本节都假设图不包含只有一条边的连通分支，这样的图称为正规图.邻点可区别的边染色问题是由Zhang等在文献[73]中提出来的，他们猜想(AVECC)：如果G是含至少6个点的连通图，则≤Δ(G)+2.同时他们验证了此猜想对树、圈、路、完全图以及完全二部图是成立的.2014年Horňk等[74]证明：如果G是正规连通平面图，则因为对任何图G, 有∑(G),所以下面的猜想(A∑ECC)推广了AVECC：如果G是正规连通图且G≠C5,则Δ≤在平面图方面，Wang等[76]证明了：如果G是正规连通平面图，则同时Bonamy等[77]证明了：对Δ≥28的正规连通平面图G，有′∑(G)=Δ(G)+1.此外，对一些特殊的平面图，也有一些相关的结果.

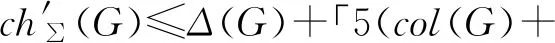
3.8 平面图的荫度、线性荫度、线性k-荫度以及列表情况

图G的线性荫度la(G)就是把G的边分解成线性森林的最少个数.关于线性荫度，有著名的猜想：所有图G的线性荫度满足la(G)≤「(Δ(G)+1)/2⎤[78]. Wu等[79-80]证明此猜想对所有平面图是成立的.吴建良[81]猜想(LAC, 此猜想也出现在文献[82]中)： 对最大度至少为5的平面图G, 有la(G)=「Δ(G)/2⎤. 此猜想对满足如下条件之一的平面图是成立的：

(1)Δ(G)≥9[82];

(2)Δ(G)≥7且①不含弦i-圈(i∈{4,5,6,7}),或②5-圈至多含一弦，或③7-圈至多含两弦，或④对任一点v∈V(G), 都存在两整数iv,jv∈{3,4,5,6,7,8}使得与v关联的两个长度分别为iv和jv的圈是不相邻的；

(3)Δ(G)≥5, 且①不含4-圈，或②不含相交的4-圈和相交的5-圈,或③不含带弦的5-圈和6-圈;

(4)Δ(G)≥3, 且图G的围长g≥6.

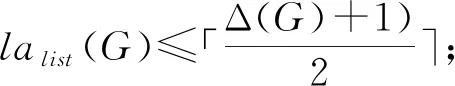
图G的线性k-荫度lak(G)是指G的边分解成长度不超过k的线性森林的最少个数.图的线性k-荫度最早是由Habib等[85]提出的，他们也给出了相应的猜想. 目前关于平面图的线性k-荫度的最好的界是由Wang等[86]给出的：对任何平面图G, 有la2(G)≤「(Δ(G)+1)/2⎤+6.另外，王维凡等在外平面图和不含4-圈的平面图上也获得了一些非常有价值的结果.

4 平面图的全染色

4.1 平面图的全染色和列表全染色

一个图的全染色是指对图G的点和边都染色，使得相邻和相关联的元素之间都染不同的颜色. 图G的全色数″(G)定义为图G的所有全染色中所用最少颜色的数量. 著名的全染色猜想为(TCC)[87-88]：任意简单图G，Δ(G)+1≤″(G)≤Δ(G)+2. 有关一般图全染色方面的结果可参见文献[5]. 对平面图, 此猜想只有最大度为6时没有完全证明. 2008年前经过好几篇文章的接力最终证明了：最大度至少为9的平面图G有″(G)=Δ(G)+1. 从而在2009年Shen等[89]提出了平面图的全染色猜想(Planar-TCC)：最大度为4到8之间的平面图G有″(G)=Δ(G)+1. 此平面图的全染色猜想是成立的，如果满足下列条件之一：

•Δ(G)≥8且对G中任一顶点x,都存在整数k∈{3,4,5,6,7,8}使x至多关联一个k-圈.

•Δ(G)≥8且对G中任一顶点x,都存在两整数i,j∈{3,4,5,6}使任意两个经过x的长度为i和j的圈都不相邻.

•Δ(G)≥8且①没有5-扇, 或②不含带两弦的5-圈, 或③不含相邻弦5-圈, 或④不含相邻弦7-圈, 或⑤不含带两弦的6-圈, 或⑥弦6-圈不相邻, 或⑦不含带3弦的7-圈.

•Δ(G)≥7且对G中任一顶点x, 都存在整数k∈{3,4,5,6,7,8}使x不关联任一个k-圈.

•Δ(G)≥7且对G中任一顶点v, 都存在整数iv∈{3,4,5,6}使v不在任一个iv-圈上.

•Δ(G)≥7且不含①弦i-圈, 这里i=5,6或者7, 或② 3-圈相邻于5--圈, 或③ 5-圈和6-圈, 或④相交3-圈, 或⑤相邻的4-圈和相邻的5-圈, 或⑥ 相交的6-圈.

•Δ(G)≥6且图G不含①相交的4-圈，或②相交的3-圈、5-圈或者6-圈, 或③ 4-圈, 或④相邻的4--圈.

•Δ(G)≥5且图G没有4-圈和6-圈.

•图G的最大度和围长(Δ,g)∈{(7,4),(5,5),(4,6),(3,10)}.

•(Δ,k)∈{(7,4),(6,5),(5,7),(4,14)}且图G没有长度在4至k之间的圈.

•(Δ,k)∈{(6,4),(5,5),(4,11)}，图G不含相交3-圈且没有长度在4至k之间的圈.

关于图G的列表全色数有猜想：如果G是一个简单图，则″(G)[56]. 这确实是一个非常有挑战性的猜想，目前对一般图的结果非常之少. 关于平面图，有两类结果. 一类是关于的，它需要有如下条件之一：

•Δ(G)≥9[90].

•Δ(G)≥7且①没有弦7-圈, 或②没有5-扇, 或③每个3-圈至多与其他一个3-圈相邻.

•Δ(G)≥6且不满足：①弦6-圈, 或②3-圈与5-圈相邻, 或③ 3-圈与4-圈相邻.

•Δ(G)≥5且没有：①弦5-圈和弦4-圈, 或②弦5-圈和弦6-圈, 或③ 3-圈或4- 圈, 或④ 5-圈.

•Δ(G)≥12[56].

•(Δ,k)∈{(7,4),(6,5),(5,8),(4,14)}且图G没有长度在4至k之间的圈.

•Δ(G)≥8且①不含弦5-圈, 或②不含相邻4-圈, 或③ 3-圈与4-圈不相邻, 或④ 3-圈和5-圈不邻.

•Δ(G)≥7且任4-圈不相邻于4--圈, 或者没有5-圈和6-圈.

•Δ(G)≥6且没有4-圈和6-圈.

4.2 邻点(和)可区别的全染色

用k种颜色对G的点和边进行一个全染色ψ, 用Cψ(v)来表示点v的颜色以及与v关联边的颜色集合. 如果对任何相邻的两个点v和u，都有Cψ(u)≠Cψ(v)，就称这种全染色是邻点可区别的，ψ称为G的一个邻点可区别的k-全染色, 并称G是k-邻点可区别全可染的.G具有k-邻点可区别全染色的最小的k称为图G的邻点可区别全色数, 记做在文献[91]中, Zhang等提出了这个染色的概念, 并研究了树、圈、轮、完全图、完全二分图等图的这种染色, 然后提出了猜想(称为邻点可区别的全染色猜想，简记为NVD-TCC): 对于至少有两个点的图G满足

Δ(G)+1≤

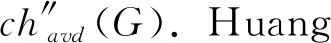
设G有一个用颜色1,2,…,k染的全染色ψ, 笔者用cψ(v)来表示点v的颜色以及与v关联边的颜色的和值. 如果对任何相邻的两个点v和u，都有cψ(u)≠cψ(v)，就称这种全染色是k-邻和可区别的，ψ称为G的一个k-邻和可区别全染色, 并称G是k-邻和可区别全可染的.G具有k-邻和可区别全染色的最小的k称为图G的邻和可区别全色数, 记做类似地可以定义图的邻和可区别全-k-列表染色和邻和可区别列表全色数记为邻和可区别全染色的概念是由Pilsniak等[97]在2015年提出的. 他们研究了圈、路、星、完全图、二分图以及最大度不超过3的图, 发现这些图的邻和可区别全色数都不超过Δ+3, 于是类似于邻点可区别全染色, 他们提出了猜想(称为邻和可区别的全染色猜想, NSD-TCC): 对于至少有两个点的图G, 有

Δ(G)+1≤

4.3 无圈全染色

给定图G的一个正常全染色ψ，如果任何一个圈上的点和边至少染了4种颜色，则称这种全染色为图的无圈全染色，最小的颜色数称为图的无圈全色数，记为无圈全染色的概念首先由Sun等[105-106]提出，并得到了平面图方面的一些相关结果.

5 与平面图的面有关的染色

下面的三个染色因为要对平面图的面进行染色，它们是平面图的专属染色：①平面图的点面染色：对平面图的点和面进行染色，使得相邻的点、相邻的面、相关联的点和面之间都染不同的颜色.所用最少的颜色数称为平面图的点面色数，记为vf(G)； ②平面图的边面染色: 对平面图的边和面进行染色，使得相邻的边、相邻的面、相关联的边和面之间都染不同的颜色.所用最少的颜色数称为平面图的边面色数，记为ef(G)； ③平面图的点边面染色: 对平面图的点、边和面进行染色，使得任何两个相邻或相关联的元素之间都染不同的颜色.所用最少的颜色数称为平面图的点边面色数，也叫完备色数，记为vef(G). 人们已经证明了：对任何平面图G，vf(G)≤6,ef(G)≤Δ(G)+3,vef(G)≤Δ(G)+4. 其他结果参见文献[7].

6 可以继续探讨的一些问题

今后可以继续研究的问题：

(1)改进现有结果，降低现有的上界，证明相关猜想或者得到一部分结果.例如，证明4-圈不交的平面图是列表4-可染的；

(2)考虑多种染色的组合，研究新的染色，获得比现有结果更一般的结果，例如，可以在考虑邻和可区别的边染色时要求相邻两点的色和至少差k(k>0)，或者在正常染色的基础上再要求增加一条边两个端点所关联的边中至多有k个相同色，等等.

(3)把相关的结果扩展到更一般的图类.人们知道利用平面图的证明思想，以上染色在1-平面图方面获得了许多优秀的成果，关于嵌入到曲面上的图和局部平面图也有不少研究，但有些染色在这些图类上的研究还是一片空白.另外，还可以考虑不含K5作为子式的图和不含K3,3作为子式的图.

后记： 限于篇幅，还有许多关于平面图的染色方面的结果没有列出，它们都是很有价值的，例如：圆染色(Circular coloring)、 多重染色(Multiple coloring)、分数染色(Fractional coloring)、适应点染色(Adaptive coloring)、对策染色(Game coloring)、DP-染色(DP-coloring),等等.另外，本文列出的一些结果也没有标出出处，读者可以从主要结果的被引处找到它们，在此谨向这些论文的作者们表示深深的歉意.