混沌驱动-响应系统形状渐近同步控制及其在保密通讯中的应用

黄运昌， 汤 晓， 王银河*

(1.广东工业大学 自动化学院， 广东 广州 510006； 2.广州亚俊氏电器有限公司， 广东 广州 510006)

0 引 言

混沌作为非线性系统的一种独特的动力学现象,在自然和工程实践中广泛存在[1-2].由于混沌现象的遍历性和伪随机性,因而它应用于许多工程实践中.近十几年来,混沌同步一直是研究非线性科学的热点课题之一.在混沌同步控制中,最典型的是完全同步[3-5],该同步保证驱动与响应混沌系统的状态变量随着时间的推移渐近趋于相同.针对这类同步,许多相应的驱动-响应控制方法被提出,例如,利用线性反馈控制实现驱动-响应混沌同步控制[3],考虑分数阶超混沌系统,通过滑模控制器实现两个系统的同步[4],针对一类不确定混沌系统,模糊自适应同步控制被提出[5].另外,对完全同步的概念进行延伸,又出现有广义同步[6]、投影同步[7]、滞后同步[8]、反同步[9]等.

值得注意的是,完全同步概念主要是基于混沌系统状态变量之间的距离关系,要求状态变量之间的距离渐近为零,其他类型的同步概念也直接与系统状态相关,并未涉及系统状态轨线的形状. 对于由微分方程确定的混沌系统,在给定的初始条件下,其状态解在其状态空间中呈现为一条空间轨迹曲线(吸引子),该曲线具有特定的形状,而且不同的混沌系统,其在状态空间中呈现的空间轨迹曲线的形状也不同.可见,系统状态轨线的形状也蕴含了系统运行的某些重要的信息,因而从混沌吸引子的形状出发讨论形状同步也具有一定的理论和实践意义,但是现有的相关文献鲜有涉及形状同步的研究.所谓“形状同步”,是指通过控制作用,使得驱动和响应混沌系统曲线的状态曲线趋于相同.文献[10]讨论了混沌系统的驱动-响应形状同步,并通过设计的控制器保证驱动-响应系统曲线的弧长和曲率完全相同,实现了形状完全同步.但是,该方法在混沌系统选取上具有一定的局限性,同时控制器也较为复杂,不易于推广.

基于微分几何的平面基本理论[11],二维平面曲线经过刚体变换,会发生相应的旋转、平移,但是其形状并不会发生改变.因此,对于二维平面中两条形状相同的曲线,一定存在某一刚体变换使得两条曲线重合.受此启发,只要保证驱动和响应系统曲线满足刚体变换关系,那么也可以实现形状同步.然而,如何通过结合刚体变换和同步控制使得驱动系统和响应系统曲线实现形状同步,目前这方面的研究仍然较少.

此外,混沌信号具有非周期性、连续宽带频谱、类噪声的特性以及异常复杂的运动轨迹和不可预测性,而且轨迹对初值非常敏感,使得混沌信号成为非常合适的保密通信的载体[12].混沌同步控制理论的发展,为混沌保密通讯技术的进一步发展奠定了理论基础.当前,同步保密通讯技术主要包括混沌遮掩技术、混沌键控技术和混沌参数调制技术[13].这些技术利用混沌同步控制,使发送端驱动和接收端响应系统状态变量距离满足完全相同或者一些特定关系,从而实现了保密信息复原.由于形状相同的吸引子之间的状态变量距离没有固定的关系,利用相同形状的混沌系统曲线进行传输,能够增加信号复原的难度,从而提高通讯保密的安全性.因此,基于形状同步的保密通讯具有实际的工程意义.

通过上述讨论,本文提出了混沌系统驱动-响应形状渐近同步的概念以及一种形状渐近同步控制器.此外,结合混沌掩盖技术,利用提出的形状同步控制方法,设计了一种形状同步保密通讯方案.

1 系统描述

一类混沌驱动系统[5]描述为

(1)

其中状态向量x(t)=[x1(t),x2(t)]∈R2,非线性函数f1(x(t),t)是一个光滑的时变向量函数,A1是常实数矩阵.

设响应系统描述为

(2)

其中状态向量y(t)=[y1(t),y2(t)]∈R2,非线性函数f2(y(t),t)是一个光滑的时变向量函数,A2是常实数矩阵,u(t)=[u1(t),u2(t)]T∈R2为控制输入.

注1：对于给定初始时刻t0和初始位置x(t0)=[x1(t0),x2(t0)]T,驱动系统具有满足这个初始条件的解φ(x(t0),t0),这个解在相平面内表现为光滑的平面曲线r1(t)=[x1(t),x2(t)]T,称为驱动系统曲线.同理,响应系统也表现为一条光滑的平面曲线r2(t)=[y1(t),y2(t)]T,称为响应系统曲线.

引理1.1[11]设c1(t)和c2(t)是R2中的两条平面曲线,如果c1(t)经过一个刚体运动后与c2(t)重合,那么称曲线c1(t)和曲线c2(t)形状完全相同,此时存在一个二维实数正交矩阵Q与实数向量p,满足Qc1(t)+p=c2(t).

将引理1.1中关于两条平面曲线形状完全相同的概念加以扩展,得到如下定义.

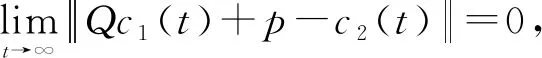
定义1.2考虑驱动系统(1)与响应系统(2),如果在控制输入u(t)作用下,从t0开始驱动系统曲线与响应系统曲线形状渐近相同,则称为形状渐近同步.

2 形状同步控制设计

控制目标：设计控制输入u(t)使驱动系统(1)与响应系统(2)在控制输入u(t)作用下形状渐近同步.

针对混沌驱动系统(1)和响应系统(2),定义形状同步误差如下：

z(t)=Qx(t)+p-y(t)

(4)

其中，Q为二维实数正交矩阵且QTQ=E(单位矩阵),p为实数向量.

其导数为

A2y(t)-f2(y(t),t)-u(t)

(5)

为了实现上述控制目标,对于响应系统的控制器可以设计如下:

u(t)=QA1QT(z(t)-p)+(QA1QT-A2)y(t)+

Qf1(x(t))-f2(y(t))+kz(t)

(6)

其中k为正可调参数.

定理2.1考虑混沌驱动系统(1)和响应系统(2),采用所设计的控制器(7),可保证驱动系统与响应系统达到形状渐近同步.

证明

首先,选取如下候选的Lyapunov函数：

(7)

其中,B为正定对称矩阵.

对其作时间的导数

(8)

将式(5)代入得到

以“两微一端”为代表的新媒体成为当下媒体发展的主流，越来越多的媒体借助微信、微博和客户端不断拓展发展平台。传统媒体的发展囿于电视传播，但是，移动设备的普及逐渐取代电视的功能，发挥更加灵活的作用。传统媒体只有与新媒体融合，借助手机客户端等推出简洁的信息传播方式，将图片、文字和视频等集中在较短的篇幅内传播，适应当下观众对效率和快节奏生活的要求，为传统媒体发展赢得更多的用户，创新信息传播的方式，扩展发展平台。

A2y(t)-f2(y(t),t)-u(t))

=zT(t)B(QA1QTQx(t)-QA1QTy(t)+

QA1QTy(t)-A2y(t)+Qf1(x(t),t)-

f2(y(t),t)-u(t))

(9)

由式(4)得：

A2)y(t)+Qf1(x(t))-f2(y(t))-u(t))

(10)

将控制器(6)代入式(10)中,得到

(11)

3 数值仿真

选用Duffing方程式[14]作为混沌驱动系统,其模型为如下方程,

(12)

其中

响应系统设计如下：

(13)

取

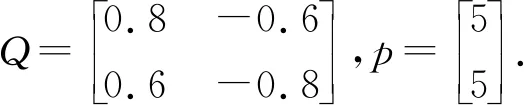
设计形状渐近同步控制器如下：

u(t)=QA1QT(z(t)-p)+(QA1QT-A2)y(t)+

Qf1(x(t))-f2(y(t))+kz(t).

选取k=5，通过Matlab软件仿真得到结果见图1～图2：

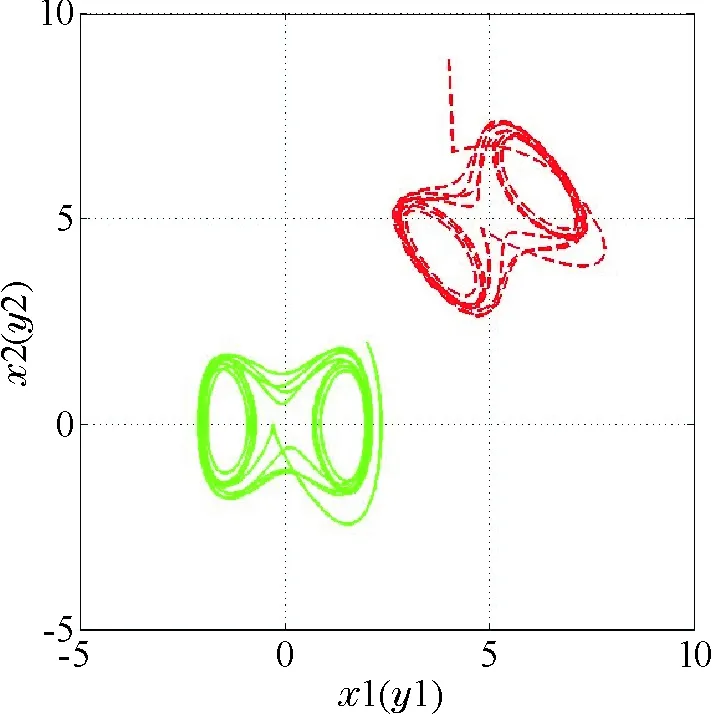
图1 相位图

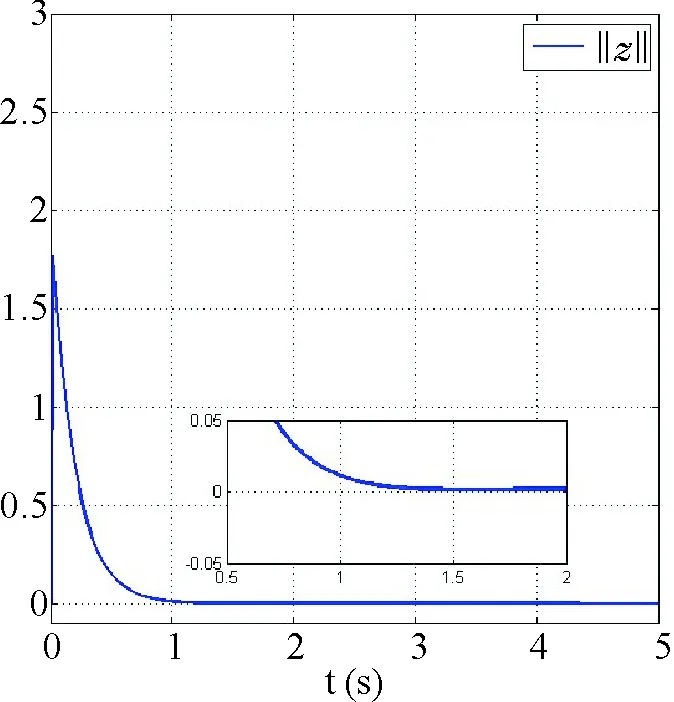
图2 形状同步误差

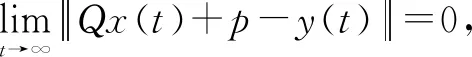
4 形状渐近同步在保密通信中的应用

上述仿真表明,由于形状同步对两个系统状态变量之间的距离没有固定的关系,因此，要使两者完全重合,需要通过平面的某一刚体变换才能实现.利用这一特点,形状渐近同步控制可以在保密通信中得到运用.即使截获传输的混沌系统信号,也仅能够得到加密信号和驱动信号的形状,具体的曲线位置并不能确定,无法破译传输信息,因此，提高了保密系统的安全性和灵活性.结合混沌掩盖技术,构建混沌形状同步保密通信系统见图3.

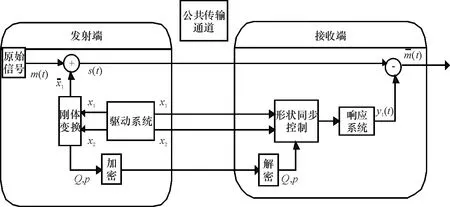
图3 保密通信系统

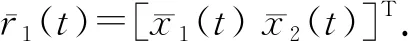
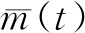
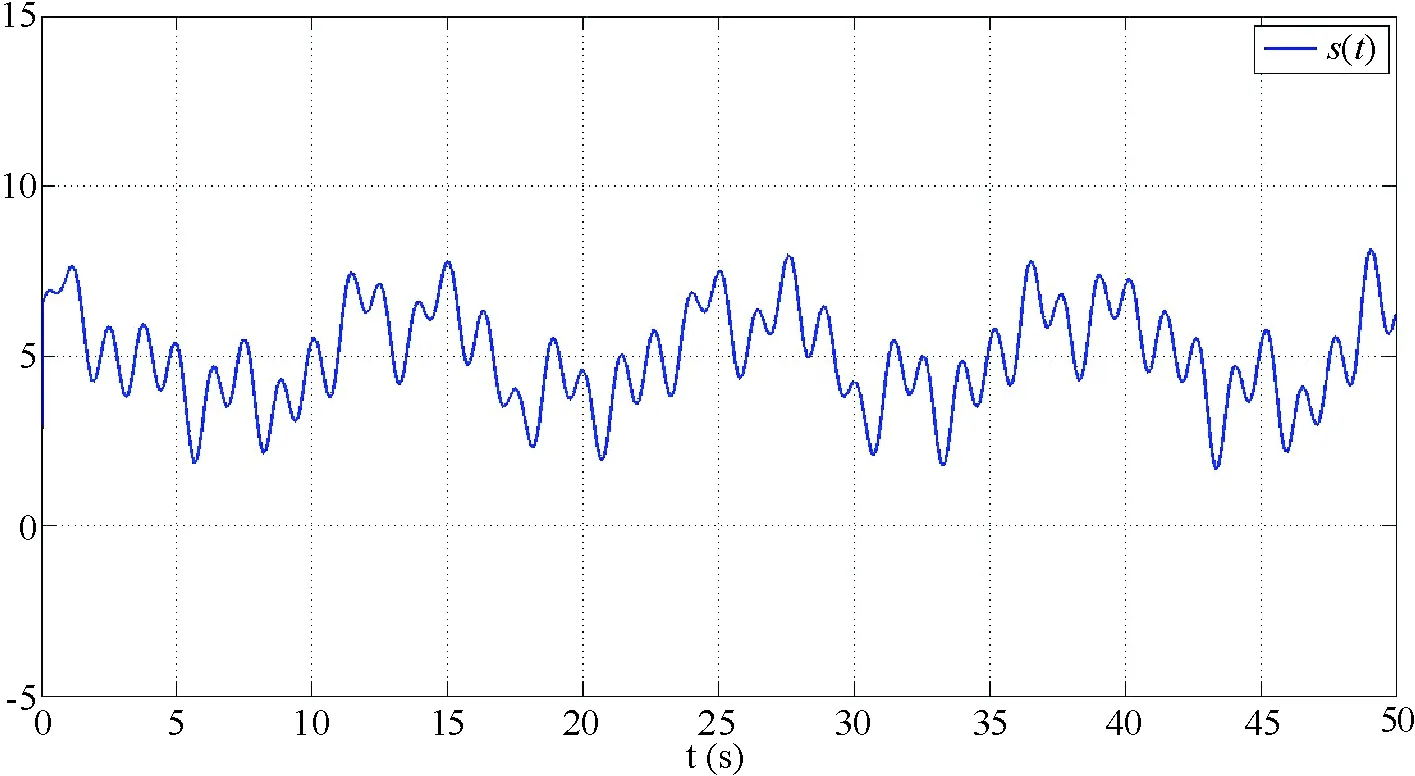
图4 公共传输信号

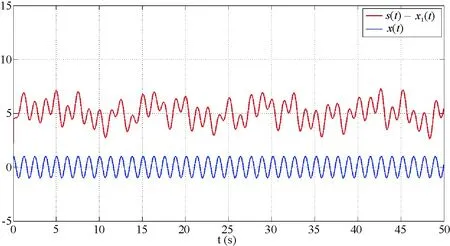
图5 传统方式复原信号与原始信号

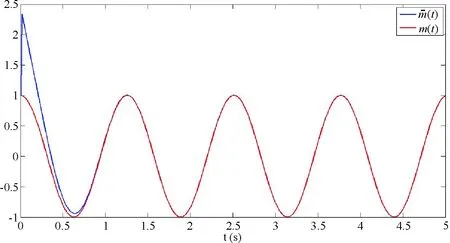
图6 响应输出信号与原始信号

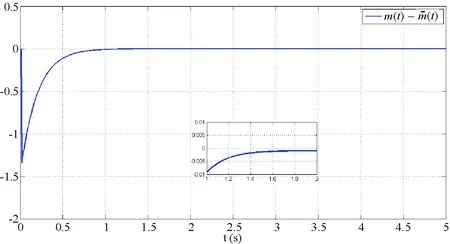
图7 复原误差

由上述理论分析和仿真结果可知，本文提出的形状渐近同步遮掩调制的混沌保密通信与传统的混沌保密通信方法相比有如下优点：

(1)传输信号是由驱动信号经过刚体变换后叠加原始信号形成的，即使信号被截获，两者之间的差值并非原始信号.因此,本方案具有较强的保密性.

(2)形状相同的曲线在二维平面中难以枚举，利用不同的刚体变换，可以提高密钥选择的灵活性，并增加保密性.

(3)渐近同步控制器可以调节参数使得响应时间加快，从而有效地减少通讯带来的干扰，尽可能地保证原始信号无失真的恢复.

5 结 论

本文针对一类二阶混沌系统,首先,基于微分几何基本理论,提出了驱动响应混沌系统曲线形状渐近同步的概念.形状渐近同步的提出拓宽和丰富了混沌同步理论.其次,通过设计形状同步控制器,保证了驱动系统和响应系统曲线形状渐近同步.根据Lyapunov 稳定性原理,对形状同步误差收敛进行了证明.同时,结合混沌掩盖的方法,设计了基于一类驱动响应混沌系统的形状同步混沌保密通信方案.最后,通过数值仿真进行验证.由于当前对于形状同步的研究较少,因此相应的理论仍需要深层次的完善和挖掘,同时基于形状同步的应用还有待进一步拓展.