基于神经网络的FRP抗震加固混凝土柱破坏模式预测

任 达， 黄宝全， 刘启华， 刘 坚

(广州大学 土木工程学院， 广东 广州 510006)

混凝土柱在水平地震荷载作用下，其破坏模式一般可分为弯曲破坏、剪切破坏及弯剪破坏三类.为满足“强剪弱弯”等延性设计要求，通常需要对抗剪能力或延性不足的柱进行加固，以避免其发生脆性剪切破坏或延性较差的弯剪破坏.已有研究表明[1-2]，高性能纤维增强复合材料(Fiber-Reinforced Polymer,FRP)横向缠绕混凝土柱不仅可以提高构件的承载力，且在配纤适量的情况下，能使破坏模式从剪切转变为弯曲破坏，改善延性，使其表现出良好的耗能能力.在抗震设防区，对于轴压比较高且无法通过调节截面尺寸改善延性的构件来说，这种方法尤其适用.应用此法的一个重要前提是，能对FRP加固混凝土柱的破坏模式做出合理预测.这既是抗震延性设计的基本要求，也符合一般设计理论步骤，对于把握机理、提高承载力计算精度亦有积极意义.然而，目前FRP加固混凝土柱的研究主要侧重于承载力方面，破坏模式方面大多限于对试验现象做定性描述，极少涉及模式判别以及预测.文献[3]提出的基于抗剪与抗弯承载力骨架曲线相对位置的破坏模式判别方法是一次有益探索，值得肯定.但该方法需要预知构件的承载力骨架曲线，且文中提及对于配纤量较少的柱，仍存在误判.因此，关于FRP加固混凝土柱破坏模式，目前尚缺乏简便、有效的判别，尤其是预测的方法.究其原因：首先，破坏机理尚不十分清楚，力学建模较为困难；其次，破坏模式的影响因素非常多，且相互之间并不完全独立，导致不少参数具有高度非线性特征，进一步增加了度量的难度.

人工神经网络(Artificial neural network)是模仿人脑信息处理机制提出的一种数学工具，对模糊、不确定信息具有很强的鲁棒性，可以充分逼近任意复杂的非线性关系，适用于理论建模有困难的场合.它在土木工程的应用涉及材性分析、承载力预测、损伤识别等诸多方面，在FRP加固混凝土结构方面，也已有一些实例[4-6].有鉴于此，本文利用人工神经网络建立模型，用于FRP加固混凝土柱在水平荷载作用下破坏模式的预测.

1 BP神经网络概述

人工神经网络是由大量的神经元有机联结而成的高度非线性系统.其中，多层前馈神经网络是目前应用最多的网络模型之一.作为其主要代表，BP网络被广泛用于各类建模问题.它是以误差反向传播算法(简称BP算法)为核心所建立的一类神经网络，即根据实际输出和目标输出之间的误差，采用梯度下降法逐层调整连接权及阈值，直到实际输出和目标输出之间的误差平方和小于某规定值，这时各层神经元连接权和阈值唯一确定了一个非线性映射关系即BP网络，其典型结构如图1所示.更详细的讨论参见文献[7].

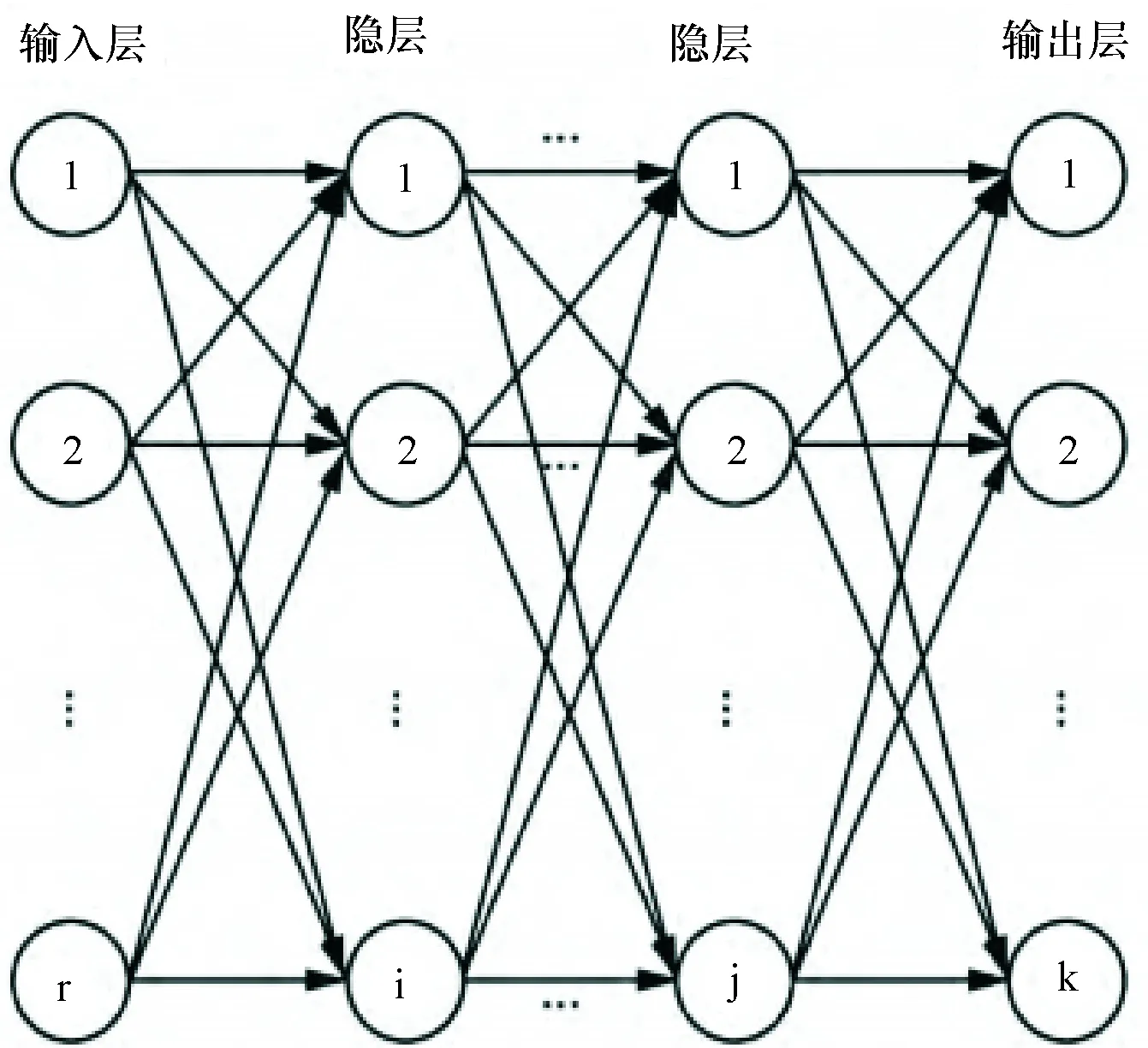
图1 BP神经网络结构

图2所示为单神经元结构.

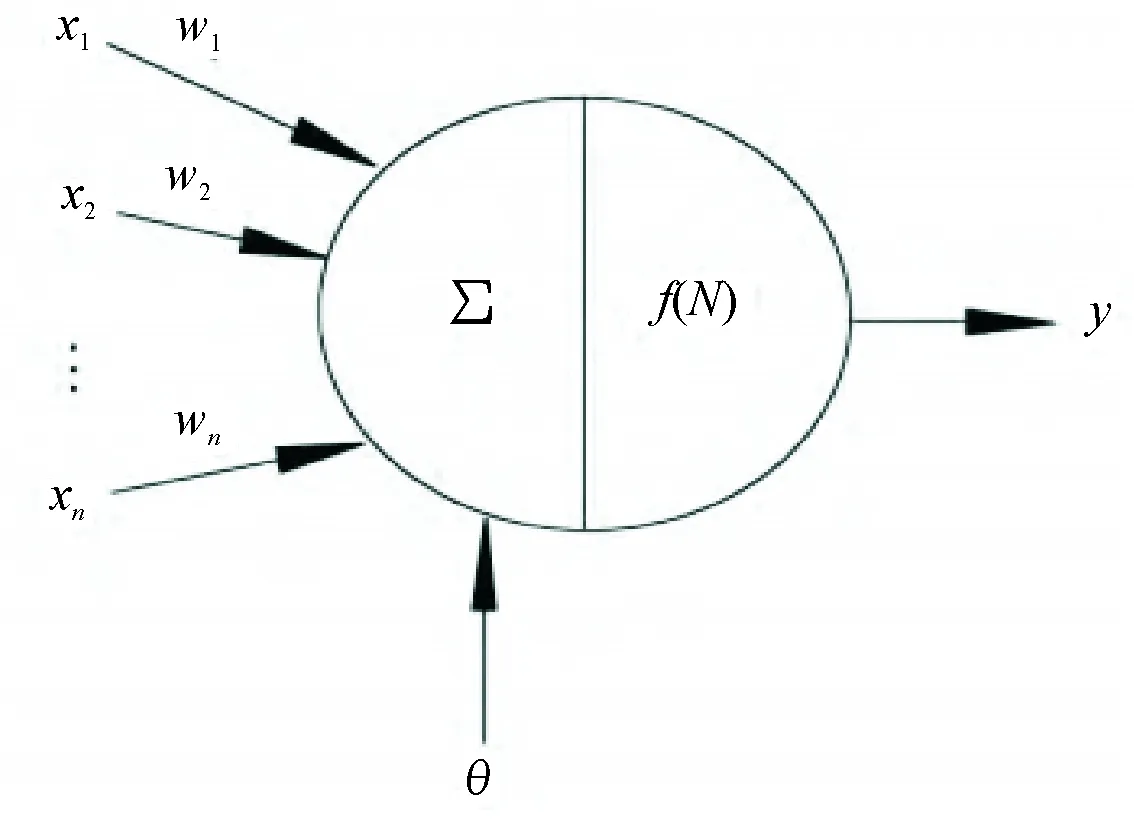
图2 单神经元结构

图2中x1、x2…xn为该神经元的输入信号；ω为各输入信号与该神经元之间的连接强度或系数，称为连接权值；θ为神经元的阈值，f(x)是传递或激活函数.网络中任一神经元输入和输出均为非线性映射，整个网络输入、输出向量之间为高度非线性函数关系.它通过具体算法学习训练，将样本数据中的关键信息进行提取训练，建立输入输出间的非线性映射关系，并根据其关系，由新的输入推算输出结果[8].

2 FRP抗震加固混凝土柱破坏模式BP网络预测模型

2.1 输入参量的选择

首先需对影响FRP抗震加固混凝土柱破坏模式的因素进行分析.由于以往针对FRP加固柱破坏模式的研究极少，数据资料较为缺乏，相对来说，对普通柱破坏模式的研究更多.为此，可在普通混凝土柱破坏模式影响因素(或称原柱参数)的基础上，增加考虑与加固相关的参数(或称加固参数).以下按原柱参数与加固参数分别对FRP加固混凝土柱破坏模式影响因素加以讨论.

与FRP加固柱的情况类似，专门针对普通混凝土柱破坏模式的研究也很少见，大多是在承载力研究基础上对其进行一些讨论[9-12].表1给出了已有文献关于普通混凝土柱破坏模式讨论中涉及的主要因素.原柱参数主要包括混凝土强度、柱几何尺寸及钢筋(纵筋、箍筋)配置相关参数等.其中，几何尺寸参数包括柱宽b、柱长h、柱高d等；剪跨比λ与轴压比n分别体现了水平剪力与竖向轴力的影响；纵筋屈服强度fy与箍筋屈服强度fyv体现了钢筋的力学性能；纵筋配筋率ρv与钢箍配箍率(包括体积配箍率ρvsv与面积配箍率ρasv)分别反映了纵筋与钢箍的配置量及钢箍在抗压与抗剪方面的加固效应.

表1 普通混凝土柱破坏模式影响因素或原柱参数的考虑

注：“√”：考虑了该参量的影响；“-”：该项未考虑.

加固参数主要考虑增加纤维材料性能(种类)、配置量及其配置(加固)方式等.其中，纤维材性参数主要以抗拉强度ff、弹性模量Ef等反映；纤维配置量主要以FRP厚度tf、FRP宽度wf、FRP层数nf、FRP中心距sf及配纤率(包括体积配纤率ρvf与面积配纤率ρaf)等反映其影响.此外，由于极限承载力Fu与破坏模式之间有密切关联，因而也被选作输入参量.这里将文献[3]及本文中所考虑的加固参数列于表2.

表2 加固参数的考虑

注：1.“√”：考虑了该参量的影响；“-”：该项未考虑.2.为抗剪FRP有效应变.

需要指出，在原柱与加固参数中，分别包括了两种不同的钢箍配箍率与配纤率，其原因在于：体积配箍率或配纤率，主要反映了钢箍或纤维通过约束混凝土的横向膨胀、抑制纵筋屈曲等对构件受压、受弯性能乃至破坏模式的作用；而面积配箍率或配纤率，反映的则是横向钢箍或纤维对构件受剪性能乃至破坏模式的影响.不同的配箍或配纤量计量方法实际体现了同一种钢箍或纤维配置方式的不同加强或加固效应.

综合上述原柱和加固参数的讨论，网络模型所选取的输入参量见图3.

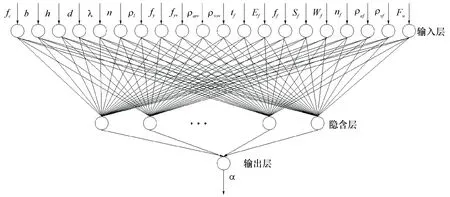
图3 FRP抗震加固混凝土柱破坏模式BP网络预测模型拓扑图

2.2 隐层数与节点数的确定

隐含层数目以及各隐层包含的节点数决定了一个网络模型的基本架构.神经网络理论研究表明，一个3层BP网络具有逼近任何复杂非线性函数的能力.因此，本文拟采用单隐层的BP网络构建FRP加固混凝土柱破坏模式预测模型.隐层数确定后，需要进一步确定隐层中所含的节点数量.其数目过大会造成网络结构庞大，使得训练时间或成本大大增加；数量太少则可能引起曲线模拟效率降低、收敛困难，甚至无法达到训练的误差精度要求.为此，文献[13]提出了一个用于BP网络训练、效率较高的隐含层节点数计算公式，即

(1)

其中，n1为隐含层单元数，n为输入单元数，m为输出单元数，a为[1，10]之间的常数.根据式(1)计算得到隐含层节点数n1取值范围为[4～14]，经过多次试算，当隐含层节点数量为7时，可获得最优训练效果.图3所示即FRP加固混凝土柱破坏模式BP网络预测模型拓扑结构图.由图3可知，网络模型结构由1个输入层(含20个节点)、1个隐含层(含7个节点)和1个输出层(含1个节点，即破坏模式)组成，简记为20-7-1.

2.3 输入数据的归一化

以往经验表明，用于网络训练的输入参量种类不一，所采用的量纲各异，因而最大和最小数据之间可能相差若干数量级，在网络训练过程中，容易产生较大的舍入误差，使得训练效果大打折扣.为了避免出现上述情况，常常需要对输入数据进行“归一化”处理，以保证所有输入数据均处于同一个量级范围内，即对原始数据做如下转换，

(2)

式中,x0为原始数据，x1为归一化后的数据，xmin、xmax分别为原始数据中的最大值与最小值，转换后所有数据位于0.1～0.9之间，用此方法以改善BP网络收敛速度.

破坏模式一般是在试验观测基础上区别不同破坏特征来界定的，并非数据类型的参量，故需要进行量化，方可用于网络训练及输出.为了定量的描述破坏模式，现引入破坏模式量化指标α，取值如下：剪切破坏α=-1，弯剪破坏α=0，弯曲破坏α=1.采用式(2)对输入数据进行预处理后，得到归一化指标αs.通常，网络预测值恰好等于归一化指标αs的情形是极少的，它们大多介于归一化指标界限值之间，因而需要对网络输出值所代表的破坏模式做出界定.三类破坏模式的归一化指标αs之间相差均为0.4,以相邻两者的中间值0.3与0.7为界，即确定了三类破坏模式各自对应的BP网络预测值有效范围(表3).

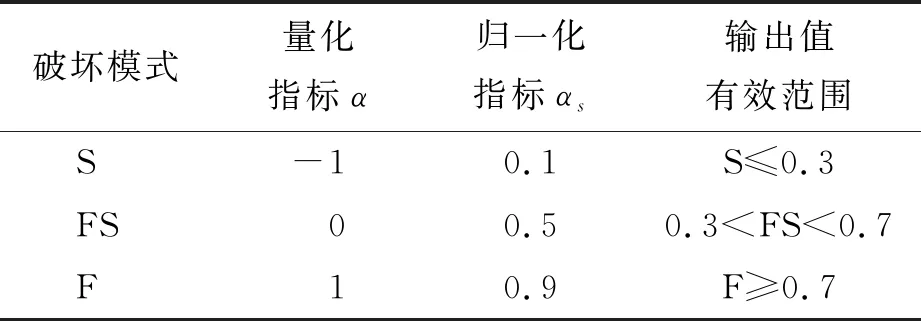
表3 破坏模式的量化

注：S代表剪切破坏，FS代表弯剪破坏，F代表弯曲破坏，下同.

2.4 网络学习与训练

训练样本的选取主要考虑两个方面：训练样本数量与样本入选条件.样本的选取最关键的并不在于样本数量，而是所选的样本要有代表性，能够提高模型预测精度.换言之，同样数量的样本，代表的情况越多，包含的信息范围越广，BP网络训练精度也就越高.因此，为保证所选样本的信息量大，在纤维加固柱数据中，所有输入参量变化区间上、下限值的样本优先选取，以保证学习样本集覆盖所列的参数变化范围.表4列出了从国内外文献中搜集到的71根FRP抗震加固混凝土柱试验数据，其主要加固形式为绕柱横向粘贴，并根据上述原则，从中选取了36根试件用于网络训练，其余试件用于网络预测.

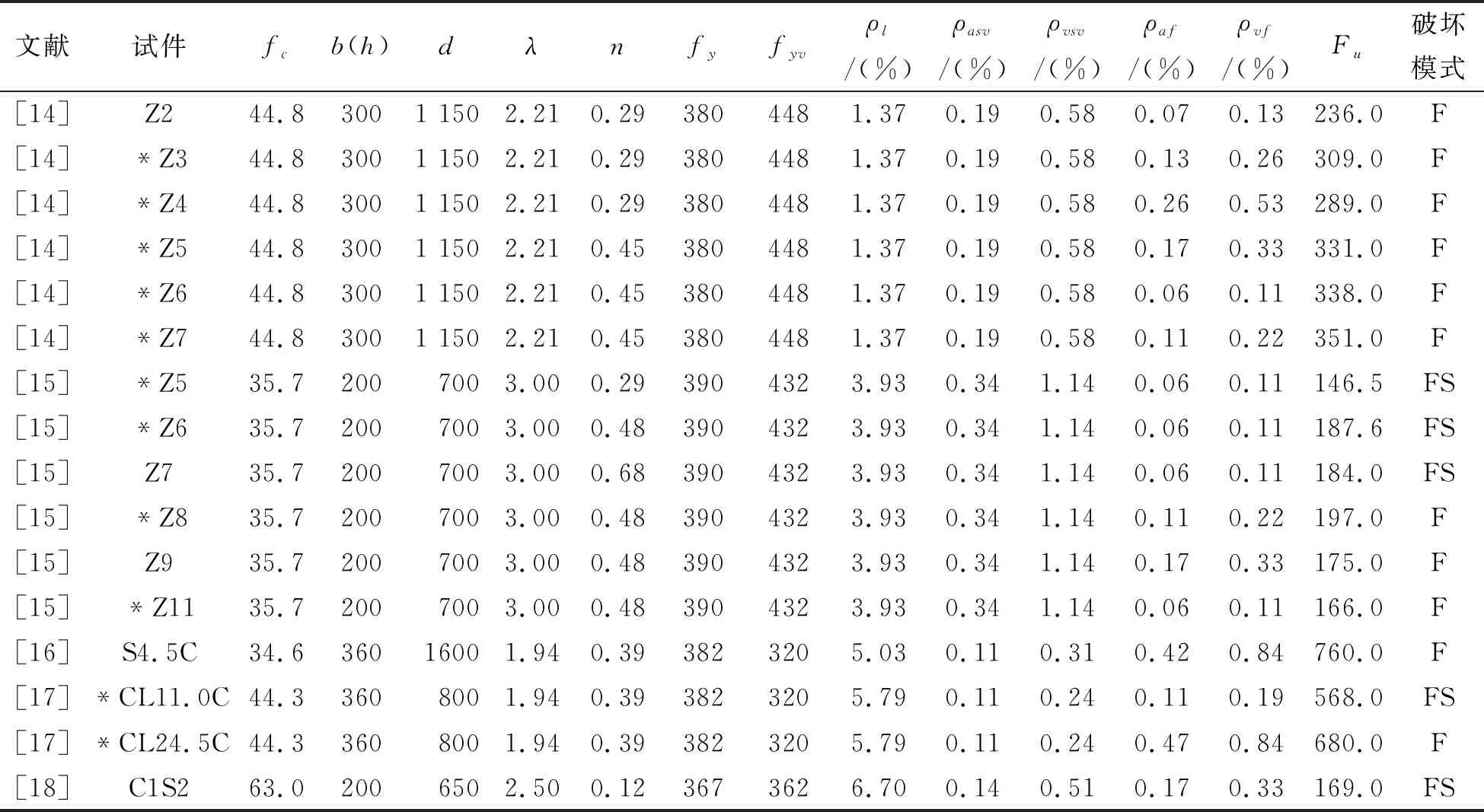
表4 各有关文献FRP抗震加固混凝土柱主要试验数据

(续表4)

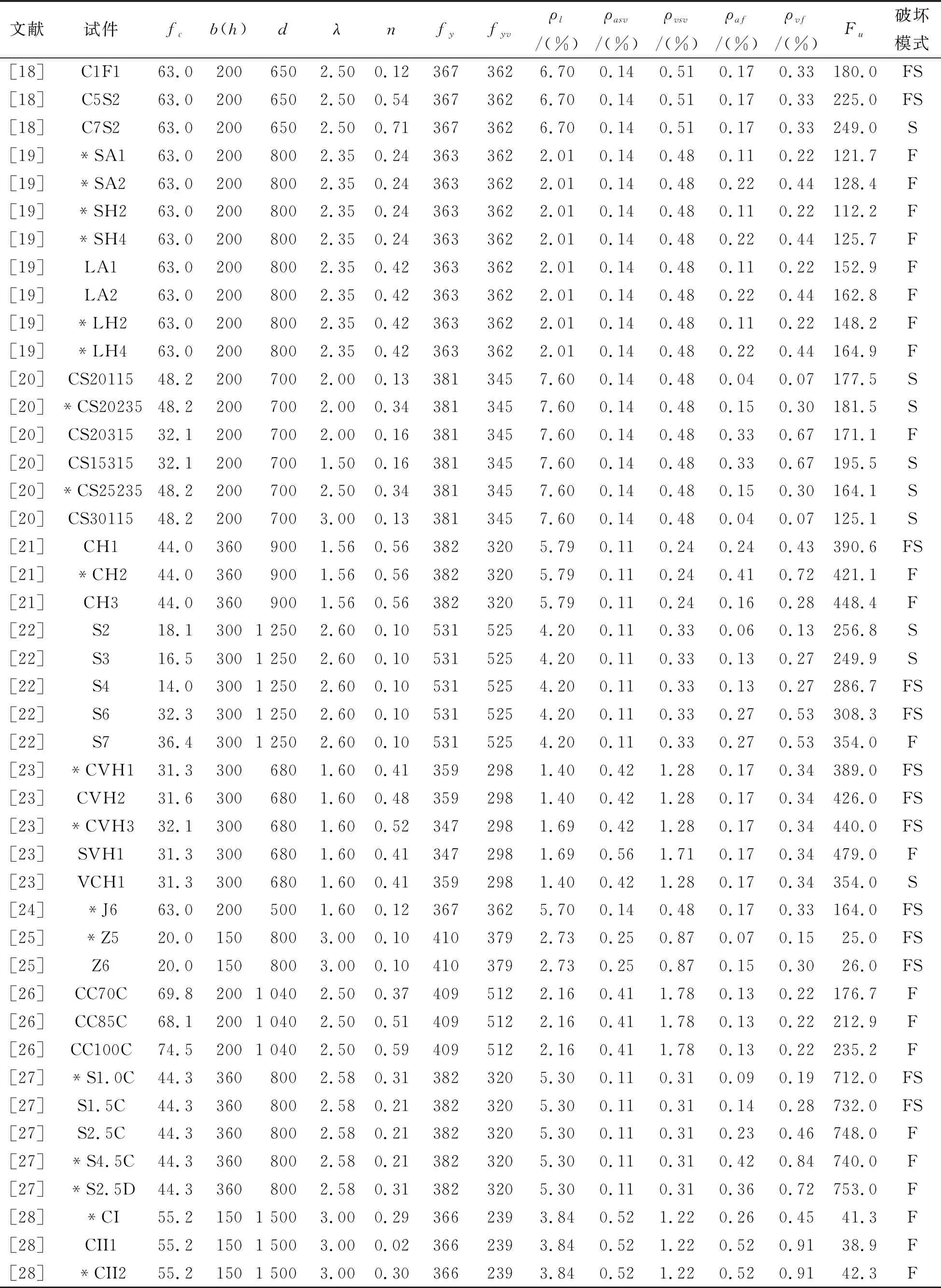
文献试件fcb(h)dλnfyfyvρl/(%)ρasv/(%)ρvsv/(%)ρaf/(%)ρvf/(%)Fu破坏模式[18]C1F163.02006502.500.123673626.70 0.140.51 0.17 0.33 180.0FS[18]C5S263.02006502.500.543673626.70 0.140.51 0.17 0.33 225.0FS[18]C7S263.02006502.500.713673626.70 0.140.51 0.17 0.33 249.0S[19]*SA163.02008002.350.243633622.01 0.140.48 0.11 0.22 121.7F[19]*SA263.02008002.350.243633622.01 0.140.48 0.22 0.44 128.4F[19]*SH263.02008002.350.243633622.01 0.140.48 0.11 0.22 112.2F[19]*SH463.02008002.350.243633622.01 0.140.48 0.22 0.44 125.7F[19]LA163.02008002.350.423633622.01 0.140.48 0.11 0.22 152.9F[19]LA263.02008002.350.423633622.01 0.140.48 0.22 0.44 162.8F[19]*LH263.02008002.350.423633622.01 0.140.48 0.11 0.22 148.2F[19]*LH463.02008002.350.423633622.01 0.140.48 0.22 0.44 164.9F[20]CS2011548.22007002.000.133813457.60 0.140.48 0.04 0.07 177.5S[20]*CS2023548.22007002.000.343813457.60 0.140.48 0.15 0.30 181.5S[20]CS2031532.12007002.000.163813457.60 0.140.48 0.33 0.67 171.1F[20]CS1531532.12007001.500.163813457.60 0.140.48 0.33 0.67 195.5S[20]*CS2523548.22007002.500.343813457.60 0.140.48 0.15 0.30 164.1S[20]CS3011548.22007003.000.133813457.60 0.140.48 0.04 0.07 125.1S[21]CH144.03609001.56 0.563823205.79 0.110.24 0.24 0.43 390.6FS[21]*CH244.03609001.56 0.563823205.79 0.110.24 0.41 0.72 421.1F[21]CH344.03609001.56 0.563823205.79 0.110.24 0.16 0.28 448.4F[22]S218.1 3001 2502.600.105315254.20 0.110.33 0.06 0.13 256.8S[22]S316.53001 2502.600.105315254.20 0.110.33 0.13 0.27 249.9S[22]S414.03001 2502.600.105315254.20 0.110.33 0.13 0.27 286.7FS[22]S632.33001 2502.600.105315254.20 0.110.33 0.27 0.53 308.3FS[22]S736.43001 2502.600.105315254.20 0.110.33 0.27 0.53 354.0F[23]*CVH131.33006801.600.413592981.40 0.421.28 0.17 0.34 389.0FS[23]CVH231.63006801.600.483592981.40 0.421.28 0.17 0.34 426.0FS[23]*CVH332.13006801.600.523472981.69 0.421.28 0.17 0.34 440.0FS[23]SVH131.33006801.600.413472981.69 0.561.71 0.17 0.34 479.0F[23]VCH131.33006801.600.413592981.40 0.421.28 0.17 0.34 354.0S[24]*J663.02005001.600.123673625.70 0.140.48 0.17 0.33 164.0FS[25]*Z520.01508003.000.104103792.73 0.250.87 0.07 0.15 25.0FS[25]Z620.01508003.000.104103792.73 0.250.87 0.15 0.30 26.0FS[26]CC70C 69.82001 0402.50 0.374095122.16 0.411.78 0.13 0.22 176.7F[26]CC85C 68.12001 0402.50 0.514095122.16 0.411.78 0.13 0.22 212.9F[26]CC100C74.52001 0402.50 0.594095122.16 0.411.78 0.13 0.22 235.2F[27]*S1.0C44.33608002.580.313823205.30 0.110.31 0.09 0.19 712.0FS[27]S1.5C44.33608002.580.213823205.30 0.110.31 0.14 0.28 732.0FS[27]S2.5C44.33608002.580.213823205.30 0.110.31 0.23 0.46 748.0F[27]*S4.5C44.33608002.580.213823205.30 0.110.31 0.42 0.84 740.0F[27]*S2.5D44.33608002.580.313823205.30 0.110.31 0.36 0.72 753.0F[28]*CI55.21501 5003.000.293662393.84 0.521.22 0.26 0.45 41.3F[28]CII155.21501 5003.000.023662393.84 0.521.22 0.52 0.91 38.9F[28]*CII255.21501 5003.000.303662393.84 0.521.22 0.52 0.91 42.3F

(续表4)

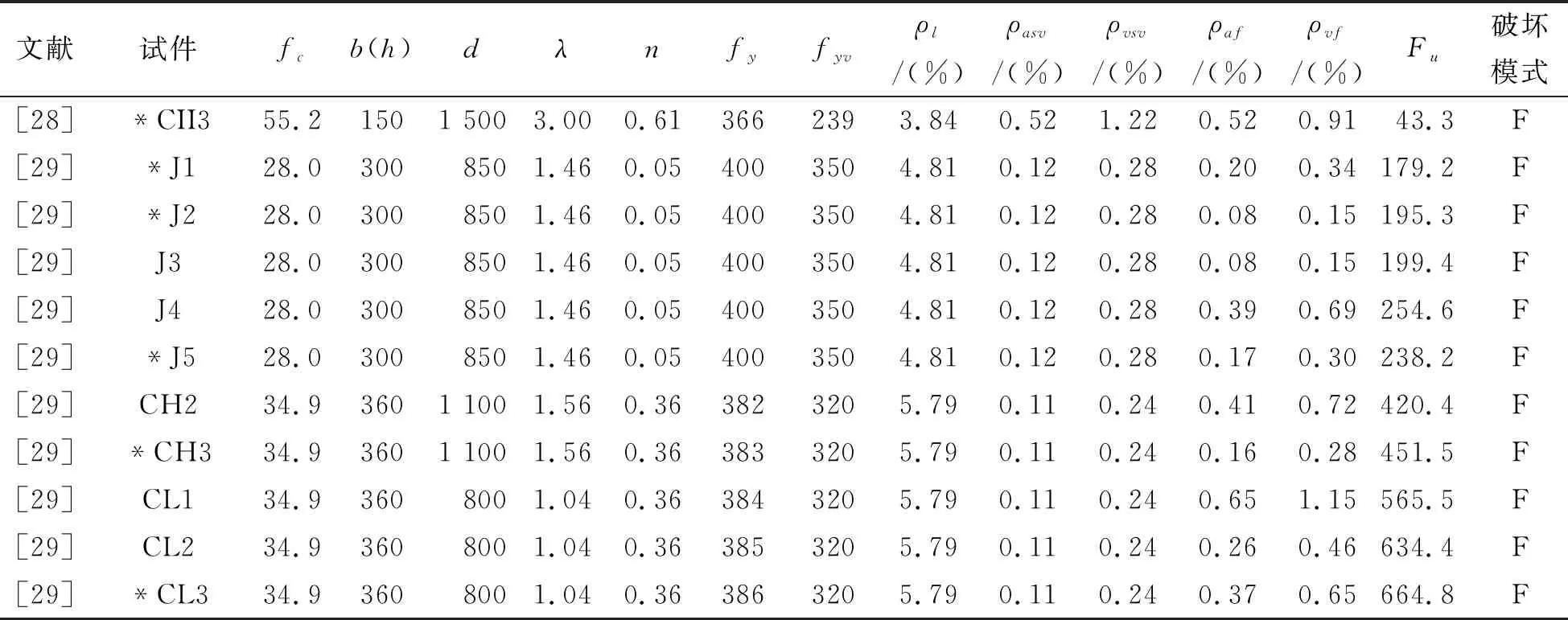
文献试件fcb(h)dλnfyfyvρl/(%)ρasv/(%)ρvsv/(%)ρaf/(%)ρvf/(%)Fu破坏模式[28]*CII355.21501 5003.000.613662393.84 0.521.22 0.52 0.91 43.3F[29]*J128.03008501.46 0.054003504.81 0.120.28 0.20 0.34 179.2F[29]*J228.03008501.46 0.054003504.81 0.120.28 0.08 0.15 195.3F[29]J328.03008501.46 0.054003504.81 0.120.28 0.08 0.15 199.4F[29]J428.03008501.46 0.054003504.81 0.120.28 0.39 0.69 254.6F[29]*J528.03008501.46 0.054003504.81 0.120.28 0.17 0.30 238.2F[29]CH234.93601 1001.56 0.363823205.79 0.110.24 0.41 0.72 420.4F[29]*CH334.93601 1001.56 0.363833205.79 0.110.24 0.16 0.28 451.5F[29]CL134.93608001.04 0.363843205.79 0.110.24 0.65 1.15 565.5F[29]CL234.93608001.04 0.363853205.79 0.110.24 0.26 0.46 634.4F[29]*CL334.93608001.04 0.363863205.79 0.110.24 0.37 0.65 664.8F

注：1.表中单位制：长度为mm，材料强度为MPa，荷载为kN；2.混凝土强度均取立方体抗压强度，圆柱体抗压强度除以0.79系数换算为立方体强度值；圆柱试件按《混凝土结构设计规范GB50010-2010》[30]中规定等效为方柱，即方柱边长=1.76×圆柱半径；3.带*试验数据为预测样本，其余为训练样本；4.所列试件均属于FRP加固完好混凝土柱的情况，并以CFRP加固试件为主，仅含少数AFRP(芳纶纤维)、BFRP(玻璃纤维)、DFRP(高分子聚乙烯纤维)加固试件.

具体程序采用MATLAB语言编制，传递函数采用网络工具箱的tansig(输入层、隐层)、logsig函数(输出层)，训练函数为适用批量数据处理的traingdx，该函数收敛性较差，但预测误差小，由于其可能存在收敛困难的情况，设定训练终止次数为5 000，同时目标误差定为0.01，动量系数取为0.9，学习率取0.05.训练过程见图4，经907次后，BP网络收敛于目标误差(图中水平虚线)，训练结束.

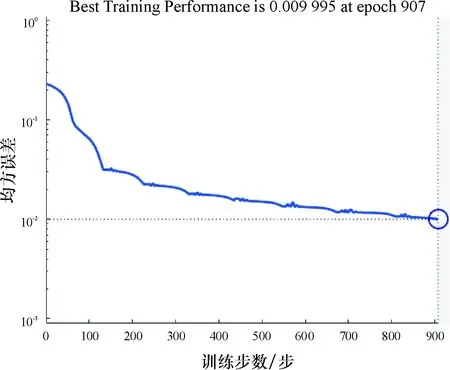
图4 BP神经网络训练过程

3 基于BP网络模型的破坏模式预测

首先，利用训练好的BP网络预测模型，对训练数据之外的35根柱(表4中带“*”标识的数据)的破坏模式进行了预测.然后，计算出网络预测输出值与试件实测破坏模式对应的归一化指标之差，用以反映网络模型预测的误差.最后，以散点图的形式将预测误差绘制成图5.结果表明，预测结果与试验观测的误差绝大部分落在±0.2区间，说明所建BP网络模型对于FRP抗震加固混凝土柱破坏模式的预测效果较佳.

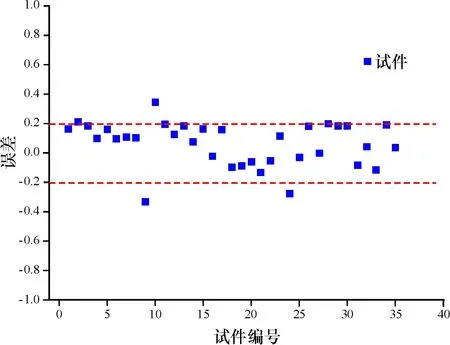
图5 预测误差

表5将破坏模式网络模型预测值与试验观测结果做了对比.可见，BP网络模型预测值与试验观测结果的符合率超过了90%.本文建立的BP网络模型能较好地预测FRP加固混凝土柱在水平荷载下的破坏模式.

表5 网络预测与试验观测结果对比

Table 5 Comparison between the experimental observations and predictions by the BP neural-network model

判别方法FFSS符合率/%试验观测2582100网络预测257391

4 结 论

采用FRP对混凝土柱进行横向缠绕加固是改善其抗震性能的一种有效手段.对于抗震加固混凝土柱的破坏模式，尚无有效预测方法.本文在全面分析影响FRP加固柱破坏模式主要因素的基础上，依据人工神经网络理论，建立了FRP抗震加固混凝土柱的破坏模式BP网络预测模型，并对35个FRP抗震加固试件的破坏模式做了预测，得到如下结论：

(1)对于FRP抗震加固混凝土柱的破坏模式，本文所建立的BP网络模型预测值与试验观测结果的符合率超过了90%，可用于FRP抗震加固混凝土柱的破坏模式预测；

(2)训练试验数据还不够多，数据样本结构尚不够合理，参数覆盖范围仍不够广，对于取值范围外的试件预测结果仍需验证.主要体现为试件截面均为方形或圆形，缺少矩形柱，且均为完好柱加固，无预持载柱加固情形.此外，碳纤维加固试件多，其他类型纤维加固试件较少；

(3)网络模型结构有待优化改进.由于神经网络理论自身仍不完善，需要对网络模型中隐含层数目、各隐层节点数及有关模型参数进行优化，以进一步提高模型预测效率和精度.