图谱确定问题综述

王 卫

(西安交通大学 数学与统计学院, 陕西西安 710049)

图谱蕴含着图的大量组合结构信息，一直以来是图论研究中强有力的工具. “哪些图是谱确定的？”是图谱理论中一个长期未解决的基本问题，该问题最早可追溯到两位化学家Günthard和Primas于1956年发表的文章[1]，他们将图谱理论与化学中Hückel的分子轨道理论联系在了一起.谱确定问题的另一个主要研究动机源于图论中的一个最基本的问题——图同构问题，即给定两个图，判定它们是否同构.由于在计算复杂性理论中占有独特地位,该问题一直以来备受人们关注.最近Babai[2]取得了突破性进展，给出了图同构问题的拟多项式时间算法，为三十多年来最好的结果，但该问题到底属于 P 还是NP-完全问题仍悬而未决.

图谱确定问题还与其他领域的一些问题有紧密联系.1966年，Kac[3]提出了一个著名问题：“我们能听鼓辨出其形状吗？”Fisher[4]考虑了这个问题,他将鼓的形状用一个图来模拟,而鼓的声音则由图谱刻划.这样Kac的问题本质上就是图谱确定问题.这一问题可进一步推广至黎曼几何中,见文献[5-8].

van Dam等[9-10]分别于2003年和2009年发表了关于上述问题的综述文章.现在十余年过去了，这一领域也取得了一些新的进展，本文主要对近十年来这一领域的一些新成果加以整理回顾，并列出一些仍亟待解决的问题，希望引发进一步的研究.

现在引入一些概念和符号.给定一个简单图G,令M=M(G)为与图G关联的矩阵，譬如M可以是图的邻接矩阵A、拉普拉斯矩阵L、无符号拉普拉斯矩阵Q,距离矩阵D等.矩阵M的特征值全体(包括重述)称为图的M-谱，记为SpecM(G).本文主要考虑图的邻接谱、(无符号)拉普拉斯谱、距离谱，以及广义谱.两个图G,H称为M-同谱，如果它们关于M-矩阵的谱相同，即SpecM(G)=SpecM(H).一个图G称为由其M-谱确定(determined by itsM-spectrum,简称DMS)， 如果对任意图H, 有SpecM(G)=SpecM(H)蕴含H同构于G.若一个图G是M-谱确定的，则称之为DMS-图.

本文简要阐述了关于图的邻接谱确定的一些结果，给出了(无符号)拉普拉斯谱确定性，详细介绍了图谱距离谱确定性，讨论了图的广义谱确定性的一些结果.

1 图的邻接谱确定性

本节考虑图关于邻接矩阵A的谱确定性.现有的DAS-图大都具有以下特点：该图或其补图的谱半径很小.通过谱半径的估计确定同谱图的度序列，然后将可能的同谱不同构的图类加以排除.早期人们已经得到了一类特殊树，譬如Zn,T-型树T(a,b,c)，以及一般的星型树的谱刻画.近年来又有更多的特殊图类被证明是DAS的.

一个风筝图(Kite graph)是由一个p个顶点的完全图Kp的一个顶点连接一个q个顶点的悬挂路得到的图，Topcu等[11]证明了下述定理:

定理1.1[11]所有风筝图可由其邻接谱确定.

一个菠萝图，记为Kpq(p≥3,q≥1)，是由一个p个顶点的完全图通过在一个顶点加q条悬挂边得到的图.Topcu等[12-13]证明了以下结果：

定理1.2 如果限定在连通图类中，Kpq(p≥3,q≥1)可由其邻接谱确定.反之可以确定所有的p，q使得存在一个不连通图与KpqA-同谱且不同构.

一个哑铃图，记为Da,b,c，是由两个不交圈Ca和Cb通过一条c+3个顶点的路Pc+3分别连接两个端点得到的图.Wang等[14]得到了下述结果：

定理1.3 不含4-圈C4的哑铃图Da,b,c可由其邻接谱确定.

一个图称为友谊图(Friendship graph)，记为Fk，是k个边不相交的三角形将其中每个三角形恰选一个顶点粘合在一起得到的图(风车图).Wang等[15]猜测友谊图是DAS的.Das[16]声称给出了一个证明.Abdollahi等[17]指出证明中的一个错误，并证明了一些特殊情形.Cioabă等[18]通过分析仅有两个特征值不等于±1的图，得到了友谊图谱确定性的下述完整结果：

定理1.4 友谊图Fk当k≠16时是DAS的.

Ramezani等[19]证明了下述结果：

定理1.5 一个奇圈与K2的笛卡尔积C2t+1×K2是DAS的.

Camara等[20]研究了何时一个完全图删去一些边得到的图是DAS的.他们提出以下猜想：

猜想1.1 令Pl为一个完全图Kn的子图，Kn删去Pl后得到的图记为Kn〗Pl，则Kn〗Pl对于所有1≤l≤n是DAS的.

上述猜想当l=n时成立，这是Doob等[21]中的主要结果.对该猜想的一些特殊情形，有以下定理：

定理1.6 上述猜想当l≤5时成立.

定理1.7[22]上述猜想当l=7,8,9时成立.

需要指出的是，近年来Koolen等[23-24]发展了Hofmman等关于线图刻画的深刻理论，得到了最小特征值大于-3的图的一些刻画.基于此，他们能够证明，譬如两个完全图Kt的笛卡尔乘积构成的t×t-格子图的2-团扩张(即将每个顶点换成K2，新的顶点相邻当且仅当原来的顶点相邻)是DAS的，即：

定理1.8[25]当t足够大时，(t+1) × (t+1)-格子图的2-团扩张图是DAS的.

2 图的(无符号)拉普拉斯谱确定性

给定一个图G，其邻接矩阵为A，度对角矩阵为D，则拉普拉斯矩阵定义为L=D-A；无符号拉普拉斯矩阵定义为Q=D+A.图的拉普拉斯谱可确定图的连通分支数目及生成数数目；无符号拉普拉斯谱可确定一个图二部图的分支数目.这些在研究图谱确定问题中都有重要应用.

一个有k个花瓣的k-玫瑰图，记为G=R(m1,m2,…,mk)，是由恰好有一个公共顶点的m个圈Cm1,Cm2,…,Cmk构成的图，若k=2， 则该图称为一个∞-图.Wang等[26]，Liu等[27]证明了以下结果：

定理2.1一个3-玫瑰图可由无符号拉普拉斯谱确定；一个3-玫瑰图则可由拉普拉斯谱确定.

定理2.2[28]一个没有三角形的∞-图是DLS的;∞-图是DLS的.

关于玫瑰图，He等[29]证明了下述一般性结果：

定理2.3 除了R(3,4)和R(3,5)外，所有k-玫瑰图是DLS.

一个蝴蝶图是一个玫瑰图在其中心再添加一些悬挂的路得到的图.Wen等[30]猜测：所有蝴蝶图是DLS的，同时也是DQS的.Liu等[31]证实了该猜想是正确的：

定理2.4 所有蝴蝶图既是DLS的，同时也是DQS的.

一个星型树，记为T=T(l1,l2,…,lk)，是一个恰有一个顶点度大于2的树，令v为其最大度，则T(l1,l2,…,lk)-v=Pl1∪Pl2∪…Plk.早期Lepovic 和Gutman证明了没有两个星型树A-同谱；Wang和Xu得到了当k=3时所有DAS的T-型树，并证明了所有T-型树是DLS的；Omidi等证明了所有星型树是DLS的；Omidi[32]得到了所有DQS的T-型树；Omidi等[33]证明了最大度为4的星型树是DQS的，Bu等[34]证明了一个最大度大于4的星型树是DQS的，从而有以下结果：

定理2.5 最大度大于3的星型树是DQS.

Zhou等[35]考虑了一类乘积图的DLS性.令G,H是两个顶点不交的图，G,H的乘积，记为G×H，是一个由G∪H通过连接G的每个顶点与H的每个顶点得到的图.譬如Cn×K1是一个轮图.

定理2.6[35]令G是一个不连通的DLS图，则G×Km是DLS的.

定理2.7[35]令G是一个至少有5个顶点的DLS树，或是一个至少有6个顶点的单圈DLS图，则G×Km是DLS的.

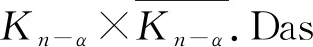
定理2.8 完全分裂图CS(n,α)(1≤α≤n-1)是DQS的；完全分裂图CS(n,α)(1≤α≤n-1,α≠3) 是DLS的.

关于拉普拉斯谱有以下问题：

问题：一个树的度序列可否由拉普拉斯谱确定？

3 图的距离谱确定性

给定一个连通图G，其距离矩阵D(G)=(dij)n×n，其中dij为顶点i与j之间的距离.令ti=∑d(vi,vj)为顶点vi到其余顶点的距离之和.令T(G)=diag(t1,t2,…,tn)，则图G的距离拉普拉斯矩阵定义为L(G)=T(G)-D(G)，距离无符号拉普拉斯矩阵定义为Q(G)=T(G)+D(G).图的距离各种谱及距离谱确定性近年来得到了广泛关注，见文献[37].

Lin等[38]刻画了最小距离特征值λn(D)=-2且重数为n-k的图——这样的图为完全k-部图(2≤k≤n-1).他们证明了完全二部图及完全split图是距离谱确定的，并提出了以下猜想：

猜想3.1 令G=Kn1,n2,…,nk为一个完全k-部图,则G可由其距离谱确定.

Jin等[39]证明了上述猜想成立:

定理3.1 完全k-部图可由其距离谱确定.

一个双星树，记为S(a,b)，是由两个相交的星型树K1,a和K1,b通过添加一条边连接其中心得到的图.Xue等[40]证明了下述结果：

定理3.2 一个双星树S(a,b)是距离谱确定的.

Xue等[41]，Lin等[42]考虑了圈与道路以及其补图的距离谱确定性.

定理3.3 一个圈Cn和道路Pn的补图分别可由距离谱，距离(无符号)-拉普拉斯谱确定.

一个d-超立方体可定义如下：其顶点集为所有长度为d的(0，1)——向量，两个向量相邻当且仅当它们恰有一个分量不相同.Koolen等[43]证明了下述定理：

定理3.4d-超立方体可由其距离谱确定.

Aouchiche等[46]利用计算机进行数值研究了10个顶点以内图的关于距离谱，(无符号)拉普拉斯距离谱同谱的所有图，确定了其中的谱确定图.

关于图的距离谱有以下问题[43]：

问题1： 图的距离谱是否可以决定该图是否是二部图？

问题2：一个距离正则图和一个非距离正则图是否能够有相同距离谱？

问题3：Hamming图H(d,q)当q≠4时是否是距离谱确定的？

4 图的广义谱确定性

图的广义谱确定最早是由Wang等[47]研究的,他们给出了一般随机生成图的DGAS性判定方法.令W=[e,Ae,…,An-1e]为图G的路矩阵(Walk-matrix),一个图G称为是可控图(Controllable graph)如果W非奇异.Godsil[48]猜想几乎所有图是可控制图，最近O’Rourke等[49]证明了该猜想成立.

Wang等[47]提出的方法主要基于以下观察：

定理4.1 令G是一个可控图,则一个图H与G广义A-同谱当且仅当存在唯一的一个有理正交矩阵Q,使得QTA(G)Q=A(H),Qe=e，其中e为分量权全为1的向量.

定理4.2[47]一个可控图G是DGAS的当且仅当Γ(G)仅包含置换矩阵.

由上述定理，若能证明Γ(G)中所有有理正交矩阵都是置换矩阵，则G是DGAS的.为证明这一点，定义一个有理正交矩阵的级为最小正整数l=l(Q),使得lQ为一个整数矩阵.显然一个满足Qe=e的有理正交矩阵Q是置换矩阵当且仅当它的级为1.进一步，若能证明∀Q∈Γ(G)，对任意素数p有p不能整除l(Q)，则一定有l=1，从而Q为置换矩阵.基于上述思想，Wang[50-51]得到了以下结果：

定理4.3 如果det(W)/2[n/2](该数总是整数)是无平方因子的奇数，则G是DGAS的.

Wang[50]对满足上述定理的随机图进行了大量数值试验，结果表明有大量的DGAS图存在(下界约为20%).

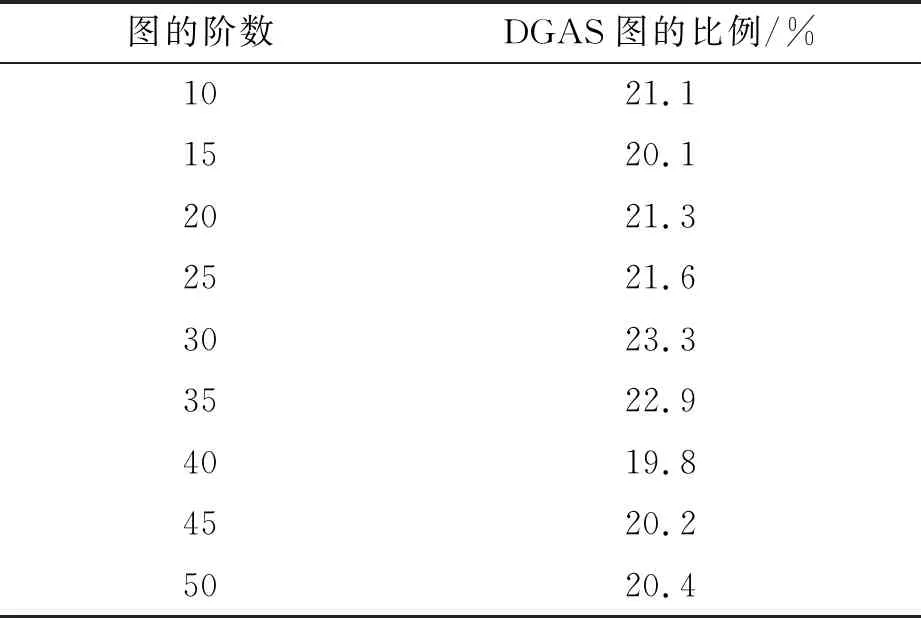
表1 DGAS图的比例

上述定理在一定意义下是最优的，即若det(W)/2[n/2]有平方因子，则一定条件下图G是非DGAS的.

定理4.4[52]令G为一个可控图，p为一个奇素数.假定以下条件成立：

(i)p2|det(W)；

(ii)W在有限域的秩rankp(W)=n-1；

(iii)方程组WTx≡0(modp)有下述形式的解：(1,1…,1,-1,-1,…,-1,0,0,…,0)T，其中1与-1的个数均为p.

则存在一个图H与G广义同谱且不同构.

类似的结果也可以对广义Q-谱(无符号拉普拉斯谱)成立.令WQ=[e,Qe,…,Qn-1e]为Q-路矩阵.

定理4.5[53]若det(WQ)/2[3n-2/2](该数总是整数)是无平方因子的奇数，则G是DGQS的.

关于DGAS图的构造，Mao等[54]及Liu等[55]给出了下述结果.令G∘K2为图G与K2的根积(即在G的每个顶点添加一个悬挂边得到的图),则有

定理4.6[54]若G的特征多项式的常数项为±1，且det(W(G))=±2n/2(n为偶数)，则G∘K2是DGAS的.

上述定理给出了显式构造无穷DGAS图序列的一个方法：从一个满足上述定理条件的小图G出发，不断构造G∘K2,(G∘K2)∘K2,…，则该序列中每个图都是DGAS的.

Liu等[55]给出了下述构造方法：从一个初始图G0出发，不断交替添加孤立顶点及取联(Join)，则G0满足一定条件下可以得到一个DGAS图的无穷序列.

关于图的广义谱确定性，可以提出以下问题：

问题1：如何判定非可控图的广义谱确定性？

问题2： 图的广义谱确定的有关结果是否可以推广至其他谱(譬如邻接谱、拉普拉丝谱等)？

问题3：能否证明广义谱确定图具有正的密度？

5 结束语

本文对图谱确定问题近年来的进展进行了简单的总结回顾，由于篇幅所限，很多相关话题未能涉及，所列结果也远非完全.目前该领域虽取得了很多进展，但仍有大量问题需要进一步研究，特别是Haemaer在2003年提出以下猜想——猜想(Haemers)：几乎所有图(关于邻接谱、拉普拉斯谱等)是谱确定的.

目前关于该猜想仍所知甚少，希望未来能发展出进一步的工具，对包括上述猜想在内的很多问题取得一些实质性的进展.