古诺映射的跟踪性质

廖 星， 汪火云， 易 鹏

(广州大学 数学与信息科学学院， 广东 广州 510006)

在本文中,一个动力系统就是一个偶对(Z,T),其中(Z,ρ)是一个带有度量ρ的紧致的度量空间,T:Z→Z是一个连续映射.设X和Y是两个度量空间，f:Y→X,g:X→Y是两个连续映射,设Φ:X×Y→X×Y被定义如下:Φ(x,y)=(f(y),g(x)),∀(x,y)∈X×Y,则(X×Y,Φ)是一个动力系统,称之为一个古诺双寡头模型,其中Φ被称为一个古诺映射,f和g是它的反应函数.特别地,当X和Y都是实数空间R的闭子区间时,称Φ为一个反三角映射.

古诺模型是由法国经济学家安东尼·奥古斯丁·库尔诺在1838年提出的,且在经济学的寡头理论和博弈论中得到了广泛应用.因此,引起许多学者对古诺映射的广泛关注,他们研究古诺映射的动力学性质[1-4],如混沌、ω-极限集和周期性等.本文研究古诺映射的跟踪性质和链混合性质等,得到如下结论:古诺映射Φ有伪轨跟踪性质(平均跟踪性质)当且仅当f∘g和g∘f也有伪轨跟踪性质(平均跟踪性质);古诺映射Φ是链混合的当且仅当f∘g和g∘f也是链混合的;此外,证明了反三角映射Φ是链传递的(拓扑混合的)当且仅当f∘g和g∘f也是链传递的(拓扑混合的);最后,举了一个f∘g和g∘f是链传递的,而Φ不是链传递的例子.

1 基本概念

首先介绍本文所用到的相关概念.

令N={0,1,2,3,…}是自然数集,N+={1,2,3,…},R是实数集.设(Z,T)是一个动力系统,如果对Z中的任意两个非空开集U,V,存在正整数m,使得Tm(U)∩V≠φ,则称T是拓扑传递的.如果对Z中的任意两个非空开集U,V,存在正整数M,使得对任意正整数n≥M,有Tn(U)∩V≠φ,则称T是拓扑混合的.

设(Z,T)是一个动力系统,z∈Z,如果存在递增序列ni,使得

则把点y叫做z的ω-极限点(y∈Z)，并称z的全体ω-极限点的集合为z的ω-极限集,记作ω(z,T).

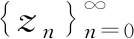
ρ(T(zn),zn+1)<δ.

设a=z0,z1,…,zn-1=b为Z中的有限序列,如果对每一个i∈{0,1,…,n-2},有

ρ(T(zi),zi+1)<δ,

则称a=z0,z1,…,zn-1=b是一条从a到b长度为n的T的δ-链.

设(Z,T)是一个动力系统,如果对任意a,b∈Z,δ>0,存在一条从a到b的T的δ-链,则称T是链传递的.如果对所有正整数n≥1,Tn是链传递的,则称T是完全链传递的.如果对任意a,b∈Z,δ>0,存在正整数M,使得当n≥M时,存在一条从a到b长度为n的T的δ-链,则称T是链混合.

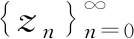
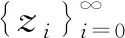
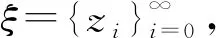
那么也称点z′,ε-平均跟踪ξ.

2 结果的证明

古诺映射有如下基本性质:

(1)Φ2(x,y)=Φ(f(y),g(x))=(f∘g(x),g∘f(y));

(2)对任意正整数n,Φ2n(x,y)=((f∘g)n(x),(g∘f)n(y));

(3)对任意正整数n,Φ2n+1(x,y)=((f∘g)n∘f(y),(g∘f)n∘g(x)).

以下结果参见文献[6]第15章中的定理4.3和定理4.5.

引理2.1设(Z,T)是一个动力系统,则下列命题成立:

(1)T有伪轨跟踪性质,则对任意正整数k,Tk也有伪轨跟踪性质.

(2)若存在一个正整数k,使得Tk有伪轨跟踪性质,则T也有伪轨跟踪性质.

以下结论参见文献[7]中的引理3.2.

引理2.2设(Z1,T1)和(Z2,T2)是两个动力系统,则T1×T2有伪轨跟踪性质当且仅当T1和T2也有伪轨跟踪性质.

命题2.1设Φ(x,y)=(f(y),g(x))是一个古诺映射,其中f:Y→X,g:X→Y都是连续映射,(x,y)∈X×Y，则Φ有伪轨跟踪性质当且仅当f∘g与g∘f也有伪轨跟踪性质.

证明(必要性)设Φ有伪轨跟踪性质,由引理2.1(1),Φ2=(f∘g)×(g∘f)也有伪轨跟踪性质.再由引理2.2,f∘g与g∘f也有伪轨跟踪性质.

(充分性)若f∘g与g∘f有伪轨跟踪性质,由引理2.2,则Φ2=(f∘g)×(g∘f)也有伪轨跟踪性质.由引理2.1(2),从而Φ有伪轨跟踪性质.

命题2.2设Φ(x,y)=(f(y),g(x))是一个古诺映射,其中f:Y→X,g:X→Y都是连续映射,(x,y)∈X×Y，则Φ有平均跟踪性质当且仅当f∘g与g∘f也有平均跟踪性质.

证明(必要性)设Φ有平均跟踪性质,由文献[8]中的引理3.3知Φ2=(f∘g)×(g∘f)有平均跟踪性质,从而f∘g与g∘f也有平均跟踪性质.

(充分性)设f∘g与g∘f有平均跟踪性质，由文献[8]中的命题3.5知，(f∘g)×(g∘f)有平均跟踪性质,从而Φ2=(f∘g)×(g∘f)也有平均跟踪性质,根据文献[9]中的引理3.4、引理3.5和定理5.5,可知Φ有平均跟踪性质.

以下引理参见文献[10]中的推论12.

引理2.3设(Z,T)是一个动力系统,则T是链混合的当且仅当T是完全链传递的.

以下引理参见文献[11]中的定理2.

引理2.4设(Z,T)是一个动力系统.若存在一个正整数k,使得Tk是链传递的,则T是链传递的.

命题2.3设(Z,T)是一个动力系统.

(1)若T是链混合的,则对任意一个正整数k,Tk也是链混合的.

(2)若存在一个正整数k,使得Tk是链混合的,则T也是链混合的.

证明(1)若Tk不是链混合,由引理2.3,存在一个正整数m,使得(Tk)m不是链传递的.又因为T是链混合的,由引理2.3,对任意正整数n,Tn是链传递的,这与(Tk)m不是链传递的矛盾,故Tk是链混合的.

(2)若T不是链混合的,由引理2.3,存在一个正整数m≠k,使Tm不是链传递的,又因为Tk是链混合的,由引理2.3,(Tk)m=(Tm)k是链传递的.由引理2.4,则Tm是链传递的,与假设矛盾,故T是链混合的.

命题2.4设Φ(x,y)=(f(y),g(x))是一个古诺映射,其中f:Y→X,g:X→Y都是连续映射,(x,y)∈X×Y.则Φ是链混合的当且仅当f∘g与g∘f也是链混合的.

证明(必要性)若Φ是链混合的,由命题2.3(1),Φ2=(f∘g)×(g∘f)是链混合的,故f∘g与g∘f是链混合的.

(充分性)若f∘g与g∘f是链混合的,则Φ2=(f∘g)×(g∘f)也是链混合的,由命题2.3(2),故Φ是链混合的.

以下结论参见文献[10]中的推论14.

引理2.5设Z是一个连通空间的，且T:Z→Z连续映射.则T是链传递的当且仅当T是链混合的.

推论2.1设Φ(x,y)=(f(y),g(x))是一个反三角映射,其中f:Y→X,g:X→Y都是连续的,(x,y)∈X×Y,且X,Y是R的闭子区间.则Φ是链传递的当且仅当f∘g与g∘f也是链传递的.

证明因为X,Y是R的闭子区间，故X×Y空间也是连通的.由引理2.5,则Φ是链传递的与Φ是链混合相互等价.根据命题2.4,有Φ是链传递的当且仅当f∘g与g∘f也是链传递的.

以下引理参见文献[12]中的定理1.

引理2.6假设T是区间上的一个连续映射,则T是拓扑混合的当且仅当对任意正整数n,Tn是拓扑传递的.

命题2.5设Z是R是的一个闭子区间,T:Z→Z是连续映射,则下面的结论成立:

(1)若T是拓扑混合的,则对任意一个正整数k,Tk是拓扑混合的.

(2)若存在一个正整数k,使得Tk是拓扑混合的,则T是拓扑混合的.

证明(1)假设T是拓扑混合的,由引理2.6,对任意正整数n,Tn是拓扑传递的.故对任意正整数m,(Tk)m=Tkm是拓扑传递的.再由引理2.6,故Tk是拓扑混合的.

(2)若T不是拓扑混合的,由引理2.6,存在一个正整数m≠k,使得Tm不是拓扑传递的.由于Tk是拓扑混合的,由引理2.6,(Tk)m=(Tm)k是拓扑传递的.故Tm是拓扑传递的,与假设矛盾,故T是拓扑混合的.

命题2.6设Φ(x,y)=(f(y),g(x))是一个反三角映射,其中f:Y→X,g:Y→X都是连续的,(x,y)∈X×Y,且X,Y是R的闭子区间.则Φ是拓扑混合的当且仅当f∘g与g∘f也是拓扑混合的.

证明(必要性)设Φ是拓扑混合的,由命题2.5,Φ2是拓扑混合的.由于Φ2=(f∘g)×(g∘f),故f∘g与g∘f是拓扑混合的.

(充分性) 若f∘g与g∘f是拓扑混合的,有Φ2是拓扑混合的.由命题2.5,故Φ是拓扑混合的.

最后,给出一个Φ是链传递的(拓扑传递的)和f∘g与g∘f是链传递的(拓扑传递的)并不是等价的例子.

例设Φ(x,y)=(f(y),g(x))是X×X上的古诺映射,其中X={1,2,3},令f(1)=g(1)=2,f(2)=g(2)=3,f(3)=g(3)=1,则其中f:X→X,g:X→X都是连续映射.由于有

f∘g(1)=g∘f(1)=3,f∘g(3)=g∘f(3)=2,f∘g(2)=g∘f(2)=1，

故f∘g与g∘f是拓扑传递的,因而它们是链传递的.取x=1,y=2,则有

ω((1,2),Φ)={(3,1),(2,1),(2,3),(1,2),(1,3),(3,2)}.

从而Φ不是传递的,易知Φ也不是链传递的.