基于双链染色体结构的遗传算法研究*

钱 菲，陈贤富

(中国科学技术大学 信息科学技术学院，安徽 合肥 230026)

0 引言

遗传算法作为一种全局优化搜索算法，是模拟生物进化过程中“适者生存”的计算模型。传统的遗传算法使用简单，鲁棒性强，易于并行化，因而应用研究已从初期的组合优化求解扩展到了许多高新工程化的应用方面[1]。

但是，传统遗传算法的局部搜索能力差，容易出现早熟收敛现象[2]。而且每个个体都是用一条染色体表示,这种通过单个变量的遗传操作只有染色体的交叉、变异和复制却没有基因的分离重组的过程，不仅难以表示很多实际应用的对象，而且会造成模式的丢失，不利于保持种群多样性[3]。本文针对这些不足，对其进行了改进，引入了更加符合生物特性的双链染色体，并重新定义了染色体的重组、交叉和变异操作。

1 双链染色体模型

双链染色体模拟生物学中的二倍体结构，即含有两个同源染色体组。每个同源染色体组的两个染色单体分别来自于父母，组成姐妹染色单体。如图1所示，二倍体的生物遗传主要通过同源染色体组的非姐妹染色单体之间交叉互换实现基因重组，因此维持了生物特性的世代相传。本算法中双链染色体特有的“双链”结构具有冗余记忆能力，不仅能够更好地保留上代的优质基因，而且扩大了基因所携带的信息量，较单倍体单链结构而言具有更强的适应能力[4-6]。

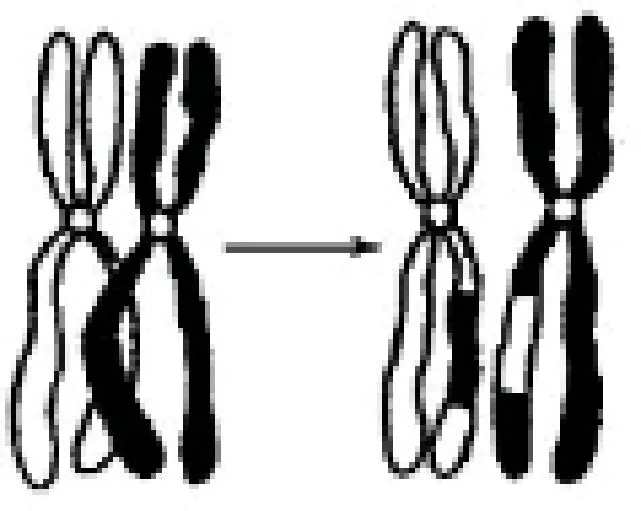
图1 同源染色体交叉互换

2 基于双链染色体结构的遗传算法

基于双链染色体结构的遗传算法比传统遗传算法多出了一组基因信息[7]，因此将传统遗传算法的选择、交叉、变异操作应用到基于双链染色体结构的遗传算法上时需要进行改进。为了模拟生物繁殖的特性，引入染色体分离重组操作，并用自适应交叉方式来强调两个基因链的共同作用。为了防止优质基因丢失，提出挑选子代再变异和最优个体保存操作[8]。

2.1 染色体分离重组

染色体分离重组就是依照孟德尔分离定律将父代的双链染色体拆分成四个配子，然后将配子重新组合产生四个新的子代，如图2所示。本文将配子称为基因链，而每个子代都是由含有父代信息的杂型基因链重组而成，不仅很好地保持了基因信息的传递，而且增加了种群多样性，为交叉操作做好准备。

图2 染色体分离重组

2.2 自适应交叉

交叉操作使得遗传算法具有全局搜索能力，是区别于其他传统优化方法的重要标志。常见的交叉方式有一点交叉、两点交叉、多点交叉和一致交叉等。区别于基本遗传算法的交叉策略，本文提出了自适应交叉方式，以提高搜索效率。自适应交叉是将与或交叉与两点交叉相结合。与或交叉对基因链的模式破坏作用大，能非常好地提高搜索速度，加速收敛。但是这种交叉方式往往会出现偏0或偏1，导致种群多向性降低。因此在此基础上结合对基因链的模式破坏作用不大的两点交叉，即当采用与或交叉出现种群多样性下降明显时换用两点交叉。

2.3 挑选子代再变异

为了提高局部随机搜索能力，维持种群的多样性，提出了挑选子代再变异的操作。根据与或交叉的性质，个体的优秀基因可能存在于适应度高的个体中，也有可能在适应度低的个体中。因此在与或交叉后挑选基因链中适应度较高和较低的两个子代作为遗传对象来更新种群，其他的全部淘汰。对于两点交叉，是在种群多样性下降明显时自适应采用的，因此在选择较高适应度的三条基因链后再随机生成一条基因链组成两个新个体来更新种群。这样不仅能扩大局部搜索范围，而且维持了种群多样性，能较好地抑制算法出现局部最优解。

2.4 最优个体保存

更新种群时为了防止适应度较高的个体被淘汰，本文根据双链染色体特有的“双链”结构，提出了保存最优个体的策略：

(1)如果更新子代时，子代最优个体基因链的适应度超过父代最优个体基因链，则子代最优个体为新的最优个体；

(2)如果更新子代后，子代的最优个体基因链的适应度未超过父代最优个体基因链，则将父代的最优个体基因链放进子代的最差个体基因链中，组成新的最优个体。

2.5 算法步骤

(1)初始化种群，设置控制参数，令最大进化代数为G，进化代数变量为g=0。

(2)对初始种群进行适应度计算和多样性计算，标记最优、最差种群个体信息，然后进行染色体的遗传配对，更新子代。

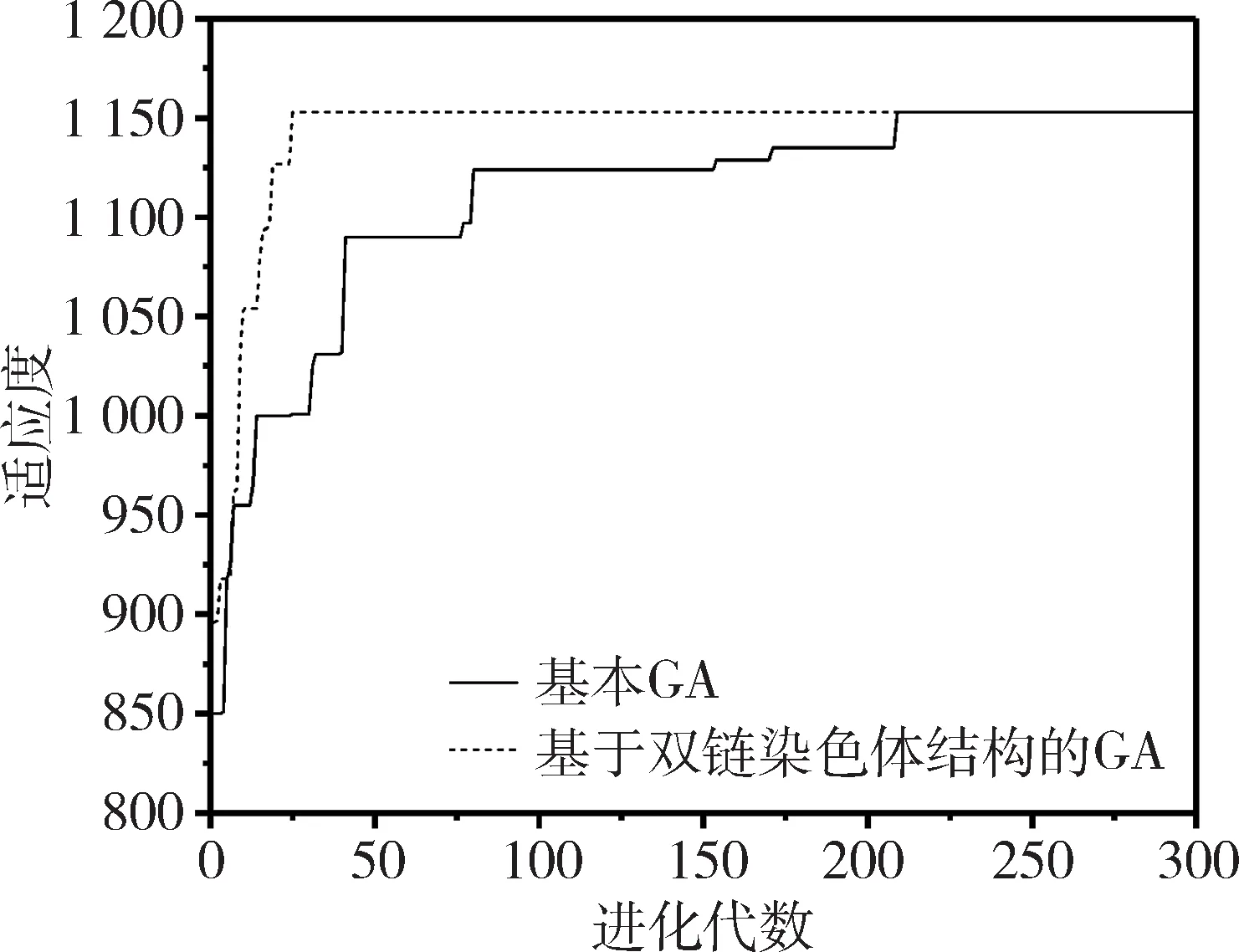
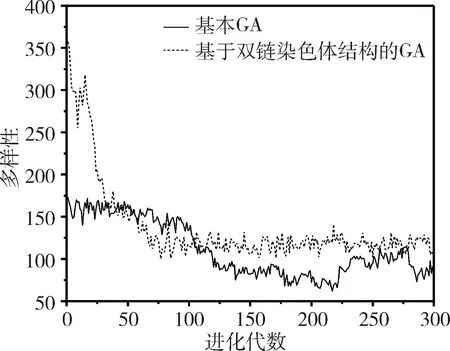
(3)判断g与G的大小关系，如果g

(4)选择两个个体进行染色体分离重组，根据当前种群的多样性，对重组后的个体进行基因链的自适应交叉。

(5)计算交叉后所有基因链的适应度并排序，然后按适应度值挑选基因链组合成新的子代在进行变异。

(6)判断新种群个体数是否小于种群规模。若是，则转步骤(4)，继续循环；若不是，则继续。

(7)统计生成的新一代种群适应度。

(8)对新旧种群的最优个体进行比较，保存最优个体基因链。

(9)更新种群，统计适应度和多样性，转步骤(3)。

3 实验分析

为了能够验证基于双链染色体结构的遗传算法比传统遗传算法具有一定的优势，将两者进行试验比较。同时用两者解决50个货物的背包问题，从算法质量、收敛速度和种群多样性三个方面进行分析。

实验环境为Windows 7 64位操作系统，使用Visio Studio 2013，采用C++语言编码实现。

实验中设置各控制参数如下：最大遗传代数为300，选取交叉概率为0.5，变异概率为0.07，种群规模为200，染色体长度为50，比较基于双链染色体结构的遗传算法和基本遗传算法的计算结果质量和收敛速度，如图3所示。

图3 适应度对比图

由图3可知传统遗传算法收敛速度慢，而且容易出现局部最优解，如果进化代数不够，很难找到一个满意的解，算法质量比较差。而本算法能以较快的收敛速度达到全局最优解，基本没有出现局部最优的过渡，这样无需进化很多代就能找到一个满意的解。

种群多样性是影响种群发展的重要因素之一。随着进化的推演，种群的多样性会随之降低。而且不同的进化方式对种群的多样性影响不同。对比两种算法的种群多样性，如图4所示，能看出本算法在初期因为其特有的双链结构，其多样性是基本遗传算法的2倍，但进化一定代数后，多样性急速下降后维持稳定。这是由于进化初期使用与或交叉方法所导致的。虽然多样性在这阶段下降明显，但对比图3可以知道，本算法在前期已经收敛，而且种群的平均多样性明显高于传统遗传算法。

图4 多样性对比图

从图3、图4的结果显示可知，由于染色体“双链”结构的特殊性，本算法在收敛速度、计算结果的质量和种群多样性的表现上都有明显的改进。

4 结束语

本文提出的改进算法基于染色体的“双链”结构，引入染色体分离重组、自适应交叉、挑选子代再变异和最优保存策略的操作。经试验表明，本算法不仅有效抑制了算法的早熟现象，提高收敛速度，而且维持了种群的多样性。

但本算法遗留的一个重要问题是自适应交叉操作的分界点问题。在算法操作中根据多样性下降明显的点进行变换交叉方式，但左右移动分界点对结果有明显影响。后续将继续研究自适应交叉方式的分界点问题，并将该改进算法应用到巨灾情景构建及应急能力评估模型优化上。