基于电压矢量注入的表贴式永磁同步电机转子初始位置检测
李向舜,周 贺,李启东,刘 涛
(1.武汉理工大学 自动化学院,武汉 430070 ;2.华中科技大学 光学与电子信息学院,武汉 430074)
0 引 言
在永磁同步电机(PMSM)无位置传感器控制中,对电机的高性能控制依赖于精确的转子位置,而获取转子初始位置则是电机顺利起动的前提,若无法准确检测转子初始位置,则无法正确选择合适的电压空间矢量,就可能造成电机过流或发生反转[1-3]。
目前针对PMSM转子初始位置检测的方法很多,各有利弊。预定位置法通过向PMSM中注入一个固定角度的电流矢量,从而将转子拖动到预定的位置,该方法的缺点是精度受负载影响较大,而且运行时转子需要旋转[4]。对于具有明显凸极效应的内嵌式永磁同步电机(IPMSM),可以使用高频信号注入法检测转子初始位置,但对于隐极结构的表贴式永磁同步电机(SPMSM),由于凸极效应不明显,该方法实现难度较大[5-8]。基于此,文献[9-10]提出了基于磁路饱和效应的电压矢量注入法,通过向电机注入一系列不同角度的电压矢量,通过检测电流响应来获取SPMSM转子初始位置。但在实践中,该方法还存在检测周期长,准确性低,甚至转子旋转的问题。
本文从SPMSM在电压矢量注入下的数学模型出发,分析了矢量注入方向的电流响应形式,以及影响位置辨识成功的因素,提出三轮检测法,通过优化电压幅值、检测策略,分步有序的检测初始位置,仿真和实验结果表明,该方法可以准确、快速的检测转子初始位置,并能保持转子静止。
1 转子初始位置检测原理
1.1 SPMSM电压矢量注入模型
为便于分析SPMSM,假设定子磁场呈正弦分布,不计涡流损耗和磁滞损耗等,采用id=0的矢量控制,在dq轴系下的电压方程为:
(1)
式中,ud、uq分别为d、q轴电压;id、iq分别为d、q轴电流;Ld、Lq分别为d、q轴电感;Rs为定子电阻;ψf为永磁体与定子交链的磁链;ωr为转子的电角速度;p为微分算子。
在零速时,可忽略式(1)中的交叉耦合项和反电动势部分,dq轴系下的电压方程简化为
(2)

图1 电压矢量注入示意图
如图1所示,在电机保持静止状态下,向电机注入一定幅值,有限作用时间的电压矢量,该矢量与真实d轴方向的夹角为φ,则式(2)可表示为
(3)
根据式(3),可求得id、iq:
(4)

(5)
对处于磁路饱和的SPMSM,定子d轴电感是与φ有关的函数[11],其函数关系如图2所示。当φ=±π/2时,定子绕组与转子永磁体交链的磁通最少,磁路最不饱和,Ld(φ)达到极大值。当时φ=0,π定子绕组与转子永磁体交链的磁通最多,磁路饱和度最高,Ld(φ)达到极小值。注意到,由于电机饱和凸极效应,对电机d轴的N和S极分别注入电压矢量,当φ=0时,电流产生的磁场和转子磁场方向相同,具有增磁作用,当φ=π时,产生去磁作用,因此当φ=0时,电感更容易饱和,导致此时电感值略小于φ=π的电感值。另外,q轴磁路处于不饱和状态,可将其视为常数Lq。
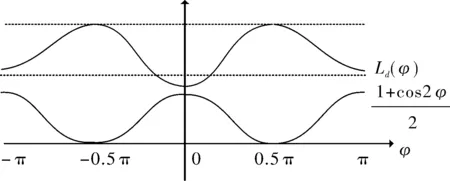
图2 d轴电感变化曲线


图变化曲线
1.2 位置辨识成功的影响因素分析
将式(5)简化为
(6)

2 转子初始位置检测方法
考虑实际使用工况,在检测过程中,首先转子应保持静止,其次尽量减少检测过程所需时间,尽可能提高检测精度和准确度。
为了保持转子静止,同时减少电流下降到零的时间,在每次电压矢量注入结束后,再向其反方向注入相同幅值、相同作用时间的电压矢量。同时注意到,当夹角φ接近±π/2时,较大的电磁转矩可能导致转子旋转,因此电压矢量幅值要选择适当,既要能满足转子静止,又能使电机产生饱和凸极效应。而在鉴别NS极时,需要增大电压矢量的幅值,加深电感的饱和度。基于此,提出采用三轮检测法,分步有序的检测位置。

图4 初始位置检测框图
初始位置检测框图如图4所示,假设转子初始位置为40°,检测步骤如下:
第一轮:粗略检测位置
如图5所示,将360°电角度分为6个扇区,采用“顺序法”,依次在每个扇区中间位置注入幅值为u1,作用时间为Δ1的电压矢量,该电压矢量幅值可以适当取小。在执行第一步检测后,将能够获得转子NS极所在扇区,对于可能出现的NS极判断出错,则会在第三轮重新判断。
第二轮:精确检测位置
选择NS极所属扇区中的一个扇区,在该扇区内选择“二分法”精确检测位置。如图5所示,在15°,30°,45°方向上同样注入幅值为u2,作用时间为Δ2的电压矢量,比较15°,30°,45°方向上的大小,如果得到45°方向上较大,则继续在37.5°,52.5°上同样注入幅值为u2,作用时间为的电压矢量,依次类推,所在方向即为转子精确位置。
第三轮:鉴别NS极
为了准确鉴别NS极,在第二轮已得到精确位置的正反方向上,分别注入幅值为u3,时间宽度为Δ3的电压矢量,该电压幅值u3应较大。较大所在方向即为N极方向。

图5 电压矢量施加顺序图
3 仿真分析
为验证该方法的有效性,以一台表贴式永磁同步电机为研究对象,在Simulink中搭建了具有饱和凸极效应的SPMSM仿真模型,该电机主要参数为:PN=1500W,UN=110V,IN=12A,Ld=Lq=13.5 mH,Rs=0.9 Ω,p=3,J=0.00351 kg·m2按照三轮检测法,对该电机进行了仿真分析。
在每次电压矢量注入结束后,向其反方向注入相同幅值、相同作用时间的电压矢量,并继续注入相同时间的零矢量,以确保电流降为零,为下次矢量注入做好准备,假设转子初始位置为40°:
第一轮:u1=0.2Udc,Δ1=400 μs,从图6(a)可知,30°和210°方向上最大,并且两者差值很小,需要进一步判断NS极。同时由于反向电压矢量的注入,电流可以快速衰减到零。
第二轮:u2=0.4Udc,Δ2=400 μs,从图6(b)可知,37.5°方向上最大,值随着夹角φ的增大而逐渐变小。
第三轮:u3=0.8Udc,Δ3=400 μs,从图6(c)可知,在将电压幅值扩大四倍后,正反向电流差值更大,可以准确判断出NS极。
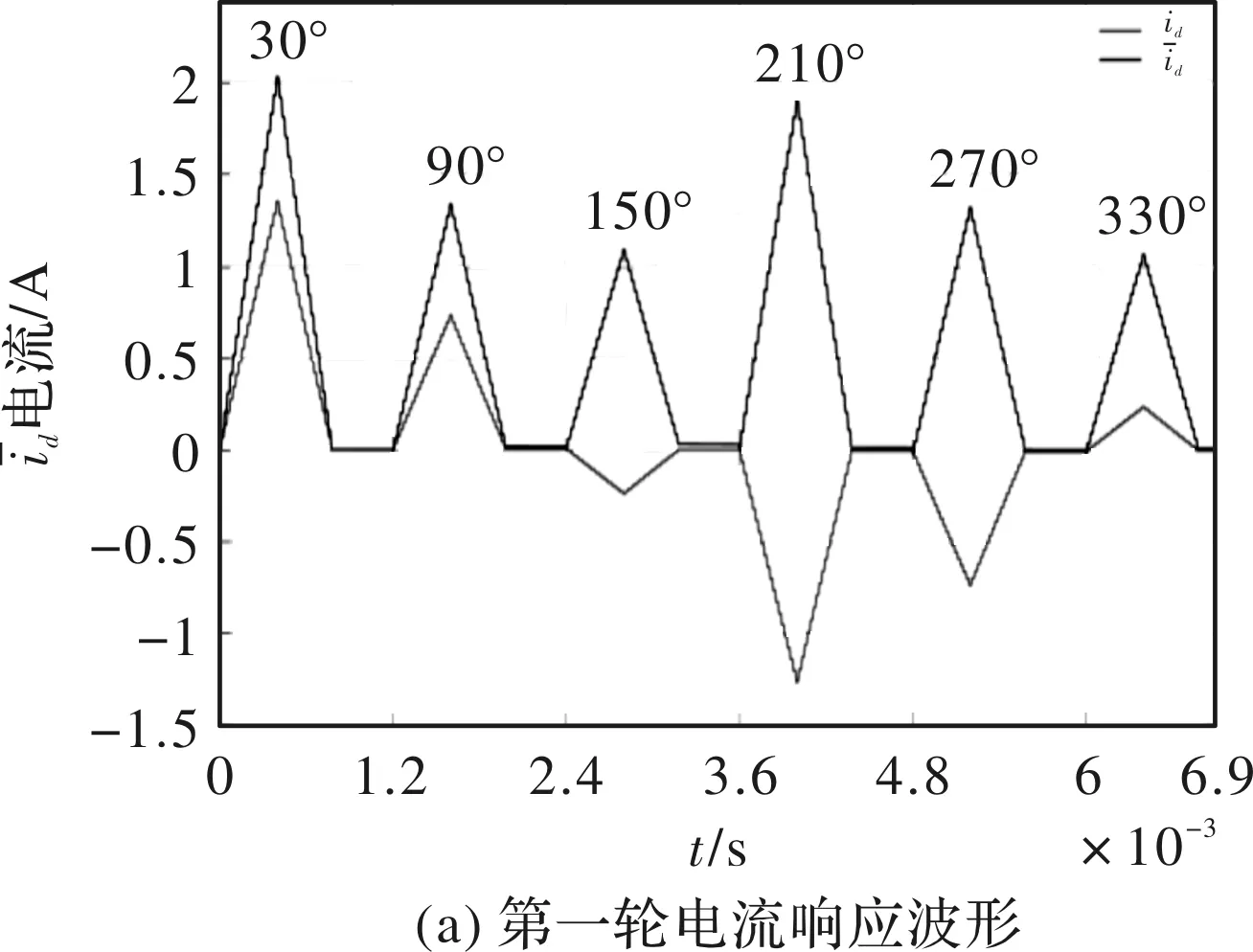
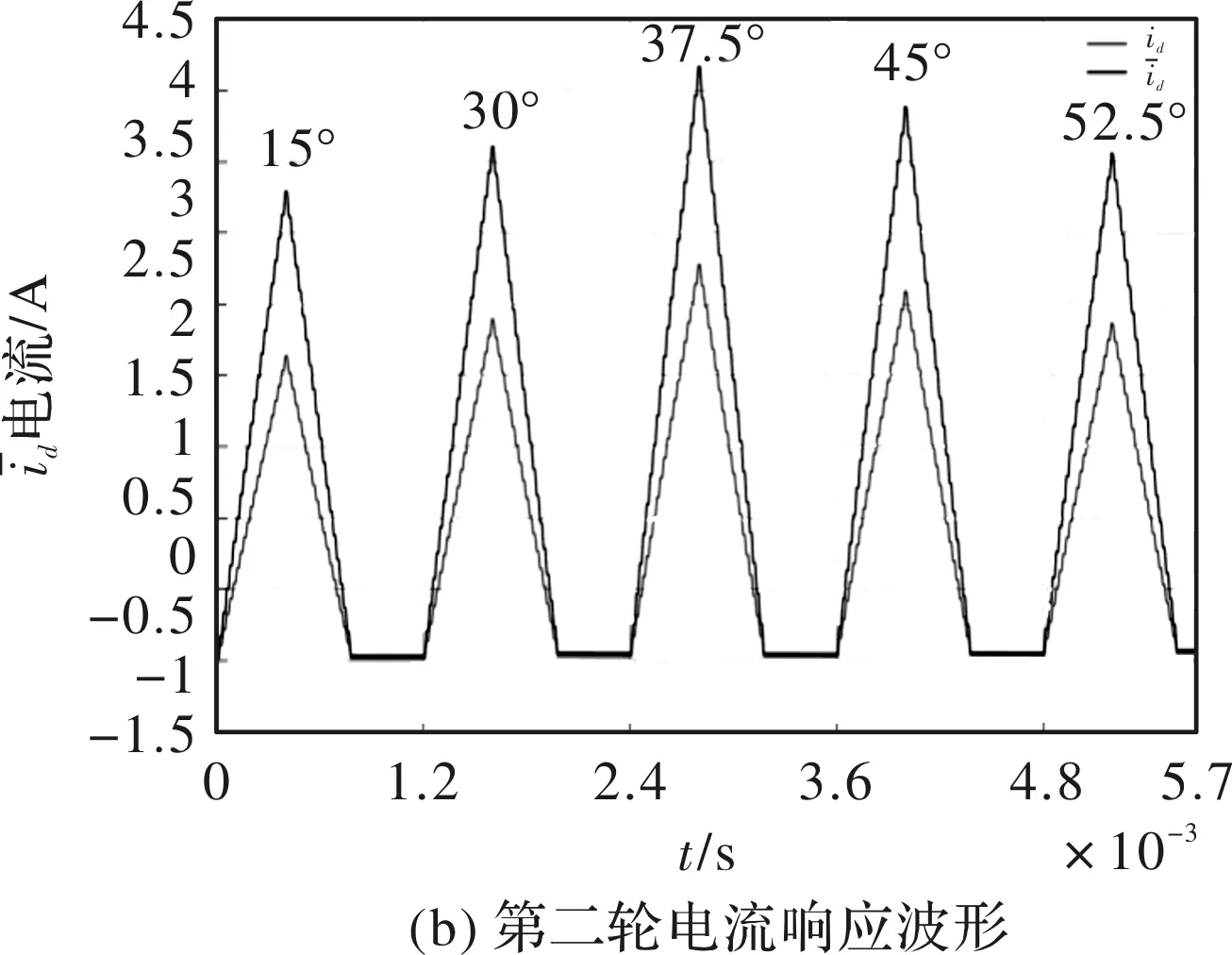

图6 电流响应仿真波形
图7为检测过程中电机转动角度曲线。转子转动最大角度仅为0.42°,并且发生在第一轮检测过程中,在第二、三轮中,虽然增大了电压矢量幅值,但由于转矩较小,所以转动角度较小。因此在粗略估计出转子位置后,可以适当增大电压矢量幅值,加深电感饱和程度,而不会引起转子大范围转动。

图7 转动角度曲线
4 实验分析
在仿真验证的基础上,进行了大量实验。控制系统以MKV31F128为核心,开发环境为keil-MDK,首先用磁场定向法将电机转子拖动到40°,然后执行三轮检测,检测结果如下:
图9为A相电流响应波形。在整个检测过程中,转子一直稳定在初始位置,仅表现为轻微震动,并未发生旋转现象。



图8 电流值

图9 相电流响应波形
5 结 语

针对传统电压矢量法检测周期长、准确性低、和转子旋转的问题,本文所提的三轮检测法,通过优化电压幅值、检测策略,可以准确、快速的检测转子位置,并能保持转子静止,该方法也同样适用于IPMSM初始位置检测。

