驱动模式对步进电机转矩和噪音的分析

彭 震，毕 超

(上海理工大学 机械工程学院，上海 200093)

0 引 言

电机运行时的噪声源可分为3个方面：与电机机械结构有关、与电机电磁结构有关和与驱动电路有关。这里不讨论由机械原因引起的噪音。而由电机电磁结构相关的原因包括齿槽转矩和单边磁拉力，这些也不在本文的讨论范围。由驱动电路引起的噪声则比较复杂，不合理的电流波形会产生电磁转矩脉动，进而引起电机的噪音[1]。

步进电机中转矩脉动的产生是由于步进电机特有的结构和驱动方式，导致电机相电流含有高次谐波分量，使得电磁转矩产生波动。

显然，电磁转矩形成的噪音包含了转矩脉动的信息。因而，可以通过对电机噪音的检测了解驱动电流对转矩的影响。对于混合式步进电机而言，其磁极对数较多，高次谐波转矩的影响较大。这些高次谐波的转矩脉动很难用测功机这样的接触式装置对转矩进行直接测量。而对噪音的测量是非接触式的，其结果可以了解到电机的驱动模式对电机的转矩脉动的影响，并且能够了解到产生噪音的多种电磁和机械原因。

1 谐波电磁转矩脉动

步进电机需要用脉冲电流来驱动，在正常情况下，利用控制脉冲的个数、频率和细分步数的计算来准确获得电机转子的位置与转速[2]。

谐波电磁转矩的存在会导致步进电机产生振荡分量，进而影响电机的正常运行。

单相通电时，二相混合式步进电机的磁路模型[3]：

ψmk=2Λ1WFmcosθe

(1)

式中，ψmk为转子永磁体与第k相绕组的交互磁链；Λ1为磁导的基波分量幅值；W为磁能；Fm为永磁体的等效磁动势；θe为转子的电角位移。若不计磁滞和涡流损耗，忽略磁路饱和，则电磁转矩Tk可表示为

(2)

式中，Zr为转子齿数；ik为第k相绕组的相电流；θ=θe/Zr，θ为转子的机械角位移。将式(1)代入式(2)中，即可得到混合式步进电机单相通电时电磁转矩Tk的基波Tk1为

Tk1=-2ZrΛ1WFmiksinθe=-Ktiksinθe

(3)

式中，Kt=2ZRΛ1WFm为电动机的转矩系数。k=A,B。实际上，对于工业产品的步进电机，其电磁转矩Tk，除了含有如式(3)所示的基波外，还含有一定的高次谐波分量。

根据叠加定理，多相通电时，电机的矩角特性近似地可以由每相各自通电时的矩角特性叠加求出。由于二相混合式步进电机的两相绕组正交，所以电机A相和B相的电磁转矩的基波为

(4)

当二相混合式步进电机绕组中的电流按如下规律变化：

(5)

式中，I为绕组电流幅值。则A、B两相同时通电时的合成电磁转矩为

TAB=TA+TB=KtI

(6)

由以上公式得知：如果仅考虑矩角特性的基波分量，要想消除电磁转矩脉动，须通入变化规律为式(5)的驱动电流，但在实际驱动中，给驱动器输入的是方波电流，其含有大量的高次谐波。而如果考虑到矩角特性的高次谐波分量，高次谐波的电流对转矩的影响就更加复杂，也就进一步引发电机振动和噪音。因此采用细分功能的驱动器来改善电流波形，抑制电流谐波，对减少电机运行噪音是有帮助的[4]。

2 步进电机的噪音来源

由电磁转矩脉动产生的噪音的基频表达式可以写成

(7)

式中，fith为电机基波频率第ith次谐波分量，i为谐波次数，p为步进电机的极对数(即步进电机转子齿数)，n为转速。

步进电机是在不同频率的脉冲控制下，按一定的逻辑状态循环通电而运转的，因此存在两种基本电磁周期，一个是控制脉冲周期[5]：

Tcp=1/fcp

(8)

另一个是每相绕组的脉冲电压或电流基波周期，绕组电压、电流的相基波频率为f相，基波周期即

T相=1/f相

(9)

其中，控制脉冲频率与绕组电压、电流基波频率存在如下关系

f相=fcp/N

(10)

式中，N为一个整数，是一个通电逻辑循环的通电状态数，即电机的运行拍数。两相步进电机整步运行时为4拍，半步运行时为8拍。依次类推各细分下的运行拍数。

两相步进电机的矩角特性近似地可以由每相各自通电时的矩角特性叠加求得。如果只考虑矩角特性的基波分量，理论上无数次的细分将将使得两相空间正交的绕组中的在时域上正交的电流越来越接近正弦，也就没有谐波转矩分量，电机就不会发生谐波振荡。

图1 实验系统

3 步进电机噪音实验

本实验控制芯片使用的是TI公司的TMS320F28335DSP，通过Epwm产生的PWM波来作为控制二相混合式步进电机的驱动脉冲信号。配套的驱动器是应用电流波形控制的细分驱动器，使得电机可以在各细分状态运行。

功放部分采用H桥双极性驱动电路，特点是通过电流波形的设定和采样，在每一个恒频斩波周期内将实际电流与设定电流信号进行PWM比较，进而控制电路的上下桥臂，进行恒频斩波以实现电流波形的控制[5]。其原理图如图2所示。在实际应用中，图中的开关是用MOS管来代替。

图2 H桥电路原理图

在实验过程中，步进电机分别在8拍、32拍和64拍方式下运行，使电机转速以20 r/min的增量由400 r/min增加至800 r/min,电机和麦克风一直处于噪音隔离的噪音箱中，麦克风通过声卡连接上位机对电机噪音进行采集。将采集到的数据进行快速傅里叶分析(FFT)，即可得到电机的噪音瀑布图。

瀑布图分析是旋转机械振动噪声分析最常用的方法，它采用“跳跃式的FFT变换”方式计算瞬时频谱，并用叠加的方法把各个转速下的噪音频谱用一张图来显示，从中可以看到各种电磁和机械原因所引起的噪音，是一种非常有效的检测工具。

3.1 绕组电流

步进电机在8拍、32拍和64拍运行方式下的定子绕组电流如图3所示。

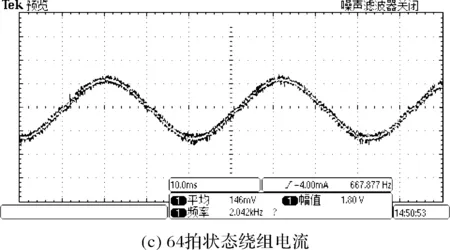
图3 绕组电流

从图中可以看出，步进电机整步运行时，其定子绕组电流是一个一个的脉冲，但在整步运行下，电机容易出现低频失步和低频振荡导致电机无法正常运转。采用细分控制，对电机的步距角进行细分，使其绕组电流按阶梯状上升，并且逐渐趋近于正弦波。如前所叙，如果二相步进电机的每相电流所产生的矩角特性是正弦的，在空间域为正弦分布的两相正交的电流可以产生恒定的转矩，这应当使电机运行更加平稳，电机噪音得以减小。

3.2 噪音瀑布图

在上位机用GoldWave软件对电机的噪音信息进行采集，将采集的音频数据做傅里叶分析，得到电机在8拍运行方式下的噪音瀑布图如图4所示。其展示了一个完整的噪音瀑布图，它包含了：低频振荡噪音和谐波噪音部分(椭圆1)，电机共振频率部分(椭圆2)和斩波频率部分(椭圆3)。

图4 完整噪音瀑布图

图5可以看出在靠近纵坐标轴的部分，转矩脉动幅值较大，噪音混乱，这是电机的低频振荡区，与机械结构、轴承结构和风道结构和等因素相关，也与电流的谐波有关。

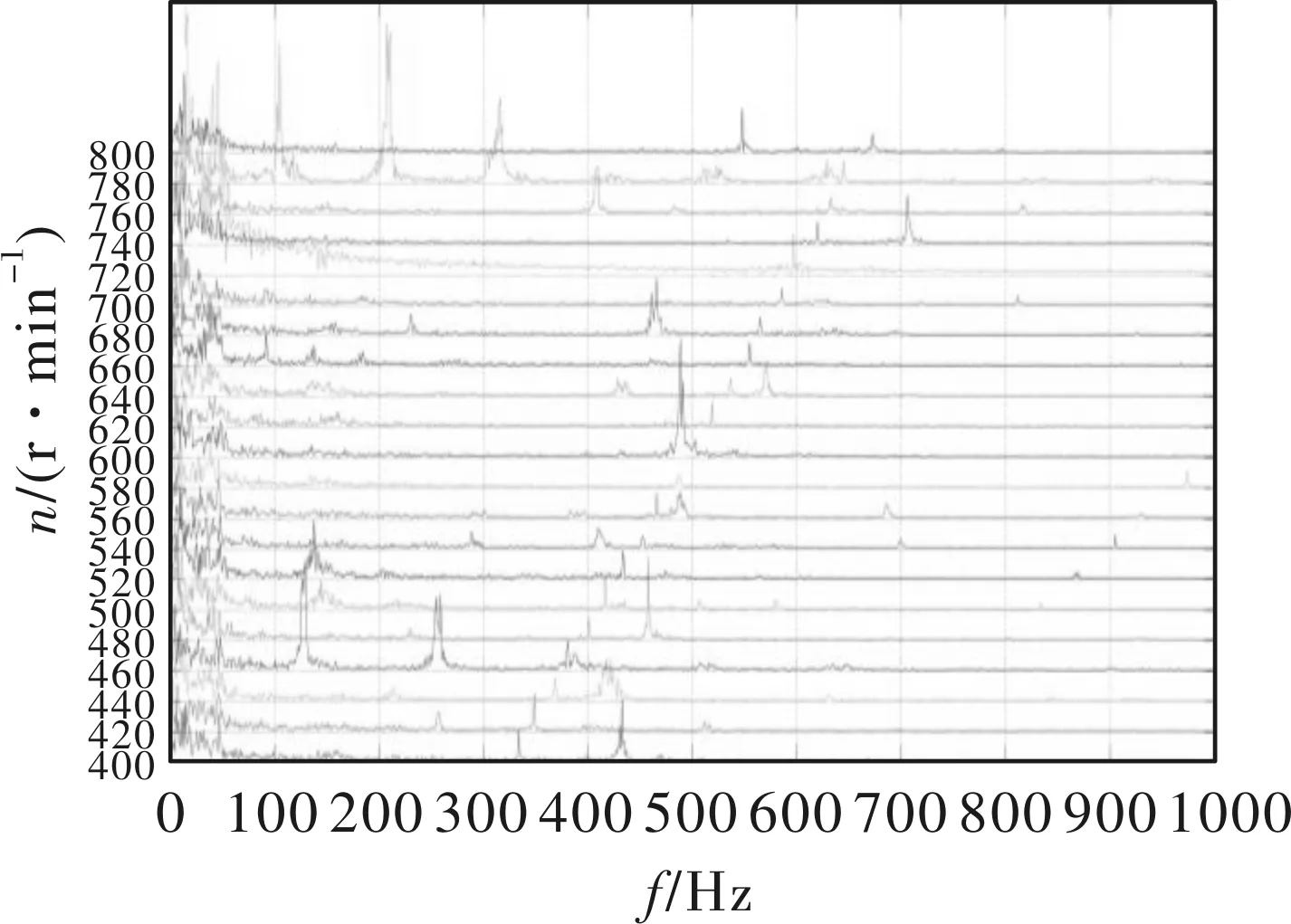
图5 低频振荡区噪音瀑布图

若电机在该区域出现强烈振动，甚至失步而无法工作，可采取多拍运行的方式，再加上一定的阻尼和干摩擦负载，电机振动的振幅可以减小，并稳定运行。

图6 谐波噪音分析

图6显示了8拍运行状态下由谐波引起的噪音信息。步进电机的驱动方式决定了定子相电流含有比较丰富的谐波成分。在这张图上，针对400 r/min的速度，可以进行以下的分析：

(1)由式(1)可以估算出由电机绕组基波电流引起的谐波电磁转矩脉动产生的噪音的基频为

在一些文献中提到四倍次谐波磁导会引起定位转矩脉动，而这是两相电机的结构导致。在作者所进行的实验中也能够看到四倍次谐波电流引起的电磁噪音比较大，并且在微步驱动中，并没有得到明显的改善，如图6至图9所示。具体的抑制该谐波电磁转矩的方法可参考文献[4]。

图7 共振频率分析

二相混合式步进电机的共振频率由电机本体结构决定，与电机的转速和驱动频率无关。本文实验中，无论电机运行在何种细分状态下，电机的固有共振点都未发生变化，且在该共振点附近由共振引起的噪音都无法得到有效的抑制，如图 7所示，电机的固有频率始终保持在15.5kHz左右。

斩波频率是指在一个通电周期内，开关管的导通与关断频率。通常驱动器采用的斩波频率在20kHz以上。斩波频率越低，电机噪音也就越明显；斩波频率越高，电机噪音相对来说就会低一些。在斩波频率噪音瀑布图中，斩波频率点附近的噪音信息会以该频率点为中心呈发散状向两边分布，如图8虚线所指[6]。本实验采用的驱动器频率约为31kHz，与瀑布图中斩波频率点相一致。

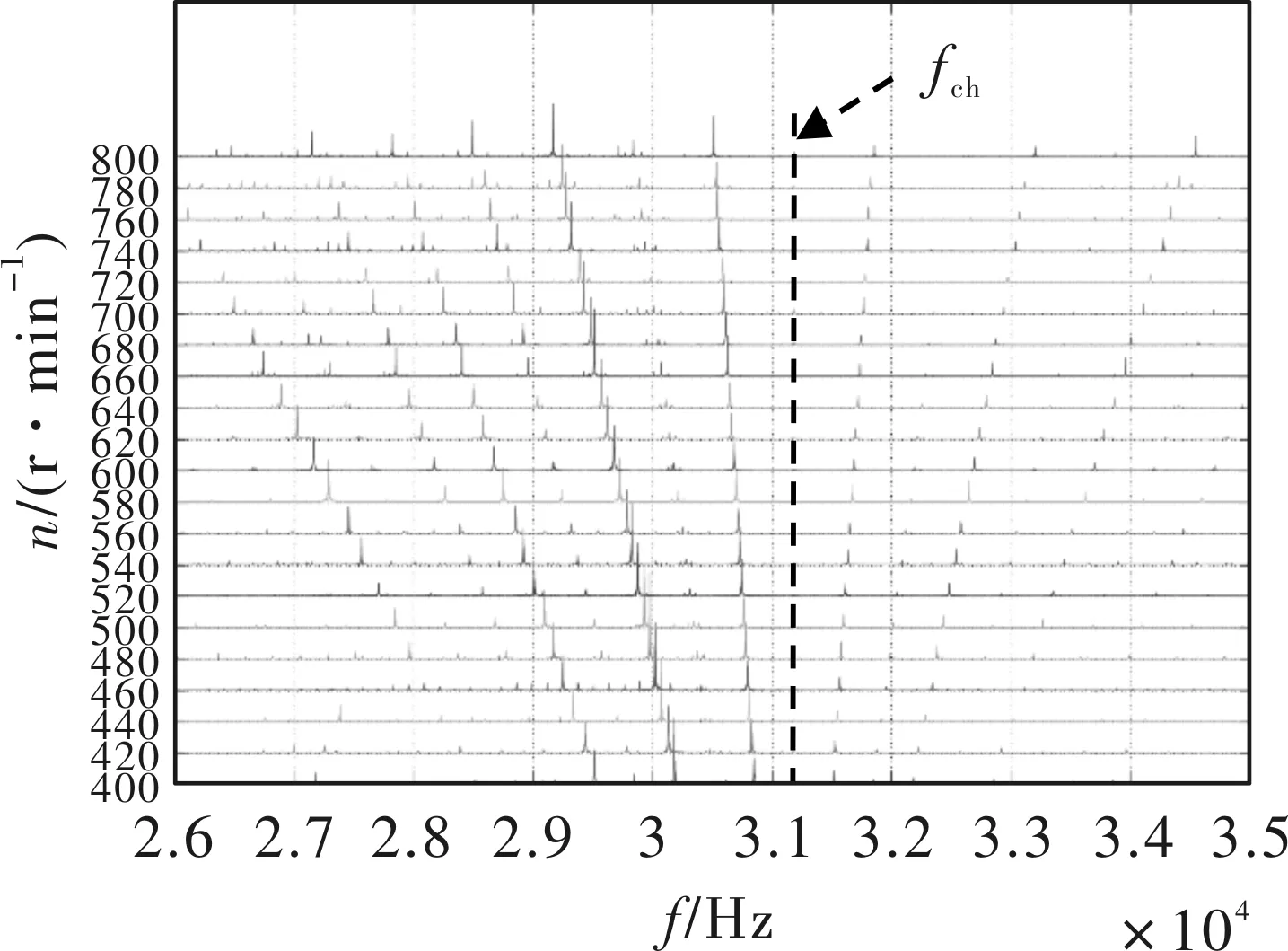
图8 斩波频率分析

图9 谐波噪音分析

如图9将32拍和64拍运行状态下的谐波瀑布图与图 6的8拍状态的作比较可以发现，随着细分数的增加，瀑布图中的声压谱振幅减小，毛刺消失，步进电机的噪音减小。同理如图10所示，通过观察32拍和64拍状态下的共振噪音瀑布图，同样可以验证驱动器的共振频率并发现电机的运行性能得到改善。

图10 共振噪音分析

3.3 电机最大转速

实验过程中，就各细分状态下二相步进电机的最高转速，如表 1所示。

表1 各细分状态下的最大转速

从表中可以看出：空载运行下，电机受制于驱动器和控制器的影响，并未达到理论最高转速。但随着细分数的增加，电机的性能得到改善，电机的最高转速得到提高。这是因为，电流趋近正弦后，电磁转矩的脉动分量减少，电机的运行较为稳定，牵入转矩得以提高，空载的最高转速也 得以提高。这也从另外一个角度验证了以上的分析，即细分能够降低电机的转矩脉动，具体表现在噪音的改变。

4 结 论

通过分析电机在不同细分驱动模式下的噪声瀑布图可以看出：由于二相混合式步进电机的细分驱动能够实现接近正弦的电流，因而在多个频域范围内能减小电机的谐波电磁转矩脉动，但在基波电流的整数倍次谐波处的噪音只能抑制而无法消除，且在电机的共振点附近由电机的本体结构引起的噪音无法通过细分得到有效抑制。通过瀑布图的分析，也可以直接了解驱动器的斩波频率及其影响。另外，细分控制可以改善步进电机的运行性能，并且能够提高电机空载运行时的最高转速。这些噪音频率点的变化能够帮助研究人员了解驱动器的性能，对深入进行高性能步进电机的驱动器的的研究提供了有效的手段。