一种改进的自适应图像量化算法*

高文斌 蒋 华 赵 成 李晓琳

北京电子科技学院，北京市 100070

引言

合成孔径雷达(SAR)具有全天候、全天时、二维分辨率高等独特优势，在监测领域中发挥着极其重要的作用。在SAR信号处理过程中，需要将SAR成像结果量化成灰度图像，目前广泛采用的是均匀量化算法，其将输入图像数据按照幅值大小均匀地划分成不同的灰度等级[1]。由于SAR图像的动态范围较大，均匀量化方式常常导致图像细节损失，并且输出的灰度图像的整体灰度往往偏暗。即使通过手动调整图像灰度等级的方式能够改变图像偏暗的问题，也容易出现整体图像灰度偏亮的情况，并且无法适用于实时图像的自动化量化处理。对于弹载、无人机载SAR系统这种需要对实时图像进行自动化控制的场合，对SAR实时图像进行自适应量化具有重要的现实意义。

1 已有图像量化算法

为了对SAR图像进行显示和目标识别，需要对图像数据进行灰度调整和量化使其变为具有一定动态范围的灰度图像。为了将SAR图像中目标的反射强度转化为灰度等级，已有文献倾向于将二者映射为线性关系，即采用均匀量化方式。其具体量化过程如下[2]：

1)寻找图像数据幅值的最大值Amax和最小值Amin；

2)确定灰度等级总数，一般为256，并以Gmin＝0作为下限，以Gmax＝255作为上限；

3)计算每个灰度等级对应的图像数据幅值间隔，即ΔA＝(Amax-Amin)＼(Gmax-Gmin)；。

4)计算每个图像数据幅值A对应的量化灰度值，即GA＝(A-Amin)/ΔA＋Gmin

上述均匀量化方法简单易行，被广泛应用于SAR图像灰度量化。然而，采用此方法进行处理后经常出现SAR图像的整体灰度级别偏低的现象，从而使得图像的对比度受到影响，造成图像的层次感和可辨识度均变差。即使通过手动调整图像增益范围，改变了图像整体的灰度级别，图像的层次感和可辨识度也无法优化。而且，在SAR信号处理过程中，对于动态范围大的图像，均匀量化会引起图像细节信息损失。

2 改进的自适应图像量化算法设计

为了解决已有图像量化算法存在的问题，本文提出一种改进的自适应SAR图像量化方法，既能够解决均匀量化方法中存在的SAR图像整体灰度级别偏高或者偏低的现象，也能解决在大动态范围区域SAR图像细节信息损失的问题。为了顺利提出针对均匀量化的改进自适应图像量化方法，本文先对SAR回波信号的性质进行分析。

2.1 SAR回波信号特性分析

已知SAR回波信号是观测场景内各个独立散射单元回波的叠加。经过SAR成像处理，每个散射体的回波可以表示为：。其中An和φn分别表示第n个散射体的回波幅度和相位。因此，SAR图像中某个像素的回波可以表示为，其中A和Φ分别为该像素的回波幅度和相位，An和φn分别是该像素内第n(n＝1，2，…，N)个散射中心对应的回波幅度和相位。将AejΦ展开得到

按照中心极限定理，当散射单元足够多时，各个独立同分布的散射单元回波之和服从高斯分布。当N足够大，且各散射中心回波的相位和振幅独立同分布，那么测量得到的某个像素的回波AejΦ的两个分量z1＝AcosΦ和z2＝AsinΦ是独立分布的高斯随机变量[3]，

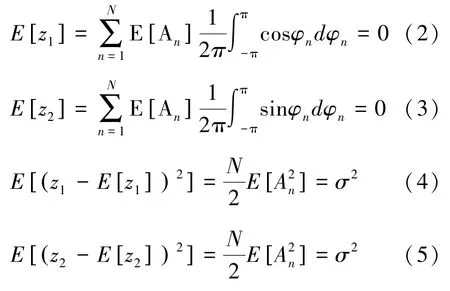
所以可以推出z1和z2的概率密度函数分别为[4]

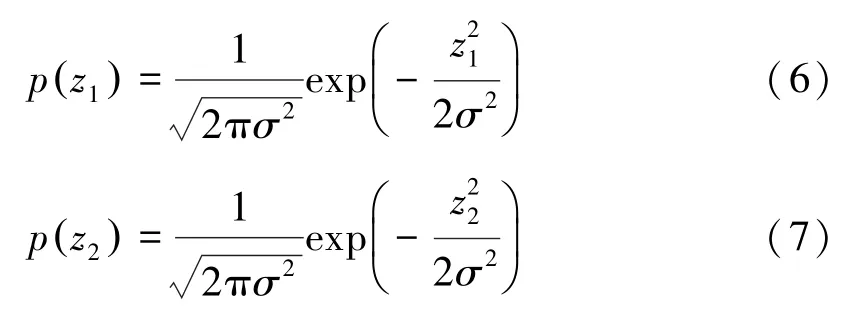
z1和z2的联合概率密度函数为

其中，σ2是z1和z2的方差，相位Φ服从[-π，π]的均匀分布，振幅服从瑞利分布，其概率密度函数为

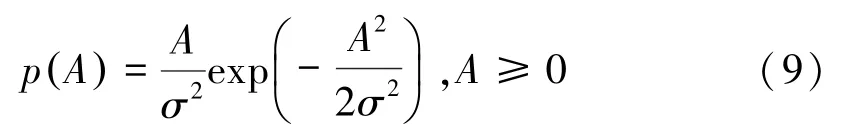
由瑞利分布的概率密度函数可以求出振幅A的均值和方差如下：

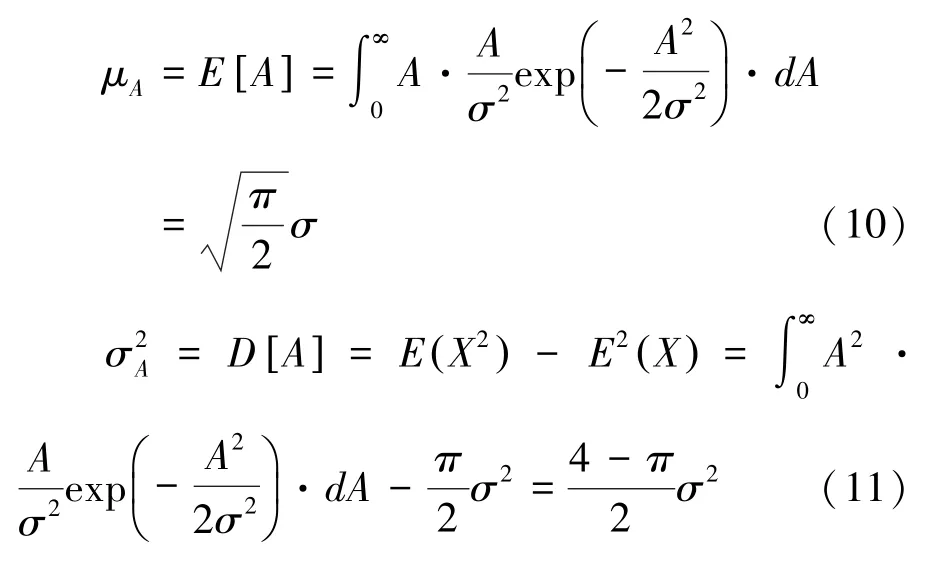
振幅 A位于区间[0，μA＋3σA]的概率可以计算为

将公式(10)和(11)带入(12)可以计算得到，标准瑞利分布中变量 A位于区间[0，μA＋3σA]的概率大于99%。也就是说，在SAR图像中，位于幅值区间[0，μA＋3σA]内的像素个数占整幅图像的99%以上。

由于地物散射特性的不同，SAR成像处理得到的图像数据仍然存在一定的非平稳性，其图像幅值的概率分布参数会随着时间的变化而发生改变[5]。同时，通过对大量实测数据进行统计分析得到，虽然有些图像像素幅值分布与标准瑞利分布可能有所偏差，但是位于幅值区间[0，μA＋3σA]内的像素个数占整幅图像的95%～99%。这对SAR图像灰度量化而言是可以接受的，因为位于区间[0，μA＋3σA]之外的像素点其亮度与图像整体亮度相差较大，为了保证图像灰度均衡，需要对该部分像素点的灰度值进行削弱。

2.2 改进的自适应图像量化算法

基于2.1节的分析，本文接下来提出一种改进的自适应SAR图像量化方法，其具体量化过程如下：

1)计算图像数据幅值的均值μA和方差；

2)确定灰度等级总数为256，并以Gmin＝0作为下限，以Gmax＝255作为上限；

3)确定图像数据幅值的范围为[0，μA＋3σA]，幅值大于μA＋3σA的像素点灰度值设为255；

4)计算每个灰度等级对应的图像数据幅值间隔，即ΔA＝(μA＋3σA)＼(Gmax-Gmin)；

5)计算每个图像数据幅值A对应的量化灰度值，即GA＝A/ΔA＋Gmin。

在实测数据处理中，计算图像数据幅值的均值μA较简单，而方差的计算相对复杂，计算量较大且需要开根号，不便于算法的硬件实现，因而不利于实时SAR图像的自适应量化。因此，需要采取更简便的方法对图像数据幅值的方差进行计算。由公式(10)可知，

然后利用公式(11)可得

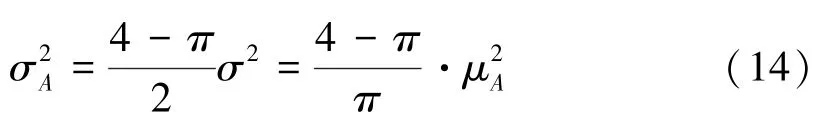
从公式(13)和(14)可知，利用瑞利分布均值与方差之间的定量关系，可以通过图像数据幅度均值μA快速计算得到图像数据幅度方差，从而可以保证实时图像的快速自适应量化。因此，改进的自适应图像量化算法流程可以用图1进行描述。

图1 改进的自适应图像量化算法流程

3 实测数据验证

采用车载SAR实测数据对本文所提算法进行验证。SAR系统参数如表1所示。

表1 系统参数

利用上述参数的车载SAR系统对上海某地进行观测并采集回波数据，共获得约40 GB原始回波数据。通过对原始回波数据进行成像处理，得到SAR图像数据。对所得图像数据进行幅值分布统计，得到如图2所示结果。从图2可知，SAR图像数据幅值确实服从瑞利分析，从而证明了上述理论分析的正确性。

图2 SAR图像数据的幅值分布

对数据处理得到的所有SAR图像数据进行自适应图像量化，均能够得到很好的图像视觉效果。接下来，本文将分平地、城区和树林等3种常见的SAR图像场景对自适应图像量化效果进行展示，并与传统均匀量化所得图像进行对比，进而验证本文所提图像量化算法的有效性。

3.1 平地

按传统均匀量化方式对平地场景图像数据进行灰度量化，得到SAR图像如图3(a)所示。从图3(a)可知，整幅图像的灰度等级偏低，导致图像内容偏暗，图像可辨识度较差。为了改善此现象，传统图像处理中往往利用经验值对均匀量化总图像数据幅度的最大值Amax进行人为调整。利用人为调整之后的最大值A′max对图像数据再次进行均匀量化，得到SAR图像如图3(b)所示。从图3(b)可知，整幅图像的灰度等级偏高，导致图像内容偏亮，图像层次感较差，并且图像细节信息丢失。经图像评估可得，图3(a)和图3(b)的图像对比度分别为5.0605和5.1635。

图3 均匀量化所得SAR图像

采用本文所提出的改进的自适应图像量化算法对同样的SAR图像数据进行灰度量化，量化所得SAR图像如图4所示。对比图4和图3(b)，特别是两图的白色虚线框部分，可以发现经过本文所提改进图像量化算法处理所得SAR图像的灰度等级适中，既保证了图像具有较好的可辨识度，又保证了图像具有较好的层次感，图像细节信息得到了很好的保留。经图像评估可得，图4的图像对比度5.1788。已知图像对比度越高，图像质量越好。因此，对于平地场景，本文所提的改进自适应图像量化算法相比传统均匀量化算法能够取得更好的图像量化效果。

图4 改进的自适应图像量化所得SAR图像

3.2 城区

采用与平地场景相同的处理流程，对城区场景图像数据进行灰度量化，得到如图5(a)、图5(b)和图6所示结果。经图像评估可得，图5(a)和图5(b)的图像对比度分别为 4.5662和4.6511，图6的图像对比度为4.6754。对比图5(a)、图5(b)和图6的对比度和视觉效果，可以发现：对于城区场景，本文所提的改进自适应图像量化算法相比传统均匀量化算法也能够取得更好的图像量化效果。

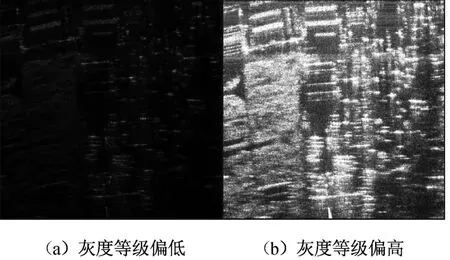
图5 均匀量化所得SAR图像

图6 改进的自适应图像量化所得SAR图像

3.3 树林

采用与平地场景相同的处理流程，对树林场景图像数据进行灰度量化，得到如图7(a)、图7(b)和图8所示结果。

图7 均匀量化所得SAR图像

经图像评估可得，图7(a)和图7(b)的图像对比度分别为3.2329和3.3051，图8的图像对比度为3.3169。对比图7(a)、图7(b)和图8的对比度和视觉效果，可以发现，对于树林场景，本文所提的改进自适应图像量化算法相比传统均匀量化算法也能够取得更好的图像量化效果。

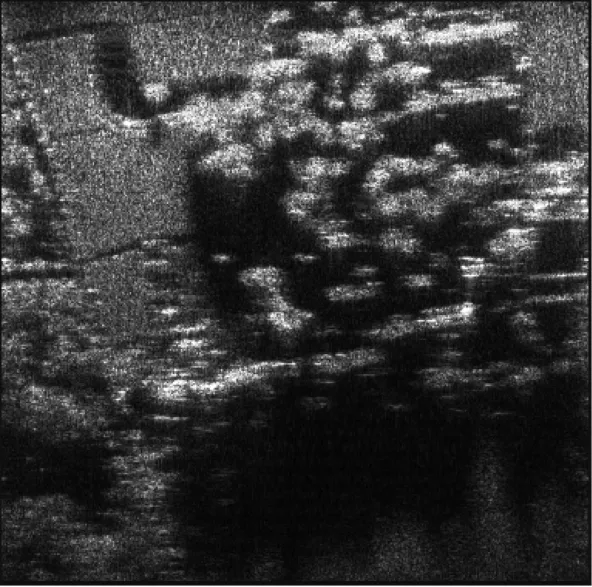
图8 改进的自适应图像量化所得SAR图像

由上述3种典型场景的图像量化结果可知，无论对于平地、城区还是树林场景，本文所提的改进自适应图像量化算法相比传统均匀量化算法都能够取得更好的图像量化效果，从而验证了本文所提算法的有效性。

4 结语

本文提出了一种改进的自适应图像量化算法。本算法根据SAR回波数据的分布特性自动计算SAR图像数据幅值的均值和方差，以此确定图像量化区间，进而计算得到图像各像素的灰度量化值。由于本算法能够自适应计算图像量化区间，并且图像幅值的均值和方差计算简单易行，因而能够适用于实时图像的快速自适应量化，具有广泛的应用前景。