解题教学重在积累解题经验

☉江苏省高邮市第一中学 潘梅耘

数学离不开解题，解题离不开解题教学，尤其到了高三，解题教学成了课堂教学的主旋律.一切活动都围绕着解题进行，教师出题、讲题，学生做题、练题.解题教学的目的到底是为了什么？当然是为了提升学生的解题能力与水平.那么，影响学生解题能力与水平提升的关键因素是什么呢？其实就是解题经验，正所谓“一盎司经验胜过一吨理论”.解题经验最直接的表现就是直觉判断，在遇到类似的问题或新的问题时能下意识地回忆或联想，并迅速作出判断，然后能够运用学过的知识灵活应对.因此，解题教学的目的并不是重复训练来得到正确的答案，而是帮助学生持续地积累解题经验.下面笔者就以一道典型例题为例，谈谈对此的做法.

一、设置思维障碍，引发经验冲突

例题已知实数x1，x2，y1，y2满足的最大值为 ______.

分析：此题看上去比较“抽象”，涉及多个参数，而且求最值问题恰恰是学生的软肋.但仔细观察，似乎发现有很多“熟悉”的元素，比如，这显然表示的是“圆的方程似乎跟“数量积”存在着某种联示的是点到直线的距离.综上所述，此题仍是立足于学生已有的解题经验，故此题的解题思路还是“有迹可循”的.

学生已有的解题经验是新的学习的基础，是学习之所以发生的中间环节，也是解题教学得以顺利实施的条件和中介.因此，在例题的选择上应该立足于学生已有的经验，例题的难度也应该遵循适当原则.题目难度不能太低，若学生套用已有的经验很容易解决，那么学生的经验就无法得到提升；如果题目难度太高，完全脱离学生的经验，那么经验的积累就是“空中楼阁”，根本无从谈起.例题应该让学生感到既“似曾相识”，有解题的想法，又让学生觉得“相对陌生”，不容易获得正确的答案.

二、联系已有经验，探索解题方向

积累解题经验需要从学生已有的经验和直观开始，让学生经历思考的过程，从中领会和感悟并形成一定的思维模式.因此，在解题教学中，教师不要急于把正确的解题思路抛给学生，来迫不及待的提炼解题思想方法，而是要联系学生已有的经验，在尊重学生想法的基础上作适当的拓展引导.

对于上述例题，学生最直观的感受就是“形”，因此，学生的解题经验就是从几何视角入手来寻找问题的突破口.

图1

由于题目中涉及两个动点A，B，无法直接从图像中看出它们的变化规律.若能把两个动点转化为一个动点，那么问题就会得到简化.

设AB的中点为M，点M到直线x+y-1=0的距离设为|MN|，则|AA1|+|BB1|=2|MN|，而|MN|≤ |OM|+|ON|，当且仅当M，O，N三点共线时，等号成立，此时|OM|+|ON|=

三、尝试多种经验，获得解题模型

一般来讲，首先想到的思路是学生最熟悉最自然的思路，这种思路通常源自于学生的第一感觉，是最先想到的经验.学生解决问题不只依赖于一种经验，很多经验是隐藏在思维深处，被最先想到的经验所遮盖.不同经验引出的解法可能有巧笨之别，但都有其存在的价值，有的时候，所谓“简单”方法是通过尝试不同的解题经验而最终得到的最佳结果.通过尝试不同的经验，学生的思维被充分地激活，从而为积累更多的经验提供宝贵的思维空间.

在上述解题中，借助了“单位圆”这一模型使抽象的问题直观化，静态的问题动态化，从而突破解题障碍.立足于学生“形”的经验，引发学生对“单位圆”展开联想，“单位圆”模型在哪块知识中用的最多呢？不就是三角函数吗？整个三角函数体系都是建立在“单位圆”模型上的，包括任意角的定义、任意角的三角函数、各种三角函数公式等等，无不依赖于“单位圆”，这也是三角函数为什么被称为“圆”函数的根本原因.于是，我们自然想到本题的第二种解题视角：函数视角.

由上述解法可知正三角形AOB在绕着顶点O旋转，可以知道最大值是在A，B运动到第三象限时取得.

通过上述解法，发现除了从“形”入手外，还可以借助“数”的工具加以解决.而且，学生发现解决问题的关键是“去绝对值”，由此就引发了从“绝对值不等式”视角来寻找解题的线索.

四、反思解题过程，内化解题经验

数学解题经验不能传递、不能通过训练获得，必须通过本人感悟，而感悟的主要形式就是反思.而解题反思的本质就是一种数学元认知体验，是伴随数学认知活动的认知体验或情感体验.在解题反思中，主体对认知经验进行自我检查和评价，比如，方法的正确与否、是否足够简便、下次碰到类似的问题是否能够想到用同样的方法加以解决，从而引发学生对解题经验的内化.

通过对以上几种解法的比较，“形”的视角不仅直观，而且只要找对方向，不需要太多的技巧就可以解决问题，而“数”的视角依赖于对“形”的理解，在运算过程中需要一定的变化技巧.因此，从“形”入手，以形助“数”是解决此类问题的一般经验，也是学生经验积累的重点.那么，此类问题到底反映了“形”的本质是什么？把这个问题搞清楚了，就有助于促进解题经验的内化.

如图2所示，此类题可以简化为这样的一类几何问题：已知△AOB是边长为1绕着O点旋转的等边三角形，点O到定直线l的A，B到定直线l的距离分别是d1，d2，求d1+d2的最大值.

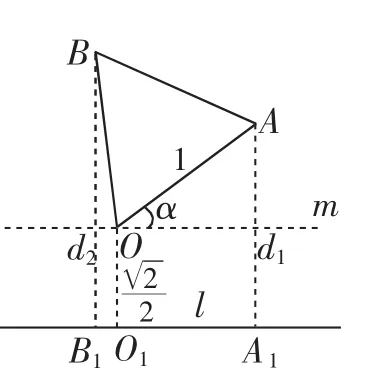
图2

设OA与水平线m所成的角为α，α决定了△AOB旋转后的位置，则

同样是从形的角度入手，但换个观察视角，引进新的参数，解题过程就得到大大的简化.凡是涉及图形的端点到直线的距离问题时都可以按照这样的思路进行解决.

数学解题教学的本质就是一个解题经验积累的过程，其中包括了“解题策略经验”“问题策略经验”以及各种“方法和技巧性经验”，但这些经验不能靠教师的传授，而是要靠学生在亲身经历中获得积累.因此，解题教学的重心应放在经验的积累上.