邻域粗糙集的随机集成属性约简

沈 林

( 莆田学院 信息工程学院， 福建 莆田 351100 )

2008年，胡清华等通过引入邻域关系，构建了邻域粗糙集模型(neighborhood rough sets，NRS)[1]，解决了Pawlak的粗糙集理论(rough sets，RS)无法处理数值型数据的问题[2].此后，许多学者对邻域粗糙集模型进行了研究[3-6].目前，NRS被广泛应用于知识发现、规则提取等领域.属性约简是去除冗余属性、获得精简知识的前提，对研究NRS具有重要作用.辨识矩阵是粗糙集属性约简的主要方法之一，但由于传统辨识矩阵仅记录样本间的辨识信息，缺少决策分布的相关信息，因此难以应用于变精度邻域粗糙集(variable precision neighborhood rough sets，VPNRS)的属性约简.文献[7]提出了一种改进的辨识矩阵，解决了变精度邻域粗糙集的属性约简问题，但该改进的辨识矩阵占用空间较大，限制了其在大规模数据上的应用.基于上述研究，本文提出一种基于随机抽样的属性约简算法，并通过对多个UCI数据集的实验，验证本文方法的可行性.

1 基本概念

1.1 邻域粗糙集和变精度邻域粗糙集模型

定义1[1]有决策系统DS=(U,C∪D,V,f)，U是非空样本集，C是条件属性，D是决策属性，f是U×(C∪D)→V的映射函数.样本xi∈U的邻域关系记为δA(xi)={xj|xj∈U,ΔA(xi,xj)≤δ}， 其中δ是邻域半径，属性集A⊆C，ΔA(xi,xj)是样本xi和xj的距离函数.

定义2[1]对于给定的集合X⊆U， 属性集A的上近似和下近似定义为：

(1)

上下近似是粗糙集中的重要的概念之一，是用于分析精确、模糊知识的重要工具.定义2要求处理的样本必须是精确的，但因其抗噪音能力差，所以在实践中往往会引入精度β(0≤β≤0.5)， 即将粗糙集变为变精度邻域粗糙集.变精度邻域粗糙集的上下近似定义为：

定义3[1]当有非空样本集X⊆U， 则X关于属性A的β上、下近似可以描述为：

(2)

1.2 基于依赖度的属性约简

基于依赖度属性约简的基本思想是通过计算依赖度，寻找到可以保持正域不变的属性约简(下面记作Dependence算法).

定义4[2]决策系统的近似邻域依赖为

r(DS)=|POS(DS)|/|U|.

(3)

其中POS(DS)= ∪CδYj，Yj⊆U/D是决策属性D对样本U的划分，CδYj为决策类Yj在条件属性C的δ邻域关系下的下近似，POS(DS)是决策类下近似的并集.

定义5[2]对于属性集A⊂C， 当rA(DS,β)=r(DS,β)时，则认为属性A是C的一个约简.

1.3 基于辨识矩阵的变精度邻域粗糙集属性约简

因传统的辨识矩阵不能直接应用于VPNRS，文献[8]定义了一种新的辨识矩阵，如公式(4)所示：

(4)

该辨识矩阵的每行是一个样本对，每列对应一个属性， 数字0表示样本对不是邻域关系， 数字1表示样本对是邻域关系且决策属性相同， 数字2表示样本对是邻域关系但决策属性不同.在每一轮属性选择中，选择数字值2与数字值1比值最低的属性.由于该方法无需反复计算各样本的邻域和精度，因此降低了时间复杂度.为了避免对某个决策类过度拟合，文献[7]的算法在约简过程中还检验了下近似分布不变.

定义6[7]决策系统的下近似分布的定义为：

DP(DS,β)={Cβ δY1,Cβ δY2,…,Cβ δYn},

(5)

其中Cβ δYj为决策类Yj在条件属性C的δ邻域关系下的β下近似.

文献[7]中的改进辨识矩阵算法(下面称为BMLNRS算法)的具体流程如下：

a)按照式(3)计算样本集的邻域辨识矩阵.

b)计算全属性C下的下近似分布.

c)找出精度最高的属性{ai|min(|M(ij)ai=2|/(|M(ij)ai=1|+m))}，m是元素个数，并将该属性放入已选属性队列，然后执行步骤e).

d)将剩余属性依次和已选属性队列做位与运算，将精度最高的属性加入已选属性队列.若有多个剩余属性可以得到最高精度，则选择数值1最多的剩余属性.

e)检查下近似分布是否和b)一致，如果是则输出已选属性队列并结束算法，如果不是则重复d)、e)步骤，直到满足条件.

2 基于随机抽样的集成属性约简

为了解决BMLNRS算法空间占用过高的问题，本文通过随机抽样获得多个不同的小规模样本，然后利用BMLNRS算法分别进行约简.在获得多个有一定差异的属性子集后，计算每个属性子集的权重，并选取最好的n个属性子集在之前抽取的小规模样本上进行测试，以此选出精度最好的属性子集.为了进一步减少空间占用，将文献[7]中按字节存储矩阵元素的方法，改为按二进制位存储.整个算法如图1所示.

图1 本文算法的流程图

在计算属性子集的权重时，若在多组不同的属性子集中，某属性出现的次数多，则表示其分辨决策类的能力强.权重的计算公式如下：

(6)

其中ωCi表示属性Ci的权重，ωSi表示属性子集Si的权重.

3 实验结果

所有实验均在Windows7环境下完成.首先在Matlab下编写代码，以此获得属性约简的子集，然后使用WEKA自带的算法验证精度.本文从UCI数据集中选择5个大规模数据集来验证本文算法的效果，所有数据集均为数值型数据，如表1所示.

表1 数据集参数

3.1 各抽样比例的空间占用和时间消耗

不同抽样比例对辨识矩阵空间占用的影响如表2所示.从表2可以看出，随着抽样比例的降低，辨识矩阵的占用空间迅速减少.在30%抽样比例时，占用空间为全集的2%～3%；在10%抽样比例时，占用空间只有全集的0.25%～0.35%.这说明，随机小规模样本子集可以显著减少辨识矩阵的占用空间.

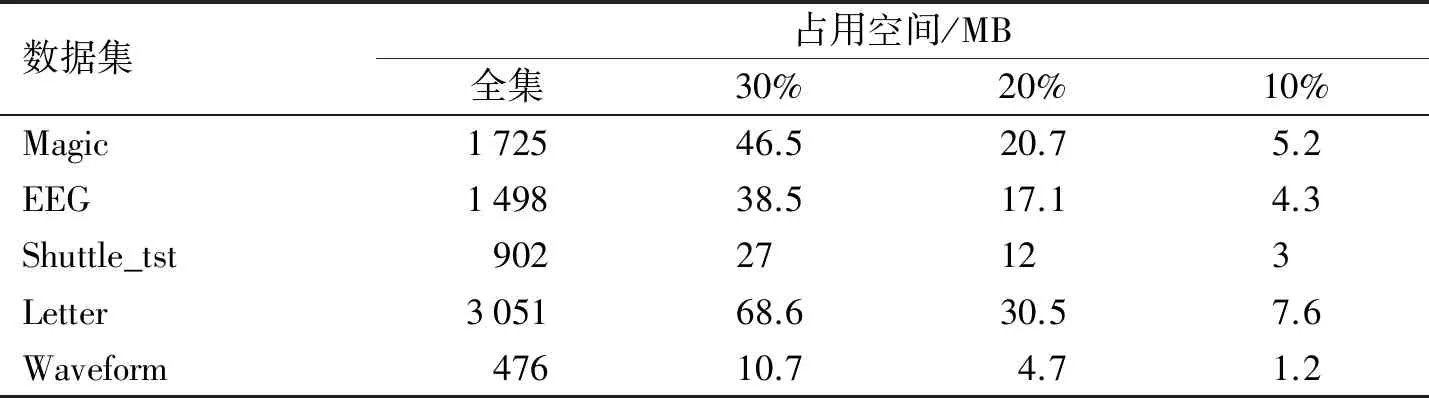
表2 各抽样比例的空间占用

为了避免算法运行时间超过全集时的运行时间，将本文算法的运行时间与全集时的Dependence算法、BMLNRS算法进行比较，结果如表3所示.随机抽取本文算法的15个样本子集(按30%、20%、10%比例分别随机抽取5次)进行运行.从表3可以看出，采用15组随机子集进行属性约简，其运行总时间明显少于BMLNRS算法和基于依赖度的算法.这说明，通过控制随机抽样的次数，可以使属性约简的时间消耗不超过全集下属性约简的时间.

表3 3种算法的时间消耗

3.2 各抽样比例和邻域半径下的稳定性

3.2.1各抽样比例对约简子集的属性个数的影响 表4和表5给出了不同抽样比例对约简后属性个数的影响.由表4可知，在0.5σ时，除Waveform外，其他数据集在各抽样比例下其约简后的属性个数与全集基本相当，即并不随抽样比例的变化而发生显著变化.但在0.3σ时(表5)，各数据集约简后的属性个数均随抽样比例的降低而减少.

表4 0.5σ邻域半径下约简后的属性个数

表5 0.3σ邻域半径下约简后的属性个数

3.2.2各抽样比例约简结果的相似度 为了进一步了解随机抽样和邻域半径对约简后属性子集的影响，将本文算法的15个随机样本子集分别按照0.3σ、0.4σ、0.5σ、0.6σ的邻域半径进行属性约简，并分别计算这些结果与全集约简结果的相似度，然后将相似度按照样本抽样比例分组并求平均值，结果如图2所示.相似度计算采用谷元距离度量法[8]：

(7)

公式中，DT的取值范围为[0，1]，取值越大，说明两个属性子集的相似度越高；取值为0时表示完全不同，为1时表示完全相同.

从图2可以看出，相似度的变化与抽样比例、邻域半径的变化没有相关性.其中，Waveform数据集的相似度低于其他数据集，这是因为Waveform数据集中有40个属性，而每个抽样比例仅随机抽取5个样本，所以相似度偏低.

图3 各抽样比例的精度

3.2.3各抽样比例的约简精度 按30%、20%、10%比例随机抽样(每个比例各抽样5次)测试各抽样比例对精度的影响.测试时，δ取0.5σ，β取0.5.约简后，用3NN、SimpleCart、SMO、Bagging、JRip、RandomForest算法计算每组的平均精度，结果如图3所示.由图3可以看出，在30%和20%的抽样比例下，除了Letter数据集，其他随机子集的精度都略高于全集.在抽样比例为10%时，随机子集的精度普遍较低，其原因是在该抽样比例下，样本子集的信息量丢失较多.

3.3 不同算法的约简效果

为了评价本文算法的分类精度，将本文算法得到的属性子集的分类精度与Dependence算法、BMLNRS算法进行对比.BMLNRS算法和本文算法的δ取0.5σ，β取0.5，Dependence算法则采用分类精度最好的结果.用3NN、SimpleCart、SMO、Bagging、JRip、RandomForest算法计算每个属性子集的精度并取平均值，结果如表6所示.

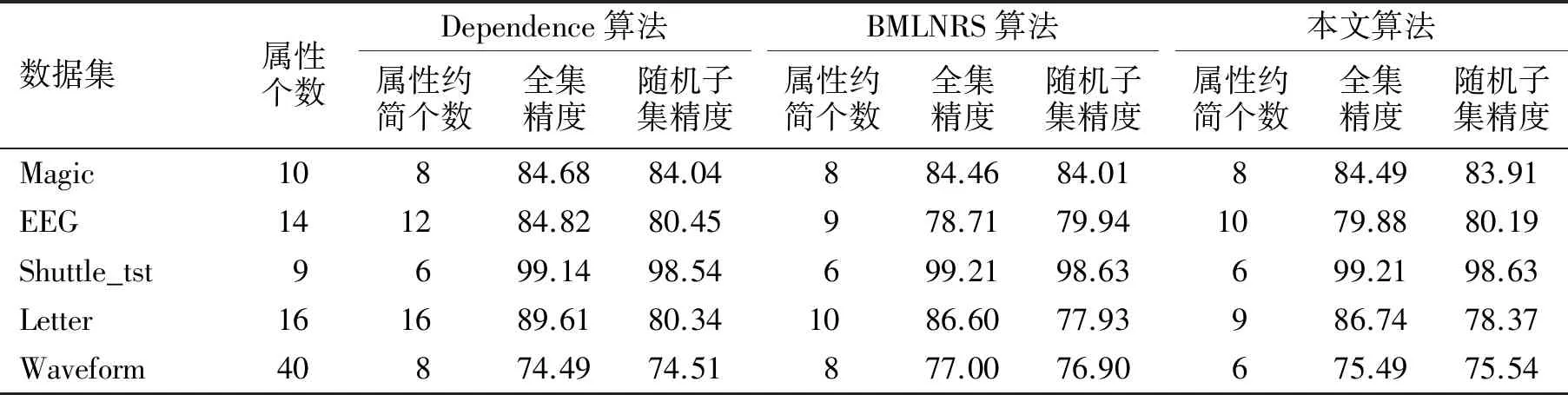
表6 3种算法的属性约简精度

从表6可以看出，本文算法的分类精度和BMLNRS算法基本相当.Dependence算法在EEG和Letter数据集上的精度优于本文算法，这是由于在这两个数据集上，Dependence算法约简后的属性个数多于本文算法，即保留的信息量多于本文算法.

4 结论

UCI数据集实验证明，本文提出的基于多次随机抽样的集成属性约简算法的空间占用比BMLNRS算法可减少2～3个数量级，且其约简精度和BMLNRS算法相当，所以本文方法在处理大规模数据时，具有更大的优势.本文在生成约简子集时，仅考虑了一种属性评价标准，该评价标准可能会更偏好个别属性，因此今后将考虑综合多种评价标准，以进一步提高本文方法的鲁棒性.