一类具有非线性发生率和治愈率的SEIRS模型研究

高雪丽, 王 辉, 胡志兴

(北京科技大学 数理学院,北京 00083)

引 言

传染病是危害人类身体健康的重要疾病。在控制和消除传染病过程中,治疗是预防和控制各种传染病传播的重要方法。在经典的流行模型中,被认为治愈率与感染个体的数量成正比[1]。在一些疾病挑战了正常公共卫生系统和能力之后,研究人员开始从建模和分析的角度来考虑医疗保健系统的能力[2]。Wang和Ruan认为,在一个社区中,治疗疾病的能力是恒定的[3]。Wang提出了以下分段函数[4]

(1)

在SEIRS模型中,其中k是治愈率,这意味着当治疗能力还没有达到极限时,治疗能力是与感染者的数量成比例的,否则将采用治疗能力的极限值常数形式作为治疗函数。治愈函数(1)已经在一些文献中得到了应用[5-7],其他的治愈函数也被提出,并应用在许多文献中,例如饱和治愈率T(I)=rI/(1+μI),r>0,μ≥0[8-10]。

本文主要考虑了在有限资源的情况下公共卫生系统对病人的治疗能力,这可能发生在很大一部分情况下,比如患者人数较多,但医疗设施不足、床位数量有限等,应用了分段函数(1)作为治愈函数。又在模型中应用了饱和发生率[11],并考虑了恢复者再次丧失免疫变为易感者[9]。建立了饱和发生率和分段函数治愈率的SEIRS传染病模型。

1 传染病模型的建立

建立以下易感者—潜伏者—病染者—恢复者—易感者(susceptible-exposure-infected-recovery-susceptible)传染病模型:

(2)

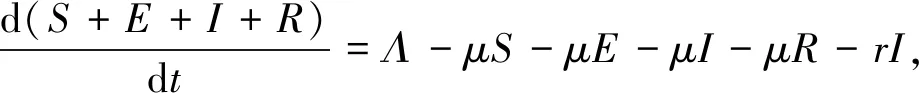
2 平衡点的存在性

设系统(2)的正平衡点为I*,当0

(3)

当I*>I0时,使系统(2)右边得零,可得

(4)

2.1 地方病平衡点P*(S*,E*,I*,R*)的存在性

由系统(3)可得基本再生数

(5)

经计算可得当R0>1时,系统(3)有唯一的地方病平衡点P*(S*,E*,I*,R*),其中

(6)

(7)

同时式(6)中的I*必须满足I*I0,即可得

(8)

2.2 地方病平衡点P1(S1,E1,I1,R1),P2(S2,E2,I2,R2)的存在性

由系统(4)可以得到I*必须满足如下方程

b0(I*)2+b1I*+b2=0,

(9)

其中

b0=(ψ+μ)(μ+σ)(β+bμ)(μ+r+θ)-βψσθ,
b1=(ψ+μ)[(μ+σ)μ(μ+r+θ)-βσΛ]+uμ[b(ψ+μ)(μ+σ)+(μ+σ+ψ)β],
b2=(ψ+μ)(μ+σ)uμ。

(10)

(11)

由式(10)可以得到

(12)

其中

a1=b(ψ+μ)(μ+σ)+(μ+σ+ψ)β;

a2=(ψ+μ)[βσΛ-(μ+σ)μ(μ+r+θ)][b(ψ+μ)(μ+σ)+(μ+σ+ψ)β]>0;

a3=[(ψ+μ)(μ+σ)(β+bμ)(μ+r+θ)-βψσθ](ψ+μ)(μ+σ)>0;

a4=(ψ+μ)[(μ+σ)μ(μ+r+θ)-βσΛ]。

由式(12)的二次方程便可以得判别式

(13)

或

(14)

当(σ+μ)μ(μ+r+θ)<βσΛ时,可得u0

因此当且仅当(σ+μ)μ(μ+r+θ)<βσΛ,uu0时b1<0,Δ≥0。

假设b1<0,Δ≥0,则式(9)有两个正根I1,I2,

(15)

则

如果Ij>I0,则Pj(j=1,2)是系统(2)的一个地方病平衡点。

u

(16)

其中

l1=2[(ψ+μ)(μ+σ)(β+bμ)(r+μ+σ)-βψσθ]+kμ[b(ψ+μ)(μ+σ)+(μ+σ+ψ)β]。

也等价于(2b0I0+b1)2-Δ>0,经过计算可以得出

于是可得

(1)如果(σ+μ)μ(μ+r+θ)<βσΛ(σ+μ)μ(μ+r+θ+k)则可以得到(b1+2b0I0)2-Δ>0。

(2)如果βσΛ>(σ+μ)μ(μ+r+θ+k),则R0>1;(b1+2b0I0)2-Δ>0等价于u>u2。

因此可得当且仅当

1)u

2)uu2,uu0,R0>1时,I1>I0。

其中k1=μ(μ+σ)(μ+r+θ);k2=(ψ+μ)(μ+σ)(μb+β);

l2={2[k2(r+μ+θ)-βψσθ]+kμ[b(ψ+μ)(μ+σ)+(μ+σ+ψ)β]}(μ+σ)μ(k+μ+r+θ)。

同理可以计算在I2存在时,满足I2>I0的条件,可以用反证法。

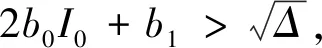
我们即得到当I2>I0时,当且仅当

1)u

2)uu0,u1。

归纳总结以上讨论分析,有文献[7]中类似的结论。

定理2.1当(σ+μ)μ(μ+r+θ)≥βσΛ或u>u0时,系统(2)的地方性平衡点P1,P2都不存在,我们假设(σ+μ)μ(μ+r+θ)<βσΛ,uu0,于是有下面结论。

1)当R01,u

推论2.2

1)当R0<1,(σ+μ)μ(μ+r+θ)<βσΛ,且umin(u0,u1)时,地方病对平衡点P1,P2存在,则系统(2)关于地方病平衡点存在一个后向分支。

定理2.3

2)当且仅当R0>1,u≥u2,系统(2)的地方病平衡点P*(S*,E*,I*,R*)存在进一步当u>u0或u1

证明由式(14)得u>u0意味着Δ<0,则此时P1,P2都不存在。当u1

3 平衡点的稳定性

由文献[7]的定理3.1的证明过程可证系统(2)的无病平衡点P0局部渐近稳定性和全局渐近稳定性。

定理3.1当基本再生数R0<1时,无病平衡点P0局部渐近稳定;当R0>1时,无病平衡点P0不稳定;进一步,当R0<1,u>u0时,P0为唯一的平衡点。

证明无病平衡点P0处的雅克比(Jacobian)矩阵为

(17)

特征方程为

(λ+μ)(λ+μ+ψ)[(λ+μ+σ)(λ+k+μ+r+θ)-βσΛ/μ]=0

λ1=-μ<0,λ2=-(μ+ψ)<0,

λ3+λ4=-(2μ+σ+r+θ+k)<0,λ3λ4=(μ+σ)(k+μ+r+θ)(1-R0)。

当R0<1时,λ3+λ4<0,λ3λ4>0时可得特征根都为负值,即无病平衡点P0是局部渐近稳定;当R0>1时,λ3+λ4<0,λ3λ4<0,即λ3,λ4异号,特征根存在正值,便得无病平衡点P0是不稳定。

推论3.2当R0<1时,地方病平衡点P*不存在;若u>u0,则地方病平衡点P1,P2也不存在；则R0<1时无病平衡点P0是系统(2)的唯一的平衡点。

定理3.3如果系统(2)的地方病平衡点P*存在,则P*是局部渐近稳定的。

证明地方病平衡点P*处的雅克比(Jacobian)矩阵为

可得特征方程为

λ4+A1λ3+A2λ2+A3λ+A4=0。

其中

可得Ai>0(i=1,2,3,4),

由Hurwitz判据得特征方程的所有根都具有负实部,所以当R0>1,u≥u2,地方病平衡点P*是局部渐近稳定的。

由文献[7]的定理3.4的证明方法可证得地方病平衡点P1是不稳定的。

定理3.4如果系统(2)的地方病平衡点P1存在,则P1是不稳定的

证明地方病平衡点P1(S1,E1,I1,R1)处的雅克比(Jacobian)矩阵为

便可得

所以可得特征方程的根是异号的,一定有正根存在,由Hurwitz判据得地方病平衡点P1是不稳定的。

由文献[8]的命题2的证明方法可证系统(2)的地方病平衡点P2在一定条件下是局部渐近稳定的。

定理3.5如果系统(2)的地方病平衡点P2存在,则P2是局部渐近稳定的。

证明地方病平衡点P2(S2,E2,I2,R2)处的雅克比(Jacobian)矩阵为

可得特征方程为

λ4+d1λ3+d2λ2+d3λ+d4=0,

令

d1=μ+x1+x3+x4+x5;

d2=(μ+x1)(x3+x4)+x3x4+(μ+x1+x3+x4)x5-σx2;

d3=[(μ+x1)(x3+x4)+x3x4-σx2]x5+(μ+x1)x3x4-σx2(x5+μ);

d4=-ψσθx1+(μ+x1)x3x4x5-σx2μx5。

令

m1=μ+x1+x3+x4;m2=(μ+x1)(x3+x4)+x3x4;

m3=(μ+x1)x3x4;m4=-ψσθx1。

可得

Δ1=d1=m1+x5>0,

=(μ+x1+x3+x4+x5)](μ+x1)(x3+x4)+x3x4+(μ+x1+x3+x4)x5-σx2]

-[(μ+x1)(x3+x4)+x3x4-σx2]x5-(μ+x1)x3x4+σx2μ>0,

=(m1-μ)(μ+x5)(σx2)2+{(μ-m1+x5)(m2x5+m3)-(m1+x5)(m2+m1x5)x5-

m3](m2x5+m3)-(m1+x5)2(m3x5+m4),

Δ4=d4Δ3。

由Hurwitz判据得只要Δ3的符号就可判定地方性平衡点P2的局部渐近稳定性。记

σx2=y;

n1=(m1-μ)(μ+x5)

n2=(μ-m1+x5)(m2x5+m3)-(m1+x5)(m2+m1x5)x5-

n3=[(m1+x5)(m2+m1x5)-m2x5-m3](m2x5+m3)-(m1+x5)2(m3x5+m4),

便可得

Δ3=n1y2+n2y2+n3,

显然n1>0,n3>0。则得到P2的局部渐近稳定性的充分性条件，其可以看作是以y为变量的二次函数,显然m1>0,则得到Δ3>0的充分条件,也就得到地方病平衡点P2(S2,E2,I2,R2)的局部渐近稳定的充分条件。

(1)当Δ>0，如果yy2,则地方性平衡点P2是局部渐近稳定的。

(3)当Δ<0，对于任意的实数y,地方性平衡点P2是局部渐近稳定的,其中

4 数值模拟

这一部分将选取一系列的参数通过MATLAB数值模拟画出相应的图形,验证本文的结论,以便更直观地得到平衡点的稳定性。

对于系统(2),选取参数β=0.05,μ=0.03,ψ=0.3,b=0.1,σ=0.15,r=0.3,θ=1,Λ=3,k=3.5。通过计算可得R0=0.8627<1,u0=1.2690,u1=2.5210,即为定理2.1的情况1。如图2所示会出现一个后向分支,图中的一条直线表示无病平衡点P0,既当0

对于系统(2),选取参数β=0.05,μ=0.03,ψ=0.3,b=0.1,σ=0.15,r=0.3,θ=0.8,Λ=5.5,k=3.5。通过计算可得R0=0.8627<1,u0=1.2690,u1=2.5210,如图2所示系统(2)会出现一个后向分支。选择I0=0.29,u=1

5 结 论