非对称结构的实频率的高阶灵敏度分析

张 淼，于 澜

(长春工程学院理学院，长春 130012)

灵敏度分析首先要面对的是无阻尼系统和阻尼系统的分类问题，其次要面对的是对称和非对称系统的分类问题，再者还要考虑单频和重频系统的分类问题。灵敏度分析算法研究的趋势表明，目前较为活跃的几种方法是：1)模态法[1-3]；2)代数法[4-5]；3)直接法[6-7]；4)迭代法[8-9]。前两类方法为精确算法，后两类方法多数为近似算法。对无阻尼问题，Fox和Kapoor[1]首先推导出了对称无阻尼特征问题灵敏度的模态法表达式，Plaut和Huseyin[10]，Garg[11]，Rudisill[12]，Rudisill和Chu[13]研究了针对非对称无阻尼系统的特征对导数的模态法，文献[14-16]提出了几种修正模态算法。Nelson[17]提出了有效计算特征向量导数的直接法，而张德文等[18]也提出了直接扰动技术等直接法，Friswell[19]扩展了Nelson的方法来计算特征解的二阶及高阶导数。1997年Lee和Jung[20-21]提出了一种针对对称无阻尼系统的代数法，通过解一个具有对称系数矩阵的代数方程组来计算特征解的导数，既可应用于单特征系统，也可应用于重特征系统。目前的研究显示，灵敏度分析还要面临一些新的复杂问题，例如，是否存在标号现象[22]，是否存在亏损问题[23]，是否存在特征向量的正交性退化[24-25]现象等等。

在灵敏度分析中，特征向量之间的正交化是振动系统的固有属性，它是对振动方程及其衍生而来的方程进行解耦的基础条件，没有正交化作为方程解耦或矩阵对角化的基石，则规范化的意义不大。而当正交化属性已经存在的情况下，规范化则显得更为灵活和具有个性，因为不同的需要而使用不同的规范化条件是目前各种灵敏度算法向前发展的动力之一。前文提到有关模态法的实频率的二阶灵敏度算法公式，使用的均是实模态关于质量的加权正交性作为基础[2]，本文则采用了一种与之不同的正交规范化方法，从而提出了实现非对称系统的灵敏度分析的新的模态法。数值算例说明了本文算法的精确性、简洁性和实用性。

1 实模态参数

对N自由度的线性离散振动系统的运动方程为：

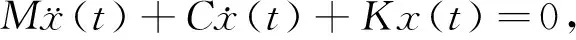
(1)

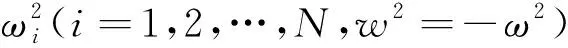
(K+λiM)φi=0。

(2)

实际上方程(2)是关于矩阵M和K的广义特征矩阵方程，称λi与φi(i=1，2，…，N)为实模态参数。

2 实模态参数的规范正交化

如果系统的性质矩阵M，C和K具有对称性，称为对称系统，否则称为非对称系统。对方程式(2)来说，每阶特征值λi都是唯一的，但每阶特征值所对应的特征向量φi却有无穷多个，因此，规定广义特征矩阵方程输出的均是满足下面条件

φiTφi=1(i=1，2，…，N)，

(3)

的特征向量，这样就保证了特征向量的唯一性。

对对称系统来说，可以证明不同实频率所对应的实模态是关于质量和刚度阵加权正交的，即

因此，可以采取如下规范化方法：首先规范化每个振型，规范化后的振型向量在应用中常称为无阻尼正则固有振型。设每个正则化系数为ai，即

记aiφi=ui，则U=[u1，…，uN]为无阻尼正则固有振型矩阵，即有

UTMU=E，UTKU=diag(-λ1，…，-λN)。

(4)

但如果系统为非对称系统，无法证明不同实频率所对应的实模态是关于质量和刚度阵加权正交，则需引入新的向量来实现类似式(4)的规范正交化。先将方程(2)转化为等价的一般特征问题

λiφi=-M-1Kφi。

令D=-M-1K，则上式写成

λiφi=Dφi，

(5)

φi(下文中也称为矩阵D的右特征向量)并不能对角化D，因为D一般为非对称矩阵，因此需引入左特征向量。

定义1 对向量ψk∈RN，如果有

(6)

则称ψk为矩阵D的左特征向量。

对式(6)右乘φi，对式(5)左乘ψkT，然后相减，显然对于λk≠λi，有

(7)

将式(6)右乘φi，并由式(7)可知

上式说明，对不同的实频率，矩阵D的左、右特征向量不仅满足正交性，而且满足关于D的加权正交性。

下面适当规范化这些左特征向量，调整ψk(k=1，2，…，N)的各维分量比例，使之满足

(8)

记左、右特征向量矩阵分别为Ψ=[ψ1，…，ψN]和Φ=[φ1，…，φN]，那么左、右特征向量矩阵满足规范正交条件为

(9)

(10)

注意此时式(10)中的φ1，…，φN仍为满足式(3)的方程(2)的原始输出模态，因为式(8)的规范化过程只调整了左特征向量，所以称为单侧规范化。

3 非对称系统实频率的一、二阶灵敏度算法

3.1 实频率的一阶灵敏度算法

假设系统(1)可以被一系列m个设计参数g=(g1，g2，…，gm)T所描述，称g为设计向量，则M，C和K都是关于g的函数。当系统发生变化时，设计向量g发生扰动，记为Δg=(Δg1，Δg2，…，Δgm)T，其中Δgj(j=1，…，m)是第j个设计参数的扰动量。在设计参数产生扰动时，系统的实模态参数也会随之发生变化，这种变化用灵敏度来反映最为直观。由于泰勒展开式的缘故，我们需要讨论实频率对设计参数的灵敏度及实模态对设计参数的灵敏度。

定义2 实模态向量φi关于第j个设计参数gj的一阶灵敏度为

定义3 实频率λi关于第j个设计参数gj的一阶灵敏度为

对非对称单频系统来说，由于所有实频率均不相同，因此它们所对应的实模态向量φk(k=1，2，…，N)线性无关，可作为广义特征空间的基底，也可作为N维向量空间的基底，因此N维向量φi，j(j=1，2，…，m)一定可在N维向量空间内表示为基底的某一线性组合

(11)

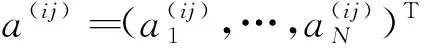
D，jφi+Dφi，j=λi，jφi+λiφi，j，

那么

(D-λiE)φi，j=λi，jφi-D，jφi，

(12)

把式(11)代入式(12)，可得一阶灵敏度系数的控制方程

(D-λiE)Φa(ij)=λi，jφi-D，jφi。

(13)

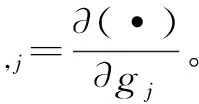
(14)

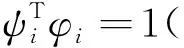
(15)

3.2 实模态的一阶灵敏度算法

由于计算实频率的二阶灵敏度时需用到实模态的一阶灵敏度，因此，先讨论实模态的一阶灵敏度算法。在一阶灵敏度系数的控制方程组(14)中除了第i个方程外都可解得N-1个一阶灵敏度系数为

即

(16)

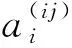
将式(11)代入上式得

用矩阵的列分块形式改写上式得

即

把规范化条件φiTφi=1代入上式可得

即

(17)

这样就得到了全部一阶灵敏度系数。将式(16)和式(17)代入式(11)可得某个确定的实模态φi的一阶灵敏度。

3.3 实频率的二阶灵敏度算法

由引言中指出求实频率的灵敏度，往往都伴随于求模态或状态向量的灵敏度的过程中，为了求实频率的二阶灵敏度，我们展开求实模态的二阶灵敏度的过程。

定义4 实模态向量φi关于先是第j个设计参数gj然后是第l个设计参数gl的二阶灵敏度为

定义5 实频率λi关于先是第j个设计参数gj然后是第l个设计参数gl的二阶灵敏度为

对非对称单频系统来说，实频率所对应的实模态向量φk(k=1，…，N)虽然不能具有如式(4)般的正交规范化关系，但却能保证无关性，可作为N维空间的基底，因此N维向量φi，jl(j，l=1，2，…，m)一定可在N维向量空间内展开为基底的某一线性组合形式，即

(18)

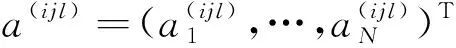
(D-λiE)，jφi+(D-λiE)φi，j=0，

然后是对第l个设计参数gl求二阶导数得(D-λiE)，jlφi+(D-λiE)，jφi，l+(D-λiE)，lφi，j+(D-λiE)φi，jl=0，

整理得

(D-λiE)φi，jl=(λiE-D)，jlφi+(λiE-D)，jφi，l+(λiE-D)，lφi，j。

将式(18)代入上式得二阶灵敏度系数的控制方程

(D-λiE)Φa(ijl)=(λiE-D)，jlφi+(λiE-D)，jφi，l+(λiE-D)，lφi，j。

(19)

将式(19)左乘ΨT，并根据规范正交关系(9)和式(10)得二阶灵敏度系数控制方程的解耦形式为

(20)

即

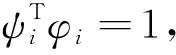
(21)

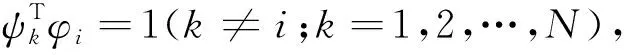
(22)

4 数值算例

设p∈R，某机翼振动模型的质量、阻尼和刚度矩阵分别是

这是一个非对称系统，本文取p作为设计参数，为了更好地展示算法的可行性，在求二阶灵敏度时，仍视p为设计参数，那么设计参数向量为g=(p，p)T，设计参数扰动量为Δg=(Δp，Δp)T。

首先将p从0.25变化至1.05，利用式(5)每隔0.1作为节点采样系统实频率λ1和λ2的数据，并利用三次样条插值绘制这些实频率的拟合曲线图，如图1。

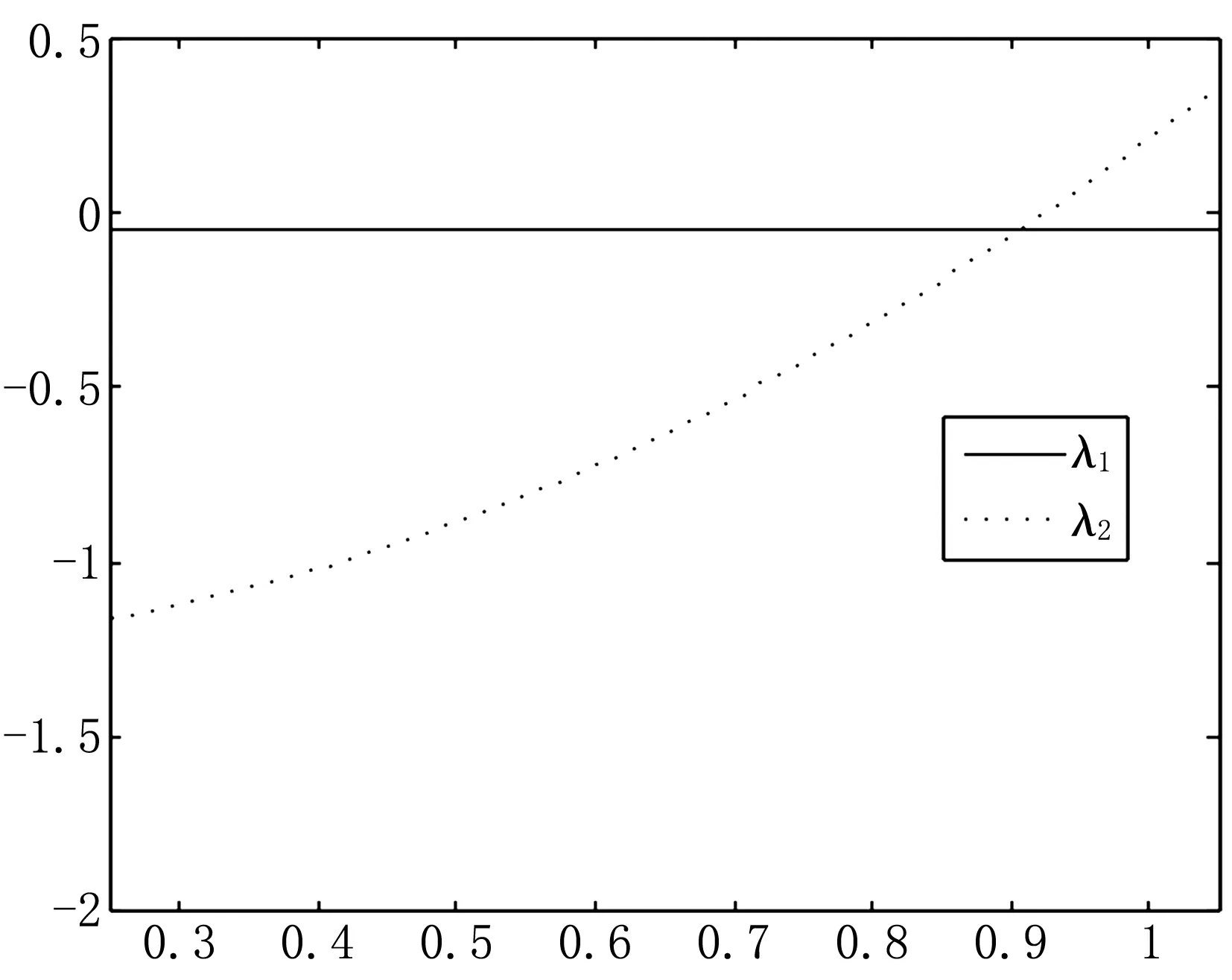
图1 实频率曲线图

再计算在上述节点处的两阶实频率的一阶灵敏度值，同样利用三次样条插值绘制这些实频率的一阶灵敏度的拟合曲线图，如图2。其中在每个节点处有必要检查非对称性对实模态解耦性能的影响：

1)在每个节点处的系统的实模态均能满足

φiTφi=1(i=1，2)。

2)在每个节点处的系统的实模态均不能满足式(21)～(23)：

φiTφj=0(i≠j；i，j=1，2)；

(21)

(22)

(23)

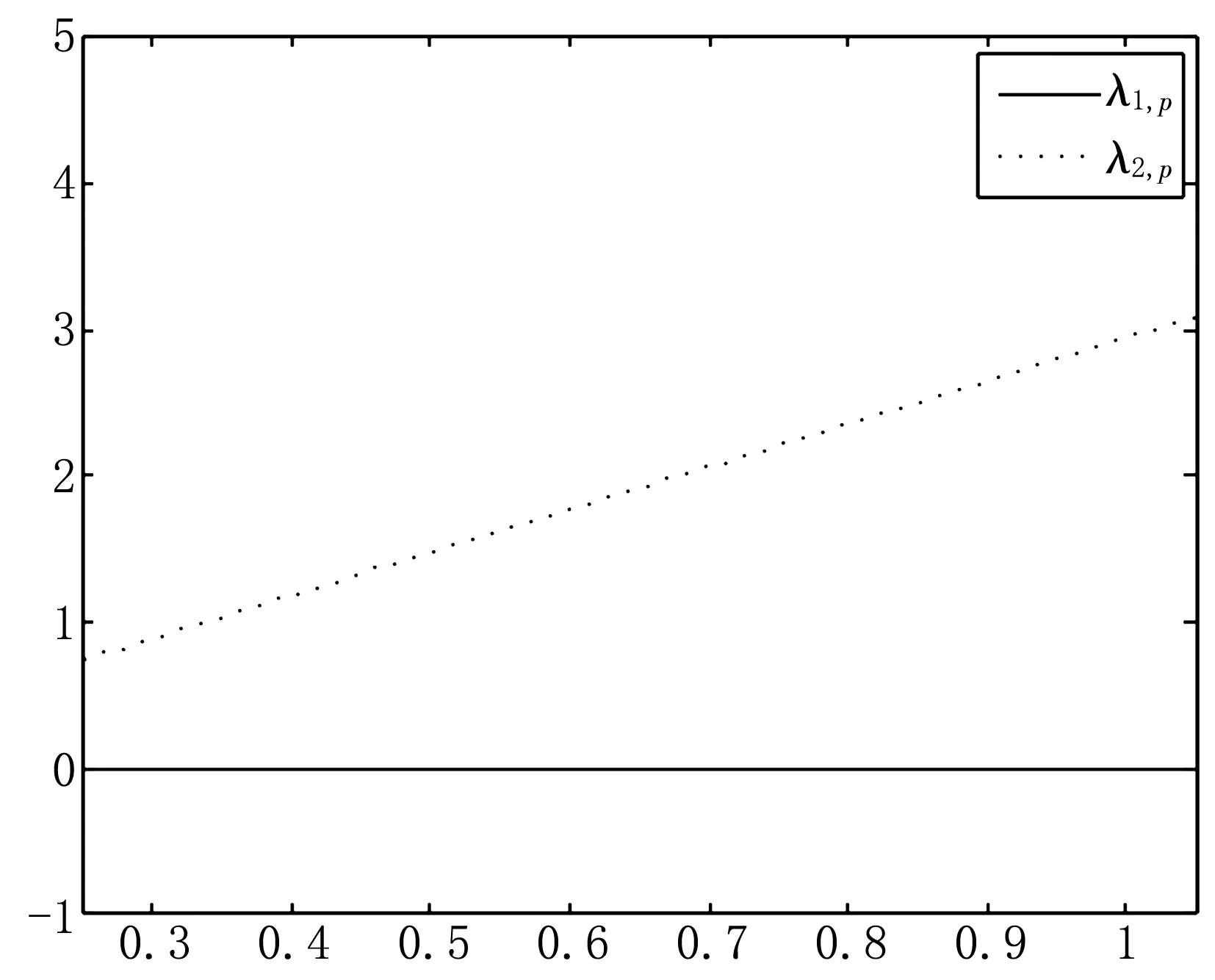
图2 实频率的一阶灵敏度曲线图

显然这些实模态本身并不具有良好的解耦性，这也是非对称系统的特性。因此，按本文的算法，在计算各阶灵敏度时，需引入左特征向量来实现解耦功能。

在图1～2中，我们发现实频率λ1，λ2的一阶灵敏度曲线图反映的是实频率曲线的几何性态。接着执行算法流程中第(8)～(9)步，计算在上述节点处的两阶实频率的二阶灵敏度值，同样利用三次样条插值绘制这些实频率的二阶灵敏度的拟合曲线图，如图3所示。

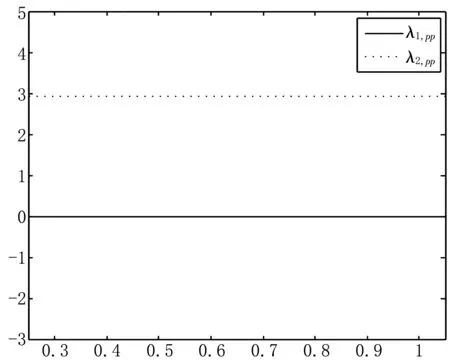
图3 实频率的二阶灵敏度曲线图

由图1～3可知，我们所绘制的这些拟合曲线图给我们提供了有效的信息。首先由图2可见节点处的实频率的一阶灵敏度能准确地反映实频率曲线在节点处的单调性。其次由图3可见节点处的实频率的二阶灵敏度能准确地反映了实频率在节点处的一阶灵敏度函数的单调性，同时反映了节点处的实频率曲线的凹凸性。最重要的一点是它们说明了本文算法计算结果的良好精度和应用性。

5 结语

在本文的研究中表明，无论是实频率的一阶还是二阶灵敏度，均伴随于与其相对应的实模态的一阶或二阶灵敏度的求解过程中。在求解实模态的一阶或二阶灵敏度的全模态展开式中的一阶或二阶灵敏度系数时，由于它们的灵敏度系数控制方程的降秩现象，虽然绝大多数灵敏度系数是可求的，却有一个灵敏度系数不能由灵敏度系数控制方程求得，但是由灵敏度系数控制方程相容性却可以确定实频率的一阶或二阶灵敏度。

本文的主要工作如下：

1)针对非对称系统提出了一种新的规范化方法，它包括对输出实模态的规范化，以及对与之正交的左特征向量的规范化，明确了规范化实模态的唯一性；

2)利用这种规范正交化关系解耦了一阶灵敏度系数的控制方程，从而同时求得了实模态的一阶灵敏度及实频率的一阶灵敏度；

3)利用这种规范正交化关系解耦了二阶灵敏度系数的控制方程，从而获得了实频率的二阶灵敏度算法公式；

4)提供了本文算法的流程和步骤，显示了本文算法的简洁性、紧凑性和实用性；

5)利用多节点计算灵敏度的数据处理方法，使数值算例的分析更加清楚直观。