公共物品供给“志愿者困境”博弈的实验经济学研究
周志波
一、引言
“志愿者困境”(volunteers’ dilemma),是一种公共物品供给的博弈困境,最优均衡只需一个志愿者为集体提供公共物品,但往往出现公共物品供给缺失或供给过剩的问题(Diekmann,1985[1];Diekmann,1986[2])。在志愿者困境博弈中,有若干个参与者,每个参与者都面临主动供给(牺牲自己的一部分利益)或者免费搭车两种选择(Goeree等,2017[3])。根据经济学的定义,典型的公共物品具有非竞争性和非排他性特征,这就意味着公共物品的使用既不会减少他人使用这一物品的机会,也不会阻止他人使用的权利(曲创和臧旭恒,2003[4];黄斯涅,2015[5])。鉴于公共物品的两大特征,在“理性经济人”假设下,以个人效用最大化为目标的个体会产生“搭便车”(free-riding)的行为(王霄和吴伟炯,2012[6])。从集体理性看,每个博弈者都应当选择牺牲自己的部分利益,但从个体理性看,每个博弈者都应当选择免费搭车,这就造成集体理性与个体理性的冲突,集体最优行为与个体最优行为出现背离。换言之,在志愿者困境博弈中,如果对公共物品的供给达到一定的水平,每个博弈者都获得所有公共物品的收益,但如果公共物品的供给低于这个设定的水平,每个博弈者的收益都为零,导致从个人角度而言最优的行为不同于从集体角度而言的最优行为。
按照博弈者(潜在志愿者)之间是否存在合作因素,可以将志愿者困境分为合作型志愿者困境(coordinated volunteer’s dilemma)和非合作型志愿者困境(uncoordinated volunteer’s dilemma)。Diekmann(1985)[1]提出了一系列与真实世界密切相关的非合作型博弈,成为公共物品供给志愿者困境研究的基准框架。n个人被判处有期徒刑10年,除非至少有1个人招供,任何招供的人将被判处有期徒刑1年,其余人将被释放。招供就属于志愿服务,在本质上是一种公共物品。只要有1个人愿意作为志愿者招供,整个集体都会受益;如果没有志愿者招供,所有人都不会从招供的公共产品中受益。集体中的任何个体,只有在确信其他人都不会做志愿者的情况下,才会有激励主动招供,为集体减刑提供公共物品;但如果招供的代价很大,个体将严格偏好于免费搭车行为,希望其他个体作为志愿者提供公共物品。这种博弈是一种非合作型志愿者困境博弈,多数博弈者都倾向于“搭便车”。实际上,因为博弈者之间无法进行协调合作,也可能存在过多的博弈者倾向于提供公共物品,这会导致资源浪费的结果,造成第二重社会困境。如果博弈中不止1个人愿意做志愿者,但只有1个人会被随机选择作为志愿者,因而不会有多余的志愿服务,这就是合作型志愿者困境博弈。在这种合作协调的博弈模型中,1个志愿者最大化地承担了提供公共物品的成本,导致不同的策略集和潜在结果(宋紫峰等,2011[7])。
非合作型志愿者困境博弈在现实中有很多例子,涵盖组织性的、生物性的、技术性的志愿者困境问题。在n个人参与的非合作型志愿者困境(N-person uncoordinated volunteer’s dilemma)基准博弈中,每个人都面临一组二元性选项,其中包括一个代价昂贵的志愿决定和一个不做志愿者的选择。只有1个志愿者需要提供公共物品,其他的志愿者对公共物品的供给水平或者参与这个非合作型博弈的成本没有影响。Weesie(1993)[8]把这一博弈思想应用到日常生活行为的分析,比如,家庭决定由谁倒垃圾、夫妻决定谁半夜起床安慰哭泣的婴儿,等等。Murnighan等(1993)[9]举例说明一组士兵看到敌人手榴弹落入战壕的志愿者困境,跳起来掩护手榴弹的士兵可以救战友,但却要牺牲自己的生命。Archetti(2009)[10]甚至讨论了几种动物的志愿者困境,比如依靠警告防御捕食者逼近的脊椎动物,发现被捕食者的个体可能有足够的能力警示自己的族群,但作为志愿者可能吸引捕食者的注意,甚至成为捕食者的“盘中餐”。Johnson(2002)[11]分析了一个更贴近时代的例子,即开源软件开发的志愿服务。开源软件只需一个程序员开发作为公共物品的软件,但这会给自己带来成本,而其他所有人都可以从开源软件中受益。在这些非合作型博弈中,冗余的志愿行为可能存在,但也很浪费资源,有且仅有1人提供公共物品,将导致唯一的“最佳”或社会最优均衡。
关于合作型志愿者困境博弈,在现实生活中也很常见。其中,最著名的就是小鸡博弈(也称“鹰鸽博弈”)。正如Ochs(1995)[12]的研究表明,多轮博弈中博弈者可能表现出自适应学习策略,并最终实现混合性均衡。小鸡博弈在激励方面相当于志愿者困境。在这个著名的博弈中,两个博弈者必须在停下(staying)和转弯(swerving)之间做出一种选择,但两个博弈者都严格偏好于“一个停下一个转弯”的结果,因而没有占优均衡策略。De Heus等人(2010)[13]的实验研究表明,在小鸡博弈中,博弈者比在囚徒困境博弈中更合作。他们认为,博弈者觉得在小鸡博弈中背叛是更具有风险性的选择,但其风险性不如囚徒困境博弈中的背叛行为。Diekmann(1993)[14]专门研究了不对称志愿者困境博弈中的合作问题。Bergstrom等(2015)[15]在一个合作型志愿者困境博弈中分析了个人偏好问题,测试“让我来做”(let-me-do)的偏好类型对不同成本和公众认可的反应。关宏宇等(2015)[16]研究了规则公平偏好对个体公共物品志愿供给的影响。宋紫峰等(2011)[7]也做了类似的研究,并进行了实验经济学检验。
有关志愿者困境博弈的理论分析文献已经十分丰富,并做出了理论预测(如Diekmann,1985[1];Franzen等,1995[17]),社会心理学研究也通过现场实验(Darley和Latané,1968[18];Darley和Latané,1970[19])进行了检验。Murnighan等(1993)[9]的研究发现,在MBA学生的课堂实验中,随着群体规模的扩大,参与者作为志愿者供给公共物品的概率将下降。Goeree等(2017)[3]探讨了群体规模与志愿行为的关系。纳什均衡预测:博弈者成为志愿者的概率是群体规模的递减函数,并且选择不做志愿者这一结果的概率会随着群体成员的增加而上升。对群体规模n=2,3,6,9,12分别进行实验检验,结果发现理论预测的前一部分成立,但后一部分却不成立。Archetti(2009)[10]发现博弈者之间的联系越紧密,个体成为志愿者的可能性越高,特别是对于数量较大的集体,这种趋势表现得更为明显。虽然成为志愿者的概率仍然随着群体规模的增加而降低,但当博弈者之间的关联度很高时,出现不做志愿者结果的概率会随着群体规模n的增加而降低。此外,Weesie和Franzen(1998)[20]通过邮寄问卷调查,分析了成本分摊对志愿行为的影响。
虽然实验经济学方面的文献对志愿者困境相关的研究已经做了较多贡献,但来自实验经济学的证据仍显不足,很多独特的问题没有得到足够的关注(罗俊等,2015[21];Luo等,2017[22];Chen等,2013[23])。特别是,大量真实世界的类似情况暗示存在潜在的外部有效性,而现有的文献鲜有考虑与现实世界一致的志愿者困境的各种不同重要特征。这些不足,归纳起来主要是几个方面:一是对博弈者的异质性考虑不够。多数文献假设所有博弈者都是同质的,具有类似的特征,但事实是多数情况下现实中的博弈者都是异质的,这种异质性体现在性别、收入、教育层次、宗教信仰以及提供公共产品的成本等方面(连洪泉和周业安,2015[24])。Diekmann(1993)[14]研究了不同层次的志愿者成本矩阵问题,宋紫峰和周业安(2011)[25]用实验方法分析了收入不平等对公共物品自愿供给行为的影响,张元鹏(2016)[26]、Babcock等(2017)[27]还研究了性别对志愿者困境博弈行为的影响,但相关的研究在解释为什么会出现这样的结果方面仍需深入。二是对博弈中的不确定性问题研究不够。虽然已有文献关注博弈中的不对称信息问题,但这种不对称信息主要是不知其他博弈者采取何种策略的笼统假设。并且,绝大多数研究都认为,不确定性会降低博弈者提供公共物品的激励(或概率),但在实践中确实存在不确定性增强志愿服务激励的反直观现象,而很少有文献对此进行深入分析。三是对博弈中合作的潜在可能性研究不足(连洪泉,2016[28];邓红平和罗俊,2016[29];汪毅霖和王国成,2016[30];周业安等,2014[31])。实际上,现实的博弈有时存在外部有效性,具有诱导合作的潜在可能性。Hillenbrand和Winter(2017)[32]在这方面做了比较有代表性的研究,他们同时考虑不确定性和合作的潜在可能性,检验了一次性博弈,发现与已知博弈者数量的情形相比,潜在可能的志愿者数量的不确定性提高了合作的可能性。但相关研究还需拓展维度,因为外部有效性的范畴很广。四是对博弈者提供志愿服务的有效性和可靠性的背离问题分析不足。志愿者困境博弈的纳什均衡,往往出现理论预测与实验结果不一致的情况,这实际上就是志愿者的有效性和可靠性相背离的现象。对称性志愿者困境博弈的研究(Diekmann,1985[1])通常集中在对称混合策略均衡;而不对称志愿者困境博弈的研究往往关注不完全信息博弈的贝叶斯-纳什均衡(Weesie,1994[33];Johnson,2002[11])。这种混合均衡具有反直觉和反证据性质,一般违背直觉结果,也与实验结果矛盾。在一个不对称的志愿者困境博弈中,可能出现供给成本越低提供志愿服务的概率也越低的荒谬结果。Myatt和Wallace(2008)[34]针对这一现象指出:志愿者不必是成本最低的博弈者,成本相对较高但可靠性更高的博弈者会提供志愿服务,当高价值与低成本并存时,更加有效的博弈者会提供志愿服务,这为现代开源软件的开发问题提供了一种解释。
本文将在Diekmann(1993)[14]、Goeree等(2017)[3]的非合作型志愿者困境博弈中,引入博弈者异质性和不确定性因素,研究博弈者提供公共物品(志愿服务)的有效性和可靠性背离问题,并分析这种异质性和不确定性如何影响博弈者提供志愿服务的可能性以及集体提供公共物品的效率。博弈者的异质性主要考虑不同的博弈者具有不同的“志愿服务能力”,这种不同的能力用博弈者提供公共物品的不同成本作为替代变量;不确定性主要考虑不对称信息因素。我们的研究与Diekmann(1993)[14]、Goeree等(2017)[3]的模型主要有四个方面的差别:(1)考虑了博弈者异质性问题,引入了博弈者提供公共物品的成本差异,并进而分析这种不对称均衡。(2)考虑了博弈中不对称信息的问题,并比较分析了完全信息和不完全信息条件下理论预测与实验结果的差异。(3)为了研究决策者数量对博弈者决策行为及均衡结果的影响,Diekmann(1993)[14]比较了n=2,5两种博弈规模,Goeree等(2017)[3]分析了n=2,3,6,9,12五种博弈规模的情况,但为了简化问题并不失一般性,我们只考虑n=2,6两种特殊情况。(4)为了简化分析,对博弈矩阵参数做了特殊赋值处理。假设博弈中至少有1个人提供志愿服务,n个博弈者的收益为1;没有任何人提供志愿服务时,n个博弈者的收益均为0。
实验结果表明:(1)博弈者提供公共物品的激励总体上随成本的增加而降低。完全信息条件下,当博弈者面临不对称成本时,低成本(或者强激励)的博弈者(提供志愿服务的概率为81.48%),明显比高成本(或低激励)的博弈者(提供志愿服务的概率为11.11%)更愿意作为志愿者,提供公共物品。(2)博弈者提供公共物品的有效性与可靠性并不总是一致。低成本的博弈者并不总是提供志愿服务,这一结果支持了低成本、高能力的博弈者可能不可靠的理论。(3)不确定性对个人志愿服务的可能性有积极影响。当模型引入不完全信息因素时,保持其他条件不变,博弈者提供志愿服务的平均比率由36.34%上升至47.34%(双侧t-检验p=0.005)。(4)不确定性由于损害集体提供公共物品的效率,其对志愿服务激励的积极影响并不会促进集体福利帕累托改进。不确定性在增强志愿行为激励的同时,可能不止1个博弈者有提供公共物品的行为,而多余的“牺牲”却损害了集体的效率,在不确定性条件下社会效率并未提高。
本文的研究贡献主要有两个方面:第一,在研究框架层面,将现有文献关注不够的异质性(不对称成本)和不确定性(不对称信息)因素同时纳入分析框架,并通过实验检验二者对策略性决策的影响。第二,在研究结果层面,从经济实验中获得了三种反直观现象的实证证据。三种反常现象即:(1)博弈者提供公共产品的有效性与可靠性不一致,为Diekmann(1993)[14]和 Weesie(1993)[8]类似的理论预测提供了实验证据;(2)不确定性对博弈者提供公共物品的潜在可能性具有积极影响,这验证了Weesie(1994)[33]的理论预测;(3)对志愿服务的积极影响并不会带来集体福利的帕累托改进,这是非合作型志愿者困境的特殊性使然。
本文的结构安排如下:第二部分介绍实验设计和博弈模型;第三部分为实验结果及经济解释,除了此前介绍的一些结果外,我们还分析了路径依赖如何在志愿行为决策过程中发挥作用,以及博弈者的偏好类型如何影响志愿行为;第四部分为结论。
二、博弈模型和实验设计
(一)理论模型
1.基本博弈模型。
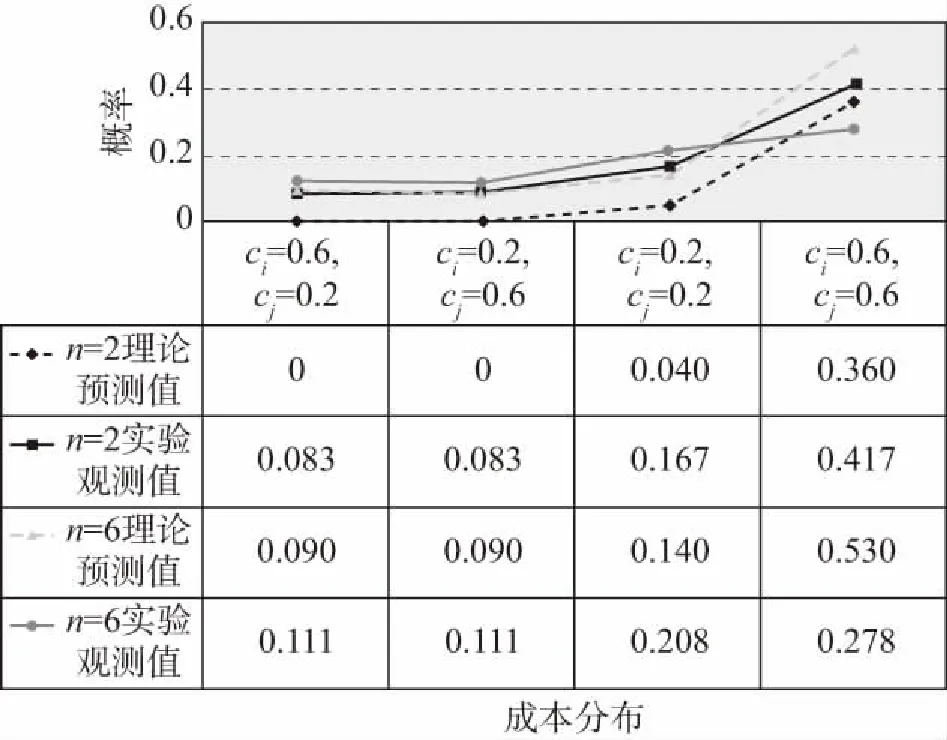
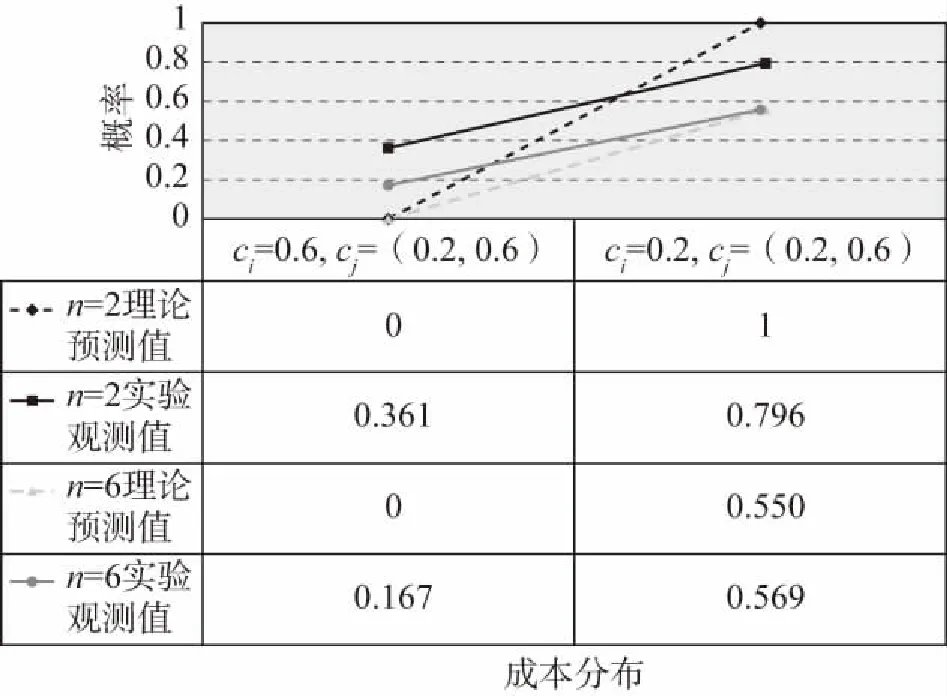
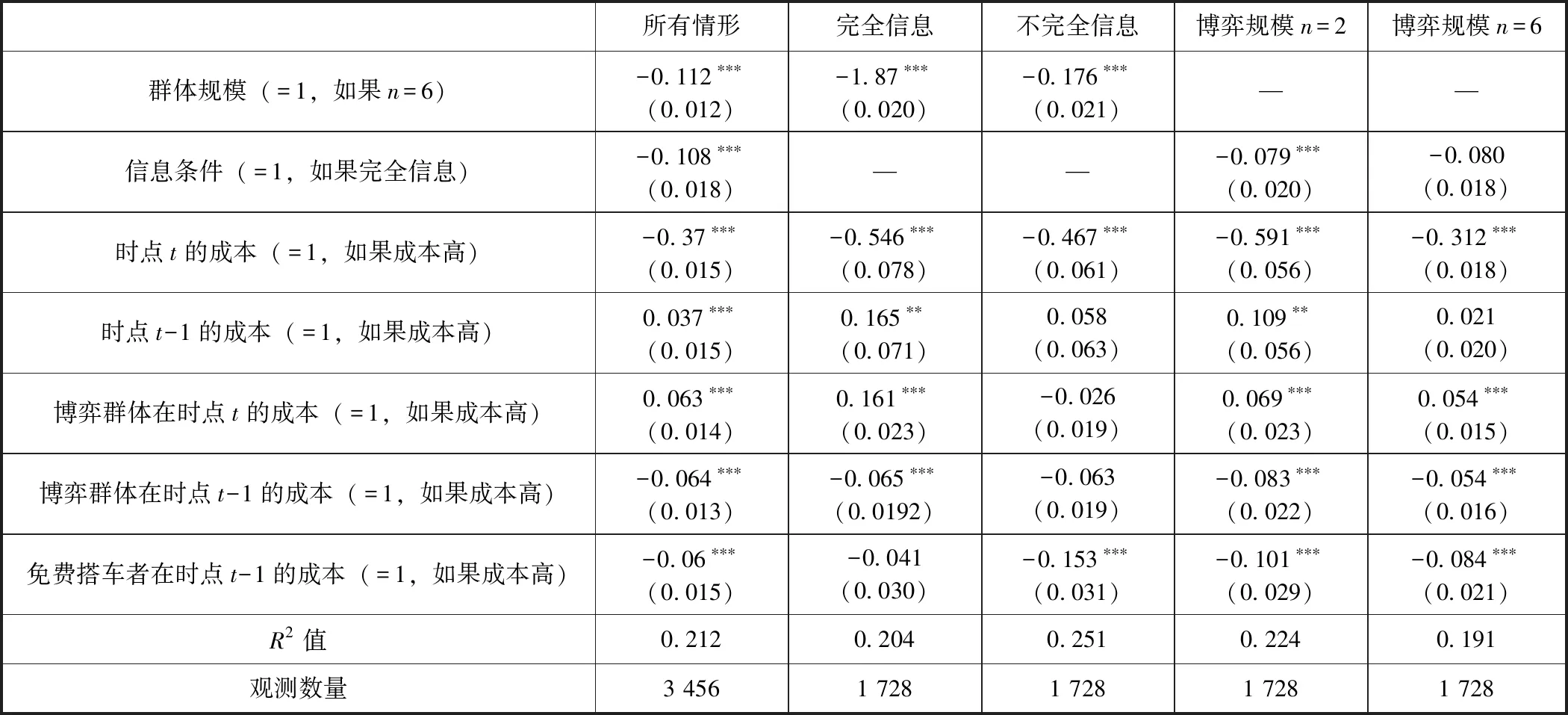
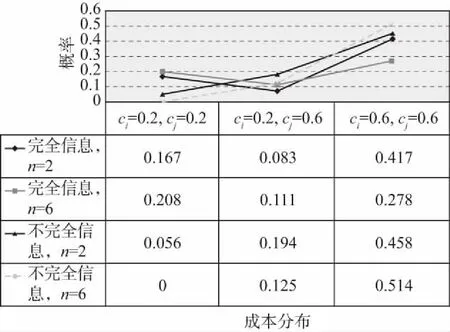
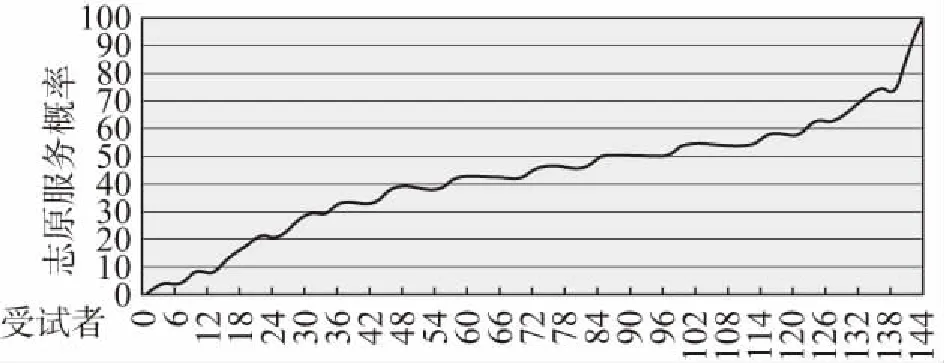
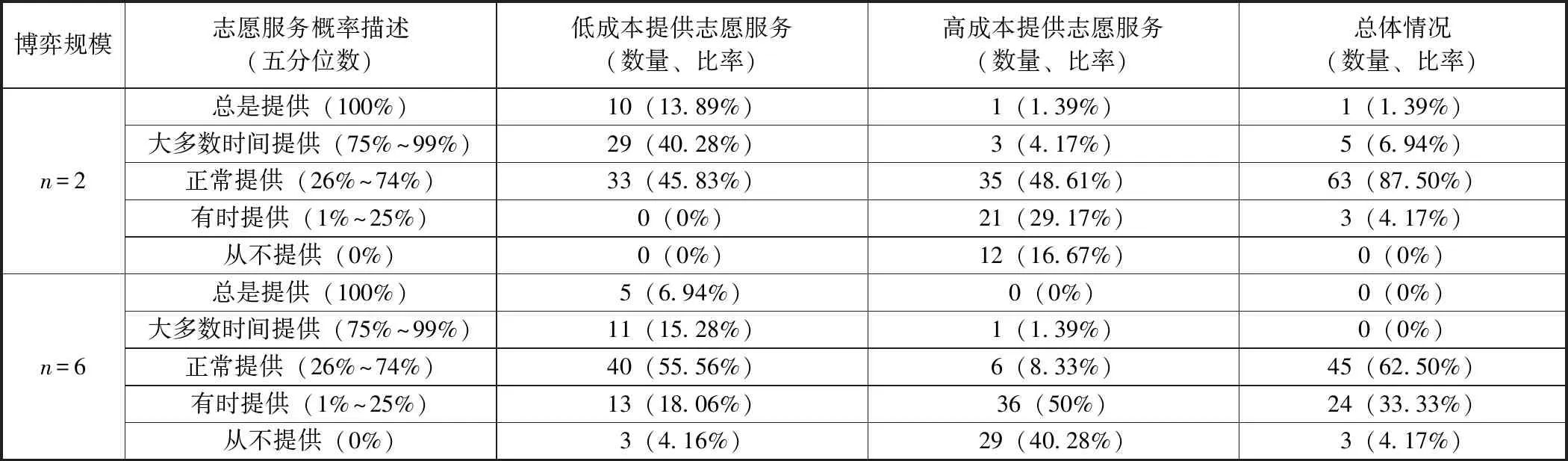
博弈设置如下:n个受试者参与博弈,如果至少有1个博弈者i=(1,2,...,n)以ci的成本提供公共物品(志愿服务),n个博弈者均获得货币性收益B;如果没有人做志愿者,n个博弈者都获得一个较低水平的收益K。由于B>K,每个博弈者都偏好有人提供公共物品的均衡,但都希望其他的人做志愿者。不过,假设ci 我们引入博弈者成本异质性,即每个博弈者都可以选择是否提供志愿服务,但不同的博弈者提供志愿服务的成本不同。志愿者i的成本ci>0,ci∈(cL,cH),cL和cH分别表示低成本和高成本。为了简化分析,假设K=0。换言之,如果至少有1个人提供志愿服务,所有博弈者获得收益B。如果没有人提供志愿服务,参与博弈的n个博弈者收益都为0。因此,只要ci W是=B-ci (1) 2.不对称均衡。 假设博弈者i不提供志愿服务的概率为qi,提供志愿服务的概率为pi,则有pi=1-qi。博弈者i的目标为实现期望收益Ei最大化,即 (2) 一阶条件为: (3) 可以得到不对称均衡解 (4) (5) 所有博弈者都不提供志愿服务的概率为 (6) 至少有1个博弈者提供志愿服务的概率为 (7) 为了进一步简化分析,我们假设B=1,可以得到更为简化的不对称均衡解。 3.对称均衡。 特别地,如果博弈者成本对称,即满足ci=c,B=1,并且限制0 (8) 从而,博弈者i提供志愿服务的概率为 (9) 所有博弈者都不提供志愿服务的概率为 (10) 至少有1个博弈者提供志愿服务的概率为 (11) 以上的不对称均衡和对称均衡都是理论预测均衡,也是直觉的均衡。我们将利用这些公式和实验参数来分析众多对称、不对称和混合策略纳什均衡预测,区分直觉的均衡和与社会效率相关的反直觉的均衡。然后,考虑志愿服务成本的变化如何影响博弈小群体(n=2)和大群体(n=6)的行为。最后,研究如何将不完全信息建模为具有一般先验知识的贝叶斯博弈,并分析成本不确定性如何改变决策行为。 本实验在西南大学进行,受试者为网络招募的144名本科学生志愿者。对B(如果至少有1个人提供志愿服务,受试者获得的收益)和K(如果没有人提供志愿服务,受试者获得的收益),实验分别赋值为1元、0元。实验设计了10个实验阶段,在实验组规模为n=2,n=6时,分别测试完全信息和不完全信息条件下,成本异质性(不对称成本)如何影响博弈结果。同一受试者提供志愿服务的成本会在同一阶段的博弈中发生变化,但信息条件和实验组规模会在不同的博弈阶段发生变化。虽然志愿者的决定是二元性的,实验设计提供了一个潜在纳什均衡预测。表1给出了相关的设计和处理。 在所有的实验阶段,博弈者提供志愿服务的成本要么为0.2元,要么为0.6元。当n=2时,提供志愿服务的成本组合(自己的成本/其他博弈者的成本)可能是:0.2元/ 0.2元、0.2元/ 0.6元、0.6元/ 0.2元,或0.6元/ 0.6元。n=6时,提供志愿服务的成本组合可能是:0.2元/其他5人均为0.2元,0.2元/2名0.2元、3名0.6元,0.6元/2名0.6元、3名0.2元,0.60元/其他5人均为0.6元。每个博弈者(受试者)的成本在每一轮博弈中随机抽取,因此他们面临的志愿服务成本为0.2元或0.6元,其概率分别为50%;其他博弈者的成本为0.2元或0.6元的可能性也分别为50%。换言之,如果n=6,成本抽取为0.6元的受试者知道,要么6人的成本都为0.6元,要么3人成本为0.2元、3人成本为0.6元,二者的概率各为50%。在本实验中,这些成本实际上都是在每一轮博弈中随机抽取的,以确保实验过程中所经历的成本变化和次序的一致性。 表1 实验设计 在完全信息条件下,博弈者知道自己的成本,并能推测其他博弈者的成本(尽管在6个人的博弈中,并不确切知道每一个人的成本分布)。在不完全信息条件下,受试者(博弈者)知道自己的成本,并且知道其他博弈者的成本可能更高,也可能更低,概率各为50%,但并不能推测其成本的具体值。举例说明,在6人博弈中,一个受试者面临0.2元的成本,可能知道至少有2个博弈者的成本相同(0.2元),另外3个人的成本可能为0.2元,也可能为0.6元,概率分别为50%。每轮实验结束时,受试者观察是否有公共物品供给,而不用观察参与博弈的人数。这样做的目的在于不鼓励或支持在实验中学习适应,使每个博弈回合相互独立,以测试志愿服务的可能性如何因成本和信息条件差异而不同。因此,我们在不同轮数的博弈之间提供尽量最小化的信息,这种信息严格地限制在是否至少有1个志愿者,这实际上可以通过被试者每轮的收益推论出来。 每一阶段的博弈持续24轮,每轮博弈的人员都随机地重新组合,所有受试者都保持匿名,以防在博弈中建立某种“声誉”,避免合作共谋的可能。当n=2和n=6时,在完全信息和不完全信息条件下,四种成本分布下各有864个实验观测值,整个实验有3 456个观测值。 每个博弈者抽到高成本或低成本的概率都是相同的,因而对数量为n的博弈集体而言有三种情况:所有人都具有对称的高成本,所有人都具有对称的低成本,或者存在成本不对称性(一半的人低成本,一半的人高成本)。如果至少有1个人提供志愿服务,所有人都获得收益1元。完全信息条件下,在做出决策之前,每个博弈者都被告知博弈集体成本随机抽取的情况。在Diekmann(1985)[1]成本对称的两组实验中,当n=2时,两个博弈者都面临相同的成本,两人都采取混合策略——面临成本c,提供志愿服务的概率p满足等式p=1-c。博弈者要么提供志愿服务,保证自己获得确定的收益1-c,要么不提供志愿服务,获得期望收益p。表2列出了博弈者在不同信息、成本和博弈规模下相关决策概率的理论预测值。 表2 博弈者在不同博弈规模和信息条件下决策的纳什均衡理论预测值 注:表格中的数据由于乘方开方的原因,可能会出现很小的情况。为了便于分析,所有数据最多保留3位小数,超过3位小数的部分被“去尾”。 在完全信息的情形下,更为直观的纳什策略导致低成本博弈者志愿服务的概率更高,这会促进社会效率的极大提升。因而,我们提出涉及特殊均衡的两个实验假设(下标H(L)表示高(低)成本): 假设1:博弈者提供志愿服务的概率p将表现出如下的成本特征:对pi|j(其中i是第i个博弈者的成本类型,j在当n=2时代表另外1个博弈者的成本类型,在n=6时代表其他3个博弈者是否面临与其相同的成本类型),可以推论: pH|L (12) 假设2:出现无人提供志愿服务结果的概率P随着博弈规模的扩大而上升,当n=6时这一概率值(P=0.212 5)超过当n=2时该概率值(P=0.10)的2倍。 模型建立为一个具有共同先验信息的贝叶斯博弈(Bayesian game),每个博弈者都知道自己在每一轮博弈中的成本以及其他博弈者的成本分布,但并不知道给定某轮博弈的结果。当n=2时,博弈者i可以提供志愿服务并获得确定收益1-ci。当自己的成本较低时采取这样的志愿行为策略,因为另一个博弈者的成本是在cL和cH之间独立地随机抽取的,不提供志愿服务的期望收益为0.5。对c=0.2的博弈者而言,提供志愿服务有保证的收益率是0.8。因此,给定期望收益,成本较低的博弈者往往倾向于提供志愿服务。如果成本c=0.6,提供志愿服务的收益为0.4,而不提供志愿服务的收益仍然为0.5,成本较高的博弈者应该永远都不提供志愿服务。因此,存在一个对称的纯策略贝叶斯-纳什均衡(Bayes-Nash equilibrium),两个博弈者在成本都较低时都会提供志愿服务,但在成本都很高时都不会提供志愿服务。表2的下面一部分给出了对称成本条件下提供志愿服务的概率以及出现无人提供志愿服务结果的概率。当n=6时,采用低成本者提供志愿服务而其他博弈者不提供志愿服务的纯策略,不存在贝叶斯-纳什均衡。但是,又存在一个直观的混合策略均衡,低成本博弈者以p<1的概率提供志愿服务,高成本博弈者不提供志愿服务。如果低成本博弈者以p的概率提供志愿服务,那么每个博弈者都会预期其他博弈者都以概率p/2提供志愿服务。在这种情况下,其他5个博弈者都不提供志愿服务的概率为1-(1-p/2)5。这里,低成本者提供志愿服务的收益是0.8,如果1-(1-p/2)5=0.8,低成本者就会以p的概率提供志愿服务。当n=6时,p=0.55。表2的下半部分给出了这一均衡预测以及6人组博弈集体中无人提供志愿服务结果的概率预测。在不完全信息条件下,直观的纳什策略预测的志愿服务概率如下: 假设3:博弈者提供志愿服务的概率p表现出如下的成本特征:对pi(其中i是第i个博弈者随机抽取的成本类型,博弈者i并不知道其他博弈者是否面临相同或不同的成本类型),可以推论: pH (8) 假设4:均衡状态无博弈者提供志愿服务的概率P随博弈群体规模的增加而增长,这种趋势在n=6(P=0.297)时比n=2(P=0.25)时表现得更为明显。 尽管不确定性可能增强提供志愿服务的激励,但总体而言,保持其他条件不变,相对博弈者对成本具有完全信息的情况,在不完全信息条件下出现无人提供志愿服务结果的可能性仍然很高。在完全信息情形,识别什么时候存在不对称成本的能力,有助于博弈者发现“合意的”志愿服务者(可能是他们自己,也可能是其他人)。在不完全信息情形,博弈者可能在成本较低时提供过度志愿服务,而在成本较高时提供志愿服务不足,特别是在对称成本条件下,这一趋势表现得尤为明显。因此,虽然在不完全信息条件下可以看到志愿服务的增加和社会福利的提升,但即便是“更为直观的”均衡策略都不会将其预测为博弈的结果。在第三部分,我们将通过实验检验以上提出的四个假设,并展开深层次分析。 实验数据中出现了一些值得注意的结果。表3和表4给出了每一种情形下的志愿服务概率,并将结果分为四种成本分布类型:(1)同一组所有受试者成本较低;(2)同一组所有受试者成本较高;(3)1个受试者面临c=0.2的较低成本,而组内至少有另外1个受试者面临较高成本;(4)1个受试者面临c=0.6的较高成本,而组内至少有另外1个受试者面临较低成本。 表3和表4中括号内的数字表示博弈纳什均衡概率的理论预测值,这些数字来源于表2,并换算成为小数形式,所有数据最多保留两位小数。 表3 完全信息条件下志愿服务数量和概率(p)的实验观测值 表4 不完全信息条件下志愿服务数量和概率(p)的实验观测值 总体而言,受试者的行为与更直观的纳什均衡策略的理论预测保持一致,这种一致性在完全信息情境下表现得更为突出。比较分析结果表明,尽管不完全信息提高了志愿服务概率,但完全信息的情形仍然是更具有社会效率的结果。 接下来,分别对完全信息和不完全信息的情境进行分析讨论。 首先,从完全信息和对称成本出发,比较表3的第4行低成本(c=0.2)与第5行高成本(c=0.6)时的p值。发现受试者在成本较低时比成本较高时更愿意提供志愿服务。当面临较低的成本时,受试者表现得更愿意做出牺牲、分担责任,n=2时提供志愿服务的概率为65.28%,n=6时提供志愿服务的概率为39.81%。相反,当所有受试者都面临较高的成本时,提供志愿服务的概率明显下降,当n=2时为24.54%,n=6时为15.74%。 图1展示了第三部分完全信息情境下理论预测与实验结果的差别。特别是,n=2、成本对称且较高(ci=0.6,cj=0.6)及n=6、成本对称且较低(ci=0.2,cj=0.2)时,实验数据与直观的纳什均衡预测结果高度一致。但是,当n=2、成本对称且较低时,志愿服务提供不足(概率观测值p=0.491,理论预测值为0.8);而n=6、成本对称且较高时,博弈者倾向于过度志愿服务(概率观测值p=0.269,理论预测值为0.1),这验证了Goeree等(2017)[3]关于博弈群体规模影响志愿服务概率的结论。 图1 完全信息条件下博弈者i提供志愿服务概率的实验观测值和理论预测值 现在,将上述分析拓展至完全信息但成本不对称的情形,发现受试者在成本较低(提供公共产品的能力更强)时,更愿意提供志愿服务。当n=2,ci=0.2,cj=0.6时,受试者i提供志愿服务的概率最高为p=0.815。当n=6,ci=0.6,cj=0.2时,受试者i提供志愿服务的概率最低为p=0.046。对pi|j,i为博弈者i的志愿成本类型,j代表其他博弈者的成本类型,表3和表4中的实验观测数据表明,n=2和n=6时假说1都成立: pH|L(0.111 1) (9) pH|L(0.046 3) (10) 完全信息、不对称成本情境的实验证据表明,一个博弈者相对于其他博弈者的成本,在决策中具有重要的影响。我们发现提供志愿服务的概率与其他博弈者的成本正相关,这说明人们在他人成本相对较高时更愿意提供公共物品。这也表明,个体决策都是围绕有效结果而做出的,换言之,博弈者在最有必要(自己的成本相对较低或者所有人的成本都很高)时做志愿者,以更好地保证有人提供公共物品,避免出现所有人都不提供公共物品而导致集体利益受损的情形。 为检验以上结论,控制一系列主体特征变量,进行OLS回归分析,结果如表5所示。每一列表示一个独立OLS回归,其中第1行的变量为因变量,同一列中的其他变量为自变量。第1列检验了博弈规模、信息条件和博弈者的其他特征对博弈者提供志愿服务概率的总体影响。第2列至第7列分别检验了每一种情形(不同的博弈规模、信息条件、成本类型的组合)下的博弈结果。第1列的回归结果表明,总体而言,博弈规模从n=2增加至n=6,降低了博弈者提供志愿服务的可能性,再次验证了表3和表4中总体实验观测结果。进一步分析发现,除所有博弈者都面临较低成本的情形外,在其他3种成本类型分布下,博弈规模都对博弈结果有影响。 表5的最后一列将博弈者的收益对自变量进行回归,由于在实验中社会效率与博弈者的收益之间存在单调递增的关系,这一变量的系数可以作为整体效率的替代变量。正如表5所示,博弈规模的系数为正且显著,表明规模较大的群体在提供公共物品方面更有效率,因而我们没有发现支持假设2的证据。这可能至少在某种程度上,是由于存在某些“偏好类型”的博弈者(关宏宇等,2015[16]),我们在后面讨论。 接下来,分析完全信息条件下无人提供志愿服务的概率情况。正如Goeree等(2017)[3]指出的那样,理论对志愿者困境做了一个与博弈规模相关的直观结果预测:无人提供志愿服务的概率随着博弈规模的扩大而提高,在客观上起到一种分散责任的作用。图2比较了不同博弈规模下的实验数据和理论预测结果。当n=2,对所有成本分布类型,无人提供志愿服务结果的实验观测概率比纳什均衡预测水平更高,因此规模较小的博弈群体其实际行为与理论预测不太一致。 表5 提供志愿服务概率(p)的OLS回归结果 图2 完全信息条件下无人提供志愿服务概率的实验观测值和理论预测值 在实验中引入不确定性,给志愿者困境问题增加了另外一个分析维度。尽管仍有四种可能的结果,但这些结果在每一个博弈者看来实际上就是两种结果:要么面临较低的成本(0.2元),要么面临较高的成本(0.6元)。不论何种情形,博弈中一半的人成本类型相同,一半的人成本类型不同,并且这两种情况出现的几率相等。 前面的分析发现,在完全信息条件下,成本较低时的志愿服务概率明显高于成本较高时的志愿服务概率。表4展示了不完全信息博弈实验阶段,面对不同的成本类型和不同的博弈规模,志愿服务的平均概率。图3给出了实验结果:当n=2时,成本较低时,受试者提供志愿服务的比率为79.63%,成本较高时这一比率为36.11%;当n=6时,受试者提供志愿服务的比率为56.94%,成本较高时这一比率仅为16.67%。因此,我们的实验观测数据与理论预测基本一致,支持假设3成立。 图3 不完全信息条件下博弈者i提供志愿 服务概率的实验观测值和理论预测值 图4给出了不完全信息情形中,不同博弈规模下,无人提供志愿服务结果的概率情况。总体而言,出现无人提供志愿服务均衡的平均概率随群体规模增加而降低(当n=2时P=0.225 5,当n=6时P=0.191),这与假设4相矛盾。 图4 不完全信息条件下无人提供志愿服务概率的实验观测值和理论预测值 为了比较不同信息条件下的实验结果,首先保持博弈规模不变,然后分析完全信息和不完全信息情形下提供志愿服务的比率。表6给出了一系列Probit回归分析结果,如果博弈者在当前博弈阶段提供了志愿服务,因变量就取值为1。从n=2开始,控制成本变量,博弈者在完全信息条件下提供志愿服务的概率明显更低。平均而言,当成本较低时,博弈者在不完全信息条件下提供志愿服务的比例为79.63%,但在完全信息条件下这一比率为65.28%。当成本较高时,博弈者在不完全信息条件下提供志愿服务的比例为36.11%,但在完全信息条件下这一比率为24.54%。然后在n=6时,控制成本变量,博弈者在完全信息条件下提供志愿服务的概率明显更低。平均而言,当成本较低时,博弈者在不完全信息条件下提供志愿服务的比例为56.94%,但在完全信息条件下这一比率为39.81%。当成本较高时,博弈者在不完全信息条件下提供志愿服务的比例为16.67%,但在完全信息条件下这一比率为15.74%。 表6 Probit回归结果 注:因变量是一个虚拟变量,如果博弈者在时点t提供志愿服务则取值为1;回归报告了概率系数,标准误在阶段级上聚集。 在其他条件不变的前提下,在不同信息条件下的结果,其最大的差异就在于当成本较低时:博弈者在不完全信息条件下提供志愿服务的比例为79.63%,但在完全信息条件下这一比率大约为65.28%。正如表6所示,信息变量的系数为负并且显著,表明在完全信息条件下博弈者提供志愿服务的比率降低。有趣的是,n=6与n=2两种情形下,完全信息效应的大小基本相当。不完全信息不仅提高了志愿服务的概率,而且在n=6与n=2两种情形下对志愿服务供给的效应看起来是相同的。 Probit回归结果验证了主要的结论:博弈群体规模扩大和完全信息都对博弈者参与公共物品供给具有负面效应,分别降低志愿服务比率11.2%和10.8%。总体上看,将志愿服务成本从0.2元提高至0.6元,导致志愿服务概率降低37%,但这种效应在不完全信息、n=2时最强,在完全信息、n=6时最弱。不管自身在本轮博弈中的成本如何,如果博弈中的其他人面临较高的成本,博弈者提供志愿服务的概率可能要高6.3%。毫无疑问,只有在完全信息情形,当一个博弈者确定地知道其他成员成本的时候,这种效应才可能出现。博弈群体规模对这种效应的大小和显著性并无实质影响。 最后,比较分析有关无人提供志愿服务的概率结果,因为在不确定的情况下志愿服务的平均比率提高,通过更少的信息,更高的志愿服务率让博弈群体具有实际提高社会效率的潜能。然而,正如表5所示,将博弈者的收益对信息条件进行回归时,信息条件的系数为正并且显著,表明在完全信息条件下提供公共物品的效率仍然比不完全信息条件下更高。更确切地讲,对Px|y(x为博弈中个体的数量,y代表信息条件,F为完全信息,I为不完全信息),结合观察到的无人提供志愿服务的概率(括号内的数字),可以发现: P2|F(0.187 5) (11) P6|F(0.177 0) (12) 图5展示了这四种情形下的实验结果。总体而言,在不完全信息条件下,出现无人提供志愿服务结果的概率比完全信息条件下更高。 图5 无人提供志愿服务的概率观测值 为了更好地理解志愿服务背后的个人动机,我们分析了实验因素、当前和前期结果如何影响个体在时点t的行为。表6所示Probit回归分析,包含了上一轮博弈中博弈者自身的成本和其他博弈者的成本等变量。如果上一轮博弈中,一个博弈者面临较高的成本,即便在控制其他博弈者在本轮博弈中的成本之后,他们在本轮博弈中提供志愿服务的概率大约高3.7%。但是,更进一步观察,这一结果只有在完全信息情形且n=2时才成立,这一条件表明,一个博弈者需要知道另一个博弈者面临较高成本,并且知道博弈中除了自己外只有1个人可以提供志愿服务。这一发现可能会捕捉到一种情形,在这种情形下,当1个博弈者面临较高的成本,他会被限制提供公共产品(志愿服务),进而在下一轮博弈中产生一个较小的志愿服务激励,而不论志愿服务成本有多高。 此外,我们检验了上一轮博弈的结果对受试者本轮博弈是否产生影响。在检验中,我们引入了一个搭便车的虚拟变量,如果受试者在上一轮博弈中不是志愿者,但仍有其他人提供志愿服务,则虚拟变量取值为1。即便在控制成本和信息结构之后,成功搭便车的受试者在本轮博弈中提供志愿服务的概率要低于6%。引入个体固定效应以控制提供志愿服务的总体倾向,结果仍然不会有改变。这表明,如果看到即便自己搭便车但仍然有人提供志愿服务的结果,博弈者更倾向于推卸志愿服务的责任。接下来,进一步探讨这种行为偏好。 志愿者困境背后潜藏的原因是个体之间偏好类型的存在及其如何影响特定一轮博弈的结果(邓红平和罗俊,2016[29])。尽管在至少有1个人提供志愿服务的情形下,每个人都比无人提供志愿服务的情况下“过得更好”,但存在一系列个人偏好,不仅决定了在这轮博弈中的行为,而且决定了在任何一次存在免费搭车可能的博弈中的行为。这些偏好类型,涵盖从纯粹免费搭车者(永久免费搭车者)类型(即便冒着出现无人提供志愿服务结果的风险也要免费搭车的人),到“让我来做”(let-me-do)类型(也叫自我牺牲类型,即从公共产品的供给中受益,但也从志愿服务的过程中获得某种非货币形式效用的人)的所有个人偏好,“让我来做”偏好类型可能就是Andreoni(1989)[35]所说的“温情效应”(warm glow)。其他人都介于纯粹免费搭车和“让我来做”的两种风险偏好之间,处于偏好自己想提供志愿服务和实际上不愿提供志愿服务的中间平衡状态。 Bergstrom等(2015)[15]采用了一个非常巧妙的时间序列的变量,确认受试者有多大比例属于“让我来做”(let-me-do-it)的类型、“不要让我来做”(no-not-me)的类型,以及不到万不得已决不提供志愿服务的“不得已而为之”的类型(last-resort-consequentialists)。假定博弈是非合作型的,并且存在多个志愿者的可能,尽管我们无法观测后面一种偏好类型的受试者,但实验中关于不对称成本的机制设计,允许我们根据受试者在24轮博弈中提供志愿服务的比率对其进行排序。特别是,可以根据受试者服务能力很强(成本较低)或较弱(成本较高)时提供志愿服务的概率,进一步分析不同的偏好类型对决策行为的影响。因此,可以识别相对于比例分担的偏好变化,如“让我来做”的类型在面临更高的成本时成为“不要让我来做”的类型。 图6显示了不同偏好类型的概率累积分布,对从纯粹的免费搭车者(志愿服务概率为0)到永久志愿服务者(志愿服务概率为100%)的所有类型进行了排序。几乎所有的受试者都介于二者之间,如果将累计分布均分为三段,受试者集中度最高志愿服务比例介于33.3%~66.7%之间。在144个受试者中,只有1个是永久自我牺牲者,4个纯粹的免费搭车者,但都是男性。 表7为不同偏好类型的概率分布。首先考虑“让我来做”的类型,当成本较高时的负面激励足以抑制提供志愿服务可能获得的任何非货币性福利的正面激励。当n=2且成本较低(c=0.2)时,约14%的受试者一直提供志愿服务;但当c=0.6时,这一比率下降至1%左右。当n=6且成本较低(c=0.2)时,约8%的受试者一直提供志愿服务;但当成本较高(c=0.6)时,不仅这一比率下降至0,第二档偏好(志愿服务率75%~99%)比率也下降至1%左右。这可能表明,在任何一轮博弈中,以货币衡量的志愿者非货币性福利,可能都低于0.4元。 图6 偏好类型的累积概率分布 表7 偏好类型的频率和分布 同样,免费搭车的激励也随着成本和收益而变化。当n=2且成本较低(c=0.2)时,0%的受试者提供志愿服务的比率低于25%;但当c=0.6时,纯粹免费搭车者的比例上升至15.28%。当n=6且成本较低(c=0.2)时,大约4%的受试者是纯粹的免费搭车者;但当c=0.6时,这一比例上升至40%左右。当然,提高公共物品供给效率,要尽量减少不必要的志愿服务,但又不至于出现都不提供志愿服务的结果,因为有相当比例的博弈所有的受试者都面临较高的成本。这些关于偏好类型的信息提供了关于“旁观者效应”(bystander effect)的明显证据,这种效应在较大规模的群体中更普遍。保持所有其他条件不变,更大规模的群体,不仅仅意味着有更多博弈者,还意味着免费搭车偏好者的比例可能也更高。然而,即使有更多的搭便车者,更大的群体仍然能够以更高的比率(概率)提供公共物品,因为至少有1个人志愿服务的概率更高。 对公共物品供给领域的博弈理论研究,经济学家们很早就开始了探讨,并已形成比较丰富的理论成果。但是,这些理论的预测缺乏经验数据的支撑。直到最近二十年,一些经济学家、心理学家、社会学家开始利用实验室受控实验对理论进行实证检验,为相关理论提供了越来越多的实验证据。近年来,实验经济学方法大量应用于公共物品供给领域的博弈论研究,特别是对自愿缴费机制和志愿者困境的实证检验。在关于志愿者困境博弈模型的实验经济学研究中,多数学者关注非合作型博弈和合作型博弈、两人博弈和多人博弈、不对称成本和对称成本、不完全信息和完全信息等博弈的主要特征,对博弈模型中的一些细小特征关注不够,并且综合考虑多种特征和因素的实验证据较少。 本文在志愿者困境博弈模型中同时引入不确定性(不完全信息)和异质性(博弈者不对称成本)两大因素,利用实验经济学方法,实证检验信息条件、成本分布、博弈规模等变量对决策行为的影响,并对实验中出现的“反直观”现象作出经济学解释。 研究发现:(1)博弈者的有效性和可靠性并不总是一致的,有时甚至背离“直观”结果。(2)博弈者提供公共物品的成本上升,会明显降低其提供志愿服务的意愿和概率,并且博弈者提供公共物品的概率与参与博弈的其他人的成本呈现正相关关系。(3)博弈者对其他博弈者志愿服务成本的不确定性有助于提高自身提供公共物品的概率。推而广之,有关其他博弈者提供公共物品能力的不完全信息带来的不确定性会增强博弈者自身做出牺牲、提供志愿服务的激励。(4)不确定性在提高志愿服务可能性的同时,却可能导致过度的志愿服务供给,因而并不必然改进社会福利。虽然有微弱的证据表明,志愿服务概率的提升主要通过降低所有人都不提供志愿服务结果的概率,可能提高博弈群体的集体福利,但志愿服务的增加可能并不会导致社会效率的帕累托改进,至少在实验中没有观测到这样的结果。隐藏在背后的逻辑可能在于:通常情况下,更多的信息会导致更高的效率,但是如果不完全信息提高了志愿行为的概率,那么就存在不完全信息有效提高效率的可能性。然而,非合作型志愿者困境博弈的不合作性质往往会导致多余的志愿服务,尽管个人层面上的合作程度更高,但效率的提高可能不会出现。在一个无人提供志愿服务的结果比较普遍的环境中,不确定性(不对称信息)的积极作用更大,但这种积极作用在给定的一轮博弈中带来的社会收益,必须超过当不止1个人提供志愿服务时导致的社会资源浪费。(5)志愿者困境博弈存在“旁观者效应”,多数人的偏好类型“随大流”,并对最终的均衡结果有重要影响。同时,实验观测数据表明,“旁观者效应”在更大的集体中表现得更为明显。在其他条件严格受控不变时,博弈集体的规模越大,潜在的志愿者越多,但与此同时,潜在的免费搭车者的占比也更高。尽管如此,博弈集体规模越大,能够提供公共产品的概率(比率)越高,因为集体中至少有1人愿意提供志愿服务的概率随博弈者数量的增加而提升了。 本文的研究为志愿者困境博弈中博弈者如何对异质性(成本相对变化)和不确定性(成本信息不透明)做出反应,提供了实验证据,并做出了经济学解释。虽然多余的公共物品(志愿服务)并不必然促进资源配置或社会福利的帕累托改进,但在很多情境下,提高志愿服务的概率(比例)有助于改善社会福利。在这样的情境中,本文的研究结论有助于理解人们提供志愿服务的动机和决策,有助于在公共政策决策中,创设一种有利于社会自我改进和提升的激励机制。 当然,本文的研究还存在一些不足。比如,博弈设计未考虑惩罚机制,对出现所有人都不提供志愿服务结果时,并不要求对参与博弈的各个个体实施惩罚(如进行罚款,让其收益为负等手段)。考虑到惩罚机制的因素,志愿者困境博弈可能出现反直观的结果(闫佳和章平,2016[36];张元鹏和林大卫,2015[37];连洪泉等,2013[38])。再如,本文只就n=2,n=6两种情形进行实验验证,有关博弈集体规模对决策行为影响的证据不够有力。此外,参与实验的受试者也是理性经济人,实验回报的多少可能对其对待实验的认真程度具有不可忽略的影响。但本文的研究没有考虑这一因素,较低的实验回报可能对实验结果有潜在的影响。同时,博弈者也可能存在“利他主义”偏好(Andreoni,1989[35]),这也会影响实验研究的结论。这些问题和不足,也是后续研究的方向。


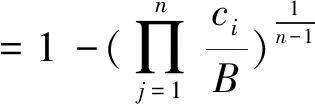
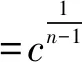
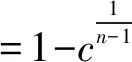
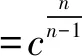
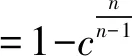
(二)实验设计
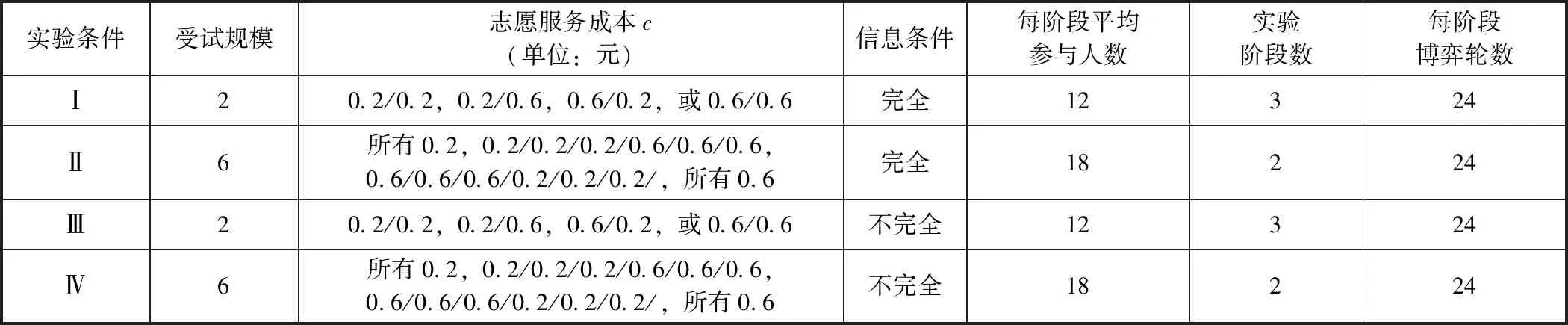
(三)完全信息情境
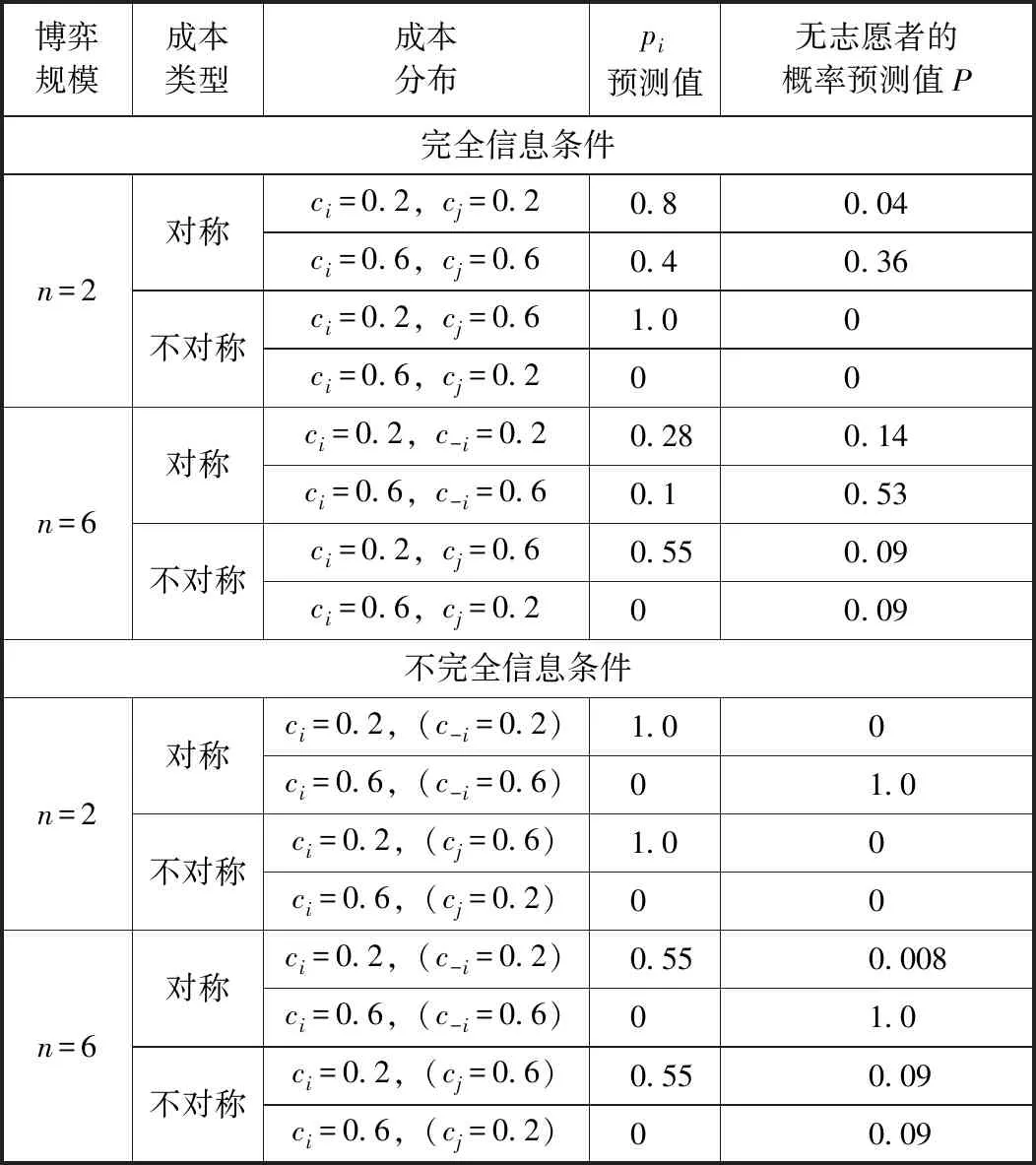

(四)不完全信息情境
三、实验结果分析解释
(一)实验结果
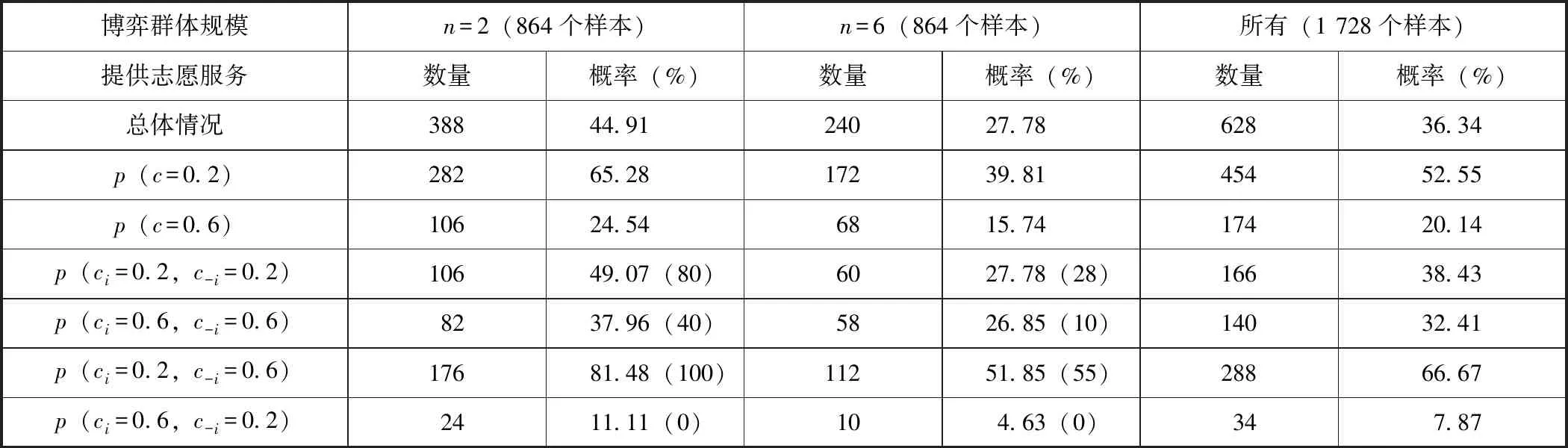

(二)完全信息情境的分析



(三)不完全信息情境的分析

(四)路径依赖效应
(五)偏好类型的作用
四、结论

