高等数学中极限概念的认识

盛辉

（安徽新华学院国际教育学院，安徽 合肥 230088）

一、极限的概念

（一）数列极限

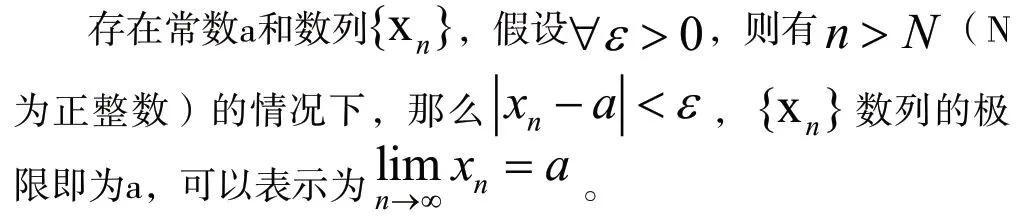
（二）函数极限

在数学发展的过程中，因为需求差异，对差异化极限理念进行了运用，集列上极限及下极限原理就在集论内有着一定的运用，级数条件收敛及绝对收敛原理也可以应用到无穷级数论方面[1]。除此之外，极限原理也能够应用到函数逼近论方面，例如：平均逼近定义和一致逼近定义等。纵观上述概念运用，能够发现基础原则均是由有限概念延伸至无限概念。

二、极限思想的价值

有限及无限、常量及变量间的联系均涵盖于极限思想中，借助极限概念，透过有限、直线近似和不变及量变能够对无限、曲线、变化和质变进行分析。所以，极限思想能够启发人们的创新意识，其在各个方面均发挥着不容忽视的作用，例如：微分几何、积分方程、力学、函数逼近论、微分方程和概率极限理论等。

借助实际例子来了解极限思想，比如如果有一块蛋糕，首先切掉一半，次日再切掉剩下一半的一半，第三天再切掉一半的一半的一半......以此类推，最终能彻底切完这块蛋糕吗？经过分析得知永远不可能完全切掉这块蛋糕，即使蛋糕每天在不断变小，但是依然还存在这块蛋糕。由此可以看出，蛋糕的极限就是0，并且≠0。极限思想就在这个例子中有着充分的体现。

众所周学习知极限思想非常关键，它也是学生难以理解掌握的重要概念，它贯穿整个数学体系，是一种非常重要的数学思想，它是人类发现并解决数学问题的非常重要手段，它能很好地展现出数学的思维之美，在高等数学的教学过程中起着相当重要的作用，恰当的应用极限思想不仅可以将一些问题简化，开辟解决问题的新途径，通过分析、总结、归纳得出极限概念中各变量具有的变化特征和内在练习，分析变化过程中的各种规律，还可以培养数学思维，提高解决问题的素质能力，因此，能够灵活运用极限思想有重要的意义。

三、极限定义的分类

多元函数极限、函数极限及数列极限等是构成极限的关键类型，基于各类极限，应对其定义进行充分的了解，从而掌握详细应用[2]。

（一）数列极限

对于数列极限的概念，假设存在数列{an}和确定数a，且具有正整数N，满足N＜n，对于任意正数ε，满足an -a<ε，那么数列{an} 收敛于a，数列极限就是a，表示为an→a（n→∞），也可以表示为lim n→∞ an=a。对于ε-N这一数列极限概念，涵盖的N、ε中，后者预先进行了设定，所以根本就是对N进行运算，同时ε会直接影响N值，也能够表示成N=N（ε）。

上述概念内的常数ε存在二重性的特点，代表正数固定程度不强，存在随意小任意性。在ε保持不变的情况下，能够明确逼近程度；如果ε在不断变化，如果在任意小的情况下，就能够刻画其逼近无限性。

通常N取值会随着ε的不断减小而变大，这是因为ε＞an-a，能够清楚的进行运算，所以N、ε二者取值非固定，在探寻N值的过程中，如果明确满足定义条件的N，就能够取代为任何自然数n（n＞N）。然而无法轻松地获得N的取值，这就需要借助适当放大法进行运算，不等式ε＞an -a可能会相对烦琐，所以不能简单地得到n，这就需要ε＞an -a这一对绝对值不等式进行适当放大处理，获得：an -a

（二）函数极限

对于数列极限的概念，假设[a,+∞)中定义函数是f，定数为A，且任意正数ε>0，则有正数M（≥a），满足x>M的情况下，f（x）-A <ε成立，那么在x向+∞ 趋近时，函数f极限就是A，表示为f（x）→A（x→+∞），也可以写成lim x→+∞ f（x）=A 。针对数列an → →、函数f向+∞趋近二者的极限定义类似，由于二者自变数的改变规律一致，为n→+∞和x→+∞，仅在自变量改变形态方面有所差异。自变数x在函数f（x）内，取值范围是区间[a,+∞）下任意实数，续地增大；但是自变数n在数列an → →内，取值范围为所有正整数，离散地无限增大。这就表示，正整数N是数列极限的核心所在，正数M为函数极限f（x）→A（x→+∞）进行证明的重点。

（三）一元函数极限

对于一元函数极限的概念，假定点x0 处，函数f（x）任意空心领域内U°（x0；δ′）存在定义，且定数为A，任意ε>0时，具有正数δ（<δ′），满足0

针对数列极限进行进一步的延伸应用就能够获得函数极限，函数极限的典型就是数列极限，共同点在于极限针对的是自变量ε，数列极限内存在的因变量N，基于函数极限内写作δ，而在函数极限内ε是δ的基础所在，通常δ会因为ε的不断变小而出现有所减小的变化[3]。数理极限主要针对n向+∞趋近时数列值的改变趋势进行分析，但是函数极限则对x→-∞、x→+∞、x→x0、x→x-0及x→x+0时，函数值改变趋势进行研究。因此，函数极限、数列极限具有一致性，明确可变性δ的值就能够借助正数（＜δ）进行取代，从而找到函数极限的解。