转动惯量测量研究的进展及展望

王小三 刘云平 倪怀生 张 宁

(1.北京航天计量测试技术研究所，北京 100076；2．上海商用航空发动机有限责任公司，上海 200000)

1 引 言

转动惯量是刚体转动惯性的度量，是刚体绕定轴转动时的惯性量，其重要性等同于平动物体的质量。几乎所有绕定轴转动或做平面运动的刚体的运动定律均与转动惯量紧密相关，关于转动惯量测量的研究是航空航天强国的研究热点[1～10]，多年以来取得了较好的研究成果。从测量方法来看，按测量准确度从高到低以次为：扭摆法、落体法、三线摆法、复摆法、单线扭摆法和质量线法[13]。从测量适用性来看，复摆法不适用于较大物体，且该方法需要事先精确测量物体的质心[14]；落体法和单线摆法适用于陀螺转子、螺旋桨、齿轮、马达转子等绕轴线对称分布的构件[15]；三线摆法和扭摆法均可对外形不规则物体进行测量[12,15]；质量线法的理论基础复杂，测试精度较难保证，试验重复性较差，对试验人员要求较高,较难应用[16]。从国内外测量水平来看，美国空间电子公司、NASA、加拿大航空署等借助气浮球轴承，使用扭摆法研制了测量准确度达到0.1%FS的转动惯量测量设备；哈尔滨工业大学借助气浮轴承，使用扭摆法研制了测量准确度达到0.15%FS的转动惯量测量设备；西北工大、南京理工大学、郑州工程机械研究所等借助机械转台，使用扭摆法研制了测量准确度达到0.3%的转动惯量测量设备[17，18]。各类转动惯量的技术指标如表1所示[1，8]。

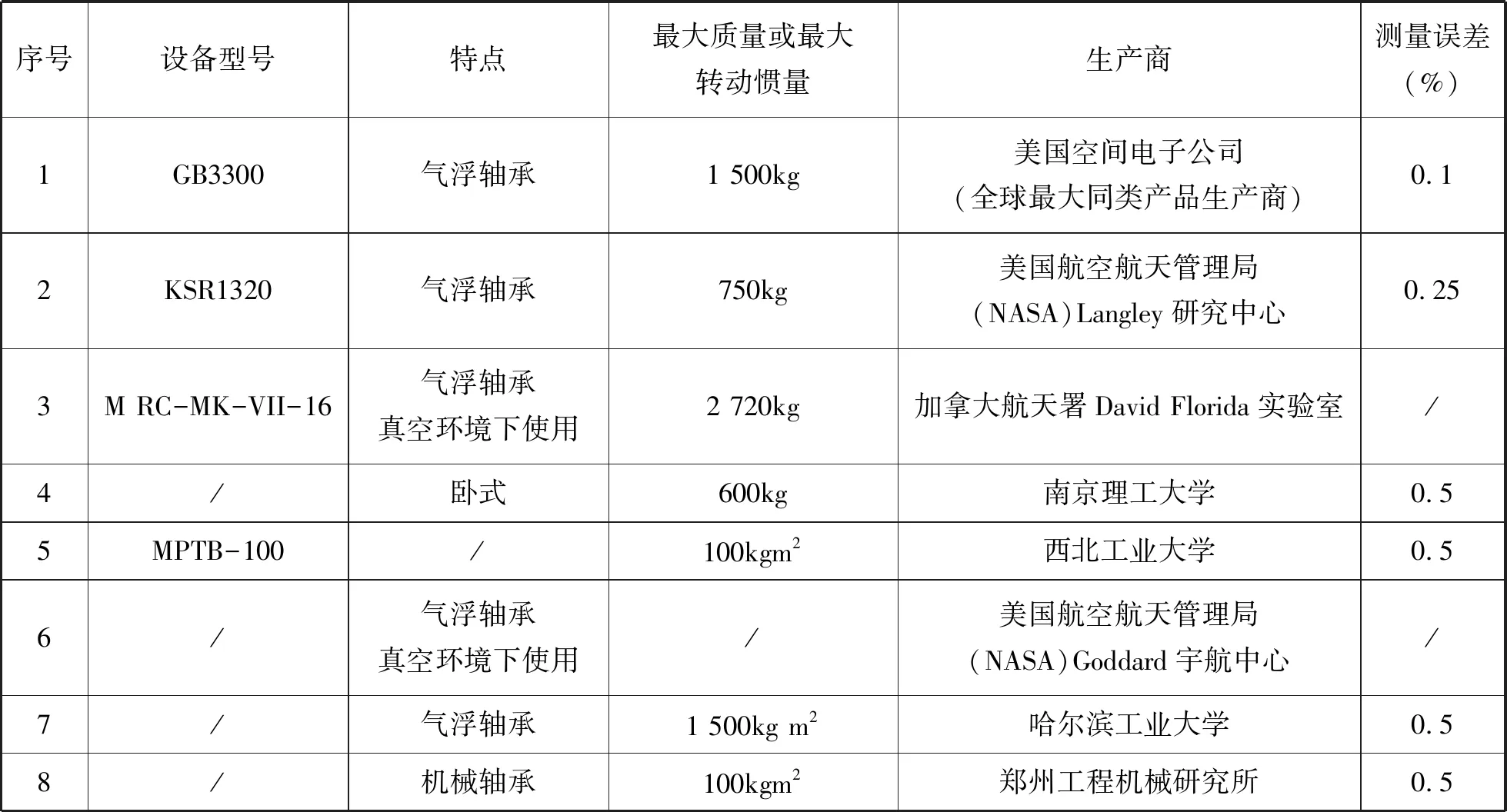
表1 扭摆法测量装置及精度Tab.1 Measuring device and precision by torsion pendulum method

2 转动惯量测量研究情况及成果

转动惯量是物体转动惯性的度量，测量原理及方法较多，下面重点介绍扭摆法、落体法、三线摆法等当前应用较多的方法。

2.1 扭摆法测量原理及其优缺点分析

2.1.1 测量原理

如图1所示，采用气浮或机械轴承，构建可绕定轴转动的扭摆系统，通过刚性连接，赋予扭摆系统刚度，测量时，通过主动驱动，使扭摆系统偏离平衡位置后释放，扭摆系统做正弦扭摆，测量扭摆周期，通过公式(1)计算待测物体转动惯量的测量方法为扭摆法。

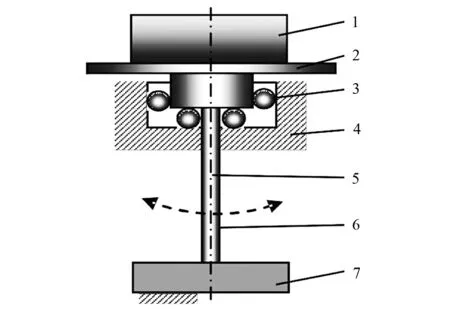
1-被测对象；2-测量平台；3-气浮或机械轴承；4-机架；5-定轴；6-扭杆；7-驱动与刹车机构。图1 扭摆法转动惯量测量原理示意图Fig.1 Principle of torsion pendulum method

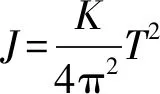
(1)

式中：J——物体对于扭摆转轴的转动惯量，kgm2；K——与扭摆系统扭杆刚度有关的一个常量；T——摆动周期，s。

2.1.2 优缺点分析

扭摆法是当前最为主流的转动惯量测量方法，具有以下优点：

a)测量准确度高。这种方法最高可达到0.1%的引用误差；

b)应用广泛。美国、德国等国的商业产品全部采用此种方法，我国的大部分设备采用此种方法；

c)测量效率较高。一次测量时间一般不超过4h；

d)承载能力突出。机械轴承的承载几乎没有上限，气浮轴承的承载上限约10t。

扭摆法的应用也有一定的局限性，表现在：

a)测量范围较小。该方法利用扭杆提供刚度构建机械扭摆系统，只有在一定的范围内扭杆刚度才能保持不变，而且该范围还必须与扭摆系统的适当扭摆频率基本保持一致，这个范围较小，也就是该方法所做出的测量设备，其测量范围较小；

b)测量溯源性较差。该方法以扭摆系统的简化理论模型为基础，通过测量刚度恒定的扭摆系统的扭摆周期测量转动惯量。一般来说，周期的测量没有问题，而系统的刚度及刚度恒定的要求在溯源上存在一定困难。

2.2 落体法测量原理及其优缺点分析[20～22]

2.2.1 测量原理

如图2所示，通过机械或气浮轴承，构建可绕定轴转动的转动系统，将质量、半径已知的圆形测量平台固定在转动系统上，并使测量平台的圆心过转轴，将吊线一端缠绕在圆盘上，一端通过等高的定滑轮悬挂一质量块，释放质量块后，转动系统将作匀角加速度运动，被测对象的转动惯量按公式(2)计算。

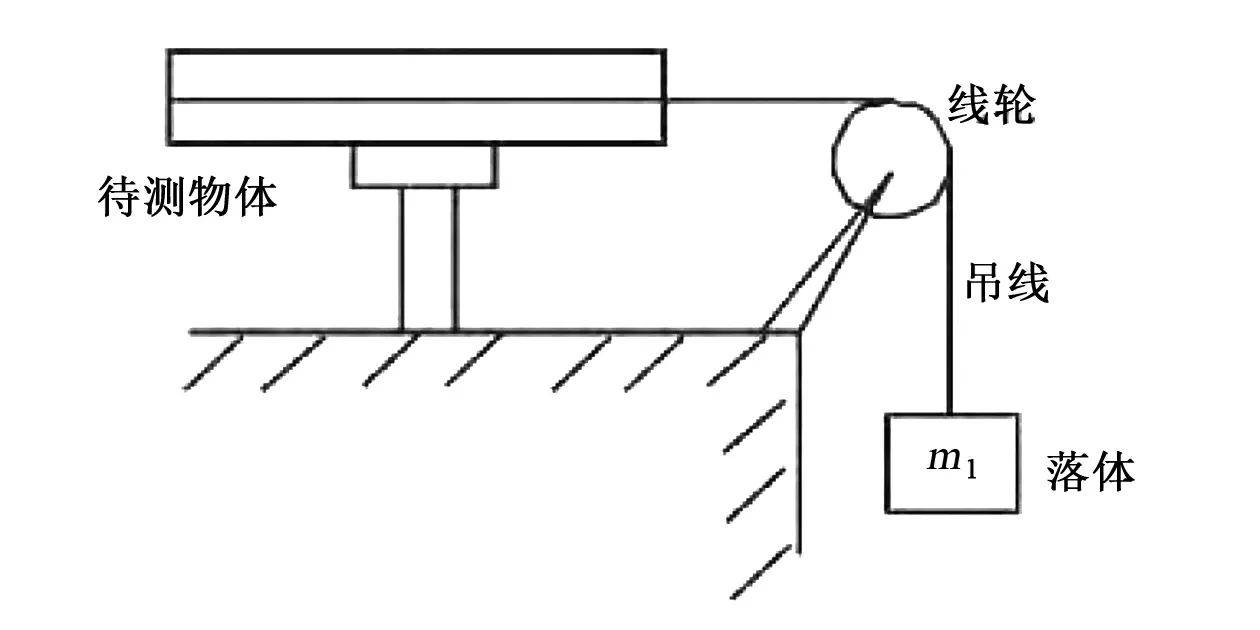
图2 落体法转动惯量测量原理示意图Fig.2 Principle of fall method

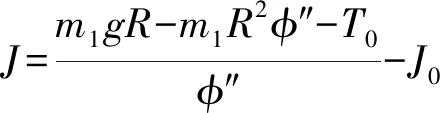
(2)

式中:m1——落体的质量，kg；R——圆形测量平台半径，m；φ″——角加速度，rad/s2；T0——摩擦力矩,Nm;J0——圆形测量平台转运惯量，kgm2。

2.2.2 优缺点分析

落体法在物理试验、教育教学中有较多应用，具有以下优点：

a)理论清晰。以刚体转动动力学为基本理论，与扭摆法的近似理论模型相比，具有理论清晰的突出优点；

b)适用特殊场合。有的电机，不允许或不便于取出其转子，无法知道其转动部分的质量和摩擦力矩。利用其他方法测其转动惯量无能为力，只有落体法可以胜任；

c)成本低廉。由于被测对象一般有自身的回转轴，可以因地制宜，不需要添置特殊的测量装置，成本低廉，因此本方法常用于物理试验、教育教学中。

落体法的应用也有一定的局限性，表现在：

a)测量空间要求较大。在实际测量时，理论上被测对象一直呈匀角加速运动，因此，准确测量角加速度、轴承摩擦力矩及质量块的质量即可测得较高准确度的转动惯量，但实际上轴承摩擦力矩较难准确测得而且不恒定，物体的转动并非匀角加速度，只能利用较大的运动空间来测出平均的角加速度，因此测量空间要求大;

b)实际测量准确度较低。由于测量过程中，所测得的角加速度用平均值表征，而平均值对应的设计值的波动性一般较大，因此，实际测量的准确度较低。

2.3 三线摆法测量原理及其优缺点分析[23～25]

2.3.1 测量原理

如图3所示, 当三线摆的下圆盘以oo′为轴转过一个角度时，由于悬线张力的作用, 将使下圆盘在一确定的平衡位置左右往复扭动, 即做扭摆运动。 若摆角很小, 则可视此扭动为角谐振动。此时，公式(3)成立。

(3)

式中：J′——被测对象绕oo′旋转的转动惯量，kgm2；m0——被测对象质量，kg；R′——下悬线节点距离转轴距离，m；r——上悬线节点距离转轴距离，m；l——悬线长度，m。

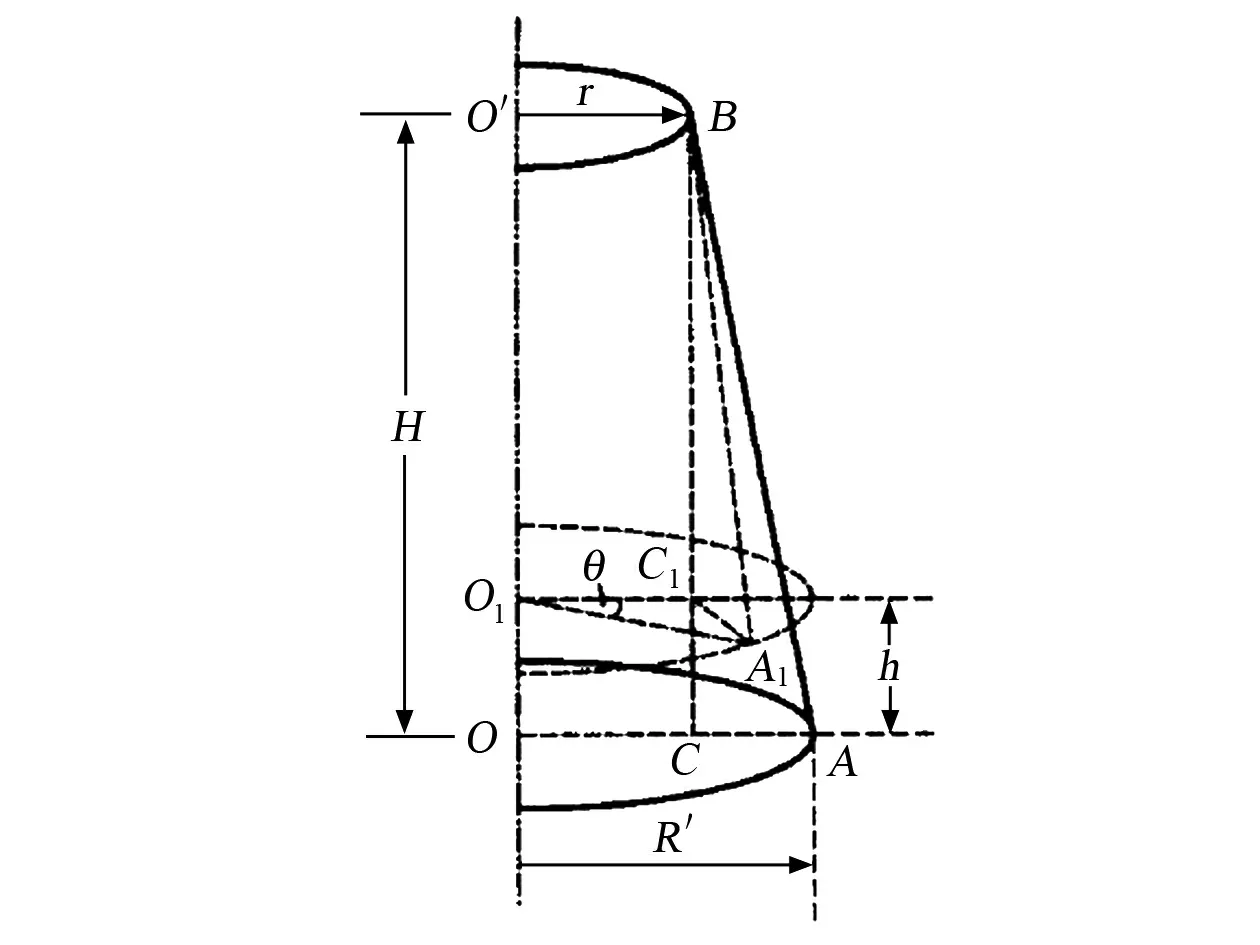
图3 三线摆法转动惯量测量原理示意图Fig.3 Principle of three wire pendulum method

2.3.2 优缺点分析

三线摆法是应用较多的转动惯量测量方法，具有以下优点：

a)结构简单。为了测量被测对象，只需在空间上固定一个上圆盘，在上圆盘上悬挂三根线，即可对下圆盘或置于其上的被测对象的转动惯量进行测量；

b)操作简便。悬挂后，一般用手即可驱动被测对象扭摆，完成测量，操作十分简便。

三线摆法的应用也有一定的局限性，具有以下优点：

a)测量准确度较低。该方法在实际操作过程中，容易出现平动和转动的耦合，影响测量准确度；而且，该方法一般假定悬挂的三线为轻质(质量为0)，而实际情况下，由于被测对象的质量影响，三线的质量一般不能忽略，这也导致测量准确度较低；

b)等效条件较难满足。用三线摆测量转动惯量，有一定的先决条件，如扭摆角度小于6°，扭摆阻尼的影响，以及被测对象质心与下圆盘之间的位置关系等等。

3 新型转动惯量测量测量方法及装置

2015年，北京航天计量测试技术研究所研究人员提出了一种新的转动惯量测量方法，该方法通过主动控制气浮转台作正弦扭摆，实时测量扭摆的角加速度和扭摆的驱动力矩，完成扭摆转台上刚体的转动惯量测量，取得了较好的效果。

3.1 测量原理

对于按一定频率和幅值的正弦运动，不考虑风阻及摩擦阻力的影响，可以根据公式(4)得到扭矩与角加速度的关系。

M(t)=J·a(t)

(4)

式中：M(t)——对转轴的力矩时域函数，Nm；a(t)——对转轴的角加速度时域函数，rad/s2。

3.2 测量设备

2016年9月，对该测量设备进行实测，在1000kgm2和2200kgm2测量点附近，重复性达到0.006%。测量设备实物图如图4所示。

图4 新型转动惯量测量设备Fig.4 A new type MOI device

3.3 优缺点分析

本方法是落体法和扭摆法的综合，具有以下优点：

a)理论清晰。以转动刚体的力学理论为基础，将转动惯量测量转化为便于测量的力矩及角加速度测量；

b)测量准确。测量重复性达到0.006%，这为提升测量设备的测量准确度奠定了良好基础，通过研究转动惯量校准技术，可望将该类测量设备的测量准确度由当前国际上最高的0.1%提升至0.01%；

c)安全可靠。在测量过程中，可根据被测对象的实际情况，合理调整扭摆的幅值及频率，以得到期望中的角加速度，可根据被测对象的特点进行操作，对被测对象来说，提供了安全选项。

本方法作为一种全新的测量方法，在一些方面仍有较大的提升空间：

a)理论简单，实际复杂。从测量原理来说，非常简单，但要构建一个宽测量范围的转动惯量测量系统，控制系统硬件的设计及选型、控制算法的设计、控制参数的调整等等，都比较复杂，有待简化；

b)结构简单，成本高昂。从结构上来说，非常简单，但要构建一个高准确度的转动惯量测量系统，主动控制系统的控制准确度、力矩测量系统的测量准确度、角加速度测量系统的测量准确度等等，都需要投入远远高于传统转动惯量测量设备的经费，成本太高，有待优化。

4 结束语

提升转动惯量测量准确度的研究是相关领域的重点和热点。从实际情况来看，在测量原理既定的情况下，通过动力学模型分析、考虑空气阻尼等影响来提升测量结果的准确度的研究目前陷入了瓶颈，而考虑空气阻尼的试验由于涉及到了大型真空舱等试验条件，成本很高。

由于高准确度转动惯量测量多用于国防工业，收集到的国外有关的资料中，多与原理相关，而技术细节极少。北京航天计量测试技术研究所研制的新型转动惯量测量设备，具有较高的应用价值，通过优化和简化，应用于工程实践，将可使我国的转动惯量测量能力得到较大幅度的提升。