绝对重力仪落体光心质心距调校方法研究

范 锋, 杨佩玺, 王启宇, 冯金扬, 要佳敏, 胡 若, 吴书清

(1.河北工程大学 数理科学与工程学院，河北 邯郸 056038； 2.中国计量科学研究院，北京 100029；3.国家市场监管总局 时间频率与重力计量基准重点实验室，北京 100029)

1 引 言

激光干涉式绝对重力仪采用激光干涉法测量落体在真空中自由下落的加速度。落体中内嵌1个角锥棱镜,测量时,通过激光干涉仪精确地测量真空腔中落体的下落位移与时间关系[3]。激光干涉式绝对重力仪测量的不确定度可以达到μGal量级(1 Gal=1 cm/s2)[3]。在绝对重力仪测量过程中,重力作用于落体的质量中心(简称质心,center of mass,COM),而干涉仪测量落体中角锥棱镜光学中心(简称光心, optical center,OC)的位移,由于落体加工和定位精度的限制,导致落体的光心与质心不完全重合,因此当落体在下落过程中发生旋转时,就会产生重力测值误差[6]。落体光心和质心的距离可分为垂直于重力方向的水平偏移量和沿重力方向的竖直偏移量,落体采用轴对称结构设计,在落体自由下落过程中,与竖直偏移量相比,水平偏移量很小,可以忽略不计。落体旋转误差作为绝对重力仪主要的不确定度来源,是影响其测量准确性和稳定性的重要因素[9]。

Hanada等采用旋转法调校落体[10],将落体放在1个旋转转盘上,通过高速旋转转盘,将质心调至旋转轴上,同时用迈克尔逊干涉仪测量经过落体反射的光程长度的变化,并通过计算1个周期内产生的条纹数来测量光心与旋转轴之间的距离。当条纹数最小时,认为光心与旋转轴重合,该方法的测量不确定度可达到50 μm。Germak等在此方法的基础上做了改进[11],用空气轴承将落体固定在旋转台上,通过迈克尔逊干涉仪将落体的光心调到水平旋转轴上,其测量结果的不确定度可达25 μm,但是由于旋转台本身并不是绝对平衡,且调校灵敏度很大程度上取决于空气轴承的摩擦力,因此会引入测量误差。Rothleitner等用三坐标机器测量光心位置、平衡机测量质心[12],使得两心间距的不确定度优于25 μm,当落体的旋转角速度为0.01 rad/s时,落体旋转引入的重力测量不确定度为0.7 μGal。但该方法属于接触式测量,测量时间长且设备搭建比较复杂。Niebauer等提出了利用扭力线悬挂落体的扭摆法[13],利用正交干涉仪测量了光心在扭转模式下沿干涉仪测量方向的位移。扭转模态的二次谐波振幅与质心和光心在重力方向上的偏移量成正比。通过调整质心螺母,使扭转模式的二次谐波振幅最小化。质心会围绕扭力线和下落体之间的悬挂点旋转到扭力线的延伸线上,从而完成对光心和质心距的调校。余烨等在扭摆法的基础上考虑了落体扭转和摆动模态等因素的影响[14],并进行了优化,通过理论分析,得到落体质心与光心之间距离的测量不确定度为1.4 μm。该方法虽然理论精度非常高,但对实验环境要求比较严格,其测量精度和正交干涉仪的分辨力有关,且耗时较长,装置和测量过程均较为复杂。由于上述方法较为复杂且只给出了光心质心距的测量结果,并未给出其在绝对重力仪实验验证的结果。

本文提出了一种基于落体悬吊的光心质心调校方法,该方法具有测量装置结构简单、调校简易高效的优点。基于该方法,搭建了一套落体调校装置,结合悬丝悬吊和落体的结构设计,利用高精度自准直仪监测落体的俯仰角,实现对落体光心质心的重合度调校。本文首先介绍了方法原理和装置,然后对装置的测量不确定度进行了评估,最终将落体放入NIM-3A型绝对重力仪中进行实验验证,并对实验结果进行了分析和讨论。

2 悬吊法原理及其装置搭建

2.1 落体光心质心距的影响机理

如图1所示,落体在下落过程中光心会绕质心以恒定的角速度旋转,从而引入光程的测量误差,其下落旋转过程中光程变化可表示为:

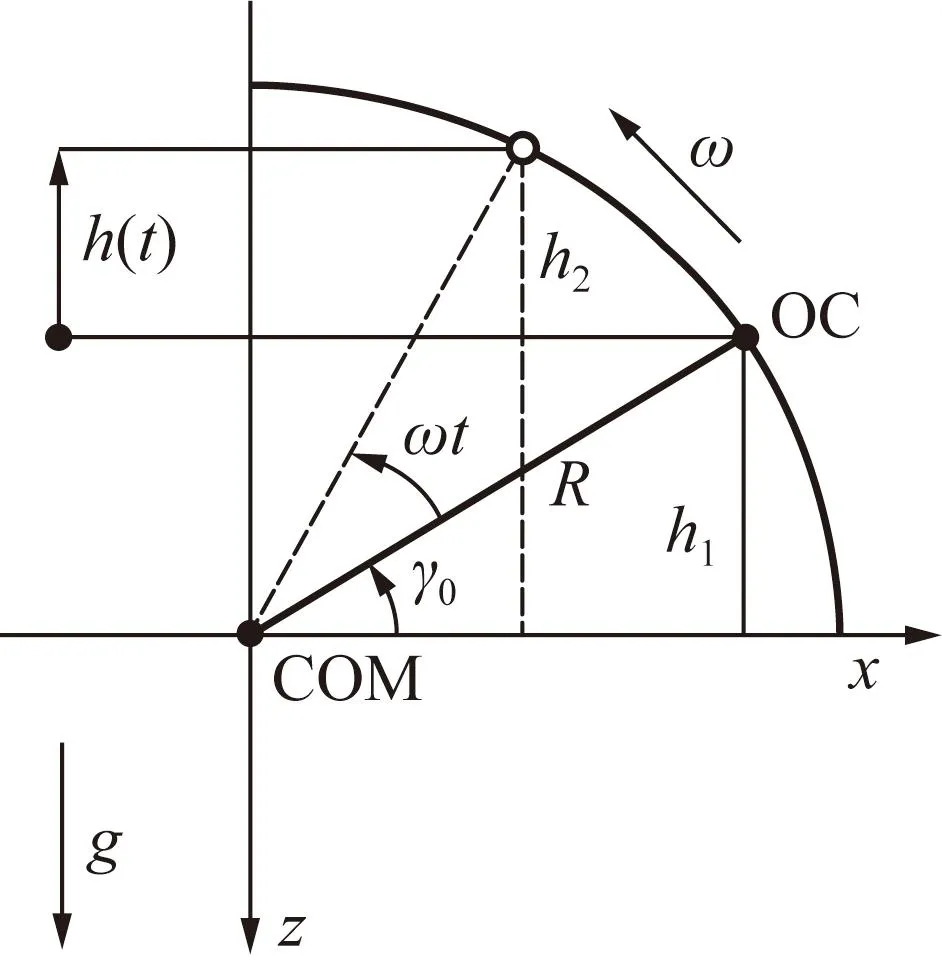
图1 落体干扰机理示意图Fig.1 Schematic diagram of falling body interference

h(t)=h2-h1=Rsin(γ0+ωt)-Rsinγ0

(1)

产生的重力值干扰项为:

Δg=Rω2sin(γ0+ωt)

(2)

式中:R为落体的光心质心间距;ω为旋转角速度;γ0为初始时刻光心与质心所在直线与水平面的夹角。

由于落体下落时间短,引起的偏转角度ωt很小,且当γ0为90°或270°时,R达到最大值Rmax,故式(2)可简化为:

Δg=ω2Rmax

(3)

在实际应用中,可通过最小化落体的光心质心间距来减小该项引入的误差。例如在FG5型绝对重力仪中[15],落体的光心质心间距调校到25 μm,通过机械精调使得落体的旋转角速度控制在0.01 rad/s,此时引入的重力测量不确定度可降低到0.25 μGal。随着落体支撑点的磨损和释放机构轴承的松动,落体会加剧旋转,在极端条件下,角速度会达到0.1 rad/s,则此时会引入25 μGal的旋转误差。因此,落体的光心质心距是1个重要的误差来源。

2.2 悬吊法原理

悬吊法调校落体光心质心距的原理如图2所示。落体采用轴对称设计,其中角锥棱镜的光心在落体的外圆线处,并将悬丝固定在该外圆线上的悬吊点处。当落体被悬吊后,若落体的光心和质心重合,则此时落体处于水平悬吊状态,如图2(a)所示;当落体的质心和光心不重合时,由于质心不在悬丝所在的轴线上,在重力作用下落体会发生转动,如图2(b)所示。同时假设自准直仪输出的光束(即入射光)严格处于水平方向,此时入射光与落体中角锥棱镜的法线方向之间的夹角即为悬吊状态下的俯仰角α。通过调节质心螺母对落体的质心位置进行调节,直至落体在悬吊状态下处于水平姿态,此时入射光垂直入射落体角锥棱镜表面,反射光沿原光路反射回自准直仪,则可通过自准直仪测量的俯仰角,将质心调节至与光心重合。此时质心移动的距离与α的关系为:

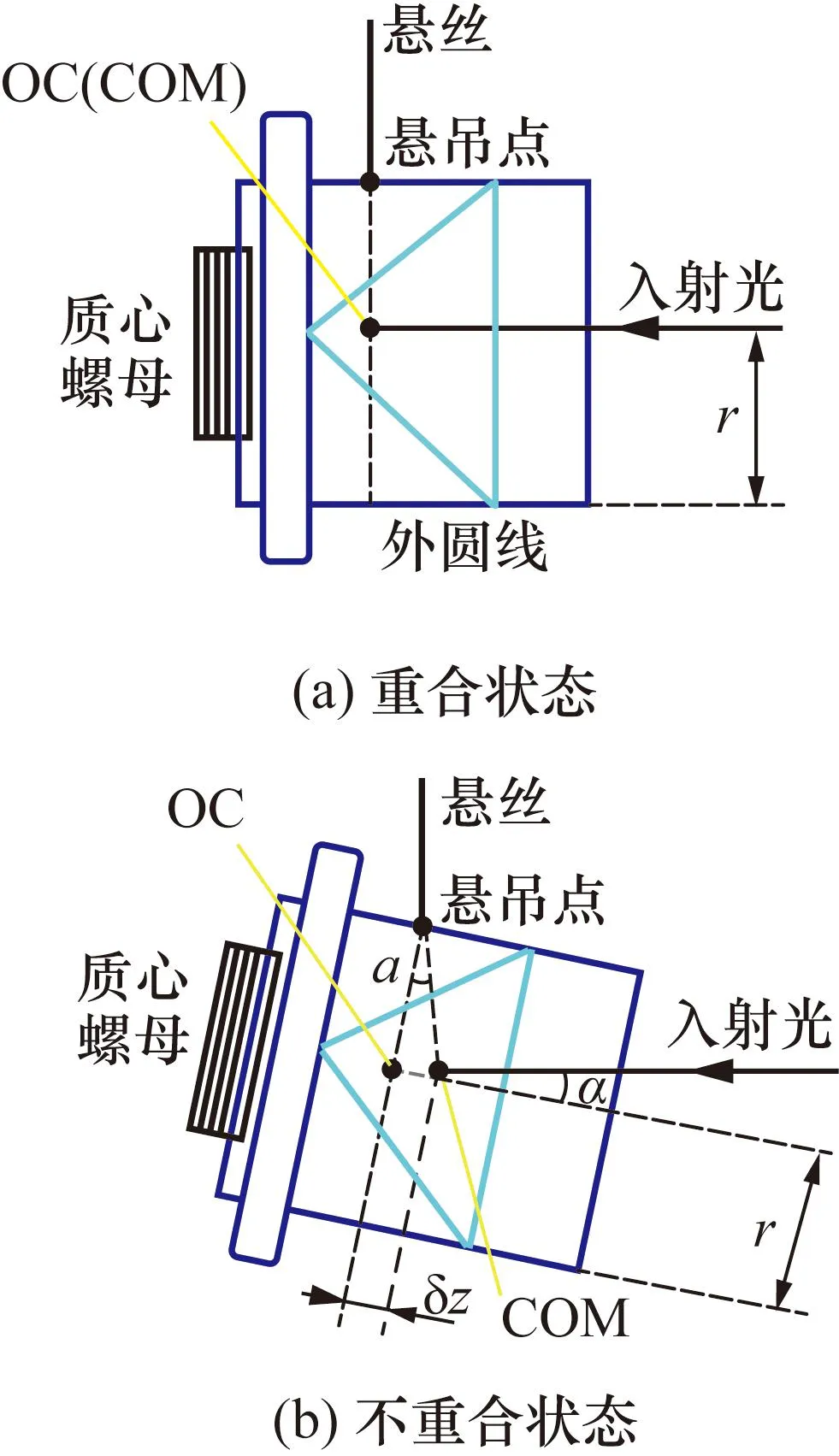
图2 悬吊法原理示意图Fig.2 Schematic diagram of the suspension method

(4)

式中:α为自准直仪监测的俯仰角;δz为光心和质心的间距;r为落体的底面半径。

2.3 悬吊法装置搭建

本文研究的调校装置主要由落体悬吊装置和高精度自准直仪组成。落体的质心螺母表面设计有可调节刻度,当质心螺母转动10°时,对应于落体质心的位置理论改变量为1.8 μm,这种落体结构设计具有较高的调校灵敏度。如图3所示,测量时以落体为参照物,光心相对于悬吊点的位置不变,此时角锥棱镜光心在悬丝轴线上。当落体处于水平悬吊状态时,该参考系的y轴与悬吊下落体的悬丝一致,z轴与自准直仪的测量光平行,x轴为与测量光垂直的水平轴。

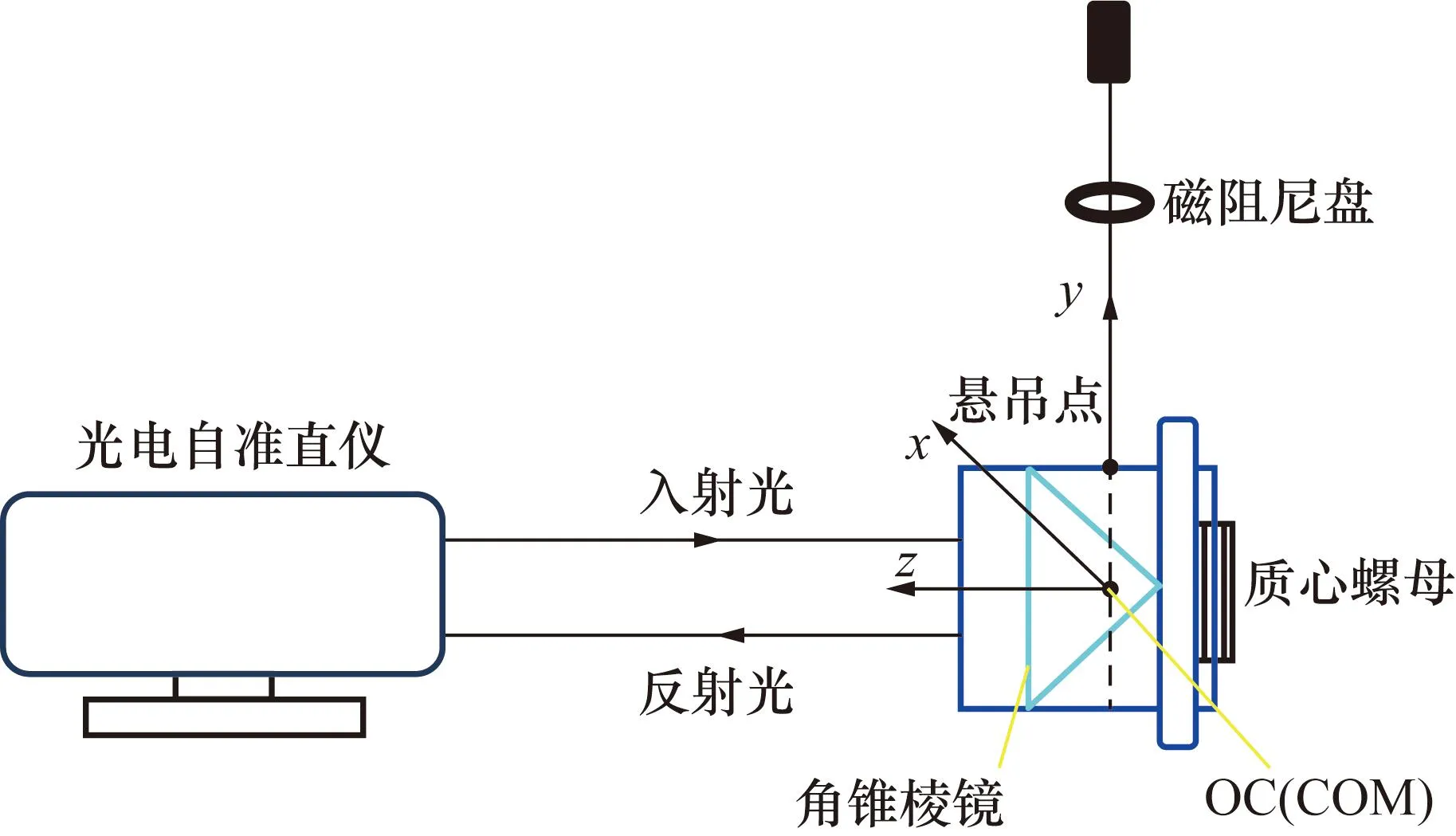
图3 悬吊装置示意图Fig.3 Schematic diagram of the suspension device

为了保证悬吊法装置测量的准确度,因此,在测量之前需先对自准直仪进行初始调节校准,将其主光轴的输出光方向调整到水平方向。测量时,使落体在悬丝的牵引下处于自由摆动状态,使得落体在水平位置做小角度扭转,自准直仪的入射光完全直射在角锥棱镜的底面上,并且使用磁阻尼装置对落体摆动进行快速衰减,使得落体尽快进入准静止状态。同时,在软件视窗内观察反射十字光的位置,调节落体质心螺母将反射光调至与自准直仪光源的十字光重合。由OptiAngle软件实时观测俯仰角,其测量界面如图4所示,界面右上角可以得到落体角锥棱镜的反射光与自准直仪十字光存在的夹角为2.77″,因此可知此时落体已处于水平悬吊状态,其质心与光心已经基本重合。

图4 俯仰角监测Fig.4 Pitch angle monitoring

3 测量不确定度分析

3.1 测量重复性引入的不确定度

根据本文所提方法,在相同实验条件下,将调校完成的落体进行10次重复悬吊,由俯仰角监测得到的落体光心质心间距δz的实验数据如表1所示。

表1 重复性实验数据Tab.1 Sheet of Repeatability Experiment Data

由于每次重复悬吊落体存在人为操作误差,导致重复悬吊位置不唯一,从而产生一定的测量误差。因此采用贝塞尔公式法对测量可重复性引入的不确定度uA进行评估,实验标准差由式(5)计算:

(5)

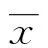
实际测量以3次测量每次测量10个结果均值作为估计值,计算得到测量重复性引入的不确定度分量uA:

(6)

3.2 系统误差项引入的不确定度

1) 落体结构误差

如图5所示,考虑到由于机械加工精度的影响,落体在装配时理论上光心所在的外圆线与角锥棱镜光心的实际位置存在测量偏差,悬吊法调校完成后,实际的悬吊位置与光心会偏离距离Δl。因此要实现正确的调校,需要根据落体加工误差的正负再次调节质心螺母进行修正, 修正量为Δl。

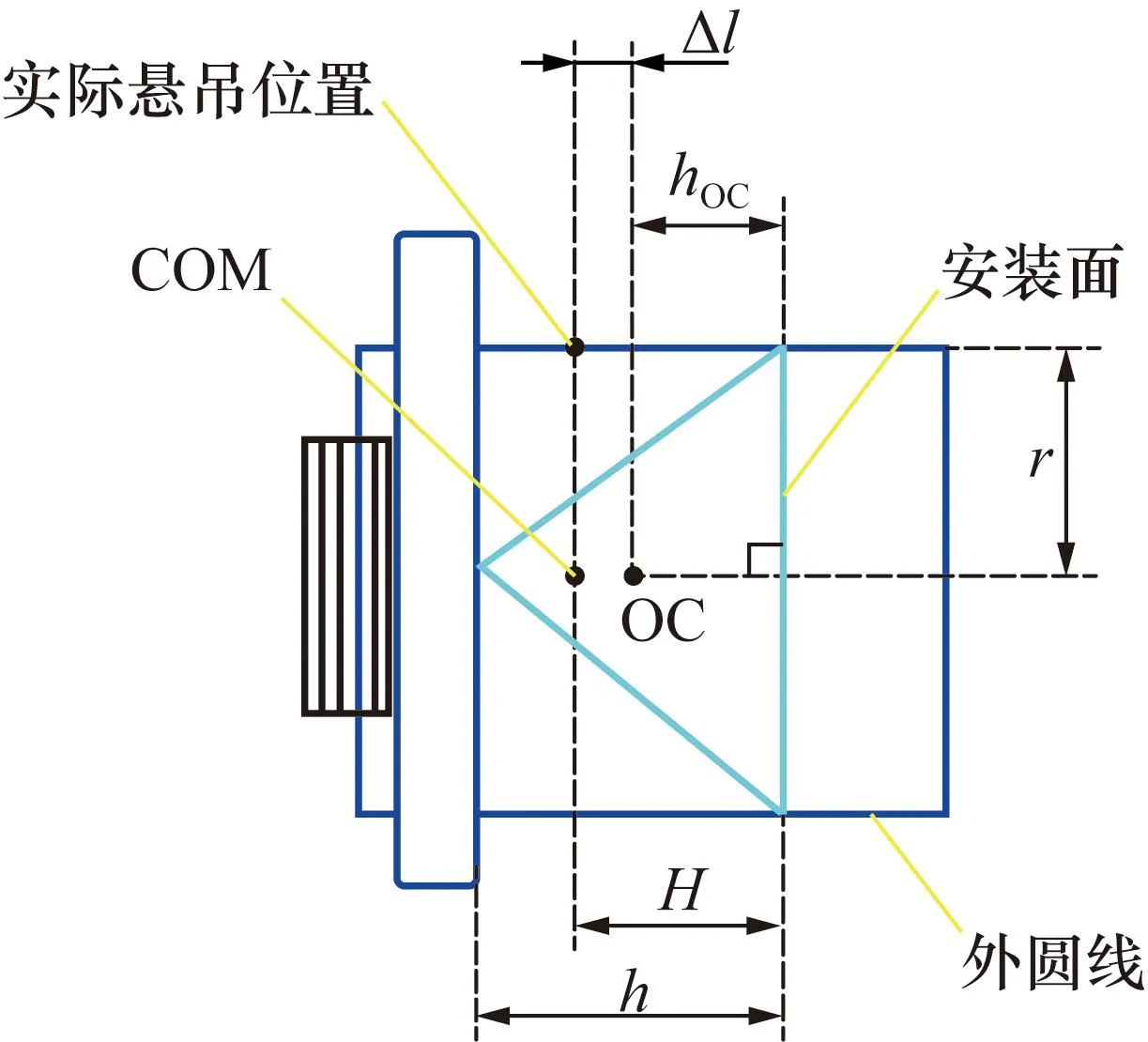
图5 误差修正示意图Fig.5 Schematic diagram of error correction

Δl=|H-hOC|

(7)

式中:H为角锥棱镜的安装面到悬吊点外圆线的高度;hOC为角锥棱镜光心的实际高度。

由于落体选用的角锥棱镜为实心角锥棱镜,考虑到其在空气中的折射率出厂标定为n=1.515 09,则实际光心位置hOC可等效为:

hOC=h/n

(8)

式中:h为角锥棱镜顶端到底部端面的垂直距离。

因此落体装配时需要准确测量H和h。实验采用高准确度自动影像测量系统的球头探针模式(接触式,型号为DT5040M/A,测量准确度为0.003 mm)测量。实验共测量同一批次5个落体,每个分别测量5次并取平均值,最后得到H的均值及标准偏差,结果如表2所示。

表2 H测量结果Tab.2 Result of H measurement mm

由表2所示的测量结果可知,得到该项引入的δz测量不确定u1=8.79 μm。

实验采用测量分辨力为±0.002 mm影像仪分别测量5个落体对应的5个角锥棱镜在三维空间内棱镜顶端到底面端面的垂直距离h,每个重复测量5次,结果如表3所示。

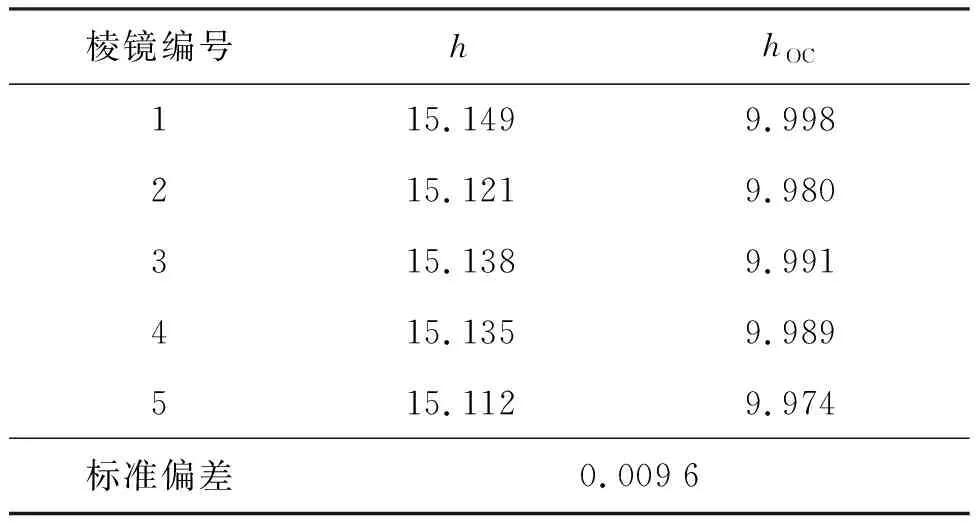
表3 光心位置测量结果Tab.3 Position measurement results of OC mm

由表3所示的测量结果,可以得到由光心测量引入的δz测量不确定度u2=9.68 μm。

2) 悬丝悬吊误差

考虑到悬丝与落体之间属于金属接触,当落体处于水平悬吊状态时,在重力作用下悬丝与落体之间会产生摩擦力。由于落体实际质心位置与悬吊点并不一致,使得原本落体在水平位置的小角度偏移会被悬丝摩擦力平衡,从而对实际的光心质心间距产生测量误差。如图6所示,悬丝在重力作用下发生微小的拉伸形变,则落体此时所受应力F可以等效为式(9)所示形式。

图6 落体受摩擦力示意图Fig.6 Schematic diagram of the friction force on falling body

(9)

式中:S为悬丝的横截面积;E为悬丝的杨氏模量;K为悬丝的原长;ΔK为悬丝的拉伸量。

如图6所示,以水平面为参考面,落体在y轴上的受力,有:

Fsinθ=fcosθ

(10)

在z轴上的受力有:

mg=Fcosθ+fsinθ

(11)

式中θ为落体实际与水平面的夹角;m为落体的质量;f为悬丝与落体间的摩擦力。

为了减小悬丝摩擦力引入的误差,考虑到悬丝的物理特性,实验选用的悬丝材料为摩擦系数较小且刚性较强的钨丝,其长度为60 mm,直径为20 μm,落体整体的质量为56 g。由式(9)～式(11)评估出落体与水平面的偏转角θ可达到0.8°,则由悬丝摩擦力引入的δz测量不确定度u3=12.57 μm。

3) 自准直仪测量误差

实验使用的自准直仪TriAngle TA300-57,角度范围为±0.21°,测量分辨力为0.003″,测量准确度为±0.75″。由蒙特卡罗(Monte Carlo)法模拟评估得到,自准直仪引入的δz测量不确定度分量u4=0.01 μm。

3.3 合成标准不确定度

由于落体结构误差、光心位置误差、悬丝悬吊误差、测量仪器误差之间没有相关性,则悬吊法调校落体光心和质心距δz的合成标准不确定度为:

(12)

取置信因子k=2,扩展不确定度U为37.7 μm。

4 实验与结果

4.1 悬吊法分辨力测试

为验证第3节评估结果的准确性,将调校完成的落体通过多次调节质心螺母来改变其质心与光心的距离。质心螺母旋转1圈,质心理论改变量为64 μm。在调校过程中,依次将质心螺母旋进1圈,然后旋出0.5圈和1.5圈,结果如图7所示。

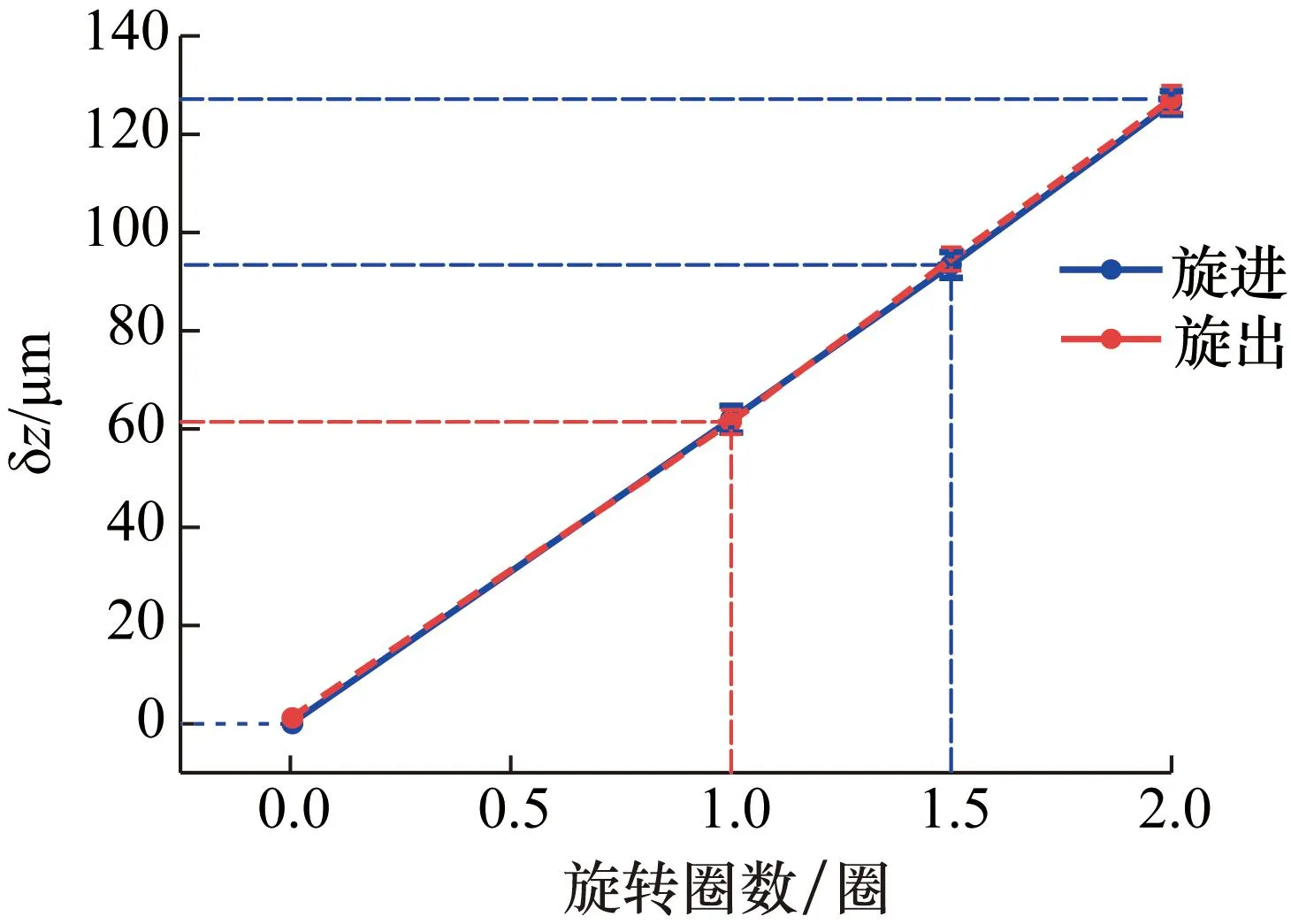
图7 调校分辨力Fig.7 Adjustment accuracy

每次改变质心螺母在落体中的位置所引起质心的理论变化与悬吊法实测变化如表4所示。由表4可以看出,通过调整质心螺母改变落体质心位置,得到实测值与理论改变量误差小于1.3 μm。

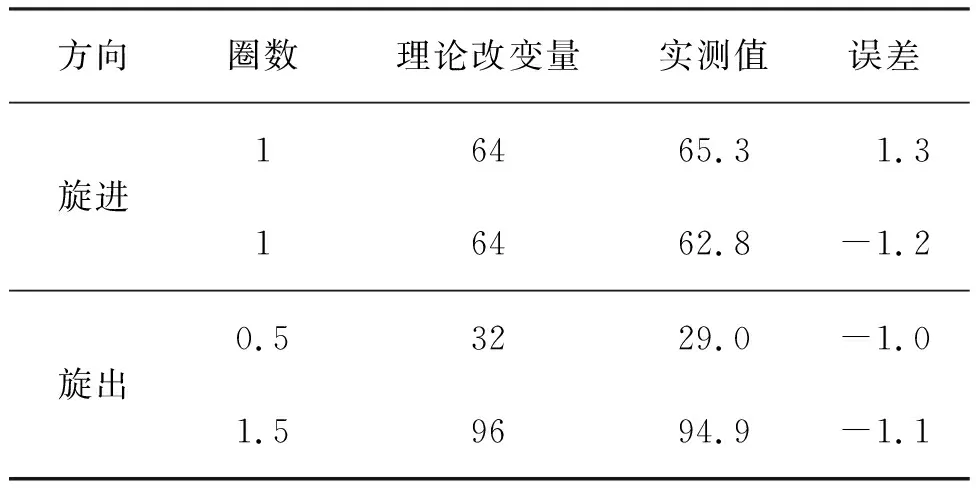
表4 δz调校数据表Tab.4 Adjustment datas of δz μm

4.2 绝对重力仪实验结果

为了进一步验证悬吊法调校落体光心质心距的准确性,在仅改变落体的条件下,分别将调校前后落体在NIM-3A型绝对重力仪上进行对比实验,并同步进行落体旋转角速度测量[16],以下为其中1个落体的实验结果,实验地点为中国计量科学研究院昌平院区重力基准实验室,该点位的重力参考值为9.801 226 446 Gal。

将调校前后的落体分别完成10组,每组40次,每组间隔40 min,总共400次下落测试实验。其中图8(a)为落体调校前后的重力值测量结果,可以看出调校后落体的重力测值的分散性显著减小,调校后落体重力测值的标准偏差从51 μGal减小到27 μGal。图8(b)为本次实验每组的测量结果(平均值)。实验结果表明,调校后落体重力测值的标准偏差优化到调校前的1/2。落体旋转角速度测量均值如表5所示,考虑到重力仪的测量不确定度,其实测值与参考值的差值Δg包含其它误差项,因此用Δg的最大值计算可得到δz的最大值,则由式(3)可以得到:调校前落体的光心质心距δz小于96.71 μm,调校后落体的光心质心距δz小于19.43 μm,实验结果满足第3.3节不确定度评估结果(k=2)。

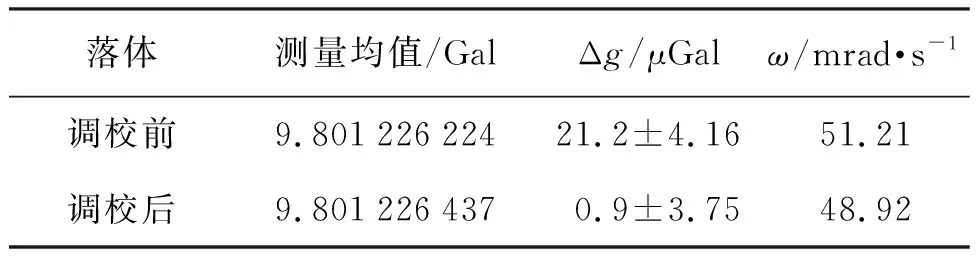
表5 测量结果Tab.5 Results of measurement

图8 落体调校前后重力测量对比结果Fig.8 Comparison results of before and after falling bodies adjustment in absolute gravimeter

4.3 讨论

由实验结果可知,悬吊法调校后落体的光心质心距虽然能满足NIM-3A型重力仪的正常使用需求,但是悬吊法的调校不确定度仍有优化空间。分析导致悬吊法的调校不确定度受限的原因可能是角锥棱镜加工及工艺处理过程中顶角的磨损,所以实际的棱镜高度hoc就会偏小,从而导致计算修正量Δl包含的误差不可控。

目前准确定位光心位置的方式和精度都存在局限性,因此,落体角锥棱镜光心的精确定位是个比较大的误差项。另一方面,经过评估得到悬丝的摩擦力为最大的不确定度分量,通过优化悬吊方式或更换更合适材料的悬丝减小摩擦,优化理论模型,可以再进一步减小悬吊法的调校不确定度。

5 结 论

落体光心质心距的精确调校对于提升NIM-3A型绝对重力仪的测量准确性和稳定性十分重要。本文设计了一种基于悬吊法的落体调校装置,实验结果表明:

1) 经过评估其调校落体的光心质心距的不确定度优于20 μm,并在NIM-3A型绝对重力仪中得到验证。若落体旋转角速度控制在0.02 rad/s以内,则调校后落体引入的重力测值不确定度优于1 μGal。

2) 悬吊法可以实现在简易环境下实现精确的质心调校,该方法具有测量装置构成简单、调校方式简易的优势,且落体光心质心距的调校精度满足NIM-3A型绝对重力仪的高精度测量需求。

此外,该方法还可以应用于多种同类重力仪的落体调校,为提升我国自主研发的自由落体式激光干涉绝对重力仪的测量不确定度水平及可靠性提供帮助。