落石冲击作用下钢-混凝土组合梁上砂垫层的耗能性能

罗 杰， 肖建春， 马克俭， 毛家意， 张 弘

(1. 贵州大学 空间结构研究中心, 贵阳 550003; 2. 中建四局第六建筑工程有限公司, 合肥 230011;3. 贵州省结构工程重点实验室, 贵阳 550003; 4. 贵阳市人民防空办公室, 贵阳 550001；5. 贵州建工集团第六建筑工程有限责任公司, 贵阳 550009)

钢-混凝土组合梁受到冲击时容易受到损伤。砂土是良好的能量耗散体，冲击作用下砂土颗粒之间发生强烈挤压和摩擦，延长了冲击时间，减小了传至下部结构的冲击力。在防护工程中经常采用砂土做缓冲垫层[1-4]。

为研究砂土在防护结构中的缓冲性能，一些学者进行了相关研究。Tam等对覆盖砂砾土的H型钢截面简支梁进行了冲击试验，分析了冲击能量传递路径，并阐明了砂砾土的缓冲机理[5]。裴向军等[6]对砂土覆盖下混凝土框架结构受滚石冲击进行数值计算，分析不同冲击能量下多组砂土垫层厚度组合的动力响应及耗能缓冲机理，得到了滚石冲击能量预估公式。这些研究只针对H型钢梁和钢筋混凝土梁的砂土垫层，未发现有学者进行钢-混凝土组合梁砂土垫层的耗能性能的研究。

本文采用试验和数值模拟来研究落石冲击冲击作用下钢-混凝土组合梁上覆盖砂土垫层的耗能性能。使用试验定性分析砂土的耗能作用；通过数值模型找出这类组合梁砂土垫层的冲击耗散能量与落体冲击能、垫层厚度之间的关系。

1 模型试验

1.1 试验模型

制作了6根相同尺寸的比例1∶4的钢-混凝土组合梁。钢梁长L=2 050 mm。钢筋混凝土面板厚度62.5 mm，混凝土强度等级C30，双向双层配筋，上、下层纵向钢筋φ4@80，横向钢筋φ4@110。焊接H型钢、焊接栓钉和其余试验用钢材均采用国标Q235钢。焊接H型钢截面尺寸150×125×5×8。焊接栓钉2M10@110，沿钢梁跨度均匀布置。钢筋混凝土试验基座上预埋16 mm厚钢板，在预埋板上焊接50 mm直径的钢棒模拟组合梁的铰支座。落体采用混凝土圆台，重mi=225 kg。垫层采用级配中砂。试件的正面图和侧面图如图1和图2所示。

图1 试验正面图 (mm)Fig.1 Front view of the test(mm)

图2 试验侧面图(mm)Fig.2 Side view of the test(mm)

试验选取落体高度和垫层厚度作为研究参数。通过钢丝绳来调整落体高度。钢丝绳与地锚之间用φ10钢筋连接，使用钢筋夹钳切断钢筋来释放落体。级配砂垫层位于组合梁跨中，用5 mm厚木板作砂垫层的外框，外框高度与砂垫层厚度相同。试验安排见表1。在钢筋混凝土面板的4个外角布置有防护砖柱，以防止试验中出现意外。防护砖柱与钢筋混凝土面板的间距20 mm。试验如图3所示。

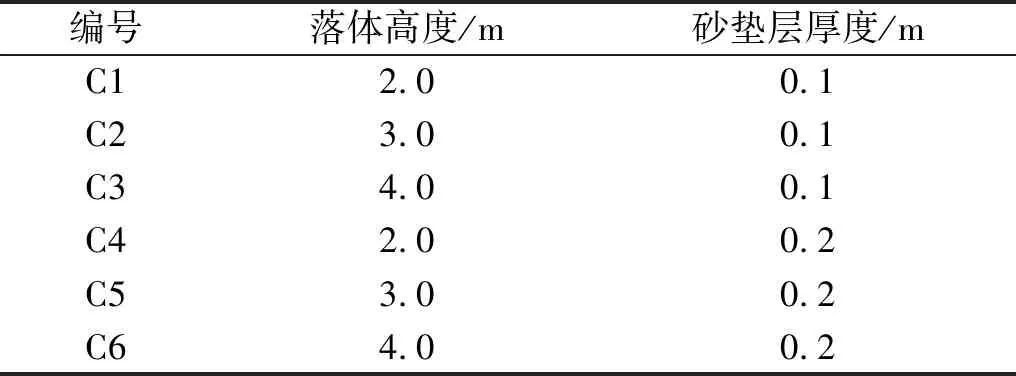
表1 试验模型Tab.1 Test model

图3 落体试验Fig.3 Drop hammer test

试验数据为试验过程中组合梁跨中的最大挠度，以及试验结束后钢筋混凝土面板的裂缝宽度。采用CF0550-400位移传感器与SDA-810C动态应变仪来读取组合梁跨中的最大挠度。通过ZP-CK103裂缝宽度观测仪测量混凝土板的裂缝宽度。该仪器放大倍数为60倍，裂缝宽度值测量范围为0～10 mm，可估读精度为0.001 mm。

1.2 试验结果

(1) 试验过程中组合梁跨中的最终位移。

读取试验过程中组合梁跨中的最终位移，如表2所示。可以看出，在相同砂土垫层厚度下，组合梁跨中最终位移差值与落锤冲击能成正相关。0.1 m厚的砂垫层对应的最终位移值高于0.2 m厚砂垫层对应值，比例大约为1.46～1.5。砂土垫层起到减小组合梁跨中最终位移的作用较为明显。

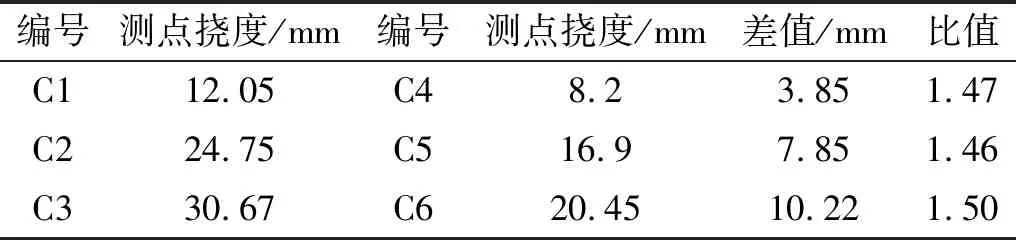
表2 测点挠度Tab.2 Deflection of the measuring point

(2) 钢筋混凝土面板的裂缝宽度。

试验结束后，清除覆盖的砂垫层，观察钢筋混凝土面板的裂缝。除了C4以外，其余5根梁钢筋混凝土面板的上表面均出现了横向和纵向的裂缝，纵向裂缝宽度大于横向裂缝宽度。测量裂缝数据见表3。

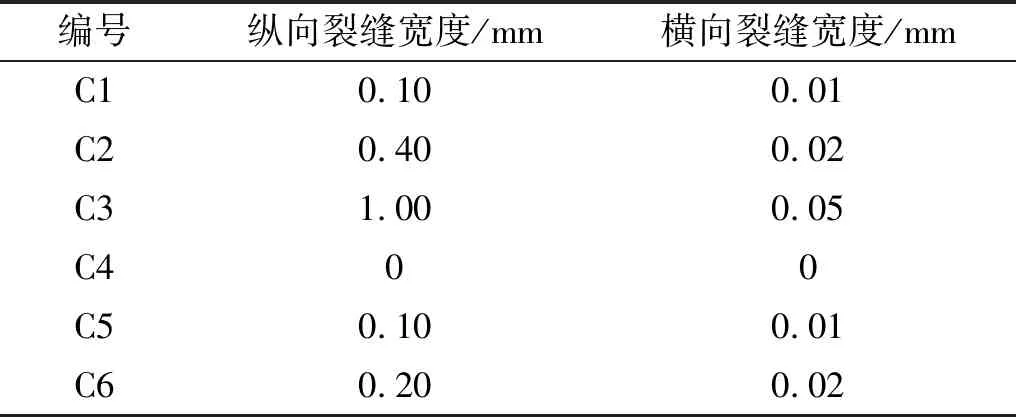
表3 裂缝最大宽度Tab.3 Maximum width of crack

最大纵向裂缝和横向裂缝均出现在C3。C3在跨中附近混凝土板面出现的横向裂缝最宽，其余5根梁的横向裂缝非常小。横向裂缝分布范围集中在跨中l/20的范围内。除C4外，其余5根梁混凝土板面沿H钢梁纵轴展开的裂缝长度均超过l/3，其中C2，C3沿梁贯通，如图4所示。除C4外，其余5根组合梁的侧向均出现沿H型钢边缘至混凝土板中央的斜向裂缝，如图5所示。

图4 C2混凝土板裂缝Fig.4 Crack in the concrete slab of C2

图5 C2混凝土板裂缝侧向图Fig.5 Side view of crack in the concrete slab of C2

冲击能量很大时才伴随出现横向裂缝。如砂垫层厚度不变，则纵向裂缝宽度随落体高度增大而增大。如落体高度相同，则纵向裂缝宽度随砂土垫层厚度增大而减小。说明冲击破坏形式与冲击能量的大小和砂垫层耗能强弱有关。砂土垫层可以控制组合梁中混凝土板裂缝的宽度且作用明显。

(3) 砂土现象分析。

在冲击作用下，落体在砂土中形成砂坑。落体周围的砂子有翻起并略高于原表面。组合梁受冲击后与木框暂时脱离，砂子之间产生的摩擦力和接触力导致少量砂子从四周侧向木框下流出。在冲击作用下，有部分砂土粒子形成飞溅现象。其中小部分射向木框外，如图6所示。这表明滑动摩擦耗能和飞溅等运动耗能为砂土在受冲击后的部分耗能现象。

图6 冲击后模型状态Fig.6 Model status after impact

2 理论分析

SPH-FEM(Smoothed Particle Hydrodynamics-Finite Element Method)方法不仅在处理大变形、自由表面等问题时具有明显的优势[7-10]，而且计算效率较SPH方法快[11]。因此SPH-FEM方法是处理冲击动力学问题的有效手段之一[12]。

采用SPH-FEM方法分析6组试验中落体的冲击力时程曲线、能量分配和跨中位移。并对25组以混凝土圆台的落体冲击能和级配中砂垫层的厚度作为研究参数的SPH-FEM模型进行回归分析得到砂土垫层的落体冲击能、砂土垫层厚度与能量耗散、最大冲击力之间的关系式。

2.1 材料模型

采用LS-DYNA建立SPH-FEM模型，如图7所示。钢梁、混凝土板、栓钉、混凝土台座、砖柱、木框架和落锤均采用实体单元，钢筋采用梁单元，砂土采用SPH粒子。

图7 SPH-FEM模型 (mm)Fig.7 SPH-FEM model(mm)

通过CONTRAINED_LAGRANGE_IN_SOLID来连接钢筋与混凝土板。混凝土板采用混凝土连续面盖帽模型[13]。模型考虑了材料的硬化、损伤以及率相关性，目前在混凝土低速冲击领域应用广泛，参数具体见表4。钢材采用等向随动强化模型和VonMises屈服准则，按Cowper-Symonds方式考虑应变率效应对材料屈服强度的影响，参数如表5所示。砖柱与木框采用弹性模型。木框的弹性模量、密度和泊松比分别为9×105MPa，400 kg/m3和0.2。砌体材料密度、弹性模量和泊松比分别为1 600 kg/m3，3.0×104MPa和0.2。混凝土台座和落体采用刚体模型，密度为2 500 kg/m3。

MAT_SOIL_AND_FORM模型较为适合用于砂土的研究。模型中砂的主要参数：密度1 800 kg/m3，剪切模量63.8 MPa，初始模量134 MPa，内摩擦角35°；砂土为干砂，含水率为0，因此表观黏聚力近似为0；二次曲线常数a0=a1=0，a2=0.3。理想弹塑性屈服函数为

(1)

式中：φ为偏塑性屈服函数；Sij为偏应力分量；A0，A1，A2为常数；P为压力。

表4 混凝土参数Tab.4 Parameters of concrete material

表5 钢材材料参数Tab.5 Parameters of steel material

2.2 边界处理和荷载

自动接触不需要人工干预。木框与砂土、混凝土板与砂土均采用自动点面接触来耦合[14]，落体与砂土的碰撞则采用点面接触。动摩擦因数均为0.3[15]。将SPH粒子定义为从节点，有限元单元为主面。钢梁上翼缘和混凝土板、栓钉和周围的混凝土采用自动面面接触，摩擦因数设定为0.5[16]。砖柱与混凝土板、钢梁下翼缘与钢棒设定为自动面面接触。对砖柱和台座底部施加固定约束。采用动力松弛的算法完成重力荷载所产生应力的初始化。

3 数值分析

3.1 冲击力分析

落体与砂土之间的冲击力时程曲线，如图8～图10所示。各组冲击力曲线快速增大至峰值随后降低，经过多个峰值后接近0。这表明落体通过多次与砂土碰撞起到了缓冲的作用。C1与C4的最大冲击力相差较多，而C3与C6相差最小。分析表明当砂土层厚度从0.1 m增加至0.2 m，落体与砂土之间的冲击力与落体的冲击能量增长成反相关。这说明当砂土垫层增幅厚度相同(砂土层厚度从0.1 m增加至0.2 m)，冲击能量越小(落体高度从4 m降低至2 m)，砂土起到缓冲冲击力的作用越明显。产生这种情况的主要原因是当冲击能量较大时，砂土垫层在极短时间内大幅度压缩，使得冲击更易受到垫层下方钢-混凝土组合梁的影响，相当于在减小垫层厚度的同时增大了垫层的有效刚度，很大程度上限制了砂土垫层发挥减小冲击力的作用。

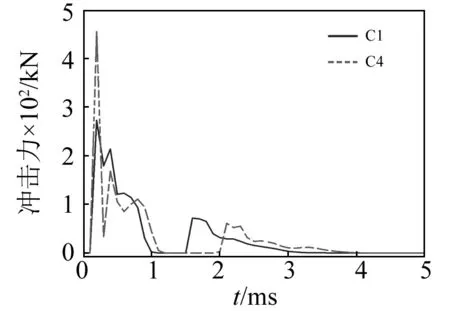
图8 C1与C4冲击力时程曲线Fig.8 Impact force-time history curve of C1 and C4

图9 C2与C5冲击力时程曲线Fig.9 Impact force-time history curve of C2 and C5

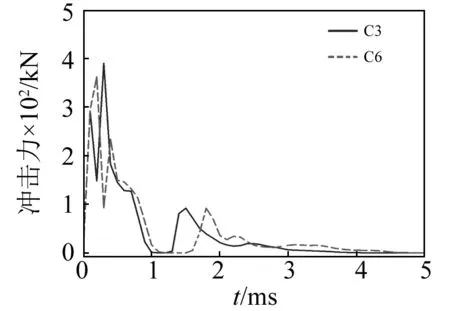
图10 C3与C6冲击力时程曲线Fig.10 Impact force-time history curve of C3 and C6

3.2 能量分布

图11为6组试验所对应的SPH-FEM模型砂土耗能时程图。砂土耗能曲线快速增大至峰值，然后趋于稳定。曲线均在增大后有微减。数值模拟未考虑落体在下降过程中空气摩擦等因素产生的能量损耗，系统的总能为落体的总势能。系统总能由砂土耗能、组合梁耗量、接触能、侵蚀能、沙漏能和人工黏性力能量损耗组成，如表6所示。表中砂土耗能与组合梁耗能中均包含侵蚀能。接触能与沙漏能均小于10%，模拟得到的砂土耗能较为准确。由人工黏性力引起的能量损耗等于总能减去其余四项能量，该值小于总能的5%。

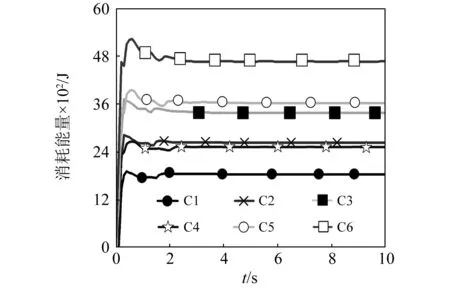
图11 砂土耗能时程图Fig.11 Dissipation energy-time history curve

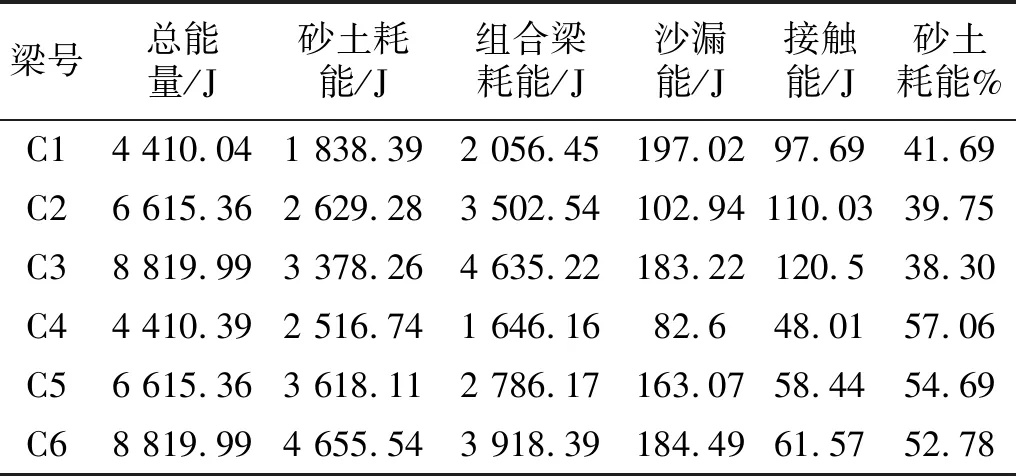
梁号总能量/J砂土耗能/J组合梁耗能/J沙漏能/J接触能/J砂土耗能%C14 410.041 838.392 056.45197.0297.6941.69C26 615.362 629.283 502.54102.94110.0339.75C38 819.993 378.264 635.22183.22120.538.30C44 410.392 516.741 646.1682.648.0157.06C56 615.363 618.112 786.17163.0758.4454.69C68 819.994 655.543 918.39184.4961.5752.78

当砂土垫层厚度相同(组合梁跨度的1/20～1/10)时，落体冲击能量越大，砂土耗能越大但比率越小。C4砂土耗散能量较C1大678.35 J，C5较C2大988.83 J，C6较C3大1 277.28 J；C4砂土耗散能量百分比较C1大15.37%，C5较C2大14.94%，C6较C3大14.48%。因此冲击能越大，同等增加的砂土垫层厚度(组合梁跨度的1/20增加到1/10)所耗散的能量越大但耗能比率有降低。

3.3 跨中位移

通过对比表2和表7，SPH-FEM方法和试验得到的测点位移相差在1 mm以内，数值模拟和试验拟合较好。

表7 数值模型测点挠度Tab.7 Deflection of the measuring point of numerical models

4 回归分析

SPH-FEM模型选取混凝土圆台落体的冲击能和级配中砂垫层的厚度作为研究参数。将砂土垫层厚度设定为α，落体冲击能β，砂土耗散能量γ。α取值分别为0.05 m，0.1 m，0.15 m，0.2 m和0.25 m。落体高度取值分别为1 m，2 m，3 m，4 m和5 m。重力加速度取值为9.8 N/kg，β则分别为2.205 kJ，4.41 kJ，6.615 kJ，8.82 kJ和11.025 kJ。

4.1 砂土耗能

经过数值计算后得到各组的砂土耗能，如表8所示。通过回归分析得到砂土垫层厚度、落体冲击能与砂土耗能的关系。回归统计的基本数据，如表9所示。其中αβ，α2β,β,β2,β3的t统计量的P值远小于显著性水平0.05。因此这5项自变量与γ相关。其中砂土垫层厚度与落体冲击能共同作用时对砂土耗能的影响最大；落体冲击能比砂土垫层厚度对砂土耗能的作用更为重要。

砂土垫层厚度、落体冲击能与砂土耗能的关系，如图12所示。当砂土垫层厚度相同(组合梁跨度的1/40～1/8)，砂土耗能与落体冲击冲击能成正比。当落体冲击势能相同时，砂土垫层耗能与砂土垫层厚度(组合梁跨度的1/40～1/8)成正比。回归方程式(2)可通过不同厚度的砂土垫层和落体冲击能得出砂土耗能，为钢-混凝土组合梁防护工程的设计提供参考依据。

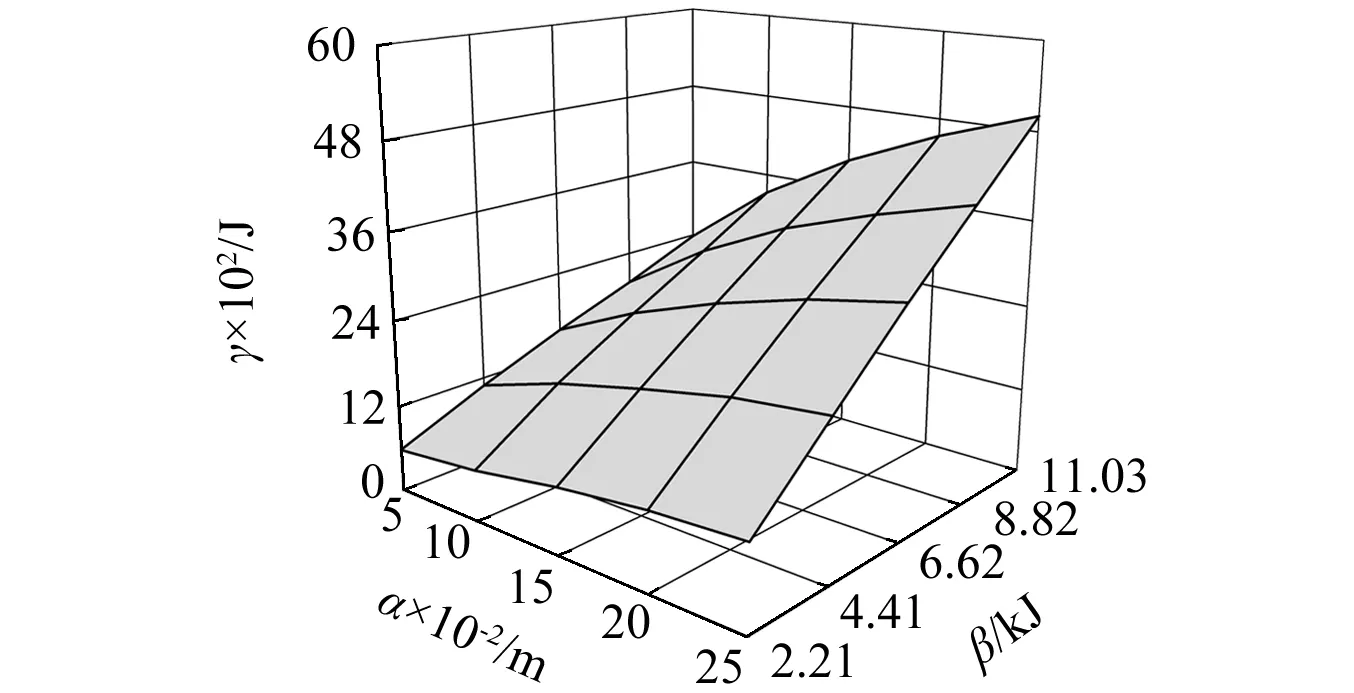
图12 砂土耗能与其余参数的关系Fig.12 Response surface of dissipation energy and other parameters

表8 砂土耗能与最大冲击力计算结果Tab.8 The summary of the dissipation energy of sand

表9 回归统计的基本数据Tab.9 Basic data of regression statistics

γ=-120.244+1 037.557α+272.247β-6 884.51α2-18.583β2+

2 661.73αβ+18 497.33α3+0.732β3-3 949.06α2β-2.925αβ2

(2)

4.2 最大冲击力

最大冲击力是防护工程设计的关键因素。目前冲击力的计算公式均基于弹性接触力学模型和试验[17-22]。然而方法只针对砂砾土垫层并忽略了结构的影响，且研究对象均为球体。圆台形状落体的研究较少。

砂土垫层厚度、落体冲击能与最大冲击力的关系,如图13所示。回归方程式(3)可通过不同厚度的砂土垫层和落体冲击能得出砂土覆盖下钢混凝土组合梁中圆台的最大冲击力，为钢-混凝土组合梁防护工程的设计提供参考依据。表10表明落体冲击能对于落体的最大冲击力的影响最大；其次为砂土垫层厚度、砂土垫层厚度与落体冲击能共同作用。

图13 最大冲击力与其余参数的关系Fig.13 Response surface of maximum impact force and other parameters

γ=146.267+6 712.169α+226.998β+39 291.885α2-34.341 8β2+

183.376αβ-67 600α3+1.715β3+200.557α2β-22.442αβ2

(3)

5 结 论

为了研究落石冲击作用下覆盖钢-混凝土组合梁上砂垫层的耗能性能，进行6根梁的模型试验和25根梁的SPH-FEM分析。选用落体冲击能和砂土垫层厚度两个参数，得到以下结论:

(1)砂土在防护工程中对钢-混凝土组合梁起到的耗能作用明显。组合梁跨度1/20～1/10的厚度的砂土垫层可以明显减小钢筋混凝土面板的最大裂缝宽度和组合梁的最大挠度。组合梁的最大挠度和裂缝宽度与冲击能量的大小和砂土垫层耗能强弱有关。

(2)砂土层厚度从0.1 m增加至0.2 m，冲击能越小(落体高度从4 m降低至2 m)，砂土起到缓冲冲击力的作用越明显。

(3)当砂土垫层厚度相同(组合梁跨度的1/20～1/10)时，落体冲击冲击能越大，砂土耗能越大但比率越小。冲击冲击能越大，同等增加的砂土垫层厚度(组合梁跨度的1/20增加到1/10)所耗散的能量越大但耗能比率有微小降低。当砂土垫层厚度相同(组合梁跨度的1/40～1/8)，砂土耗能与落体冲击冲击能成正相关。当落体冲击冲击能相同时，砂土垫层耗能与砂土层厚度(组合梁跨度的1/40～1/8)成正相关。

(4)落体冲击能、砂土垫层厚度相互作用时对砂土垫层的能量耗散效率的影响最大。落体冲击能对于落体的最大冲击力的影响最大。通过回归统计得到的公式可以通过不同厚度的砂土垫层和落体冲击能计算出砂土消耗的能量和落体的最大冲击力，为钢-混凝土组合梁防护工程的设计提供参考依据。