推进剂利用系统连续液位测量滤波算法研究

李 强 胡元威 董余红 马小龙

(北京宇航系统工程研究所，北京 100076)

1 引 言

与常规推进剂利用系统采用点式液位传感器不同，低温推进剂利用系统采用电容式连续液位传感器，实时采集箭上贮箱内的液位信号并以此为依据利用对阀门进行的控制，调节推进剂的混合比。液位信号测量的精确程度直接影响到利用系统的调节功能，决定了运载火箭推进剂的剩余质量[1]。如何提高液位测量的精度，确保液位测量信息的正确性成为低温推进剂利用系统研制中的关键问题[2]。

为了减小飞行过程中由液位晃动引起的测量误差，提高液位测量的精度，本文介绍了火箭飞行过程中低温推进剂的液位测量原理，对测量过程中出现的误差进行了分析，针对目前液位测量中的错节问题，提出了一种基于推进剂流量的滤波算法，并对算法进行了数学建模与仿真。仿真结果表明该算法可以有效解决火箭飞行过程中由于液位晃动造成的测量误差问题，具有一定的工程应用价值。

2 低温推进剂连续液位测量原理

低温推进剂液位测量一般选用电容分节式液位传感器，液位传感器的工作原理与一般的同轴圆筒式电容液位传感器的工作原理基本相同，液位高度变化时传感器利用被测液体与周围介质不同的介电常数，将液位转化成电容量变化来表征输入信号的大小以实现液位的测量。当传感器浸入被测介质中，随着介质液位的变化，液体包围探极的面积随之改变，使构成电容器两极的相对面积改变，导致电容量的变化[3]。

与一般电容液位传感器不同的是，推进剂利用系统把传感器外电级分为偶数个分节，并把分节电容分成两组，一组为偶数组，另一组为奇数组，两组电容分别接入变压器电桥，作为两个电容臂交替工作，电桥输出的信号经过放大、检波、整流、滤波后输出直流电压，在传感器的测量范围内输出完整的“三角波”。火箭飞行过程中推进剂贮箱内液位随时间下降，液位的高度曲线如图1(a)所示，经传感器测量，将液位高度信号转换为直流电压信号，如图1(b)所示，传感器输出信号为两个电容臂交替工作产生的“三角波”信号。利用系统工作时，液位计算单元接收“三角波”电压信号，通过电压信号判断贮箱液位的实际高度。

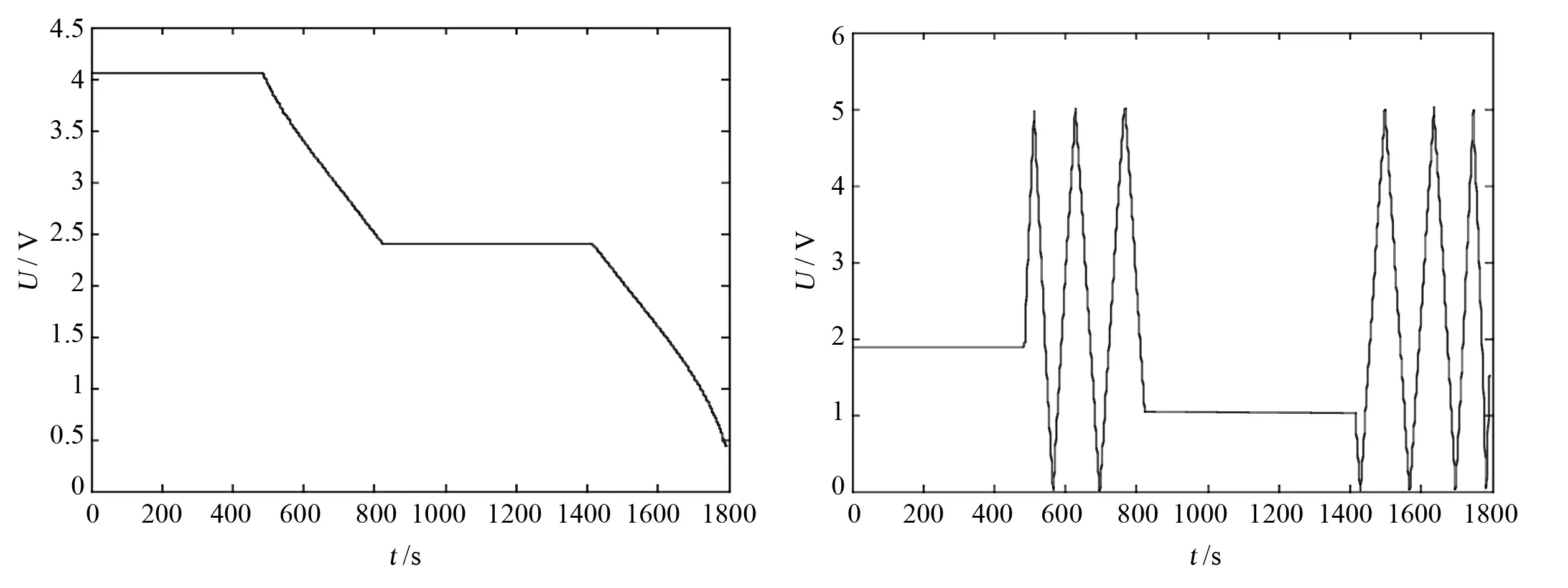
(a) 实际液位 (b) 测量电压信号

3 液位测量中的滤波问题

分节式液位传感器具有结构简单可靠、分辨率高，且误差不累计等优点[7]。虽然使用这类液位传感器在结构上具有独到之处，但由于低温推进剂液面的沸腾、火箭飞行中的液面晃动、以及叠加了一定的输出电压信号上以及低频交变分量。这种“三角波形”信号电压给箭-地计算机在数据采集处理和计算上带来一些关键技术难题[4]。

3.1 液面周期扰动的消除

作为液位高度的直接来源，如何消除或抑制电压值的周期性(晃动)和非周期性(沸腾)扰动，是直接影响系统测控精确性可靠性和系统稳定性的关键技术问题。这是因为分节电容式液位传感器、变换器的输出电平在理想条件下是一系列“三角波”电平，但火箭在实际环境下的飞行过程中由于受到各种扰动，在“三角波”电平上叠加了一个低频交变分量，需要采用数字滤波的数据处理方法，即运用滑动平均法对采样序列进行预处理，然后再对新的序列进行逐段的直线拟合，最后给出U的估值。

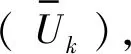
(1)

式中:m——采集的点数。逐段拟合的直线方程为

(2)

式中:S——逐段拟合点数；ΔT=mΔt,Δt=采样间隔时间。

该直线方程由最小二乘法得到并解析出a,b后可得

(3)

3.2 三角波的记数

利用分节电容式液位传感器测量推进剂液位高度时，除了需要“三角波”的电压值外，还需定位电压值所处的“三角波”节数[4]。这就需要对传感器输出电平信号的波峰与波谷处进行识别与记数，即节数记数。要求绝对可靠，否则丢掉一个节数就意味着液位测量误差为一节传感器的长度，这将远远超出给定的误差允许范围[5]。另一方面由于输出波形的“拐点”并不十分明显而是一个区间，因此就存在着一个实时的“拐点”识别问题。

传感器拐点识别逻辑示意图如图2所示。“三角波”信号在波峰和波谷处分别有最大输出电平Umax和最小输出电平Umin，设定波谷最大信号电平阀值为Umaxf，最小信号电平阀值为Uminf，电平的上升沿为正斜率(K>0)，下降沿为负斜率(K<0)。液位数字处理器在判断与识别传感器的输出信号是否到达拐点和过拐点时，其根据一是信号电平的大小是否位于阀值区，二是斜率极性是否改变。如果两个条件同时满足，则完成对传感器节数的更新。

为了提高判节算法的可靠性，避免漏判，三角波的最大信号电平阀值与最小信号电平阀值往往与真实的最大电平与最小电平间存在一定缓冲区域，因此当电平信号进入判节区域时，若存在晃动则可能产生多余的节数记数，造成较大的液位测量偏差。如何确保节数记数的正确性，有效滤除多余的记数信息则成为低温推进剂连续液位测量中急需解决的问题。

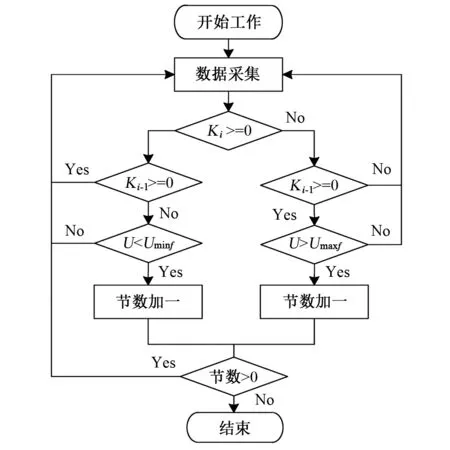
图2 传感器拐点识别逻辑示意图Fig.2 Logic diagram of sensor inflection point recognition

4 基于流量的液位滤波算法

4.1 基于流量的滤波门限设置

发动机流量由地面多次发动机试车后得到的数据包络给出，通常情况下，运载火箭飞行过程中的推进剂流量固定在标准流量的一定偏差范围以内。换句话说，发动机正常工作时，推进流量的变化范围已知。根据这个已知的偏差范围，可以将火箭飞行时由于晃动或其他原因造成的液位晃动有效地剔除。

推进剂流量保持在一定范围内，意味着推进剂液位高度下速度V相对恒定(贮箱柱段)。因此正常飞行时，推进剂液位经过每节传感器的时间也相对固定，可以通过一个时间包络Tb表示。

与正常的发动机流量变化造成的传感器节数变化频率相比，由于晃动液位变化造成的传感器节数变化频率较高，两者之间存在较大差别，可以通过此差别对连续液位测量中的传感器节数信息进行滤波。通过利用液位处理器记录推进剂液位“过节”时间td，与Tb进行比较，当td超出范围Tb时，去除过节信息。

4.2 算法流程设计

算法流程图如图3所示，算法步骤如下：

a)开始采集连续液位变换器输出电平；

b)对系统采集的电平值进行实时的平滑滤波；

c)根据平滑后的电平值计算“三角波”斜率、判断是否过节；

d)若未发生过节，则重复上述步骤；

e)若发生过节，记录过节时间，并与上次过节时间相减(首次过节不判断)；

f)判断过节时间差值(td)是否满足过节门限(Tb)，若满足节数加一，若不满足，节数不变，继续进行节数判断。

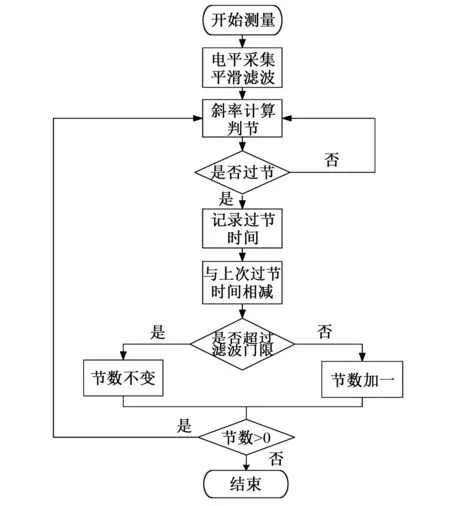
图3 程序流程图Fig.3 Program flow chart

5 数字仿真及结果分析

以某型号氧箱为例进行液位测量滤波算法的仿真验证，首先通过仿真得到加入晃动数据的液位高度，在此高度数据的基础上采用本文的滤波算法进行推进剂液位高度的测量，对滤波算法的有效性进行考核。

5.1 液位信号仿真

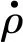
(4)

根据发动机额定流量计算飞行过程中芯级贮箱推进剂液位的高度。在不考虑晃动和偏差的情况下对液位高度进行仿真，结果如图4(a)所示。

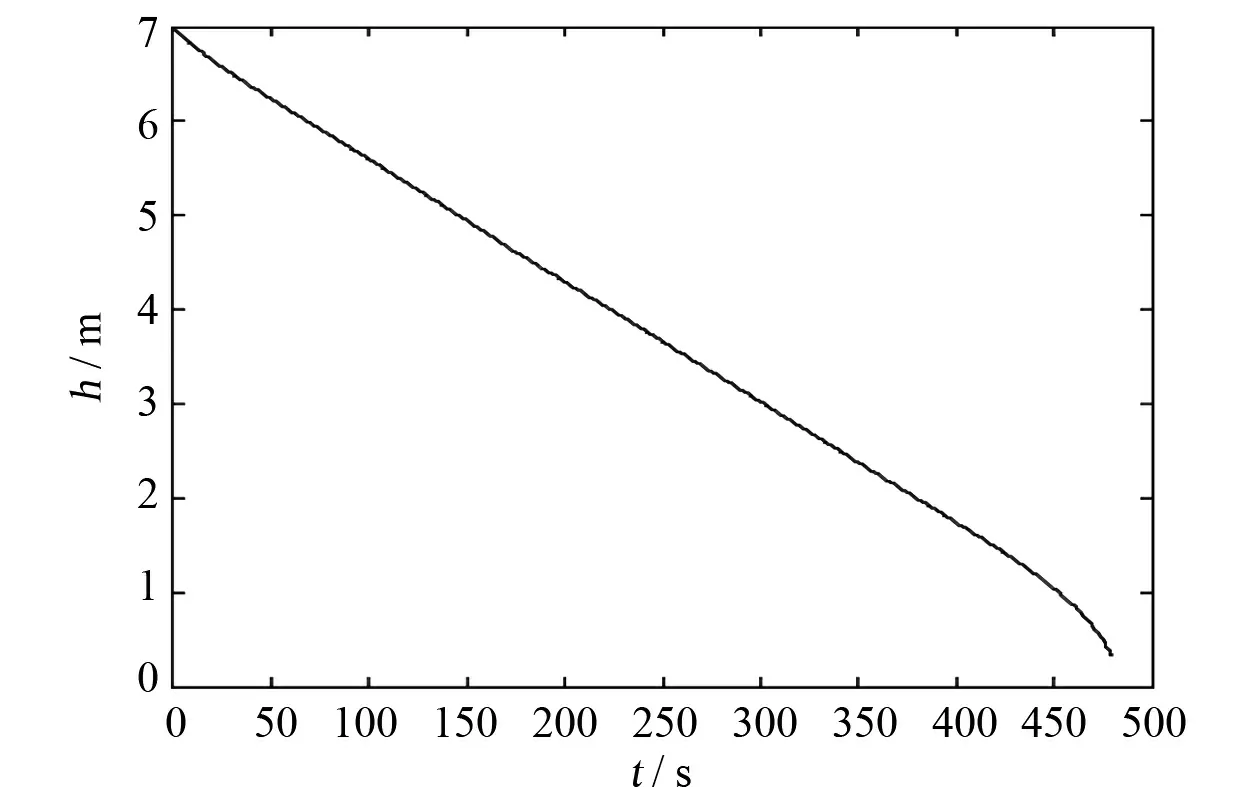
(a) 无晃动液位高度 (a) Non sloshing level height

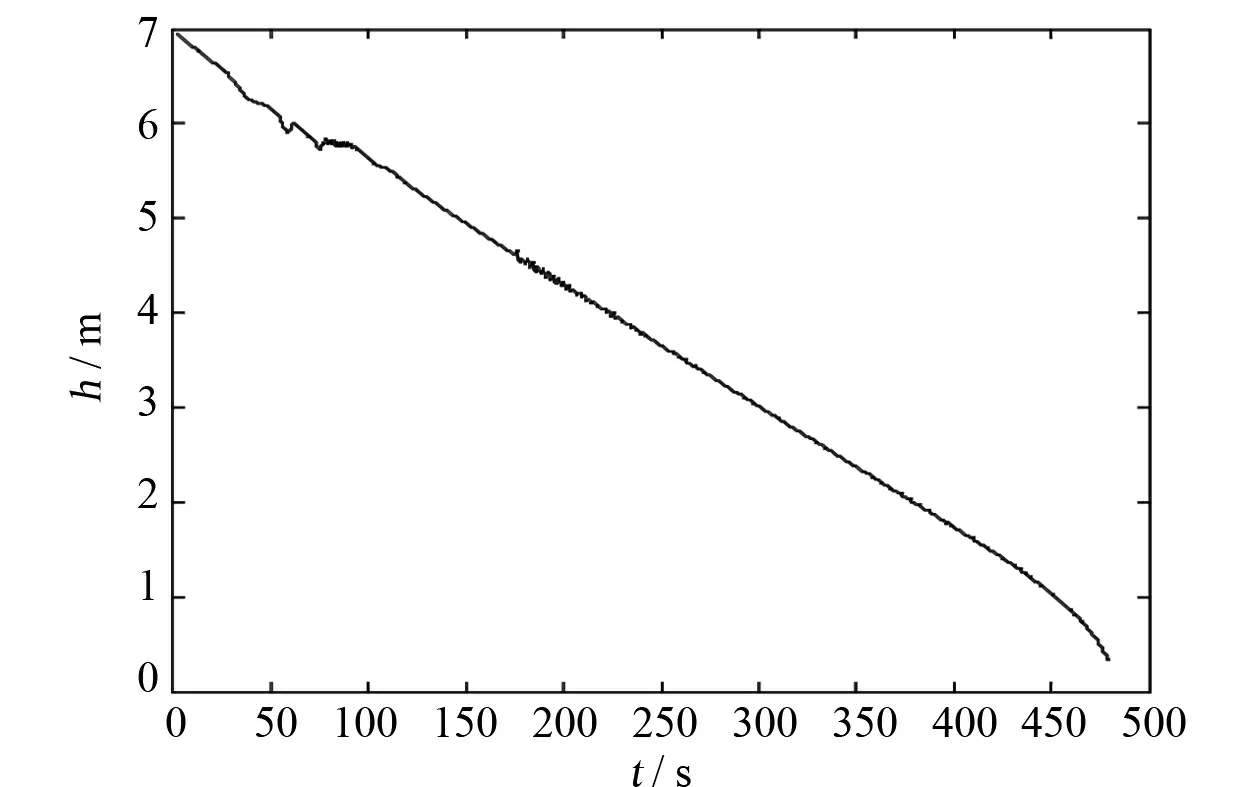
(b) 加入晃动后液位高度 (b) Height of liquid level after adding sloshing图4 液位高度仿真曲线Fig.4 Simulation curve of liquid level height

真实飞行中，运载火箭经历大风区飞行、助推分离、一二级分离以及姿态调整等过程，对箭体的稳定性产生一定影响。在各种扰动下，由于箭体姿态运动导致各级贮箱内的推进剂产生晃动，对液位高度的测量带来一定影响。根据姿态动力学方程小偏差模型进行姿控系统仿真，获取飞行过程中弹簧振子的晃动位移，推进剂的晃动液高与晃动质量位移成一定关系，如下式所示

(5)

式中：η——推进剂液高;y——弹簧振子的晃动位移;ξ1——晃动系数;he——推进剂液位高度;R——贮箱半径。根据晃动特性数据，将推进剂晃动位移转化为推进剂晃动液高随时间变化的曲线，模拟真实飞行情况下的推进剂在贮箱内的运动情况，将晃动加入液位高度曲线，可以得到晃动情况下的液位高度变化曲线，如图4(b)所示。

5.2 三角波电压仿真

推进剂液位信号经过液位传感器、变换器后由三角波信号表示。得到晃动液位高度数据后，需要将其转换为三角波电压信号作为滤波算法的输出。三角波电压信号模型如下

(6)

式中:U(t)——实时输出的液位传感器电压;v1、v2——分别代表三角波的最大最小电压;T——下降周期;n——周期数。

根据贮箱内传感器的安装情况，对飞行过程中各贮箱采集到的三角波电压信号进行仿真，可以得到模拟飞行过程中的液位测量电压信号，数据曲线如图5所示。

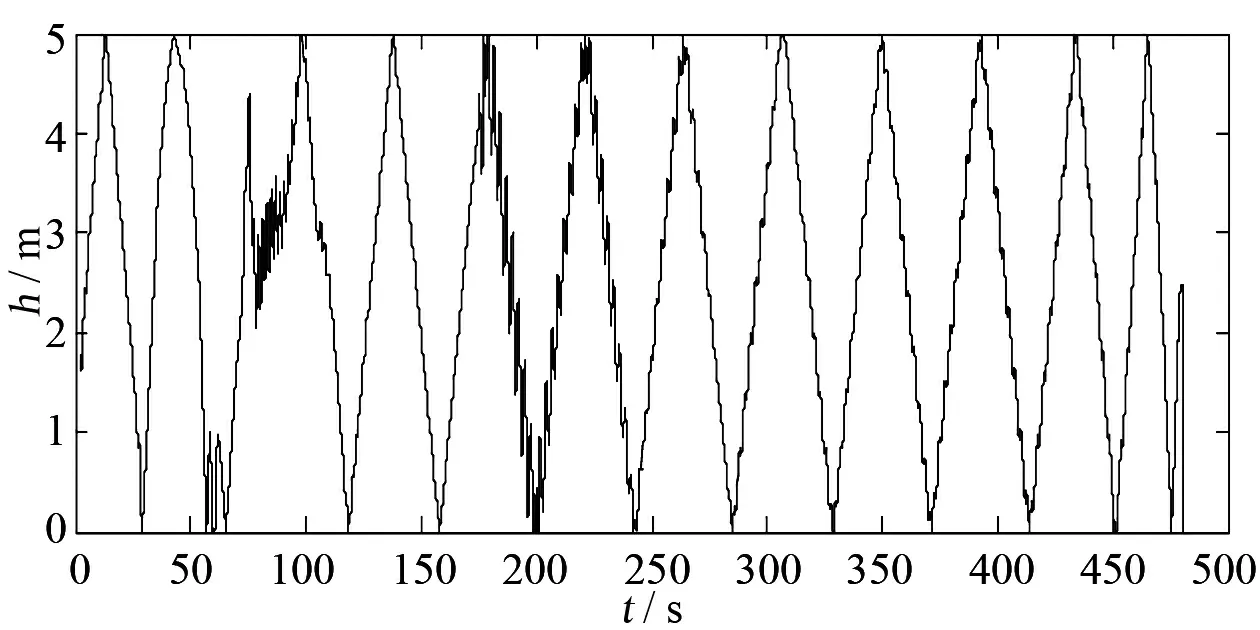
图5 加入晃动的三角波电压信号Fig.5 Added sloshing triangle wave voltage signal

5.3 对滤波算法的考核

将仿真得到的三角波电压信号作为输入数据，采用本文提出的滤波算法，对加入晃动的三角波电压仿真数据进行液位测量，测量高度曲线如图6所示。图6中同时也给出了使用现有测量算法测得的液位高度曲线，通过比较可以得出，现有算法在液位晃动的情况下出现了传感器节数计算错误，造成了较大的液位高度偏差。表1、表2中给出了两种算法下的传感器节数记数值，比较后可以发现，现有测量算法无法滤除由于液位晃动带来的虚假“过节”信息。而采用基于流量的液位滤波算法测量得到的高度曲线与图4(b)中的仿真高度数据一致，证明了滤波算法的有效性。

图6 液位高度测量曲线比较Fig.6 Comparison of liquid height measurement curves

表1 现有判节算法的传感器节数记数Tab.1 Sensor node count for existing algorithm

表2 加入滤波算法后的传感器节数记数Tab.2 Number of sensor nodes after adding filtering algorithm

6 结束语

通过介绍低温推进剂连续液位的测量原理，对现有算法在测量过程中出现的误差进行了分析；针对液位测量中的错节问题，提出了一种基于推进剂流量的滤波算法，并根据推进剂消耗、推进剂晃动等数学模型进行了推进剂液位高度的数字仿真；在仿真数据的基础上对本文提出的滤波算法进行了考核。仿真结果表明，该算法有效地滤除了飞行过程由于液位晃动产生的液位测量误差问题，是实现利用系统液位测量的一种理想的算法，具有一定的工程实用价值。