基于Spark的并行遗传算法在温稠密物质状态方程构建中的应用

李媛媛，张庆伟

(1.北京信息科技大学 理学院，北京 100192；2.北京奇虎360科技有限公司，北京 100015)

0 引言

状态方程[1]是描述物质系统中各状态变量之间关系的函数表达式，用来表达在一定热力学条件下物质的性质。通常人们研究最多的是力学响应特性的状态方程，即所谓的狭义状态方程。温稠密物质[2-3]是一种不常见物质，广泛存在于地幔内部和宇宙星体内，具有高的能量密度特性。温稠密物质中存在复杂的电离效应，精确了解不同粒子的电离程度，可以更好地了解强耦合下温稠密物质内各种粒子和束团的状态与成分。

在科学研究中，想要获得温稠密物质的状态方程十分困难。只有在超高压超高温的情况下，才会出现温稠密物质，一般需要通过核聚变实验进行相关研究，但是花费巨大，所以目前许多研究学者已经使用遗传算法来获得状态方程。王成[4]提出基于基因遗传算法和γ律状态方程的JWL状态方程参数的确定；温丽晶[5]采用遗传算法确定PBXC03等炸药轰爆产物JWL状态方程的参数，应用确定的状态方程参数模拟爆轰驱动远观过程，计算结果与实验结果符合。这2篇文献的算法都没有采用并行，效率较低，精确度较差。张庆伟[6]提出的基于Spark的并行遗传算法得到了较为理想的效果。本文使用基于Spark并行遗传算法来确定温稠密物质状态方程的参数。

1 温稠密物质实验数据

本次实验的数据选自王聪等建立的氢(氘、氚)的密度泛函第一性原理宽区状态方程数据库[7]。数据主要为氢、氘、氚在极端条件下的压强、密度、温度和内能。其中的密度范围为10-3～103g/cm3，温度范围为103～107K。按照密度划分为31组，每组有13～21条数据。本文的研究都是基于表1的数据。

表1 氢在极端条件下的数据

2 状态方程

2.1 状态方程形式

在自然界中很多物质的状态方程是未知的，所以本文需要先根据实验数据确定状态方程的形式。在密度固定时，压力和温度之间存在着一定的函数关系，假设两者之间的函数关系为

f(T,P)=0

(1)

表1中每组数据为1321条不等，而泰勒的三阶展开需要10个参数，四阶展开需要15个参数，为了可以求解到一组唯一解，选择三阶展开，式(1)在(0,0)处的三阶泰勒展开式为

f(T,P)=A+BT+CP+DT2+ETP+FP2+

GT3+HT2P+ITP2+JP3+ο3

(2)

式中：A,B,C,D,E,F,G,H,I,J为状态方程对应的参数；T、P分别为温度、压强。

考虑到随着密度的增大，压力增大的速度极快，可以达到107，为了方便计算，对T和P分别取对数，令t=log10T,p=log10P，代入式(2)，得

f(t,p)=A+Bt+Cp+Dt2+Etp+Fp2+

Gt3+Ht2p+Itp2+Jp3+ο3

(3)

从31组不同密度的数据中，每组选10个数据代入式(3)，每10组数据都会得出一个式(4)，再对式(4)求解非线性方程组即可以求出一组唯一的参数(A,B,C,D,E,F,G,H,I,J)。

f(t,p)=

(4)

2.2 参数确定

采用矩阵法可以求出对应31组密度的温稠密物质状态方程参数。表2为部分结果。

表2显示不同的密度对应的温稠密物质状态方程的参数，考虑是否可以寻求到ρ和每个参数之间的函数关系。令：

(5)

式中(ma0,ma1,ma2,ma3,ma4)为参数A在不同密度下所对应的的参数。同理，对于所有的参数，都有一组(m0,m1,m2,m3,m4) 与之对应。其矩阵式为

(6)

式中[An,Bn,Cn,Dn,En,Fn,Gn,Hn,In,Jn] (n∈[1,31])对应着表2中节选的部分数据。可求出每个参数对应的一组m值，如表3所示。表3为使用ρ的对数进行计算得出温稠密物质状态方程参数在不同密度下所对应的参数。把表2中得到的状态方程的参数代入式(7)中即可求出温稠密物质状态方程：

A+Bt+Cp+Dt2+Etp+Fp2+Gt3+

Ht2p+Itp2+Jp3+ο3=0

(7)

表2 矩阵法求得状态方程参数的部分结果

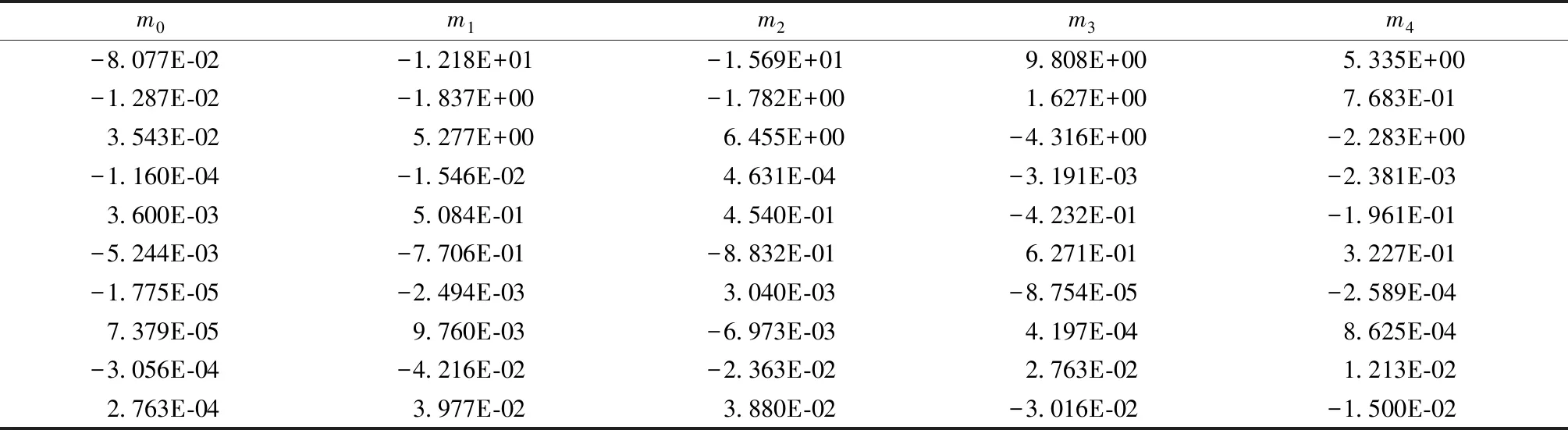
表3 参数结果矩阵法求解的状态方程参数在不同密度下对应的参数

2.3 矩阵法的不足

矩阵法可以求出相应的状态方程，但是存在一定的缺陷。因为不同密度对应的数据量不同，上面的算法只选用了其中的10组数据，虽然可以求出一组确定解，但是该解对未参与计算的数据的适用性有一定的不确定性。虽然可以通过后期验证其适用性，但是解一旦确定后就无法修改。如果求得的解不适应未参与计算的数据，则会导致该解无效。所以针对上述方法的缺陷，本文使用基于Spark的并行遗传算法来确定状态方程的参数。

3 数学模型及状态方程的确立

3.1 数学模型

张庆伟提出基于Spark的并行遗传算法可以解决理想气体的状态方程的参数，并且计算结果良好,在计算时间和结果的精度上都取得了较好的效果。本文将该方法用于确定温稠密物质状态方程参数，使用Scala[8-9]语言编写基于Spark的并行遗传算法程序，将其在一台服务器的虚拟机上运行。Leque[10]介绍了3种遗传算法的并行方式：分布式模型、蜂窝煤模型和混合模型。Spark是一种主从式的分布式计算框架，适用于全局分布式的并行遗传算法。但传统的遗传算法不能直接结合spark来确定状态方程的参数，需要对传统遗传算法进行改进。主要针对以下几个方面。

1)传统遗传算法始终在一个固定的空间内进行迭代，算法效率低下，基于spark并行遗传算法将固定的空间设计为变化的搜索空间。具体方法为：将最初的搜索空间划分为若干个子区间，且每个子区间对应不同的子种群，将子种群及其对应子空间放到不同的节点上进行运算，选择得到最小适应度个体所在的子空间，再将其继续划分，达到不断变化搜索空间的效果。

2)因为基于spark并行遗传算法需要不断地变化搜索空间，所以变化的子空间的子种群也需要同步更新，然后再对状态方程未知参数的取值范围进行划分，在每个子空间上随机生成子种群，再将生成好的种群写入文件中，每行代表一个区间的所有个体及其所在的取值空间，以便后续使用，此时子种群已生成。

3)在产生子种群后生成新种群，然后对新种群个体进行适应度评价，通过适应度函数方法得到新种群的最小适应度、对应区间、最小适应度对应的个体，再把所有的数据回收到主节点，在主节点上选择最小适应度值所在的取值空间，将空间重新划分，产生子种群，将产生的子种群继续划分若干子种群，直至满足截止条件，将适应度最小的个体保存下来，并将其加入新的子种群中，这样就重新选定了搜索空间。

4)传统遗传算法有的只并行适应度函数的计算，有的只并行遗传操作。为了将遗传算法和spark相结合来确定状态方程中的参数，将传统的串行遗传算法[11-12]进行了改进：①算法中包含2个函数并行运行，一个是遗传操作的并行，另一个是获得个体适应度函数的并行运算。因为产生新种群替代旧种群需要的循环次数多，且选择、交叉、变异等操作也比较费时，所以遗传比获得个体适应度需要更多的时间成本；②针对遗传算法中的迭代操作。首先初始化迭代次数，判断是否满足截止条件，满足返回新种群，否则进入迭代，从Pstring[13-14]中获得状态方程的参数区间，获得种群，判断新种群个体数是否等于旧种群个体数，如果达到就将旧种群中适应度最小的个体替代新种群中适应度最大的个体，进行下一次迭代；否则就选出2个个体，进行遗传操作，将新产生的个体加入到新种群中，直到新种群中的个体数满足条件。在基于Spark的并行遗传算法中，因为状态方程形式未知，所以遗传算法中适应度函数的确定难度变大，根据表1中数据，由于温度和压强存在一定的函数关系，令

(8)

则适应度函数可以写为

(9)

式中n为每组数据的数量。

3.2 状态方程参数的确定

表1中的t、p值是通过物理实验测得，将t值和用遗传算法产生的p值代入式(9)，根据适应度函数的变化情况确定状态方程的参数。表5为所求状态方程参数的部分结果。

表5 遗传算法所得状态方程参数的部分结果

与矩阵法相同，遗传算法对于所求得的参数和密度之间也存在一定的函数关系，令

(10)

式中γ1、γ2、γ3、γ4、γ5分别为参数A、B、C、D、E在不同密度下所对应的参数。

适应度函数为

(11)

式中z为数据分组数。使用遗传算法求出参数在不同密度下所对应的参数，如表6所示。

表6 遗传算法求解的状态方程参数在不同密度下对应的参数

4 实验结果分析

本文中的矩阵法和基于Spark的并行遗传算法使用的都是表1中的数据。2种方法在不同密度下误差的变化趋势如图1所示。

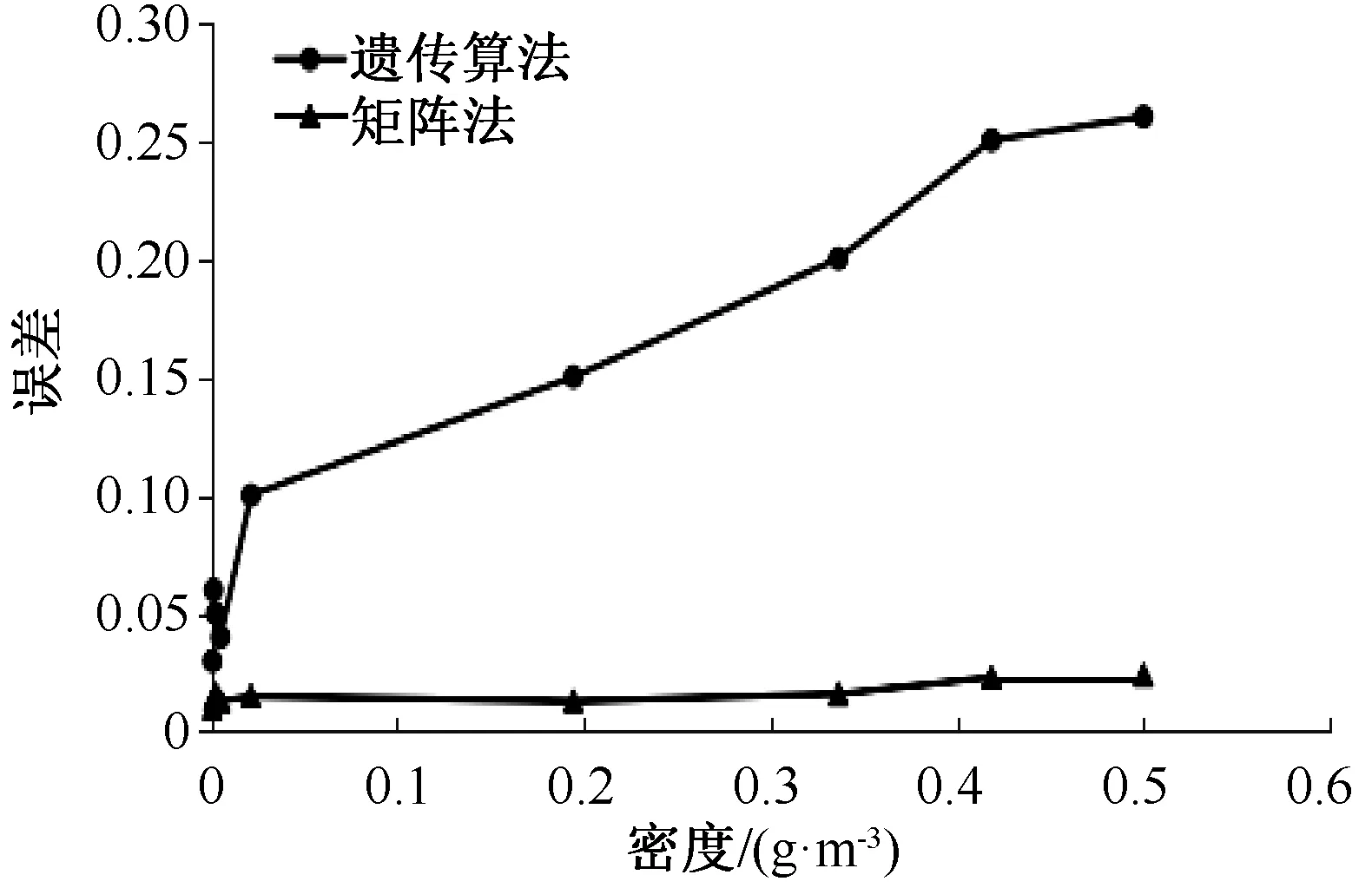
图1 不同分组的实验结果误差

从图1可以看出，使用矩阵法所得的参数较为精确，使用遗传算法所得结果的精度较矩阵法有所下降，且随着密度的增大，遗传算法求出的数据与物理实验测得数据的误差也越来越大。主要原因是随着密度的增加，压强变化范围也逐渐增加，且增长速度很快，过大的范围容易产生状态方程的分区域问题，即不同的温度和压强区域状态方程的参数和结构都会发生变化，导致误差逐渐增大。

图2是2种方法在相同密度下所求参数的平均误差。从图2可以看出，矩阵法对应的10个参数的平均误差不够稳定，尤其是A、B、C误差过大，根本无法满足要求。而遗传算法对应参数的平均误差极小且十分稳定。

图2 不同参数对应的误差

结合图1和图2可以看出，对于不同密度分组下的参数求解，矩阵法求得温稠密物质状态方程参数的误差在密度偏大的时候要优于遗传算法的结果；但是，对于在相同密度时，求温稠密物质状态方程参数平均误差时，遗传算法在精度和稳定性上都要优于矩阵法。此外，矩阵法所求的参数对数据的依赖性更大，只适用某些数据，该解对未参与计算的数据适用性有一定的不确定性；而遗传算法的解基本可以忽略与物理实验的数据误差，更加精确。

5 结束语

为了尽可能减少实验次数，利用更少的数据获得更加准确的状态方程，本文采用基于Spark的并行遗传算法构建温稠密物质状态方程。实验结果表明，本文方法所求温稠密物质状态方程参数的稳定性优于矩阵法。对于密度逐渐增大时，遗传算法会有较大误差的问题，可以考虑把不同温度、密度和压强进行分区域研究，以便得到更精确的结果。