多传感器时滞系统CI融合滤波算法

李璇烨，高国伟

(北京信息科技大学 传感器重点实验室，北京 100101)

0 引言

多传感器的数据融合问题，就是如何组合局部观测，或是如何使局部状态估值器精准地得到一个融合的状态估值器，最终使融合得到的精度要比每一个局部状态估值器得到的精度都高。在多传感器信息传输时，会存在时滞现象，时滞现象是引起系统性能差以及不稳定的主要原因。因此，在对多传感器信息进行融合时，消除系统中的状态滞后与观测滞后成为当前研究的热点[1-4]。文献[5]对于离散系统提出了线性最小方差估计(Kalman滤波)，由2个同系统同等维数的立卡提方程求得最优估值器，它远远小于系统增广方法的计算负担。孙书利等[6]提出了在状态噪声与观测噪声不相关时按标量加权融合算法，该算法计算负担小，有利于随时应用。但该算法没考虑到局部估计误差相关性[7-9]。

考虑到目前分布式估计研究现状，本文在分布式融合框架下，对带有多传感器时滞系统融合估计问题展开研究。针对带有网络诱导时延无线传感器网络和不确定模型，本文提出了一种基于分布式协方差交叉(covariance intersection，CI)融合滤波估计方法。

1 问题阐述

考虑带有L个传感器的离散多重时滞随机系统

(1)

i=1,2,…,L

(2)

式中：x(t)∈Rn为系统的状态；y(i)(t)∈Rmi为第i个传感器的观测；白噪声v(i)(t)∈Rmi及ω(t)∈Rr(i=1,2,…,L)分别为第i个传感器的观测噪声与系统噪声；φk(t)、γ(t)和hk(i)(t)为维数适当的时变矩阵；d≥0为最大状态滞后，di≥0为第i个传感器的最大观测滞后(i=1,2,…,L)[10]。

假设1ω(t)∈Rr和v(i)(t)∈Rmi(i=1,2,…,L)是零均值的相关白噪声，即

(3)

式中：Qv(ij)(t)=Qv(i)(t)；E为期望；δtk为Kronecker delta函数。

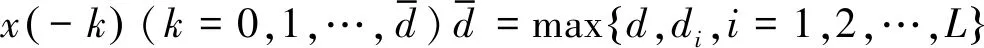
(4)

X(t+1)=Φ(t)X(t)+Γ(t)ω(t)

(5)

(6)

其中

(7)

对多传感器时滞系统的融合滤波，就是在假设1与假设2下，求CI融合Kalman滤波算法。

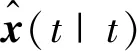
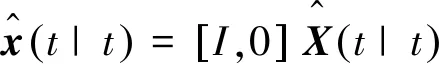
(8)

对于系统(2)，当di=0时，观测时滞消失，只剩下状态时滞，因此可以得到带有L个传感器的离散状态时滞随机系统：

(9)

y(i)(t)=H(i)(t)X(t)+v(i)(t)

i=1,2,…,L

(10)

对于系统(1)，当d=0时，状态时滞消失只剩下观测时滞，因此可以得到带有L个传感器的离散观测时滞随机系统：

x(t+1)=Φ(t)x(t)+Γ(t)ω(t)

(11)

i=1,2,…,L

(12)

2 局部最优稳态Kalman滤波器

引理1在假设1与假设2情况下，增广系统具有最优Kalman滤波器[11]：

K(i)(t+1)ε(i)(t+1)

(13)

(14)

ε(i)(t+1)=Y(i)(t+1)-

H(i)(t+1)X(i)(t+1|t)

(15)

K(i)(t+1)=P(i)(t+1|t)H(i)T×

(16)

H(i)T(t+1)+QV(t+1)

(17)

(18)

P(i)(t+1|t+1)=[In-K(i)(t+1)×

H(i)(t+1)]1(i)(t+1|t)

(19)

引理2对于系统(5)与系统(6)的局部稳态Kalman一步预报器为[11]

(20)

Ψpi=Φ[In-KHi],Kpi=ΦKi

(21)

(22)

式中Σi满足稳态Riccati方程：

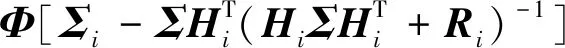
ΦT+ΓQΓT

(23)

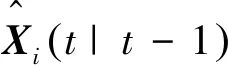
3 CI融合Kalman滤波器

在两传感器系统中，当2个传感器各自的协方差P1、P2均已知，互协方差P12未知时，应用CI方法[13-15]，可以得到CI融合稳态Kalman滤波器为

(24)

(25)

式中ω为权系数，且0≤ω≤1。

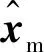
(26)

(27)

将式(24)与式(25)相比，若将P1-1和P2-2分别放大ω和1-ω倍，即分别令

(28)

则由式(25)定义的PCI-1可由不相关估值式(26)的形式来表示，即

(29)

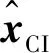
(30)

将式(28)代入式(29)与式(30)中，最后可以得到CI融合算法为

(31)

(32)

极小化性能指标为

(33)

对非线性最优化问题，可用黄金分割法[12]进行快速搜索而得到最优权系数ω0。

本文分别采取ω=0.1，0.2，…，0.9进行搜索，取得最优权系数ω0=0.391 36。

4 精度分析

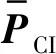
(34)

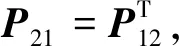
(35)

定理2局部融合Kalman滤波器之间精度关系[15]

(36)

5 仿真结果与分析

基于传感器网络场景中的移动目标的追踪问题，建立了3个传感器节点分别对移动中的目标运动状态进行采样，其系统方程可近似的表示为

(37)

i=1,2,3

(38)

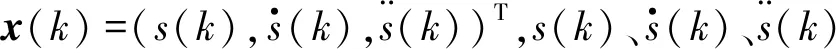
将该系统转化为无滞后系统为

X(t+1)=Φ(t)X(t)+Γ(t)ω(t)

(39)

Y(i)(t)=H(i)(t)X(t)+V(i)(t)

i=1,2,3

(40)

其中

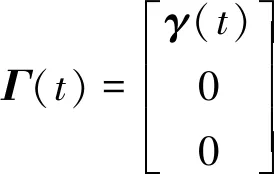
状态系统中各参数分别为

观测系统由三传感器组成，分别进行移动目标位置、速度与加速度的监测，模型中各观测矩阵与噪声方差参数分别选取为

使用该模型进行100次仿真。为了表明所提出

的分布式CI融合滤波算法的有效性，与分布式加权融合方法进行了比较，结果如图1与图2所示。

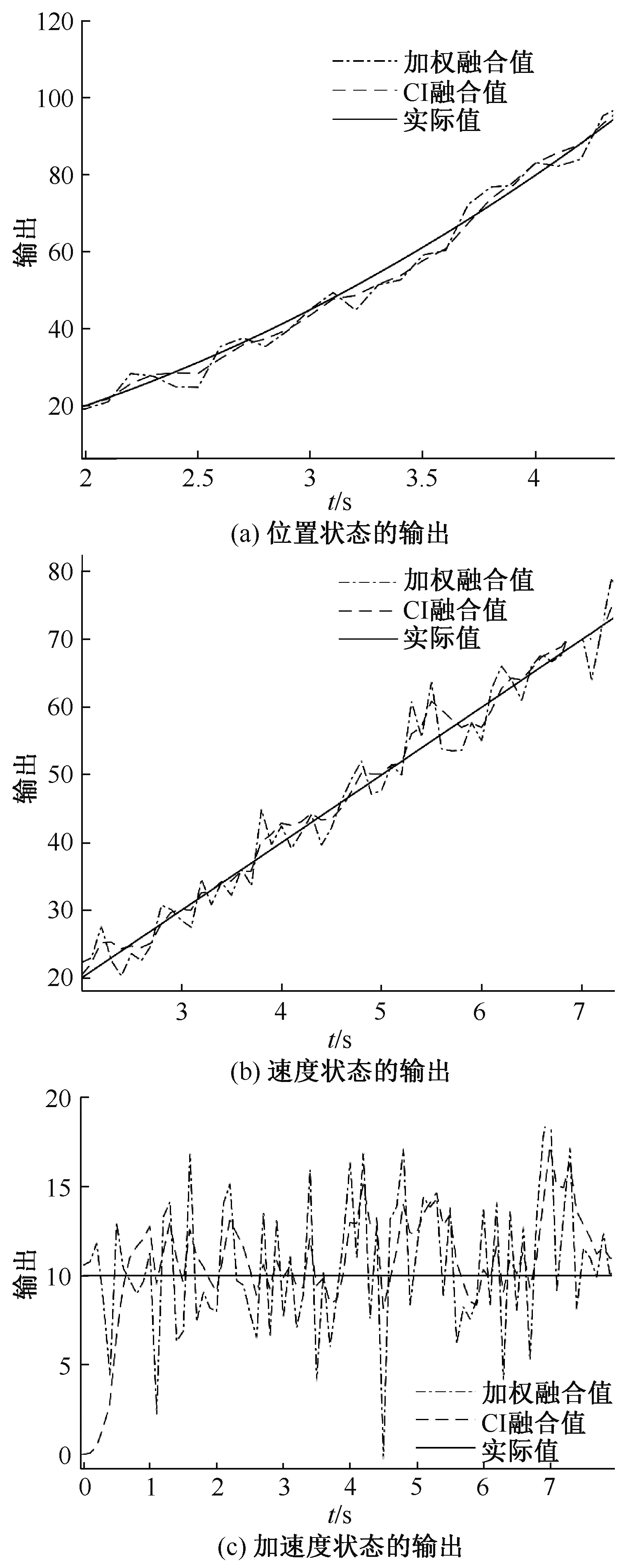
图1 两种方法对位置、速度、加速度状态的估计

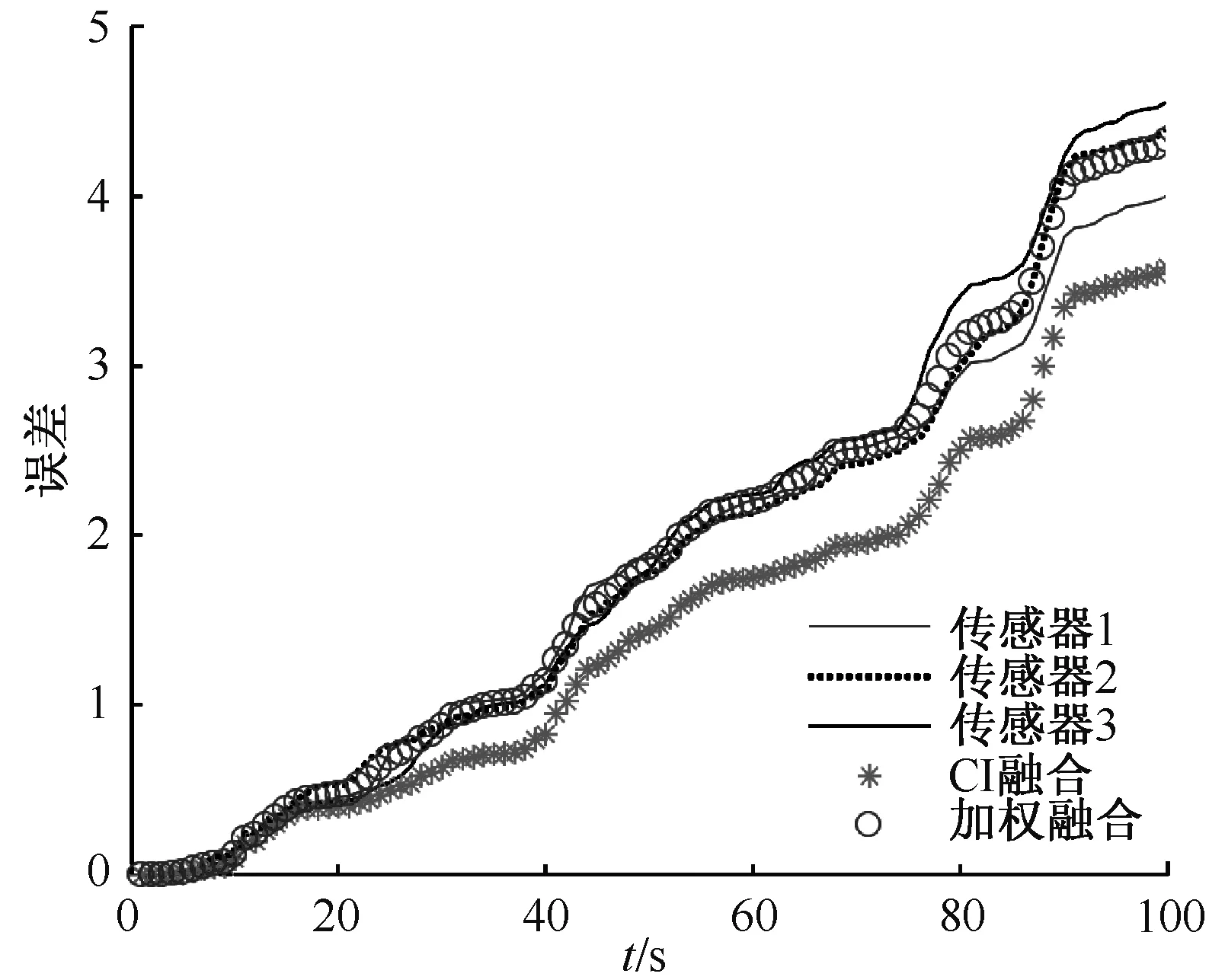
图2 三传感器局部融合Kalman滤波器与CI融合估值器MSE曲线比较

由图1可知，在系统存在时间滞后的情况下，本文提出的分布式CI融合估计算法具有很好的跟踪效果；另一方面，局部估计和融合估计的误差协方差如图2所示，CI融合的MSE曲线是处于每一个局部MSE曲线以及加权融合后的MSE曲线的最下方，可知CI融合器实际的精度高于每一个局部滤波器的精度，且接近最优融合器的精度；而且对任意互协方差，相对应的CI融合器可能的最差精度依旧高于每一个局部滤波器的精度。

6 结束语

本文针对带观测滞后与状态滞后的三传感器系统，设计了一种具有一致性的CI融合稳态Kalman滤波器。该算法利用增广矩阵将时滞系统化为非时滞系统，并且由于CI算法可不必计算局部估计的互协方差，因此大大减轻了计算量，也节约了计算时间。并证明了该滤波器的精度比每一个局部Kalman滤波器的精度都要高。仿真结果表明，它的精度非常接近于最优融合Kalman滤波器的精度，所以其性能较好，有一定的实用价值。