基于门槛模型的双向FDI溢出效应研究

类 骁

(北京信息科技大学 信息管理学院，北京 100192)

0 引言

开放经济条件下资本的跨地区流动与配置以及知识的非排他性为地区的技术进步和创新提供了潜在发展动力，学界称此类知识的非自愿流出现象为“技术溢出”[1]。大量国内外研究证实了“技术溢出”正向效应的存在，但也有少数研究持不同看法[2-4]。随着全球化进程的不断加快，双向FDI(外商直接投资FDI, foreign direct investment;对外直接投资OFDI, outward foreign direct investment)已成为东道国获取跨国资本“技术溢出”的重要渠道，特别是对于发展中国家而言，利用并发挥双向FDI的溢出正效应是实现“技术追赶”的关键[5]。

国际上最早研究双向FDI溢出效应的是Lichtenberg(1998)，他首次将国际研发溢出划归为贸易进出口、FDI和OFDI三个渠道，并给出了溢出权重测算公式，为研究跨国资本溢出提供了基础理论框架，后文简称LP模型[6]。国内对双向FDI溢出效应的研究起步较晚，研究思路大致可归纳为两条：一是溢出作用对象的扩展，林进智[7]实证发现FDI溢出促进了我国的制度创新，贾妮莎等[8]研究发现FDI和OFDI溢出对我国产业结构升级均有促进作用，且后者作用更明显；二是样本的分组实证，由于我国发展不平衡性问题依旧突出，很多研究关注于区域差异性问题，何兴强等[9]等发现FDI溢出存在明显的地区差异性，东部地区因人力资本水平高能有效的吸收FDI溢出，尹东东等[10]研究了研发投入、人力资本、经济发展水平等因素对OFDI逆向技术溢出的影响，实证发现东中西部溢出表现和促进因素差异明显。

总体来看，现有文献对双向FDI溢出的研究对象十分发散，绝大多数研究均采用线性的静态面板模型进行回归分析，未考虑变量之间作用的非线性关系，因此估计结果存在较大偏误。基于此，本文遵循已有的研究脉络，构建双向FDI溢出面板门槛模型，分析双向FDI溢出的门槛限制因素及其对我国区域技术进步的非线性门槛作用。

1 门槛模型构建与变量说明

1.1 方法与模型构建

Hansen[11-12]提出了面板数据的门槛自回归模型，重点研究非线性门槛问题，不需要给定非线性方程的形式，门槛值数目由样本数据内生决定，同时基于渐进分布理论建立待估参数置信区间。门槛自回归模型思想是将门槛值作为未知变量引入模型，构建变量系数的分段函数，对门槛值及门槛效应进行估计检验。设x1,i为自变量，对样本进行划分的门槛变量设为qi，门槛模型方程为

yi=θ0+θ1,qi≤γx1,iI(qi≤γ)+

θ1,qi>γx1,iI(qi>γ)+Xjiθj+εi

(1)

第一步，在门槛变量的取值范围任选q1代入方程，对实证模型进行系数估计，计算出残差平方和S1(q1)；第二步，任选另一q2代入方程，求得新系数及残差平方和S1(q2)；第三步，比较2个残差平方和，取较小的S1对应的门槛变量值，作为门槛值qmin的初始值；第四步，再任选一q3，方法同第一步，得到新系数及残差平方和S1(q3)，与qmin所对应的残差平方和比较，取较小的S1作为新的门槛值γ；第五步，重复上述步骤，直到找到qn，其所对应的残差平方和为最小为止，此时qn为门槛值γ的最终取值。同时，Hansen还提出了利用Bootstrap法模拟渐进分布，并给出了变量系数检验的具体方法和门槛真实性的检验思路。

基于Hansen门槛回归思想，本文将模型被解释变量选取为区域技术水平；除核心解释变量FDI和OFDI溢出量外，根据Griliches-Jaffe知识生产函数并结合文献对技术驱动因素及滞后性分析，选取区域研发能力、人力资本、经济发展水平为控制变量；近年来高技术产业规模成为我国跨国投资业务的重点领域，是经济增长和科技创新的核心竞争优势所在，但较低的研发强度可能会对跨国资本的溢出效应产生影响，因此选取高技术产业研发强度为门槛变量。

综上，以FDI溢出为例构建面板门槛模型如下：

β4lnRi,t-1+β5lnGi,t+ξi,t+ui,t

(2)

式中：i为地区；t为年份；TTFP为区域技术水平；Sfdi、Sfdi为FDI、OFDI溢出量；H为区域人力资本；R为区域研发能力；G为区域经济发展水平；δ为高技术产业研发强度；γ为门槛值；α0为截距项；β为弹性系数；ξ为截面固定效应；u为随机扰动项。

1.2 指标测度

近年对G20国家综合效应的研究成为热点，但多关注于G20国家的经济效应，鲜有对其技术效应的研究，因此本文选取除中国外的G20国家为技术溢出方(因个体差异带来的偏误，样本不包括欧盟)，截取2008-2017年我国30个省份(因数据可得性原因，不包括西藏、港澳台地区)面板数据进行研究。

(3)

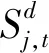
(4)

式中：OOFDIi,t为i地区当年对外直接投资额；OOFDIt为我国对外直接投资总额；OOFDIj,t为我国对j的对外直接投资额。

区域技术水平本文采用DEA-Malmquist方法的全要素生产率进行测度，投入产出要素分别为各地区产出、劳动力和资本存量[13]。人力资本采用受教育年限方法测算[14]；研发能力采用基于永续盘存法的研发资本存量衡量，取折旧率15%；经济发展水平考虑到技术水平与人口密度存在一定关联，选取人均GDP指标测度；为反映区域间高新技术研发的投资差异，高技术产业研发强度采用各地区高技术产业R&D经费支出占总研发投入比重测算。

本文使用的数据来自对应年份的《中国统计年鉴》、《中国科技统计年鉴》、《中国对外直接投资统计公报》和世界银行统计数据库WDI。

2 模型实证

2.1 平稳性检验

对变量数据进行单位根检验，结果显示变量值或差分值在通常显著性水平上(1%或5%)通过了检验，证明面板数据序列平稳或一阶差分平稳；对变量协整关系进行Pedroni检验，结果如表1所示，Panel ADF及其他检验均在显著性水平1%下拒绝“不存在协整关系”的原假设，说明变量间存在协整关系。

表1 Pedroni检验结果

注：括号内为P值。

2.2 模型回归

为检验双向FDI溢出是否存在国别异质性，将样本国家分为发达国家和发展中国家两组分别估计。使用Stata12.0编写Hansen门槛检验和回归程序，对模型进行估计，结果见表2和表3，其中检验“自抽样”次数设为500。

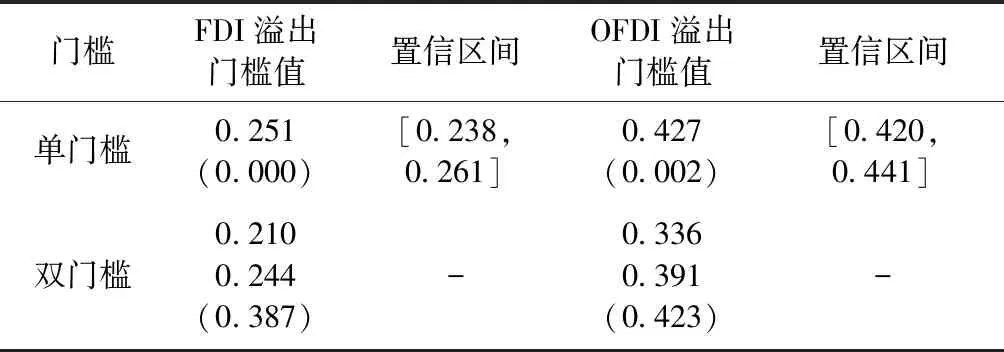
表2 门槛效应检验结果

注：括号内为P值。

表3 面板门槛模型估计结果

注：括号内为t值。

3 结果分析及建议

第一，研发能力、人力资本是区域技术水平提升的重要驱动力。前者系数在0.48～0.56之间，后者系数在0.27左右，再次证实了两者对技术发展的正向推动作用[15]。未来须继续深度挖掘内部动力，引导全社会加大对研发的投入力度，优化研发资源有效配置，重视高技术人才培养及人才体系的建设。

第二，FDI溢出和OFDI溢出存在显著的以高技术产业研发强度为门槛的单门槛效应，门槛值分别为0.251和0.427，且至少通过了5%的显著性检验。FDI溢出和OFDI溢出与区域技术进步呈“U”型关系，即只有当地区的高技术产业研发强度跨过门槛“拐点”时，溢出才表现为正效应，系数分别为0.177和0.045。为此要积极开展与技术领先国家在高技术产业更大范围、更宽领域、更高层次的合作；统筹和优化国内高技术产业布局，合理引导人才、科研机构转向中西部地区，激发当地跨国资本的溢出正效应。

第三，整体来看，FDI溢出与区域技术进步表现为显著的正向关系，系数为0.124，说明外商投资以“示范效应”和“培训效应”为主[16]；OFDI溢出表现为微弱的负向关系，系数为-0.028，原因是目前我国高质量和技术获取型海外投资比重过低，投资多以利用当地优惠的税收政策和补贴为主，OFDI反向溢出无法有效为技术提升赋能。

双向FDI溢出的国别异质性明显，发达国家FDI溢出促进作用十分显著，系数为0.197，远高于发展中国家和平均水平，但OFDI溢出作用不明显且不稳健；发展中国家FDI溢出和OFDI溢出均呈显著的负效应，无法推动本地的技术提升。

基于此，要进一步改善产业投资环境，引导外资投向，深化与发达国家的合作往来，鼓励并扶持技术获取型投资项目，优化海外投资产业构成，加大对信息技术、交通运输、能源等高新技术产业的可持续性投资。

4 结束语

本文选取G20国家为技术溢出方，既具备热点性，又补充了对G20国家技术效应研究的相对不足；在模型和方法上一是提出了中观层面FDI和OFDI的溢出权重计算公式，二是通过构建门槛模型纠正了传统面板数据模型在估计上的偏差，刻画了溢出对技术进步的非线性作用机理，并从国别异质性等多个角度开展分析。研究发现双向FDI溢出均显著的存在基于高技术研发强度的单门槛效应，证实了溢出对区域技术进步的分区间、非线性影响，只有当跨过“高技术产业研发强度”门槛拐点时，FDI溢出和OFDI溢出才表现为正效应。本研究为我国今后的外商投资与对外投资发展提供了参考和建议，为区域技术提升的驱动因素研究提供了模型基础，今后可将BP神经网络算法与Hansen门槛面板模型相结合，进一步提升拟合方法的完备性。