基于BL-SMOTE和随机森林的不平衡数据分类

张宸宁，李国成

(北京信息科技大学 理学院，北京市 100192)

0 引言

数据不平衡问题已经成为训练分类模型乃至数据挖掘的关键问题。类别不平衡数据会导致分类模型的准确率衰弱，从而导致实际效果受到影响。近年来，学者们提出了许多处理这类问题的方法。剖析这些方法可以将它们大致分为两类：一类是从数据层面处理不平衡数据；另一类是从算法层面处理不平衡数据。

在数据层面，主要是对数据进行重采样，重建其训练集使样本数据分布更加真实，主要包含欠采样技术和过采样技术。过采样技术的基本思想是增加少数类样本，使其原始分类信息能够得到较好的保留。过采样的算法主要有SMOTE算法[1]、LN-SMOTE算法[2]、SMOTE-RSB算法[3]等。欠采样技术主要是删除部分多数类样本，但会造成分类信息不完整，数据丢失严重。在欠采样技术中，有区分使用K-NN分类器识别多数类中相关实例的方法[4]，还有遗传算法中的一个分支演化的进化算法[5]以及Tomek链接的相互邻近关系方法[6]等。在对某些类样本分类准确率要求较高的领域，通常选择过采样技术。在算法层面，主要是修改在数据集上算法的偏置，使决策平面偏向于少数类，提高对少数类的识别率，并对现有问题通过重新设计算法来解决不平衡数据问题。通常情况下，使用过采样技术来实现机器学习分类器的多样化。其中使用过采样技术的算法主要有SMOTEBoost算法[7]、SMOTEBagging 算法[8]以及RAMOBoost 算法[9]等。在提前执行每一个欠采样来调整集成方法中有Under-Bagging算法[10]、粗糙平衡Bagging算法[11]以及RUSBoost算法[12]。除了基于集成方法外，还有其他内部平衡方法，例如主动学习策略[13]以及粒度计算等。这些方法在一定程度提高了SMOTE的性能。但SMOTE算法没有对少数类样本进行有区别的选择，即使Borderline-SMOTE算法通过设置边界点集来实现对少数类样本的区别选择，这种设置也存在着一定的不合理。

本文针对类别不平衡本身的性质，在SMOTE算法基础上，融合检验数据准确性的常用统计方法——本福特法则，提出一种新的数据处理方法，即BL-SMOTE算法。利用本福特法则对少数类样本进行有区别的选择，使用本福特法则对近邻样本进行合成，使其数据分布更真实。同时，用随机森林进行分类，并采用3种最为常见的评价指标，对我国上市公司财务数据集进行实证研究。最后，与证监会公布的造假公司信息进行对比，结果表明BL-SMOTE算法的分类效果优于SMOTE算法，同时验证了在数据分类方面，相比于逻辑回归、决策树、梯度提升树，随机森林的效果更优。

1 相关知识

1.1 SMOTE算法

SMOTE(synthetic minority over-sampling technique)算法[1,14]在2002年提出并得到认可，它的基本思想是通过人工合成新的少数类样本来降低类别不平衡性。其中基本原理是在近邻少数类样本之间进行线性差值，合成新的少数类样本。具体做法是：假设邻近参数为k，首先从每个少数类样本的x个同类最近邻中随机选择k个样本；然后将每个少数类样本分别与选中的k个样本按式(1)合成k少数类新样本；最后，将新样本添加至训练样本集中，形成新的训练样本集。

xnew=x+δ(y[i]-x)

(1)

式中：xnew为合成的新样本；x为少数类样本；δ为0到1之间的随机数；y[i]为x的第i个近邻样本。

值得注意的是，在SMOTE算法中邻近参数k是否能够合理设置将直接影响最终的分类性能。通常设置邻近参数k=5。

1.2 本福特法则

在实际数据中，普遍认为所有数字应该随机出现并且具有相同的概率。然而实验表明并非所有数字出现的概率都是相等的，而是像{1,2,3}这样的低位数比{7,8,9}这样的高位数更频繁地出现。这种数字现象被称为本福特法则。在十进制中，本福特法则即为首位数字出现的概率，即

(2)

式中pd为通过数据样本点首位第d个数字的概率。

本福特定律广泛运用于地质学、化学、天文学、物理学和工程学有关数据，以及会计、财务、计量经济学和人口统计学的集中数据。尤其在检测欺诈行为中，可以检查财务报告中的数据是否符合本福特法则，从而能够规避逃税、金融诈骗等风险。这是由于欺诈者通常不了解这种数字模式，并倾向于人为修改具有近似相等频率的数字。同样，由于SMOTE算法是人工合成新样本数据的算法，在选取新样本数据的权重时，采用0～1之间的随机数作为选取新样本数据的权重，却未考虑到人工生成的数据是否违背自然界规律。因此，本文借助于本福特法则能够检测欺诈行为以及符合自然规律的特点，运用本福特法则的卡方值替换SMOTE算法中生成新样本数据的权值，设计了一种新的算法——BL-SMOTE算法。相比SMOTE算法，该算法借助本福特法则本身特性，更精准地模拟出符合自然规律的新样本数据。

1.3 随机森林

随机森林[15](random-forest)是由多个决策树组成的集成分类器，它是用来解决预测问题的学习模型。采用{h(x,θk),k=1,2,…,m}表示m个决策树，其中θk为独立同分布的随机向量。针对自变量，从m个决策树中选出一个最优分类结果：

(3)

式中：H(x)为随机森林模型；I(*)为示性函数；hi为单个分类模型；Y为输出变量。

从式(3)中可以看出类别对评估变数的重要性。另外，在创建随机森林时，它可以在内部对于一般化后的误差产生不偏差的估计；对于不平衡分类，可以平衡误差。以上特点使得随机森林对处理样本量级小的数据集具有优势。

2 BL-SMOTE算法

针对SMOTE算法的不足，本文结合本福特法则提出了一种改进型SMOTE算法，即BL-SMOTE算法。BL-SMOTE算法主要思想是给少数异常类样本(即负样本)有选择地建立权值，样本权值服从本福特法则的概率卡方值(即本福特选择方法)，并人工合成近邻的负样本。

不同于SMOTE算法，在生成样本数据时，选取的权重为随机数。考虑到本福特法则的有效性在各个领域已得到证明和验证，本文为改善权重的准确性，利用本福特法则的卡方值替代SMOTE算法中随机数产生虚拟负样本数据。

2.1 本福特选择方法

效仿遗传算法选择算子，按照一定的规则从当前种群中选择出一些符合要求的个体遗传到下一代种群中，其原则是权值高的个体以较高的概率成为下一代个体。BL-SMOTE算法中的本福特选择方法继承了这一思想，它是从少数类样本中以较高的概率选择出权值较高的样本，使得新合成的样本聚集在该样本附近。

本福特选择方法步骤如下：

(4)

(5)

式中：pcd为数据样本点首位第d个数字的实际概率，pnewd为数据新生成的样本点首位第d个数字的实际概率。

步骤2按照式(4)和式(5)计算少数类样本的选择概率：

(6)

步骤3按照本福特选择方法，将δnew作为BL-SMOTE算法中的权值。

2.2 BL-SMOTE算法流程

通过本福特选择方法计算出样本权值，再通过以下步骤，形成BL-SMOTE算法。BL-SMOTE算法具体流程如下：

输入： 训练集

st={(xi,yi),i=1,2,…,n,yi∈{+,-}}；正样本为样本数量级多的n+，负样本为样本量级少的n-，n++n-=n；不平衡比率rm=n+/n-；采样率为rs；近邻参数为k.

输出：过采样后的训练集

算法步骤：

1. 提取所有正负样本到训练集st中，组成st+与st-集合；

fori=1∶n-×rs

xnew=x-δnew(xnew-x)

图1进一步说明了BL-SMOTE算法的基本原理。图中五边形代表少数类负样本，圆圈代表多数类正样本。选中少数类样本，其近邻集合由最近的5个五边形组成，按照本福特选择方法作为新算法的权值，小五边形表示合成更准确的新样本。

图1 新样本的生成图示

3 实验结果与分析

3.1 不平衡数据的评价指标

通常采用分类准确性(xacc)来评估衡量分类模型的性能。分类准确性的数值越大数据准确率越高，算法效果越好。表1为分类结果的混淆矩阵。

表1 分类结果的混淆矩阵

在表1中,tp、tn分别表示原本就是正类、负类，并判断正确的样本数量；fp、fn分别表示样本真实类为负、正样本，却标记错误的样本个数。分类精度为

(7)

为了全面地对数据处理的效果进行评价，通常采用查准率：

(8)

查全率：

(9)

真负率：

(10)

为了平衡查准率、查全率的关系，采用信息检索(IR)领域常用的一种评价指标fmeasure进行性能评价测度，它常用于评价分类模型的好坏，其计算公式如下：

(11)

另外，为平衡真正率xTPR以及真负率xTNR的关系，采用Gmean进行性能评价测度：

(12)

Gmean是仅有在正负样本的分类精度同时都高的情况下，其值才会最大。本文使用fmeasure来衡量负样本的分类性能，使用Gmean来衡量数据集整体的分类性能。

3.2 实验结果与分析

为了验证算法的有效性，本文数据集采用wind中2007年至2017年所有上市公司的各季度的财务报表。其中财务报表也称为三张表，即利润表、现金流量表以及资产负债表。由于财务三张报表指标相对较多，且有些指标相互之间关联，本文选取影响财务数据最重要的46种指标作为特征，其中选取利润表10个特征，现金流量表20个特征，资产负债表15个特征以及日期。同时为了使正负样本不平衡程度有所差别，本文对数据集进行不同数量的随机划分，用以确定训练集和测试集。

以下所有实验结果均为循环200次所取得的平均值。本文采用Python 3.7实现了SMOTE算法、BL-SMOTE算法以及逻辑回归(LR)、ID3算法、分类回归树(CART)、随机森林(RF)、梯度提升树(GBDT)。将SMOTE算法和BL-SMOTE算法的邻近参数设置为同一树数值，保证它们合成的样本数目相同，然后使用以上5种机器学习方法进行分类。

图2至图4分别为某家上市公司在未处理不平衡数据集、使用SMOTE算法处理不平衡数据集以及使用BL-SMOTE算法处理数据集的混淆矩阵的示意图。

图2 某家上市公司未处理不平衡数据集的混淆矩阵

图3 某家上市公司使用SMOTE算法处理不平衡数据集的混淆矩阵

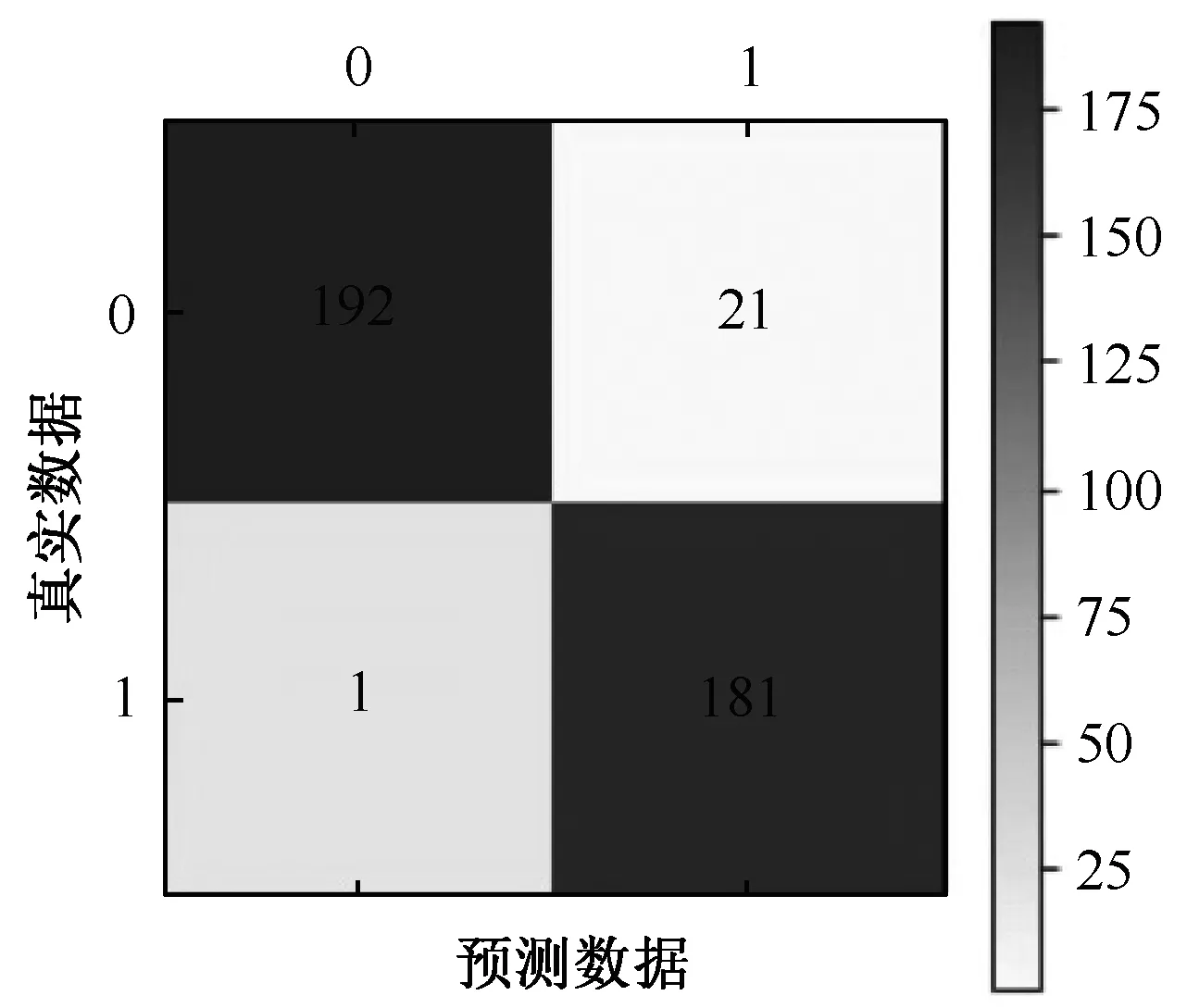
图4 某家上市公司使用BL-SMOTE算法处理不平衡数据集的混淆矩阵

将图2～4数据代入式(6)计算出某家上市公司未处理数据时xacc为0.192 0，在使用SMOTE算法处理数据时xacc=0.931 6，在使用BL-SMOTE算法处理数据时xacc=0.944 3。可见，对于同一批数据，采用BL-SMOTE算法处理时，分类准确性最高，即数据处理的效果最优。然而在工程应用中，样本真实类为负，错误标记成正类的样本相比于样本真实类为正，标记成负类的样本代价会更高，但是这一点无法从分类准确性xacc取值作出判断。

因此，通过3种评价指标的计算结果，综合判断5种机器学习算法在3种不同的处理数据情况下(即在未进行生成新数据的处理的情况、以及使用SMOTE算法和BL-SMOTE算法进行生成新数据的处理的情况)数值，数值越接近于1，效果越好。通过计算3种指标验证BL-SMOTE算法在处理不平衡数据的方面效果最优，并且验证相比其他4种机器学习算法，随机森林而分类方法最好。表2～4为3种不同情况下，5种机器学习的xacc、fmeasure、Gmean值：

表2 五种机器学习算法在不同情况下的xacc值

表3 五种机器学习算法在不同情况下的fmeasure值

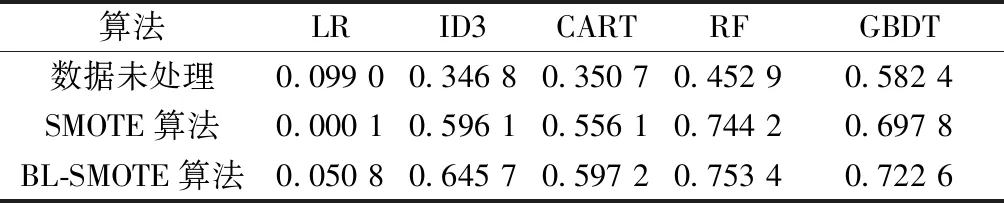
表4 五种机器学习算法在不同情况下的Gmean值

从表2～4可以看出，在3种不同情况下，随机森林算法较其他4种机器学习算法更接近于1，即效果最佳。因此选取随机森林算法作为数据分类器效果更好。

实验结果表明在随机森林机器学习分类器基础上，使用BL-SMOTE算法处理的不平衡数据xacc=0.944 3、fmeasure=0.944 3、Gmean=0.754 2，各项评价指标均高于其他情况。使用BL-SMOTE算法处理不平衡数据集准确率最高，从而验证了本文所提算法的有效性。

4 结束语

本文提出了一种新型的过采样技术，利用本福特法则在自然处理中的优势作为SMOTE算法的权值使数据更具真实性。在对所提出的解决方案进行更彻底的分析背景下，对所选数据集进行的初步实验的结果很重要。不同于以往使用UCI的数据进行模拟实验，本文运用更贴近于现代生活的真实数据，即上市公司近几年财务数据作为数据集，选取真实数据作为数据集的同时，数据的噪声也随之增大，清洗过程难度加大。通过比较BL-SMOTE和SMOTE以及机器学习算法本身的结果验证了BL-SMOTE算法的优势。不仅如此我们还考虑机器学习算法本身特性，在验证BL-SMOTE有效性和准确性，同时验证了多种机器学习算法的组合即决策树的集成算法，随机森林比单个机器学习算法(决策树)的效果更好。对于未来的工作，我们计划运用单个神经网络或者集群神经网络算法继续评估所提出的类别不平衡数据对来自各个领域的海量数据集的影响。另外，我们还希望将所提出的方法扩展到数字特征，使用高斯分布建模等。