基于状态反馈和扭矩前馈钻柱黏滑振动控制系统

付蒙, 李江红, 吴亚锋, 宋叔飚, 赵艾奇, 李文青

1．西北工业大学动力与能源学院，陕西西安710072;2．中国船舶工业系统工程研究院，北京100094; 3．太原学院市政与环境工程系，山西太原044300

在钻井过程中，由于钻柱深入地下几千米而且横截面积小、井底钻具组合转动惯量小、钻头和岩石间存在非线性摩擦力，容易引发钻柱黏滑振动现象[1-2]。钻柱黏滑振动主要表现为：恒定能量从顶驱输入至钻进系统，顶驱转速小幅度波动，钻头转速“黏滞-滑动-黏滞”交替出现。剧烈的钻柱黏滑振动发生时，钻头转速峰值可以达到正常转速的3～9倍[3]。钻柱黏滑振动容易导致钻柱连接器的松动，井底钻具组合各部件连接的松动，加快了钻进机械失效速度。严重的钻柱黏滑振动发生时，钻柱积累的扭矩超过其能承受的极限扭矩，会导致钻柱的断裂。为保证钻井安全和钻进的效率，许多研究致力于抑制钻柱的黏滑振动。

钻井深入地下几千米，难以直接获取井下钻进系统的状态，这就制约着全维状态控制器的实现。文献[4]通过反馈环节来控制钻柱黏滑振动的研究，但是设计方案需要测量井下相关的扭矩和速度，信号的测量、传输以及处理过程都不方便，而且井下环境恶劣，容易损坏传感器。文献[5]提出一种主动阻尼控制方式，并在此基础上研发了软扭矩控制系统。文献[6]基于钻柱分布式空间模型，提出一种比例积分控制器。但是此2种方案只有一个状态反馈量，致使其控制效果受到限制。文献[7]提出一种多维状态反馈控制器，文献[8]提出H∞控制器，文献[9]提出滑模控制器来抑制钻柱的黏滑振动，但是这些方案仍然需要获取所有的状态反馈量。为了获取井下状态量，文献[10]设计一种卡尔曼估计器，并通过LQR控制器抑制黏滑振动。但这些控制器仅仅局限于仿真验证，并没有应用于钻井现场。文献[2,10]分别设计观测器，估计钻柱扭矩或钻头转速。但是这些观测器设计都忽视非线性摩擦力，致使状态的估计不精确。目前，国内仍然缺乏对钻柱黏滑振动主动控制方法的研究。

文献[1]指出，钻柱黏滑振动是由钻头和岩石间的摩擦力引发的非线性自激振动。对钻头和岩石间的非线性摩擦力的精确描述仍然是一个世界性难题。在发表的诸多钻柱黏滑振动控制文献中，该非线性摩擦扭矩主要由Stribeck摩擦模型或者Karnopp摩擦模型来模拟，并且设定最大静摩擦扭矩和滑动摩擦扭矩为恒定值。但是在实际钻井过程中，岩层的变化会引起非线性摩擦力的变化。如果钻进系统的非线性摩擦力改变，驱动扭矩不足以克服非线性摩擦力，提出的一些控制方案可能失效。

针对上述不足，将反馈控制和前馈控制结合的全维状态控制器应用于抑制钻柱黏滑振动现象。该控制方案的创新在于：①仅仅测量顶驱转速和顶驱扭矩，即可完成全维状态控制器的设计；②设计了一种状态观测器，不仅可以估计所有的井下状态量，还可以估计非线性摩擦力；③针对变化的非线性摩擦力，提出一种参考值优化算法，一方面可以对状态参考值进行二次优化，另一方面计算最佳前馈控制量-驱动扭矩；④将设计的控制器应用于钻井现场并有效地抑制了钻柱黏滑振动。

文章建立了井下钻进系统的双自由度模型，系统阐述了控制方案、状态观测器和参考值优化算法的设计方法，在MATLAB中完成了对闭环控制系统的仿真验证，并最终应用于实际钻进。

1 钻进系统动力学模型

文献[8]通过模态分析，指出钻进系统双自由度集中参数模型的幅频特性和相频特性与有限元模型相近。文章以钻进系统双自由度集中参数模型为对象，研究了抑制钻柱黏滑振动的控制方案，如图1所示。

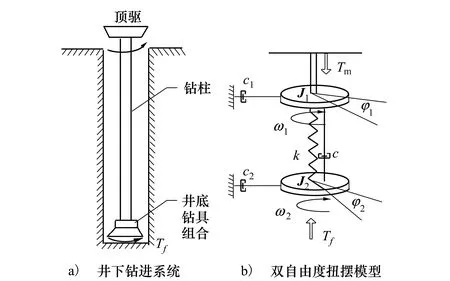
图1 井下钻进系统双自由度模型

基于双自由度集中参数模型及文献[3]对钻进系统的假设，用弹簧-转动惯量简化钻进系统。系统的运动方程：

(1)

式中,J1为顶驱转动惯量,J2为井底钻具组合转动惯量,c1为顶驱阻尼系数,c2为井底钻具组合阻尼系数,c为钻柱阻尼系数,k为钻柱刚度系数,φ1为顶驱角位移,φ2为井底钻具组合角位移(钻头角位移),Tm为顶驱扭矩作为系统的输入,Tf为非线性摩擦扭矩作为系统的扰动,ω2为井底钻具组合转速(钻头转速)。

为准确描述钻头转速在黏滞区间的连续性,利用Karnopp摩擦模型模拟钻具受到的摩擦扭矩Tf。非线性摩擦扭矩的表达式:

Tf(ω2)=

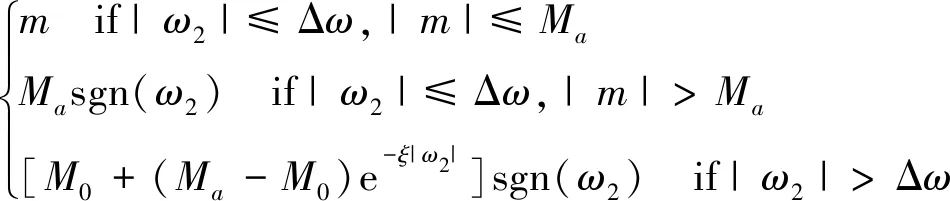
(2)

式中,m为钻柱耦合扭矩,Ma为最大静摩擦扭矩,M0为滑动摩擦扭矩,Δω为零速区间阈值,ξ∈[0,1]为经验常数并且定义了摩擦扭矩的下降率[3]。

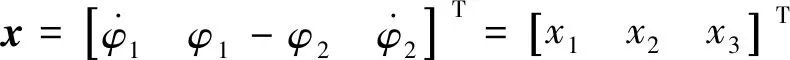
y=Cx

(3)

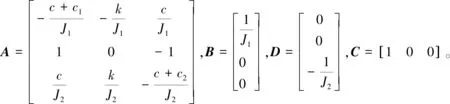
u=Tm为系统输入,A为状态矩阵,B为系统输入矩阵(向量),C为系统输出矩阵(向量),D为扰动输入矩阵(向量),y=Cx为可测量的输出变量。对于实际钻进系统而言,只有顶驱转速x1可以测量,其他状态均不可直接获取。

2 控制方案设计

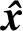
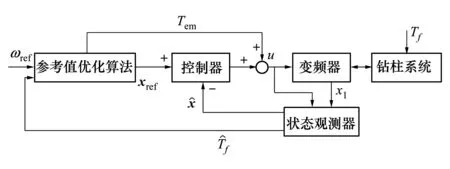
图2 控制方案结构图

2.1 状态观测器

系统(3)中,状态变量x2和x3以及非线性扰动变量Tf不可直接获取,只有系统输入u和状态变量x1(输出变量)可测。现有钻进系统观测器设计只以估计钻头转速为目的,不涉及摩擦力估计。这必然反向制约观测器的估计效果。基于Luenberger干扰观测器的设计方法,以阶跃扰动输入作为非线性摩擦扭矩的线性估计,选择合适的增益,获取状态观测器的动力学方程:

(4)

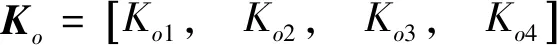
状态观测器(4)的特征多项式可以表示为

(5)

式中,T为时间常数,Di(i=2,3,4)为参数特征比。最优阻尼原理指出,当特征比Di=0.5时,系统阶跃响应超调大约为6%,调整时间大约为1.8T[11]。最优阻尼原理是一种基于闭环特征多项式的解析设计方法,一方面可以保证系统有比较好的动态特性,另一方面可以使观测器的阻尼最佳。

2.2 参考值优化算法

钻头和岩石间的摩擦力是变化的,并且难以直接测量。如果顶驱的电机不能提供足够的驱动扭矩克服比较大的非线性摩擦扭矩,提出的一些控制方案可能会失效。为解决这一问题,本文提出基于参考值优化的控制方案。可以根据当前的非线性摩擦力矩Tf和输入参考值ωref,实时优化设定各个状态的参考值xref,计算驱动扭矩的参考值Tem,使闭环控制系统处于最佳工作状态。

理想状态下,没有发生黏滑振动(或黏滑振动被抑制)时,系统(3)可以被表示为

0=Ax+BTm+DTf

x1=Cx

(6)

根据理想状态(6),可设计优化算法

(7)

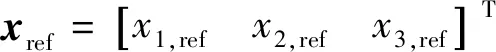
(8)

公式(8)恒成立,设计的参考值优化算法具备可行性。

由钻井参数和公式(7)可计算各个状态的参考值xref和前馈控制指令Tem

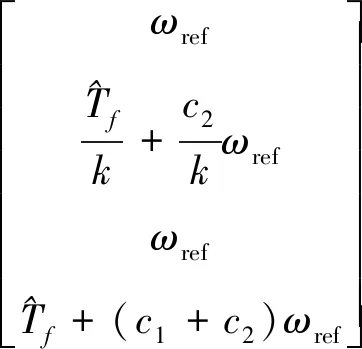
(9)

由公式(9)可知,被优化的状态参考值x1,ref=x3,ref=ωref。

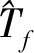
2.3 全维状态控制器

由于状态观测器(4)可以估计所有的系统状态x,参考值优化算法(7)可以获取各个状态的参考值xref,全维状态反馈控制器得以实现。为增强闭环系统抗干扰能力,参考值优化算法(7)同时设定驱动扭矩Tem。基于状态观测器(4)和参考值优化算法(7),设计了状态反馈和扭矩前馈相结合的全维状态控制器,其控制律

(10)

全维状态控制器(10)的扭矩前馈控制可以增强闭环控制系统抗外部干扰能力。全维状态控制器(10)的状态负反馈控制可以改变系统(3)的极点位置,增强闭环控制系统的动态响应。根据极点配置定理[12],若系统(3)完全可控,则配置闭环极点一定可使闭环控制系统稳定。

构造能控性判别矩阵

Q=B|AB|A2B

(11)

该矩阵的行列式

(12)

实际系统中CC2≤kJ2,则能控性判别矩阵的秩:

rank(Q)=3

(13)

可知系统(3)完全可控。因此,配置闭环极点一定可使闭环控制系统稳定于平衡状态

(14)

3 仿真分析

利用MATLAB,完成了对钻进系统双自由度集中参数模型(1)(或者(3))和状态观测器(4)的仿真,介绍了参考值优化算法(7)的功能,分析了全维状态控制器(10)的动态性能和克服摩擦力的性能。钻柱模型力学参数主要来源于文献[5,8]。

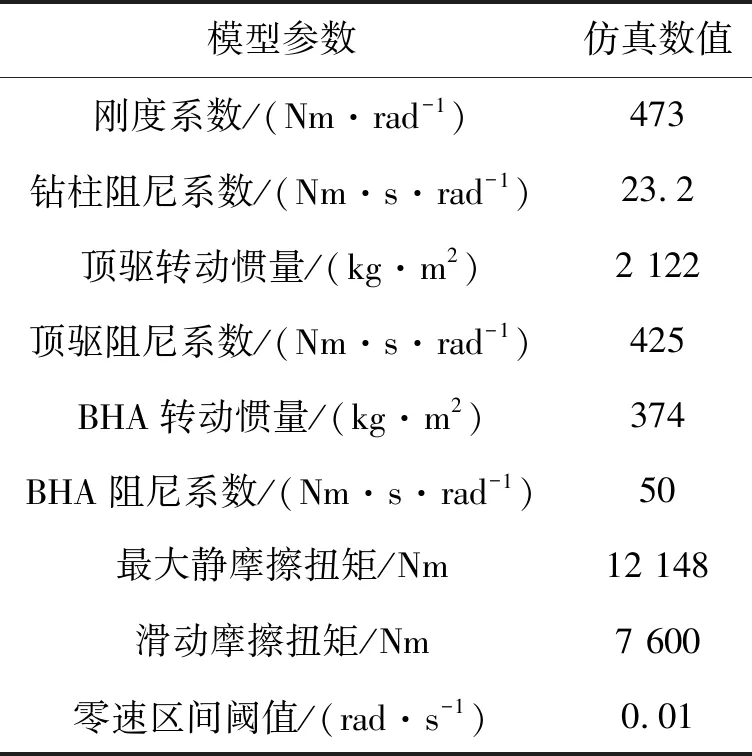
表1 钻柱模型力学参数

3.1 状态观测器性能分析

根据最优阻尼原理计算,参数特征比Di=0.5(i=2,3,4),时间常数T=0.3 s,状态观测器的增益Ko=[25.74,-113.22,8 364.14,-12 906 606]。为产生黏滑振动,仿真中系统输入设定为Tm=12 000 Nm。

钻柱黏滑振动发生时,双自由度集中参数模型(1)与状态观测器(4)的仿真结果如图3～图5所示。图3为钻头转速ω2的仿真值和估计值。从图3中可以看到明显的钻柱黏滑振动现象,钻头“黏滞-滑动-黏滞”周期性地交替。因此,双自由度集中参数模型(1)可以应用于钻柱黏滑振动机理的研究及黏滑振动控制方法的研究。

图4为顶驱与钻头角间位移差φ1-φ2的仿真值和估计值。角位移差的大小代表了钻柱储存能量的大小,是一个重要的参数,但是现有的其他研究中并不重视控制角位移差的大小。由图3与图4仿真结果可知,设计的状态观测器(4)可以比较准确地估计井下钻进系统的状态。因此,状态观测器(4)可以应用于诊断钻柱黏滑振动是否发生。

图5为非线性摩擦扭矩Tf的仿真值和估计值。图5表明,状态观测器(4)还可以比较准确地估计非线性摩擦扭矩Tf。现有的研究还有没涉及对非线性摩擦扭矩的估计。非线性摩擦扭矩估计值Tf为参考值优化算法提供输入。

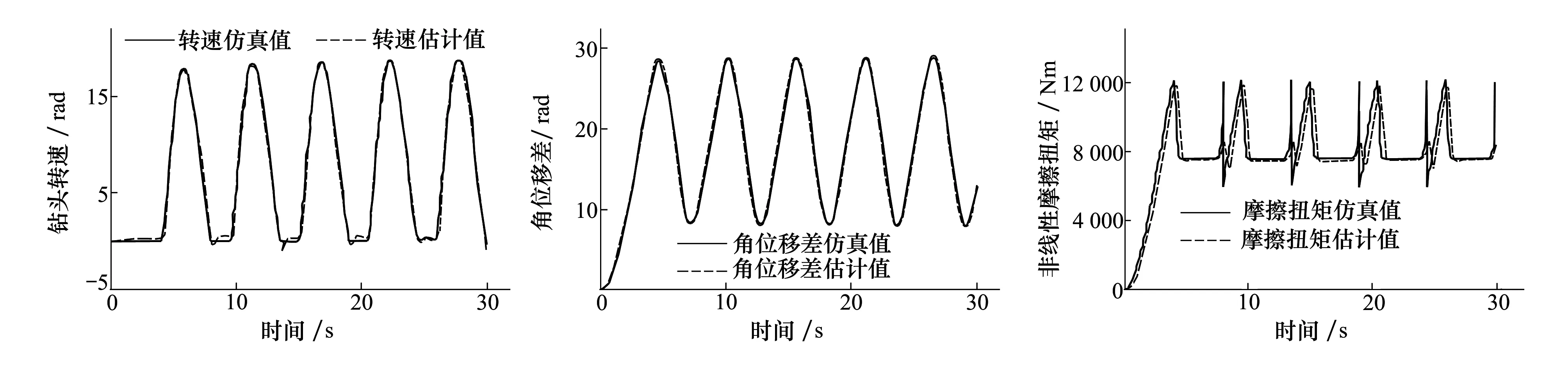
图3 钻头转速的仿真值x3与估计值 图4 角位移差的仿真值x2与估计值 图5 非线性摩擦扭矩的仿真值Tf与估计值

3.2 参考值优化算法功能分析

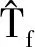
由公式(9)可知,状态参考值xref中,顶驱转速参考值x1,ref和钻头转速参考值x3,ref恒等于系统输入参考值ωref。图6与图7分别表示,在钻柱黏滑振动被抑制时,不同钻压下(WOB分别为100 kN,140 kN,180 kN),由参考值优化算法(7)获得的角位移差参考值x2,ref和前馈驱动扭矩的参考值Tem。由图6与图7可知,当钻头与岩石间的摩擦力(WOB)增大时,所需的驱动扭矩也会增加,并且顶驱与钻头间的角位移差也会增加。这意味着,外部扰动增大时,顶驱的有功功率增加,钻柱存储的能量增加。仿真结果表明,参考值优化算法(7)可以根据当前摩擦扭矩的大小,实时计算系统所需的驱动扭矩和系统状态的参考值。

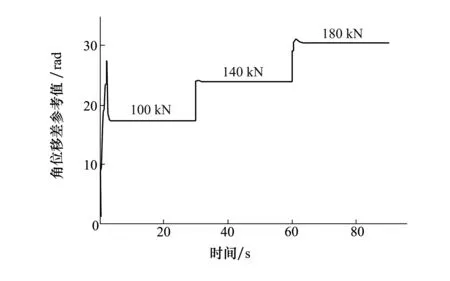
图6 不同钻压下角位移差参考值x2,ref

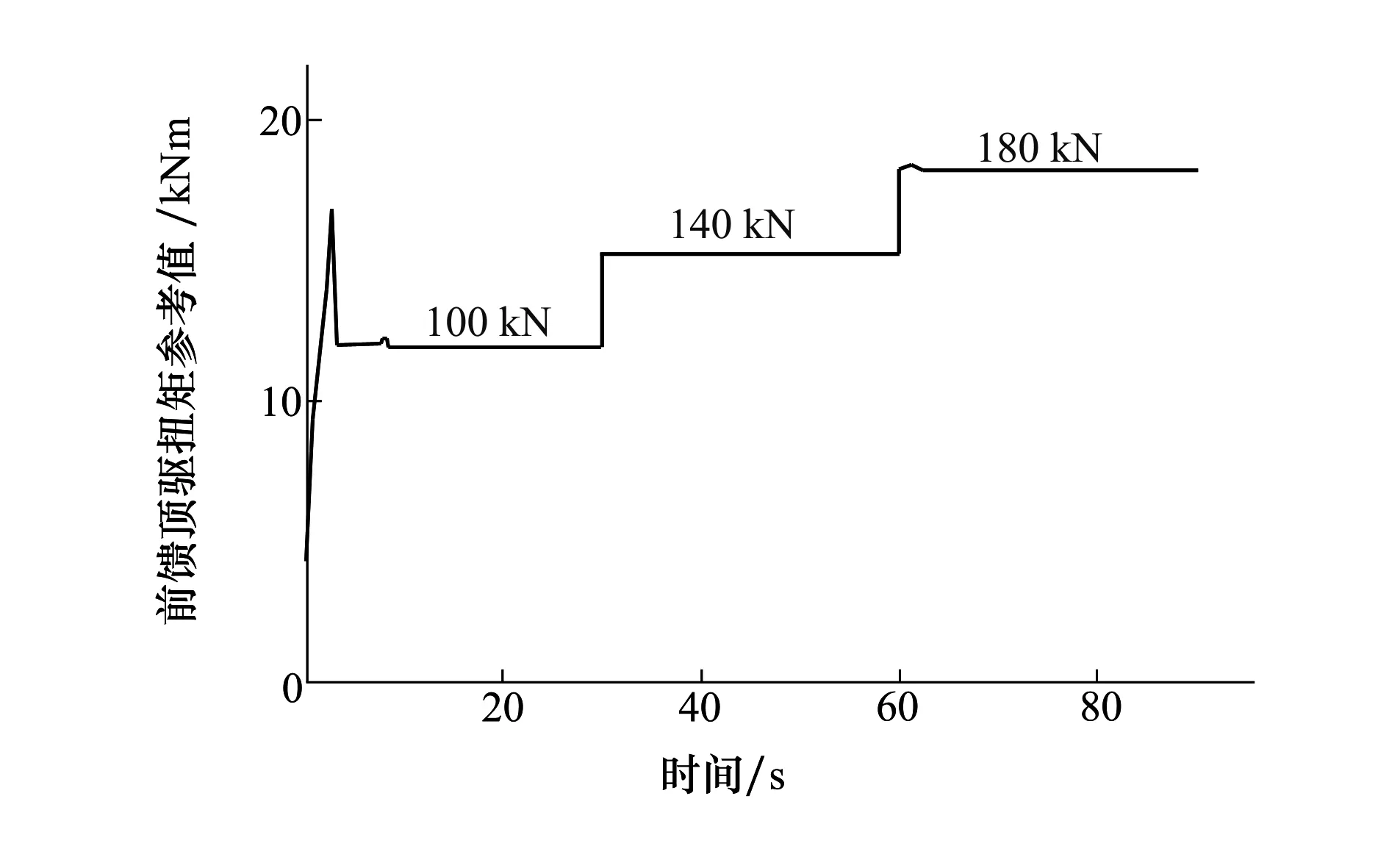
图7 不同钻压下驱动扭矩的参考值Tem

3.3 全维状态控制器性能分析

状态观测器(4)可以估计所有的钻进系统变量,参考值优化算法(7)可以获取各个状态的参考值和驱动扭矩。基于(4)和(7),设计全维状态控制器(10),并完成控制系统的仿真。根据最优阻尼原理,时间常数T=1.2 s,控制器(10)的增益[20 356,45 102,99 928,262 165]。为分析控制器(10)性能,本文引入钻井现场抑制钻柱黏滑振动常用的PI控制器进行对比。由于受到未知状态变量的限制,PI控制器只有一项反馈回路,其控制律

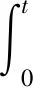
(15)

文献[2,13]也对PI控制器抑制钻柱黏滑振动的控制性能展开讨论。在仿真中,根据最优阻尼原理,PI控制器(15)的增益为[Kp=1 821,KI=1 322]。PI控制器(15)的输入参考值与控制器(10)的控制输入参考相同,为顶驱转速ωref=8.9 rad/s。

在不同的钻压下(WOB分别为100 kN,140 kN,180 kN),2种控制器控制效果的仿真结果(钻头转速响应)如图8～图10所示。仿真结果表明,在摩擦力比较小的情况下,PI控制器(15)与全维状态控制器(10)均可以抑制钻柱黏滑振动。与PI控制器(15)相比,全维状态控制器(10)的调节时间更短,超调更小,动态性能更加优越。当钻压(WOB)增加时,PI控制器所组成的闭环系统振动会更加强烈。并且当钻压增加到180kN时,PI控制器无法完成对钻柱黏滑振动的抑制,钻柱黏滑振动重新被激励。但是,即使钻压增加到180kN,提出的全维状态控制器(10)依然有效地抑制钻柱的黏滑振动。

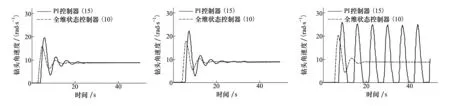
图8 钻压100 kN时2种控制 图9 钻压140 kN时2种控制 图10 钻压180 kN时2种控制 方案的控制曲线 方案的控制曲线 方案的控制曲线

4 井场实验

为了验证设计的控制方案对钻柱黏滑振动的抑制效果及其实用性,进行了井场实验。为防止控制器输出异常,对顶驱扭矩做限幅处理。

实际系统中,系统输入参考值ωref由操作员通过司钻箱设定(或者在电控房的变频器面板设定)。系统输入参考值大概ωref=95 r·min-1(实际系统中的钻柱侧数据),钻井压力WOB约100 kN,实时钻井深度约为3 000 m。所使用钻杆的内径为85 mm,外径为107 mm。顶驱转动惯量(转换到钻柱一侧)J1=1 473 kg·m2,钻柱的刚度系数约为k=205 Nm/rad,钻柱阻尼系数约为c=18.5 Nms/rad,井底钻具组合转动惯量约为J2=203 kg·m2。假定顶驱阻尼系数和井底钻具组合阻尼系数为零。这样会增加控制难度,但是如果在无阻尼条件下黏滑振动被有效抑制,则设计的控制器有更强的鲁棒性。

监测到的顶驱扭矩实际值如图11所示,监测到的顶驱转速实际值和通过状态观测器估计的钻头转速如图12所示。实验数据表明,在开启控制器之前,顶驱转速小幅度振动,约为95 r/min;顶驱扭矩发生剧烈波动,波动范围6 000～22 000 Nm;钻头转速出现零值,即发生钻柱黏滑振动。开启控制器后,经过调节之后,顶驱扭矩的振动被有效抑制,钻头转速的振动被有效抑制,并且钻头转速逐渐趋近于顶驱转速,围绕系统输入参考值小幅度振动。实验结果表明,钻柱黏滑振动得到有效抑制。

由现场实验可知,所设计的控制方案可以应用于抑制钻井现场产生的钻柱黏滑振动。

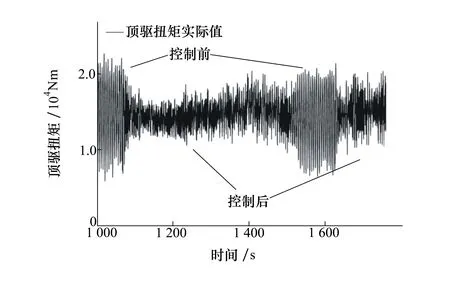
图11 监测到的顶驱扭矩实际值

图12 钻头转速估计值与监测到的顶驱转速实际值

5 结 论

文章构建了钻进系统双自由度集中参数模型,实现了对钻柱黏滑振动变化规律的特性仿真。基于提出的状态观测器和参考值优化算法,设计了一种状态反馈和扭矩前馈相结合的控制器。仿真结果表明:

1) 提出的状态观测器不仅可以比较准确地估计井下钻进系统的状态,而且可以估计钻头和岩石间的非线性摩擦扭矩,诊断钻柱黏滑振动的发生;

2) 根据估计的摩擦扭矩和顶驱目标转速,参考值优化算法可以实时计算系统所需的驱动扭矩和系统状态的参考值;

3) 与PI控制器相比,设计的全维状态控制器有效地抑制钻柱的黏滑振动并且拥有更好的动态特性和克服非线性摩擦的能力。

将设计的控制器应用于实际钻进系统并有效地抑制了钻井现场产生的钻柱黏滑振动。