满足增益相位裕度的自动驾驶仪结构化H∞综合

马晓川, 闫杰, 符文星, 陈康

(西北工业大学 航天学院, 陕西 西安 710072)

乘波体气动布局的高超声速飞行器通常没有翼面,升力主要由机体产生。由于乘波体布局头部的倾斜面设计结构,飞行器的气动压心相对于传统飞行器更靠机身头部,降低了飞行器的静稳定性,所以乘波体构型的高超声速飞行器一般具有静不稳定特性[1-2]。尤其高超声速飞行器进行大过载机动时,随着攻角增大,飞行器静不稳定度进一步降低[3-4]。对于静不稳定的高超声速飞行器,过大或过小的控制器增益都会引起飞行控制系统发散。因此在设计飞行控制器时,控制系统幅值增益在增大和减小2个方向上都要留有充分的稳定裕度,增加了控制系统的设计难度。

在复平面内考虑一个以实轴对称且包含(-1,j0)的圆,圆心和半径由控制系统期望的开环幅值裕度和相位裕度决定。当控制系统开环Nyquist曲线与圆没有交点时则认为控制系统满足期望的稳定裕度[5]。对于静不稳定被控对象,满足稳定裕度的控制器使开环控制系统的Nyquist曲线围绕圆一周或者多周且与圆没有交点,保证了控制器开环增益在增大和减小2个方向上都可以满足期望的裕度。基于此思想,文献[6]给出了一种基于H∞综合求解满足稳定裕度控制器的方法。此方法中控制系统的稳定裕度是通过约束标称系统增益放大后补灵敏度函数的H∞范数而实现的,求解控制器过程比较复杂,并且求解的控制器阶次比较高[7]。为了解决这些问题,本文使用结构化H∞综合方法,求解满足稳定裕度约束的控制器。

结构化H∞和H∞综合的区别在于使用结构化H∞综合算法求解控制器时,需要先定义控制器结构,例如PID控制器、三回路过载跟踪自动驾驶仪等[8-9]。控制器结构确定后,控制器中未知的部分只有控制器参数。控制器参数优化时与传统H∞综合相似,需要根据控制目标建立性能指标,并求解使性能指标H∞范数最小的控制器参数。因为控制器结构可以事先定义,结构化H∞综合算法使H∞控制理论具有了更好的实用性[10-14]。

本文以三回路过载自动驾驶仪为控制器结构,使用结构化H∞综合算法求解满足性能指标H∞范数最优的控制器参数,而且保证开环系统满足给定的幅值裕度和相位裕度。

1 结构化H∞控制

标准的H∞控制模型:

(1)

Z(s)表示评价系统性能的输出,Y(s)表示传感器测量输出量,W(s)为外部输入,U(s)是控制输入。假设存在反馈控制器C(s),系统的闭环传递函数可以表示为控制器C(s)的线性分式变换:

Tzω=Fl(P,C)=P11+P21(I+CP22)P12

(2)

标准的H∞控制问题是求解使系统(1)内稳定且保证Tzω(s)的H∞范数最小的控制器C(s)。与标准H∞控制不同的是结构化H∞综合需要预先设计好控制器C(s)的结构,例如PID控制器、校正网络、多回路自动驾驶仪等或者其他任意形式的控制器。控制器的结构具有任意无限多个,此处用PID控制器为例进行解释,典型的PID控制器为

(3)

PID控制器可以表示成控制器参数kp,kd,ki的线性下分式变换

CPID(s)=Fl(Q(s),K)

(4)

Q(s)是控制器中除去控制器参数的部分,K是由控制器参数组成的矩阵。把(4)式代入(2)式中,可得到闭环系统关于控制器参数的下分式变换

(5)

M(s)是被控对象和控制器开环传递函数除去控制器参数的部分。在结构化H∞综合中,控制问题就转换成求解使系统(1)内稳定且‖Tzω(s)‖∞最小的一组控制器参数。结构化H∞控制把经典H∞控制器求解问题转变为控制器参数优化问题[15-17]。另外与H∞综合不同,在结构化H∞综合中,性能指标可以是相互独立的,即性能指标可以表示为[8-9]:

H(s)=diag([T1(s),T2(s),…]T)

(6)

diag(T)表示由向量T中元素组成的对角矩阵。这一特性使得结构化H∞综合算处理多目标约束优化问题更为方便。

2 增益裕度和相位裕度

在复平面内考虑一个包围点(-1,j0),以(-a,j0)为圆心,r为半径的圆O,如图1。当控制系统开环Nyquist曲线不与圆O相交时,控制系统至少具有幅值裕度

Gm1=-20lg(a-r)

(7)

Gm2=-20lg(a+r)

(8)

相位裕度:

(9)

公式(7)Gm1由点A到(-1,j0)的距离计算得出,若系统开环增益放大倍数小于Gm1dB,闭环系统依然稳定;公式(8)Gm2由点B到(-1,j0)的距离计算得出,若系统开环增益减小倍数小于Gm2dB,闭环系统依然稳定。公式(9)表示圆O与单位元交点C与原点的连线和实轴的夹角,表示开环系统的相位裕度。图1以圆心在(-1,j0),半径r为0.5的圆O为例进行解释说明。圆O与实轴相交于点A(-0.5,j0)与点B(-1.5,j0),圆O与单位圆交点连线和实轴夹角为29°。系统开环Nyquist曲线与圆O没有交点时,对于静稳定被控对象系统至少具有6 dB的幅值裕度和29°的相位裕度。对于静不稳定被控对象,系统至少具有±6 dB的幅值裕度和29°的相位裕度。

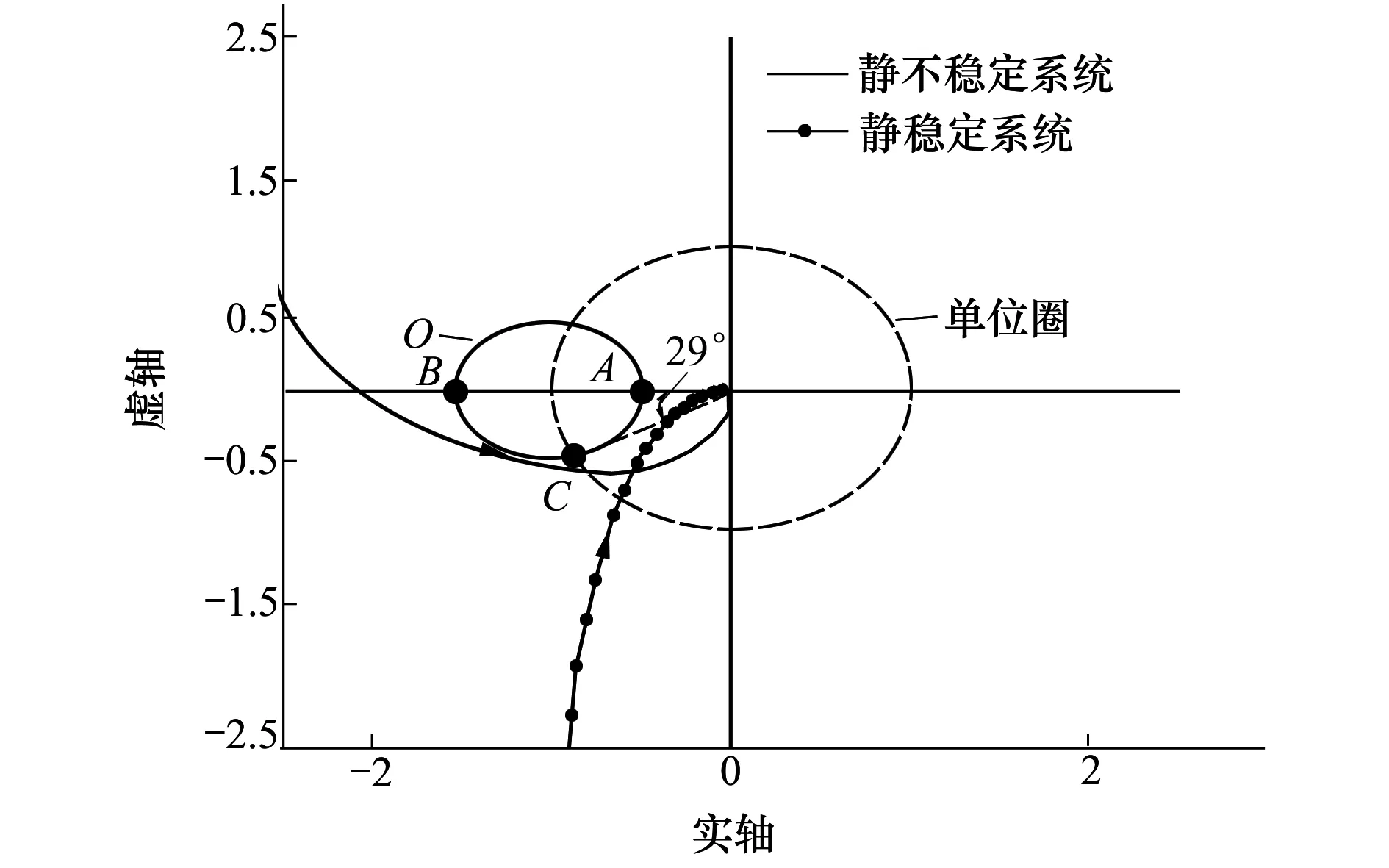
图1 系统增益裕度和相位裕度

控制系统开环Nyquist曲线不与圆O相交等价于

P(jω)C(jω)≠(-a+rexp(jθ))

(10)

方程(10)中C(jω)是控制器,P(jω)为被控对象。对方程(10)进行变换

(11)

方程(11)可以表示成如下形式[6]

[A+Rexp(jψ)]P(jω)C(jω)≠1

(12)

式中

(13)

A+Rexp(jψ)可以看作标称被控对象P(jω)的乘性不确定性加权(A+ΔR),其中‖ΔR‖∞=R。

根据小增益定理,使图2表示的闭环控制系统鲁棒稳定的充要条件是

(14)

不等式(14)等价于

(15)

不等(15)式左边括号中的部分可以看作标称系统P(s)乘以放大系数A后的闭环补灵敏度传递函数。当不等式(15)成立时,系统P(s)C(s)的Nyquist曲线不与圆O相交,即开环控制系统P(s)C(s)满足至少由(7)～(9)式表示的稳定裕度。

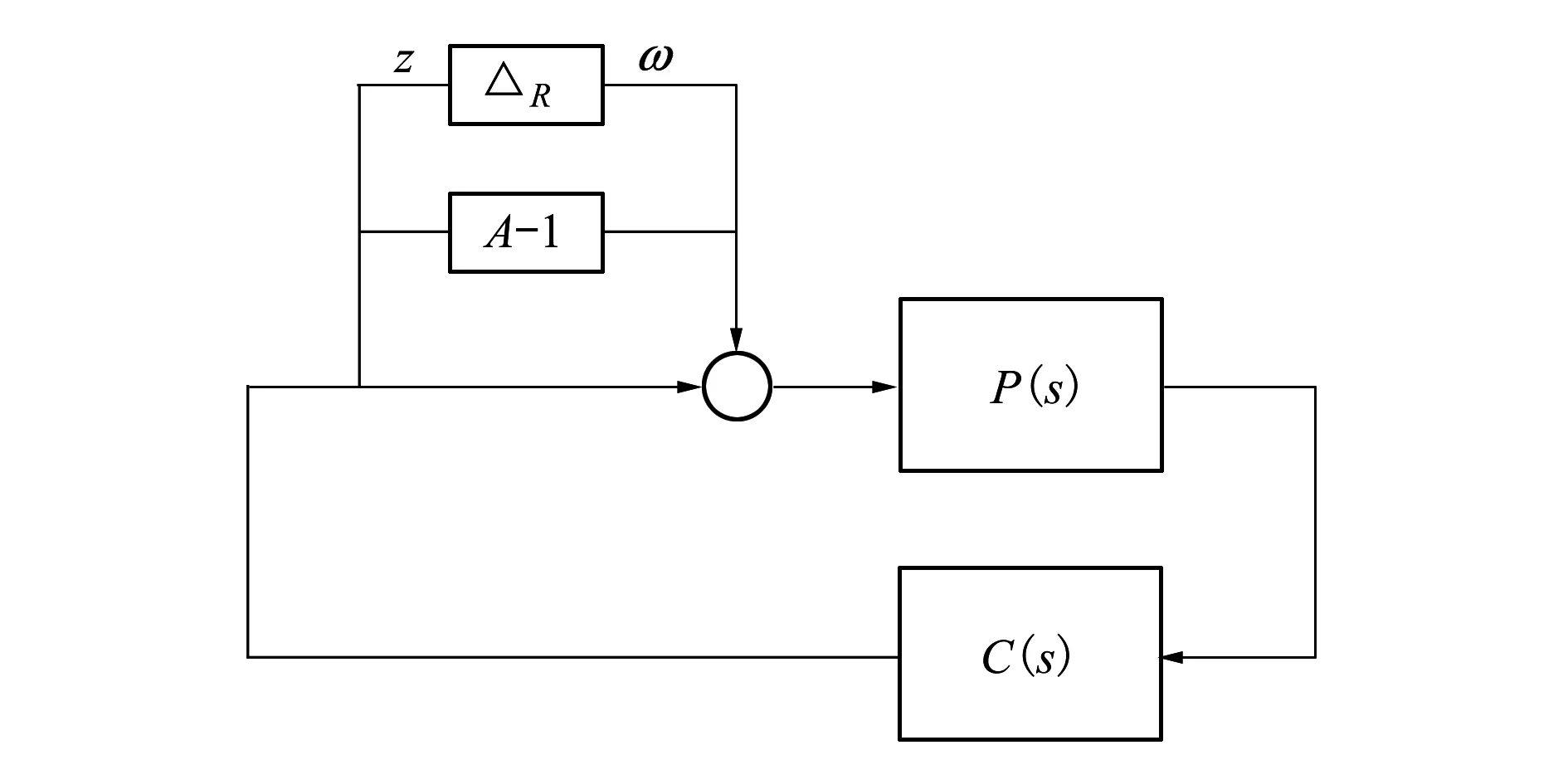
图2 带有乘性不确定性的闭环控制系统

对被控对象P(s)设计满足预定稳定裕度的控制器问题可以表示为在AP(s)加权补灵敏度函数的H∞范数小于1的条件约束下,求解稳定控制器C(s),使性能指标的H∞范数最小:

(16)

式中

Tn(s)=[T1(s),T2(s),…]T

(17)

表示对闭环系统性能约束的传递函数。

Wn(s)=diag([W1(s),W2(s),…])T

(18)

是相应的加权传递函数。

(19)

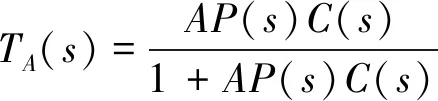
(20)

上述是带有不等式约束的H∞优化问题,直接求解比较困难。因为结构化H∞综合可以解决性能指标相互独立的约束问题,所以在Wn(s)中加入调节参数η,此时求解满足稳定裕度控制器的性能指标传递函数可表示为

(21)

当使用结构化H∞综合求解出使(21)式H∞范数最小的控制器参数不满足(16)式中的不等式约束时,可通过调节参数η使其满足小于1的约束。

3 控制器设计及仿真

以文献[18]给出的COM高超声速飞行器模型为被控对象,使用结构化H∞综合设计过载跟踪自动驾驶仪,并保证自动驾驶仪稳定裕度满足给定要求。(22)式给出了COM在高度20 km,飞行速度10马赫时的线性化模型。

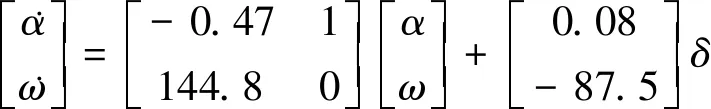
(22)

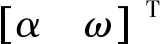
图3给出了闭环控制系统的结构示意图,图中控制器结构是典型的三回路过载跟踪自动驾驶仪。

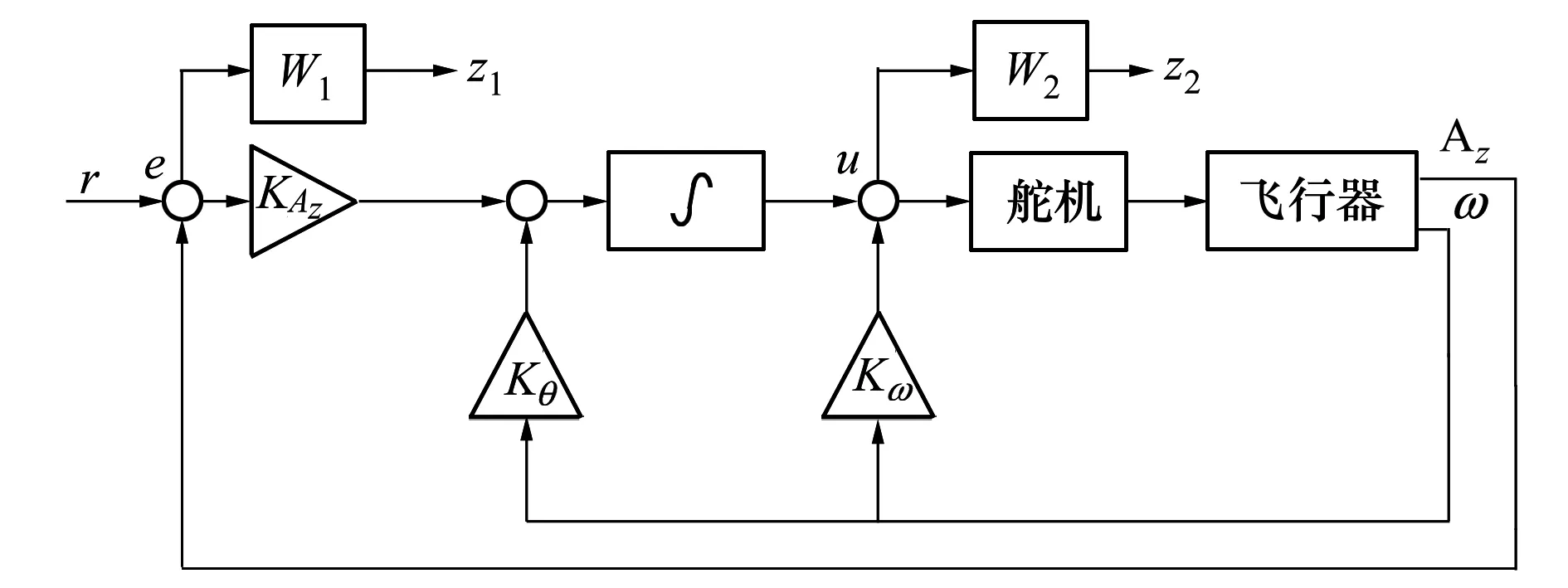
图3 闭环系统

其中KAz,Kθ,Kω是待优化的参数。r,e,u分别是参考输入、跟踪误差和控制器输出。z1和z2是描述系统性能的输出。

权函数W1用于约束系统跟踪误差和动态响应

(23)

权函数W2(s)对控制器指令输出进行约束

(24)

控制器要求至少有6 dB幅值裕度和36.9°的相位裕度。对应于复平面上约束稳定裕度的圆O,圆心在(-1.25,j0),半径r等于0.75。根据(13)式和(19)式得加权函数为

WA=0.6

(25)

控制器综合时使用的优化指标为

He=diag(W1T1,W2T2,WATA)

(26)

式中，T1是系统的灵敏度函数,T2是参数输入到控制器指令输出的传递函数,TA是开环系统增益放大补灵敏度函数,由(20)式给出。W2中的参数η用于调节‖WATA‖∞,使其满足(16)式的不等式条件。仿真中使用的是Matlab 2014中的hinfstruct()函数进行控制器综合。

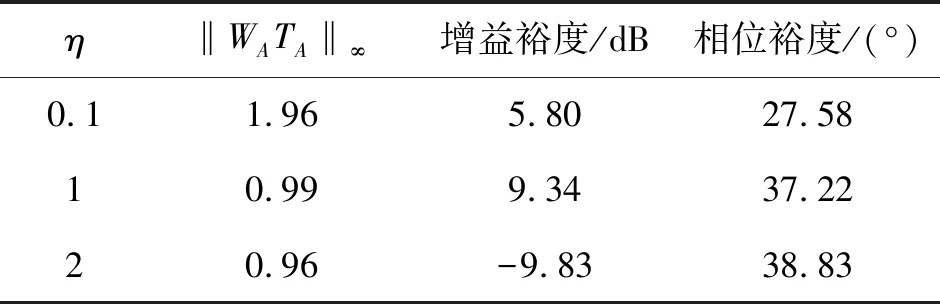
表1 控制器优化结果

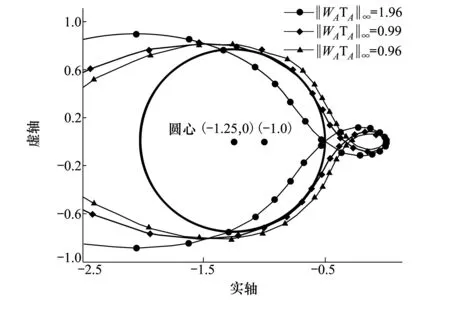
图4 开环Nyquist曲线

表1中给出了选取不同η时使用结构化H∞综合的结果。图4给出了相应η值时系统的Nyquist曲线。系统的断开点选取在控制器输出端,即图3中舵机与邻近的求和点中间。为了能更清晰地表明系统Nyquist曲线与圆O的关系,图中省略了低频部分的Nyquist曲线。表1中的结果显示,不同的η会影响综合后的‖WATA‖∞。而图4表示了‖WATA‖∞数值与圆O的位置关系。当‖WATA‖∞大于1时,系统的Nyquist曲线与圆O相交,此时不能保证系统具有要求幅值与相位裕度。需要强调的是系统Nyquist曲线不与圆O相交是满足增益与相位裕度的充分条件,而非必要条件。所以当‖WATA‖∞大于1时系统仍有可能满足增益相位裕度要求。因为增益相位裕度定义中要系统开环Nyquist曲线上相位为180°和幅值为1的2个点到点(-1,j0)的距离大于裕度要求。而本文通过限制Nyquist曲线到描述稳定裕度圆的距离方法来使控制系统达到增益相位裕度。这不仅要求Nyquist曲线上相位为180°和幅值为1的2个点到点(-1,j0)的距离要满足预定条件,而且其他的点到点(-1,j0)距离也需要满足预定条件。这种限制条件比稳定裕度定义更苛刻。但当‖WATA‖∞小于1时,系统Nyquist曲线与圆O相切或不相交,此时一定可以保证系统满足稳定裕度要求。表1中稳定裕度计算结果表明系统增益裕度大于6 dB,相位裕度大于36.9°,控制器的稳定裕度满足预定条件。另外,表1中增益裕度-9.83 dB表示当开环增益减小9.83 dB会引起闭环系统发散。

图5和图6给出‖WATA‖∞不同时系统的过载跟踪响应。当‖WATA‖∞大于1时系统的稳定裕度较低,响应过程中发生轻微的震荡。当‖WATA‖∞小于1时系统响应比较平稳。从响应速度上分析,当满足稳定裕度要求时,‖WATA‖∞越接近1系统的响应速度越快,保守性越小。所以需要确定η使‖WATA‖∞等于1。从图7中可以看出随η增加的过程中‖WATA‖∞单调减变化且‖WATA‖∞与1有一个交点。所以可以使用二分算法确定使‖WATA‖∞等于1的η。

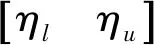
1)η=ηl

2) 使用结构化H∞求解使(22)式最小的控制器参数

3) if ‖WATA(s)‖∞=1

迭代结束

else

if ‖WATA(s)‖∞<1

else

返回执行步骤2)

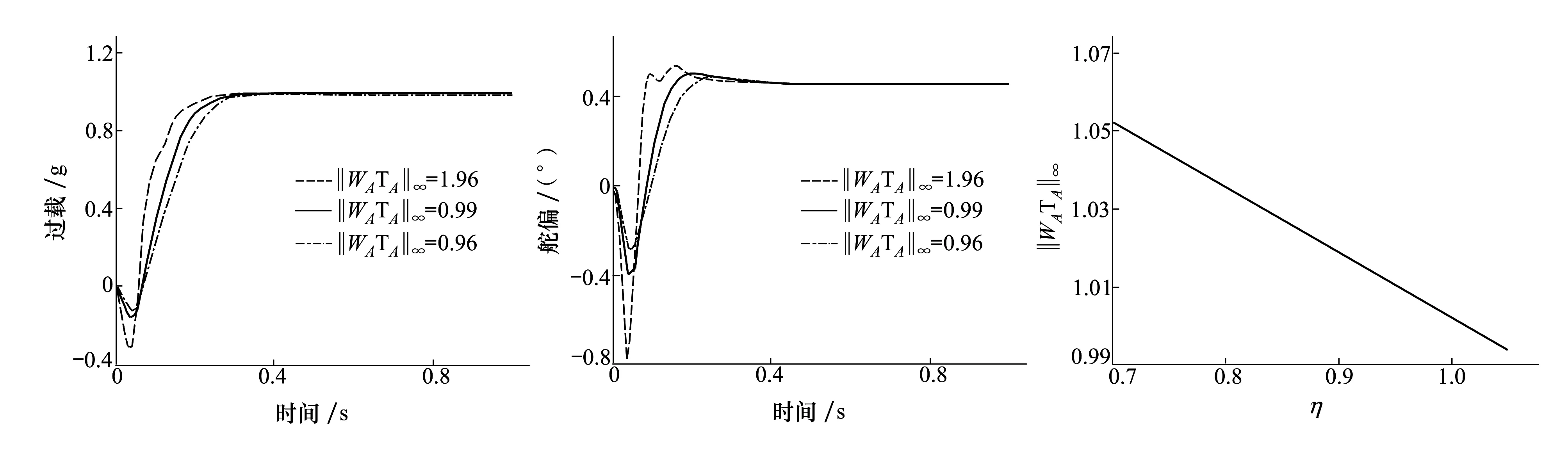
图5 单位过载响应 图6 舵响应图7 ‖WATA‖∞曲线

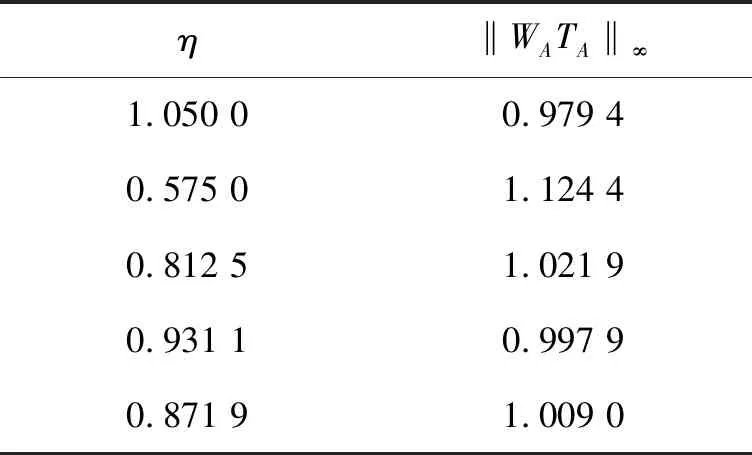
表2 迭代计算结果

表2给出了迭代计算中部分结果,当η等于0.871 9时,‖WATA‖∞为1.009 0。如图8所示,系统的Nyquist曲线与圆O相切,此时系统的稳定裕度为9.18 dB和36.9°,满足预先设定的要求。

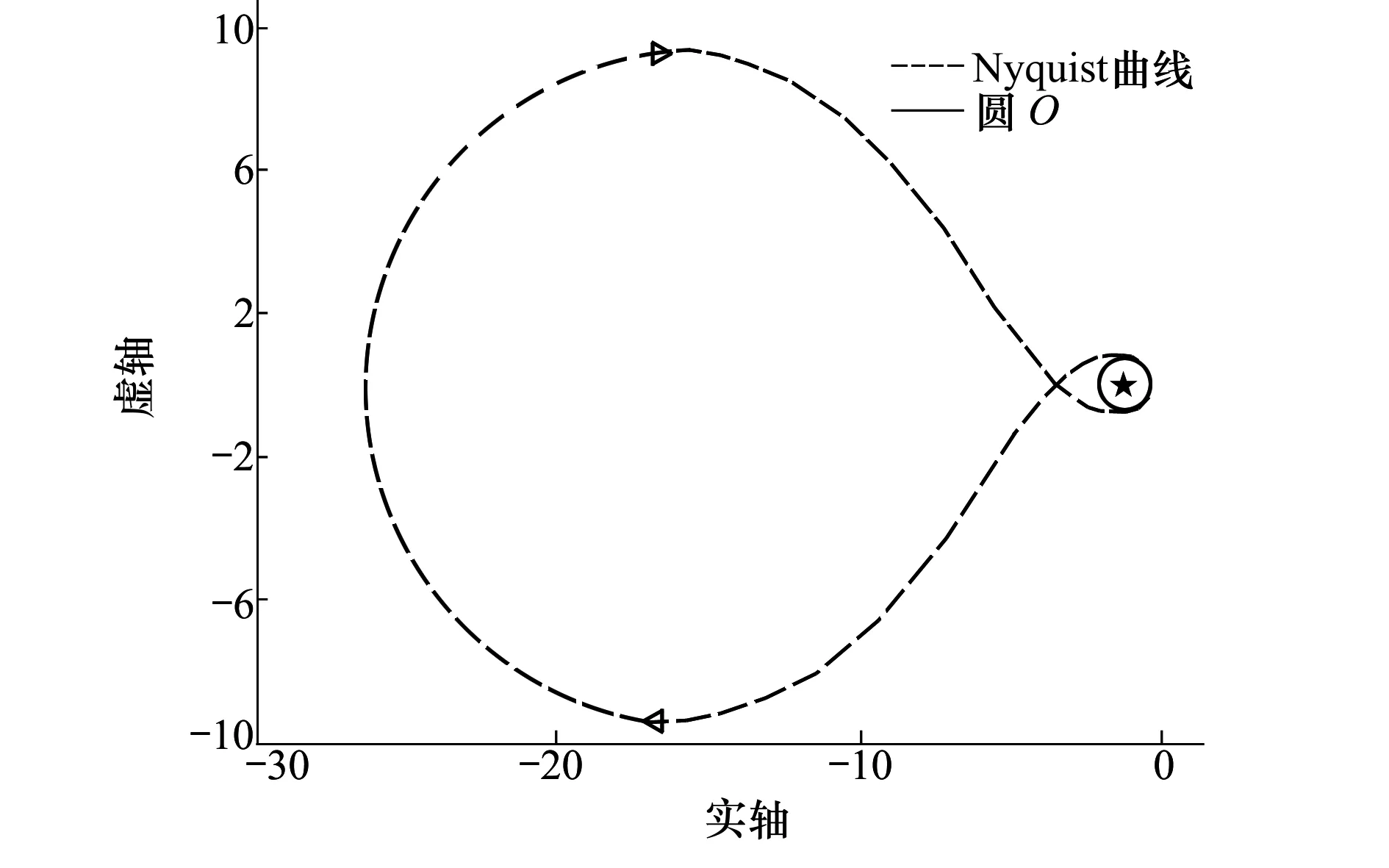
图8 Nyquist曲线

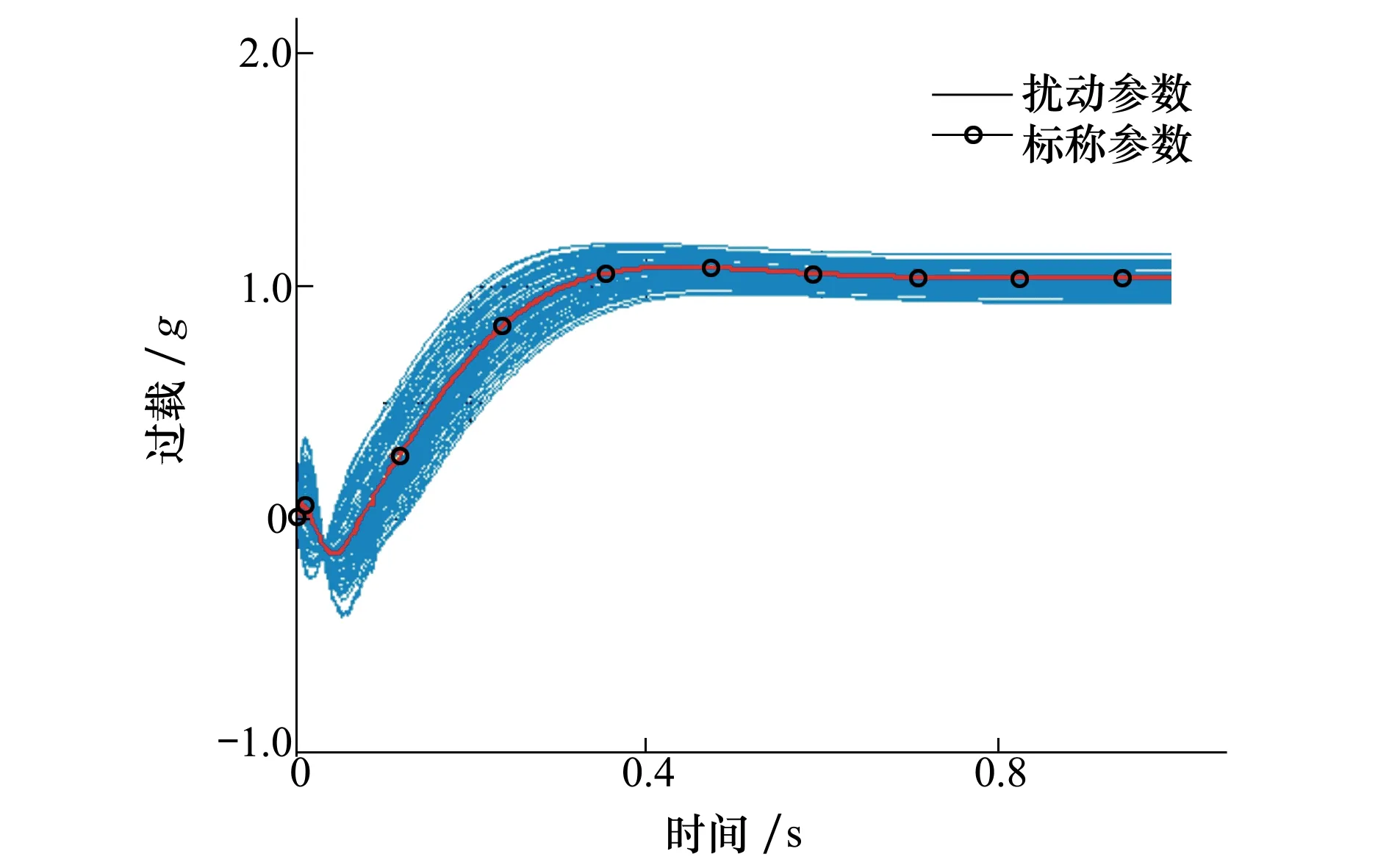
图9 气动参数扰动条件下过载跟踪响应

为了验证控制方法对非线性系统的适应性和鲁棒性。在仿真中使用文献[18]提供的非线性高超声速飞行器模型数据进行计算。计算过程中考虑气动力系数和气动力矩系数±10%以内的随机扰动。使用非线性模型在气动参数扰动的条件下,进行了100次的单位过载跟踪仿真实验。图9中的曲线是仿真计算结果。结果表明无论对标称非线性模型还是气动参数扰动模型,控制系统都能稳定完成对单位过载指令的跟踪。但因为模型非线性和气动参数扰动的影响,过载跟踪精度有所下降。

4 结 论

对于静不稳定的高超声速飞行器,本文使用结构化H∞综合方法设计了飞行器的过载跟踪自动驾驶仪。通过调节优化结果中增益放大系统补灵敏度函数的H∞范数,改变系统Nyquist曲线与复平面内表示稳定裕度圆盘的相对位置,使控制器满足稳定裕度要求。并给出了计算使系统Nyquist曲线与圆盘相切的控制器参数计算方法,以减小控制器设计的保守性。计算仿真结果表明:

1) 由文中控制算法设计的自动驾驶仪能达到预定增益相位裕度指标要求;

2) 在控制器综合时,调节性能指标中引入的参数η能改变开环Nyquist曲线与表示稳定裕度圆盘的相对位置,并改变系统的保守性;

3) 由文中控制算法设计的自动驾驶仪可以使用在非线性系统上,并且控制系统对参数扰动具有鲁棒性。