基于距离测量的多无人机协同目标定位方法

屈耀红, 张峰, 谷任能, 袁冬莉

(西北工业大学 自动化学院, 陕西 西安 710072)

战场目标的精确定位是现代化战争中的关键技术之一[1]。随着无人机技术的快速发展，利用多架无人机协同对目标定位，已成为当前军事科技领域的研究热点[2]。

目前，由于无线电测距技术发展成熟，其精度高且成本低，因此基于距离测量的目标定位方法的研究受到了普遍关注。文献[3]提出了一种基于约束总体最小二乘(constrained total least-squares,CTLS)的固定观测站时差定位算法(time-difference-of-arrival,TDOA)，在忽略观测站坐标误差时，其定位精度较高，但若观测点坐标测量存在随机误差时其定位性能急剧下降。文献[4]提出了一种线性校正到达时间差的定位算法，在假设传感器位置信息精确已知的条件下，该方法可以获得很精确的定位结果，但如果传感器位置信息存在随机误差，该方法就会严重降低目标的定位精度。文献[5]提出利用斜距离解析目标位置的定位方法，同样，该方法并未考虑观测机的坐标测量误差，当该误差较大时，其定位性能急剧下降。

另外，几何定位精度因子(geometric dilution precision,GDOP)是衡量一个定位系统精度的重要指标之一，其取值与各观测点之间不同的几何分布相关[6]。

综上分析，本文提出了一种利用多无人机与目标之间的距离以及无人机站址坐标估算目标位置的协同定位算法，该方法克服了站址误差不可忽略时定位效果急剧下降的不足，同时，利用GDOP优化了编队队形，进一步提高了定位效果。受到了参考文献[7]的启发，本文提出的方法同时保证了较高的定位精度和较强的适应性。

1 定位模型及定位方法

1.1 定位条件

如图1所示，至少需要3架无人机来对目标进行协同定位。假定每个无人机均装备有GPS和测距传感器，并围绕同一个目标飞行，目标大致位于编队中心点下方。无人机可利用GPS获得自身的位置坐标，利用测距传感器测量自身到目标的距离。考虑到信号时间的同步性，做出如下假设：

若目标为移动目标，在多架无人机进行定位作业之前，以机载GPS时钟信号为基准，完成3架无人机时钟初始校准；其次，将3架无人机获取的位置信息及距离信息标志时间戳，选取时间戳差值较小的3组数据，且假定目标移动较慢，即目标在信号偏差时间内的位移量可忽略；最后，利用选取时间戳相近的3组数据完成目标坐标解算。

若目标静止不动，则不需要考虑信号时间的同步性，利用3架无人机位置信息及距离信息，构成定位方程即可实现目标定位解算。

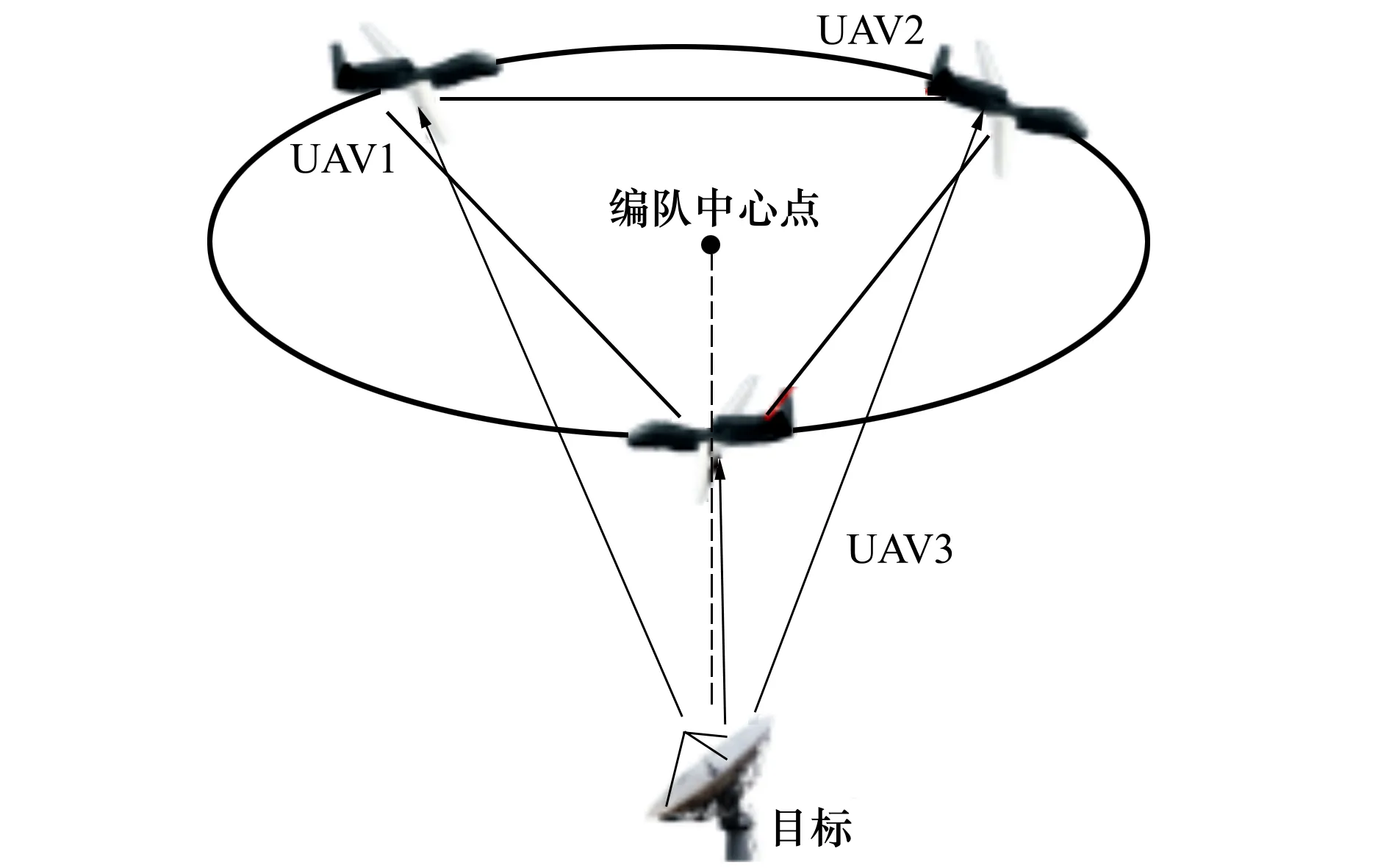
图1 多无人机协同定位实例

1.2 定位方法

本文提出的算法主要由三大部分组成：首先，利用传统距离定位算法求出目标的大致位置x0;然后,将距离测量的非线性方程在x0处一阶Taylor展开转化为量测距离信息加上无人机的站址误差以及测距传感器的测距误差信息方程,求出定位解的表达式;最后,求出定位解中参变量的值,完成目标位置的估算。接下来是对每个部分的详细介绍。

1.2.1 目标大致位置的求解

假定多机协同定位模型处于地心空间直角坐标系中,目标的真实坐标为xt=[xt,yt,zt]T,无人机观测站的坐标为xi=[xi,yi,zi]T,i=1,2,3。各无人机到目标之间的距离为

(1)

令

(2)

式中，r为目标所属区域与地球质心之间的距离,对(1)式平方并联立(2)式可以得到

(3)

即

至此,传统距离定位方程如(3)式所示,将其写为矩阵形式有

A1xt=B1

(4)

式中

计算上式,目标的大致位置x0为

(5)

将其作为Taylor展开点,完成后续的算法。

1.2.2 目标坐标的求解

引入测距误差信息(ερi)构建定位方程为

ρi=‖xi-xt‖+ερi,i=1～3

(6)

(7)

至此得到初步定位方程,写成矩阵的形式如下

Ay=B

(8)

式中:

类似于(4)式,可以求出初步定位方程的解

(9)

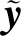
(10)

式中:

结合(10)～(14),可以得到误差方程为

(A-ΔA)y=(B-ΔB)

(15)

令

(16)

令

(17)

则有

A*y=B*

(18)

ΔA,ΔB可以表示为

(19)

令Hy=xG1+yG2+zG3-G4,其中(x,y,z)的值为初步定位方程的解y,目标的定位解为:

(20)

联立(19)、(20)式可得

(21)

为了求解yTLS,对(19)式求一阶导并运算可得

(22)

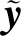
1.2.3 参数λ的求解

令

yTLS=y*+δy

(23)

即δy为真实值与定位解的差值,将(21)式代入(19)式可以得到δy的表达式

(24)

其均方误差为

(25)

参数λ的估计值为

(26)

定义

(27)

(28)

D=diag[(μ1+λ)-2,(μ2+λ)-2,(μN+λ)-2]

(29)

将(26)和(27)式代入(25)式可得

(30)

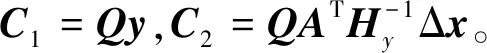
(31)

将(26)、(30)和(31)式联立得到参数λ为

(32)

根据参考文献[8],选取λ的值为

(33)

将参数λ的值代入定位解的表达式得到定位解为

(34)

1.3 几何精度因子(GDOP)的求解

从方程(10)可以得到

(35)

式中,ε为等效距离误差,δx=(δxt,δyt,δzt)为无人机站址误差,将(35)式展开

δρ=Hδx+ε

(36)

式中

近似地,可以得到

δρ=Hδx

(39)

对(39)式等号两边均左乘以H-1有

δx=H-1δρ

(40)

误差协方差为

E(δxδxT)=H-1E(δρδρT)(HT)-1

(41)

因为GDOP仅跟对角元素有关,可假设E(δρδρT)互不相关且方差相同均为1,则有

E(δxδxT)=(HTH)-1

(42)

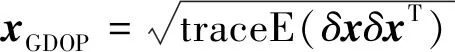
(43)

2 仿真实验

2.1 仿真条件

为验证所提定位方法的有效性及适应性,本文提出以下假设条件:

1) 3架无人机定高并围绕目标飞行,每架无人机的距离测量误差方差及站址测量误差方差满足如下关系:

2) 文中的坐标系统为WGS-84地心空间直角坐标系,坐标原点为地球质心。

2.2 仿真结果

2.2.1 定位算法的有效性及适应性分析

目标的真实位置为xtrue=(6 371,20,0.2),3架无人机的初始位置如表1所示,单位为km。基于本文提出的定位算法,令每次试验中站址量测误差取值于区间[0,0.01 km],目标的大致位置x0=[x0,y0,z0]T及目标的求解坐标xt=[xt,yt,zt]T如图2所示。

表1 无人机的初始位置

图2 目标的大致位置及定位解

随着站址误差的增大,目标的大致位置和求解坐标均不同程度的偏离真实坐标,显然,xt更接近真实位置;此外,即使目标的大致位置与真实位置偏差较大时,本算法依然能解算到较为理想的坐标。

为分析定位算法的有效性及适应性,将本方法与传统距离定位方法进行了两方面比较:当无人机观测站的站址误差可以忽略时,改变距离测量误差的取值,比较二者的定位精度,仿真如图3所示;此外,在距离测量误差不变的前提下,比较二者对于无人机站址测量误差变化的适应性,仿真如图4所示。

图3 定位误差随距离量测误差变化的比较图

如图3所示,随着距离测量误差的增大，本算法保持着较好的定位精度。显然,当无人机站址量测误差为零时,本算法具有较好的定位效果。从传统的距离算法可以清楚地看出,其定位精度受到地球半径精度的影响,在算法过程中引入了更多的误差。综上,本方法更具有效性。

将距离量测误差的值设为σ2=0.002 km,并引入无人机观测站的站址量测误差,2个算法的定位误差随站址量测误差变化的比较如图4所示:

图4 定位误差随站址量测误差变化的比较图

由图4可知,若站址量测误差不可忽略,显然本算法适应性更强,精度更高;结合图3与图4可以看出,本方法的定位精度明显优于传统定位方法。

2.2.2 无人机编队队形分析

选取最小GDOP对应的编队队形作为理想编队队形,以提高定位精度。基于图1所提出的多机协同定位模型,本文利用3架无人机的初始位置表示其组成的编队队形,编队队形的鸟瞰图如图5所示,多无人机定高并围绕目标飞行,其航迹共圆且目标位置的投影包含于圆中。基于1.3节所提出的GDOP的求解方法,利用在线枚举法将无人机编队的所有队形所映射的GDOP值求解并找出最小GDOP值所映射的编队队形。无人机的编队队形的表示如下:

图5 无人机编队队形鸟瞰图

1) UAV1和UAV2之间的距离d保持不变,UAV3的位置沿着航迹圆运动,得到d条件下的所有队形,如表2所示。

表2 d=1.8时无人机编队队形

2) 令d在区间(0,2r)中自小到大依次取值,同时,UAV3的位置沿着航迹圆运动,得到无人机编队的所有队形,如表3所示。

表3 无人机编队的所有队形

对表2所述的无人机队形进行GDOP求解,其仿真结果如图6所示。

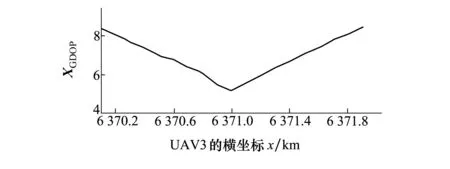
图6 GDOP随无人机编队部分队形变化图

如图6所示,GDOP的值随着UAV3横坐标x增大而先减小后增大,有一个明显的极小值,此时极小值所映射的无人机编队队形就是在d=1.8条件下的最优编队队形,该队形是由(6 370.1,19.5,1),(6 371.9,19.5,1),(6 371,21,1)这3个点所确定的一个锐角三角形。

对于如表3所述的所有的无人机编队队形,依次求解队形所映射的GDOP,结果如图7所示。

图7中GDOP有一个十分明显的极小值,位于d=1.71,x=6 371.2处,无人机编队的位置为：(6 370.145,19.481,1),(6 371.855,19.481,1),(6 371.2,20.980,1),即无人机的最佳编队队形为正三角形,其目标位于正三角形中心正下方附近时GDOP最小。

图7 GDOP随无人机编队的所有队形变化图

2.3 仿真结果分析

从图2可知，在不考虑无人机观测站的站址误差时，本文提出的定位方法效果优于传统距离定位算法。究其原因，传统距离定位方法精度受到地球半径精度的限制，引入了新的误差项。对比图2和图3可知，引入无人机站址误差后，传统方法的定位效果会差一些。综上，本方法具有良好的有效性和适应性。

基于本文所建立的多机协同定位模型，表述出3架无人机航迹共圆的所有队形，利用在线枚举法寻求最小GDOP值对应的编队队形，如图5～6所示，保持无人机编队队形为正三角形，尽量使无人机编队的中心在地面的投影靠近目标的位置，可提高目标定位精度。

3 结 论

本文提出了一种多机协同地面目标定位方法，综合考虑了无人机观测站的量测误差和距离测量误差，定位效果较传统的距离定位方法来说更好，通过仿真验证了其有效性和适用性。

对于本文所建立的多无人机协同定位模型，目标的位置处于正三角形的中心正下方附近，应保证编队队形为正三角形，以提高无人机定位精度。