基于地磁场自适应修正的航姿系统姿态解算研究

王录, 刘明雍, 王梦凡, 郭娇娇, 雷罡, 张小件

(西北工业大学 航海学院, 陕西 西安 710072)

随着微机电系统(MEMS)技术的高速发展,MEMS传感器(陀螺仪、加速度计和磁力计)在移动设备(智能手机、无人智能系统等)领域的使用越来越普及。虽然MEMS传感器的成本越来越低、集成度越来越高、体积越来越小[1],但是存在输出噪声过大、零点漂移无法完全消除、角速率输出易受干扰等问题,因此可以采用多个传感器通过信息融合算法[2]实现高精度的姿态解算。

针对AHRS传感器在姿态解算过程中,输出姿态存在噪声较大及累积误差等问题,文献[3]提出了一种基于四元数的互补滤波算法,对于由MEMS陀螺仪解算的具有较大累积误差的姿态四元数,首先利用重力加速度信息对载体姿态的横滚及俯仰分量进行修正,其次利用地磁场信息对载体航向分量进行修正。文献[4]设计了一种基于四元数的扩展卡尔曼滤波算法,该算法分别利用陀螺仪输出数据与加速度计输出数据构建状态转移矩阵与量测矩阵,不需求解雅克比矩阵,降低了构建基于姿态矩阵的扩展卡尔曼滤波算法的复杂性。文献[5]针对文献[4]中量测噪声协方差矩阵出现的奇异,加入了一个对角矩阵,有效克服了文献[4]所提出的算法在工程应用中的局限性。文献[6-7]提出的基于姿态矩阵的扩展卡尔曼算法利用重力加速度与地磁场矢量构建非线性量测方程,需要求解雅克比矩阵来获得量测矩阵,大大增加了该算法的运算量。文献[8]提出了一种通过利用扩展卡尔曼滤波器进行数据融合以获得姿态的准确输出,考虑加速度对系统精度的影响,解决了四元数协方差奇异性问题,其中的地磁场分量通过GPS测得的经纬度和世界地磁场模型求出。文献[9]提出了一种自适应卡尔曼滤波算法,该算法自适应估计加速度计量测噪声协方差矩阵,用于补偿载体在运动过程中产生的线性加速度误差。

本文针对:①当只利用加速度数据时,载体航向分量依然存在累积误差;②当加入磁力计数据时,由于环境对地磁场数据的影响极大[10],因此解算出的载体姿态对环境敏感,而且先验地磁场矢量未知等问题,提出了一种自适应的扩展卡尔曼滤波算法。首先由最小方差原则,利用加速度计数据对载体姿态的横滚及俯仰分量进行准确估计;其次在上述估计的基础之上,该算法结合磁力计数据对载体姿态的航向分量进行了修正。优点是在消除累积误差的基础上,能尽量降低姿态输出噪声,而且周围环境的磁扰动对载体横滚及俯仰分量不产生任何影响,仅对航向分量有一定的影响。

1 AHRS问题提出

本文提出的基于自适应扩展卡尔曼滤波器的AHRS姿态解算算法是在扩展卡尔曼滤波算法的基础之上,加入了实测地磁场信息,从而不断修正载体姿态的航向累积误差,如图1所示。

图1 AHRS姿态解算结构框图

1.1 AHRS动力学模型

描述AHRS动力学模型的方法有欧拉角法、方向余弦法、四元数法等。本文中,使用四元数微分方程表示AHRS动态模型[11]如下

(1)

即

利用四元数微分方程的比卡求解法,使(1)式离散化可得

(2)

式中

1.2 加速度计观测模型

图2为重力加速度在全局坐标系G与载体坐标系B中的示意图,且规定重力加速度矢量为单位矢量,即

‖g‖=‖a‖=1

式中：g为在全局坐标系G中测量的重力加速度；a为在载体坐标系B中测量的重力加速度。

图2 重力加速度示意图

如果把单位矢量g与a看作零标量的四元数,则g与a间的变换关系可用四元数乘法表示为

g=q(tk)⊗a⊗q*(tk)

(3)

经过变换可得

M′(a)q(tk)-M(g)q(tk)=0

(4)

式中,M(g)与M′(a)表示由零标量的四元数g与a构成的矩阵,参见文献[11]。

2 自适应扩展卡尔曼滤波器设计

本文所提出的自适应扩展卡尔曼滤波算法的数学描述如(5)式、(6)式所示,其算法流程框图如图3所示。

图3 自适应扩展卡尔曼滤波算法流程框图

状态方程为

Xk=Φk/k-1αXk-1+Wk-1

(5)

量测方程为

Zk=HkXk+Vk

(6)

式中：Φk/k-1为tk-1～tk时刻的一步转移矩阵;Hk表示量测矩阵;Vk和Wk分别表示激励噪声、量测噪声。

要求Wk和Vk满足[12]:

(7)

式中：Qk表示系统噪声方差矩阵；Rk表示量测噪声方差矩阵。

2.1 状态转移矩阵与量测矩阵

选取姿态四元数为状态变量,则由(2)式可知,系统状态方程的状态转移矩阵为

(8)

在(4)式中,令矩阵

(9)

向量

Zk=0

(10)

则(4)式可改写为

Zk=Hkq(tk)

(11)

比较(6)式与(11)式,则系统量测矩阵为(9)式所示。

2.2 系统噪声协方差矩阵

当MEMS 陀螺仪不存在噪声、零漂等因素的影响时,离散四元数微分方程为

(12)

或者

(13)

式中,ω°表示理想状态下,陀螺仪输出的角速率。

由于陀螺仪在微小时间间隔Δt内,其真实的角增量Δθ°无法测量。因此假设在第k个时间间隔内,陀螺仪的实际输出与真实角增量的误差为δθk,则有

Δθk/k-1=Δθ°k/k-1+δθk/k-1

(14)

相应的,实际状态转移矩阵与真实状态转移矩阵的误差为ΔΦk/k-1,即有

(15)

把(15)式代入(13)式可得

(16)

由文献[4]可知

δΘk/k-1q(tk-1)=Ξ(q(tk-1))δθk/k-1

(17)

式中

设陀螺仪的输出噪声为ngyro,则有

(18)

则系统噪声协方差矩阵为

(19)

式中,Σgyro为陀螺仪噪声协方差矩阵。

2.3 量测噪声协方差矩阵

量测噪声主要由加速度计产生。设加速度计的输出噪声为nacc,则有

nacc=a-a°

(20)

式中,a°表示载体坐标系下加速度计的真实值。

实际量测矩阵与理想量测矩阵误差为

(21)

把(21)式代入(11)式可得

0=Hkq(tk)-ΔHkq(tk)

(22)

类似(17)式,-ΔHkq(tk)变形为

(23)

则量测噪声协方差矩阵为

(24)

式中，Σacc为加速度计噪声协方差矩阵。

(24)式得到的量测噪声协方差矩阵Rk在应用过程中很有可能是奇异的,为了避免矩阵的奇异,需要对该量测噪声协方差矩阵Rk进行改进[5],即

(25)

2.4 自适应矩阵因子

(26)

式中,矢量l表示在包含航向误差的四元数坐标变换下的地磁场矢量。假设真实的先验地磁场矢量为

(27)

则有

(28)

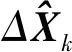
(29)

把(29)式代入(28)式可得

(30)

(31)

由此可知,自适应矩阵为

(32)

3 实验验证分析

3.1 ARHS传感器

本文使用AH-100B AHRS传感器对上述自适应扩展卡尔曼滤波算法进行了有效性验证。该AH-100B传感器集成了三轴陀螺、三轴加速度、三轴磁场计,输出数据分别为ω,a和m。传感器及特性参数分别如图4和表1所示。

表1 AH-100B AHRS传感器特性参数

图4 AH-100B AHRS传感器

3.2 静态姿态测试

自适应扩展卡尔曼滤波算法的初始状态由文献[1]中的算法给出,均方误差初始矩阵为单位矩阵。在算法中,假设三轴陀螺仪输出数据的方差相等,且

(33)

三轴加速度计输出数据的方差相等,且

(34)

参数β选取为0.03。

完成参数设置后,在ROS平台下进行了实验,并使用rqt-plot软件绘制出载体姿态四元数输出波形,如图5所示。

图5 姿态四元数输出波形

在图5中,姿态四元数的分量w在0.993～0.994之间变化,分量x在-0.004～-0.002之间波动,分量y在0.005～0.007之间波动,分量z在-0.114～-0.110之间波动。

通过上述分析可知,虽然姿态四元数的分量z所包含的噪声比其他3个分量大,但是基本保持在同一水平线上,因此有效消除了陀螺仪姿态解算过程中的累积误差。

3.3 动态姿态测试

为了验证该自适应扩展卡尔曼滤波算法在系统运动过程中的有效性,分别向搭载AH-100B航姿参考系统的ROS机器人平台输入三轴正交的抖动脉冲,如图6所示。

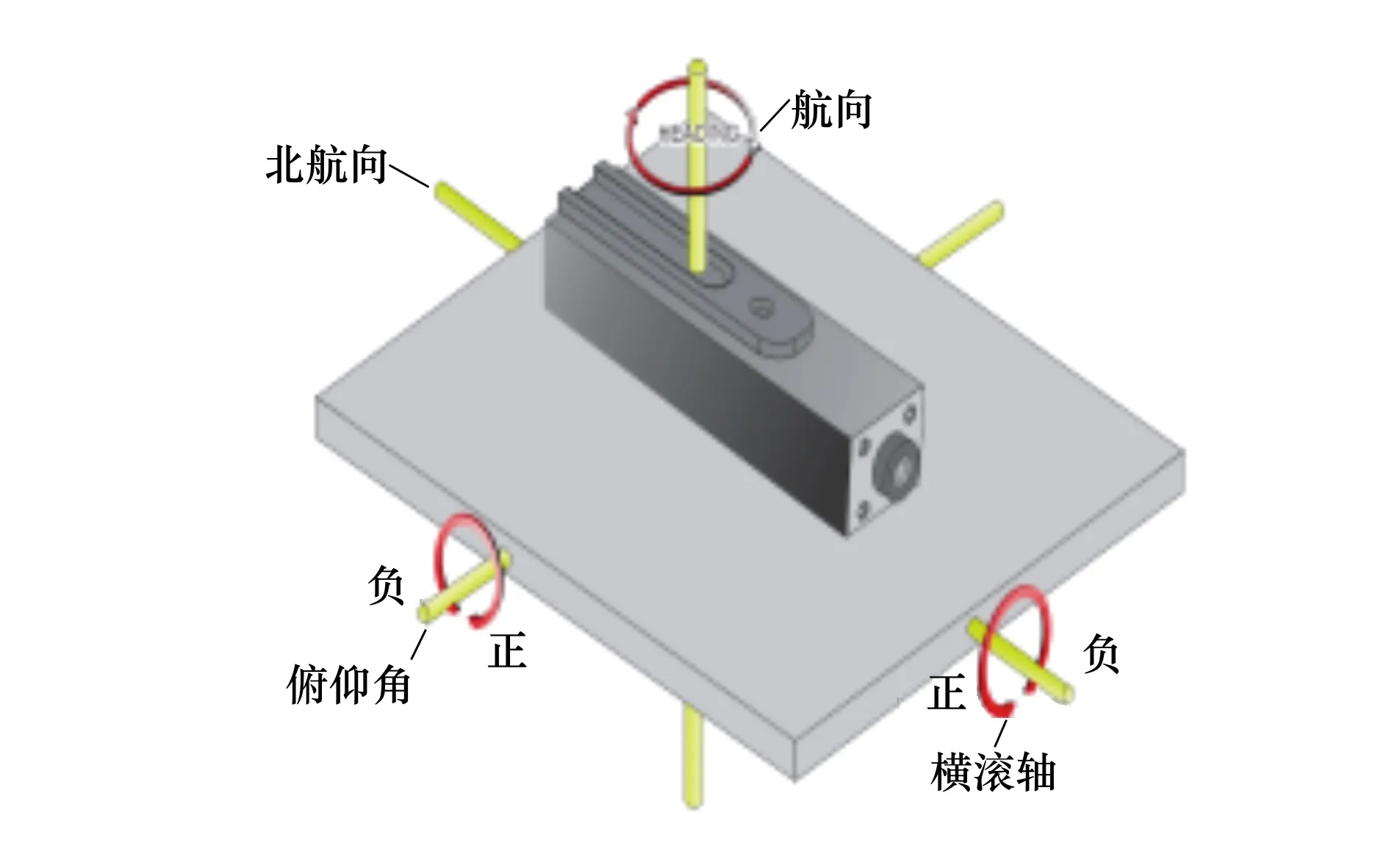
图6 AHRS中输入抖动脉冲

图7为分别向俯仰轴、横滚轴及偏航向轴输入正负抖动脉冲,载体姿态欧拉角的变化曲线。该图中,当系统输入正抖动脉冲时,载体横滚角、俯仰角及航向角都可以收敛到输入抖动脉冲之前的姿态;当系统输入负抖动脉冲时,3个姿态角同样可以收敛到输入抖动脉冲之前的姿态。因此该自适应扩展卡尔曼滤波算法具有良好的动态性能。

3.4 不同算法性能比较

本文对上述文献中提出的算法与自适应扩展卡尔曼滤波算法进行了比较,如图8所示。

图8a)、b)中,自适应扩展卡尔曼滤波算法、互补滤波算法与扩展卡尔曼滤波算法的俯仰角及横滚角输出波形图变化幅度较小,且比较平直。由于自适应扩展卡尔曼滤波与扩展卡尔曼滤波都是通过重力加速度信息对系统俯仰角及横滚角进行修正,因此两者的俯仰角及横滚角变化曲线重合。相较于基于四元数的互补滤波算法,自适应扩展卡尔曼滤波算法与扩展卡尔曼滤波算法中包含的噪声较小。

图8c)中,互补滤波器的航向角变化曲线在5°～10°范围内变化,精度大约为4°。扩展卡尔曼滤波算法的航向角变化曲线随着时间的增加逐渐偏离初始航向角,具有较大的累积误差。相较于上述2种算法,自适应扩展卡尔曼滤波算法的航向角变化约为0.5°。综上所述,自适应卡尔曼滤波算法有效解决了载体姿态的累积误差较大的问题,同时提高了姿态解算精度。

图7 输入抖动脉冲的姿态欧拉角变化曲线

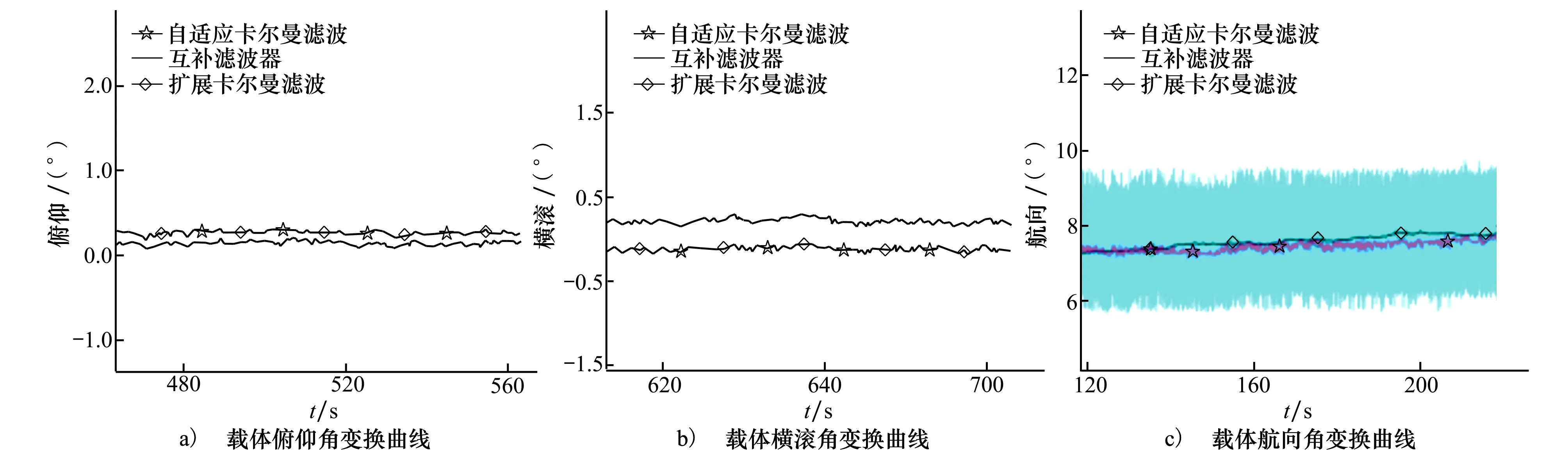
图8 不同算法姿态欧拉角输出波形

4 结 论

针对AHRS传感器中的MEMS陀螺仪在姿态解算过程中,输出姿态存在噪声较大及累积误差等问题,本文提出了一种自适应卡尔曼滤波算法。该算法融合了地球物理场(重力场,地磁场)信息,不但能够消除陀螺仪在姿态解算过程中的累积误差,也可以保证解算姿态的精度。并在ROS机器人平台上进行了验证,试验结果表明了该算法的有效性。