考虑趋肤效应和动态磁滞效应的电机旋转铁芯损耗模型

宋 泽，李永建※，张长庚，刘 洋



考虑趋肤效应和动态磁滞效应的电机旋转铁芯损耗模型

宋 泽1，李永建1※，张长庚1，刘 洋2

（1. 河北工业大学电气工程学院省部共建电工装备可靠性与智能化国家重点实验室，天津 300130；2. 全球能源互联网研究院有限公司，北京 102211）

实际农业用电设备铁芯损耗的预测不准是趋肤效应造成农用电器效率低下、使用成本升高的重要原因之一。针对这一问题，该文综合考虑了交变激励下趋肤效应、局部磁滞作用和动态磁滞回环对经典铁芯损耗模型系数的影响，将系数修正后的交变模型引入旋转铁芯损耗模型中，提出一种基于正交分解和损耗分离的改进无取向硅钢叠片旋转铁芯损耗模型。利用磁特性测量装置进行不同频率下的铁芯损耗测量，对所建模型验证。结果表明：与经典铁芯损耗模型和只考虑单一因素的改进模型相比，该模型在高频和高磁密下的铁芯损耗计算精度分别提高了25.32%和9.16%。研究结果可为农用电气设备的电机设计与优化提供参考。

模型；试验；磁损耗；趋肤效应；磁滞回环

0 引 言

如何通过提高电机的效率减少资源浪费是许多农用电机应用中亟待解决的问题。一方面可以采用新材料、提出新结构、优化旧有结构[1]；另一方面可以通过改进电机的控制方式及控制策略[2-3]使其运行在最佳效率范围内。而上述2种途径均基于对电机铁芯损耗的精确估算[4-6]。

实际电机使用情况下的定子铁芯处于旋转磁场中，产生的旋转损耗不同于单一方向交变激励产生的损耗[7-10]。而硅钢叠片生产厂家由于设备和规范问题往往只测量了叠片在单一激励方向下的铁芯损耗曲线，这对于电机定子的设计和控制策略的精确性产生了较大影响。关于电机铁芯损耗的估算，19世纪S Steinmetz提出了铁芯磁滞损耗公式[11]，该公式适用于激励为正弦工频的情况，20 世纪90年代Bertotti G在其基础上增加了额外损耗[12]，随着电力电子器件的出现和其应用技术的迅速发展，此类公式产生了多种变形。Aldo Boglietti提出了一种任意电压波形均可适用的软磁材料的铁芯损耗计算方法[13]，该方法基于工程应用的数据拟合，能够较快的计算出损耗值大小。随后，Aldo Boglietti在对大量数据分析的基础上提出了一种适于脉冲宽度调制（pulse width modulation，PWM）供电的异步电机铁耗模型[14]，具有良好的可重复性。以上方法均是从磁路的角度出发研究损耗，需要进行解析，准确度不高。

目前主流的铁芯损耗计算方法都是基于对已知测量数据进行参数识别之后采用数据拟合得出系数[15-16]，因此计算铁芯损耗方法的准确性基于精确的铁芯损耗测量。对于磁性材料的交流特性测试方法目前分为一、二、三维磁特性测量。一维方法比较成熟[17]、二维测量装置国际上目前并没有统一的标准，根据励磁方式和被测样品形状的不同分为水平方形样片旋转测量装置[18]、水平圆型样片旋转测量装置[19]、垂直型旋转测量装置[20-21]等，而考虑到实际中农用电气设备处于的磁场为三维磁场，一、二维测量装置无法真实模拟实际磁场。随着电子计算机技术的发展，有限元软件的出现使得材料层面的模型可以直接应用于实际设备中。Zhu等[22]考虑了交变激励下动态磁滞回环的情况，用变系数的方法进行改进。黄平林则在考虑磁滞回线面积和磁密关系的基础上引入修正系数来表示局部磁滞回环对磁滞损耗的影响[23]。上述两者虽然都包含了谐波产生的影响但并没有考虑到实际电气设备处于旋转磁场的情况。江善林等[24]将交变激励下趋肤效应对磁滞损耗的影响引入旋转模型中，提出了在旋转磁通条件下考虑趋肤效应的改进铁芯损耗公式，但并没有考虑谐波对旋转磁化下磁滞损耗的影响。

本文考虑到电机铁芯实际处于的局部磁场为旋转磁场，在原有只考虑单一因素影响的交变激励铁芯损耗公式基础上进行综合考虑，并将其引入旋铁芯损耗模型，对损耗系数进行修正。将合成的旋转场进行分解，对2个方向的计算值进行耦合，得到旋转磁化条件下的铁芯损耗公式。在此基础上运用磁特性测量装置对样品进行测量，将测量值进行数据拟合得出本文改进模型的计算值，并将改进模型计算值和测量值以及只考虑单一因素的铁芯损耗公式计算值进行比对，以期验证模型精度，为农用电机的设计和优化提供更为直接的理论参考。

1 铁芯损耗的损耗分离

1.1 交变激励下的铁芯损耗

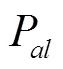
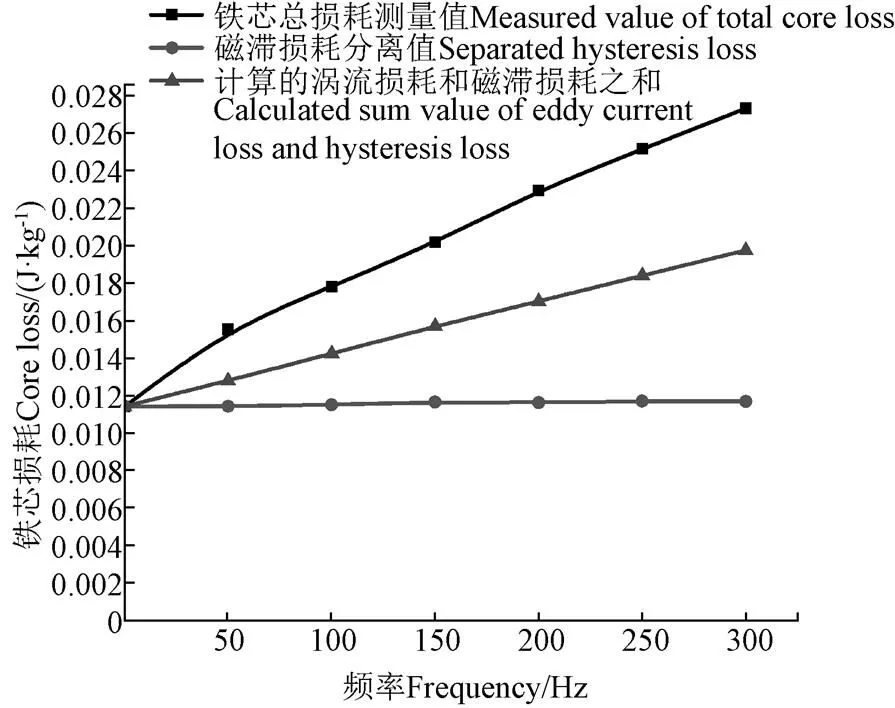
图1 硅钢片B35A210在磁密0.5 T时的铁芯损耗分离结果

1.2 旋转磁场下的铁芯损耗

一维交变场的磁密图像呈一条直线，实际空间磁场磁密必然是三维的，而由一维向三维过渡过程中，二维旋转场是必不可少的。旋转场的磁密矢量大小和方向随时间变化，其顶点形成的轨迹为椭圆或圆形。旋转磁场的形成必须使外加磁场的方向能与被测样片的轧制方向成任意角度，其实现方法是产生2路相互垂直并且相差一定相位角的磁场，被测硅钢样片的磁密矢量值在2个相互垂直磁路的平面上会合成一个确定的图形，当图形为椭圆时，说明磁场既有旋转分量，又有交变分量。根据坡印廷矢量定理[26]计算出旋转磁场下磁性材料每周期的能量损失[27]，进而得到旋转磁场下的总损耗P为：

2 旋转磁化下铁芯损耗模型的建立

2.1 磁滞损耗模型修正

注：和为铁芯材料在2个相互垂直激励磁路方向测得的磁密，T；，为椭圆形磁密轨迹的长轴长和短轴长，T；为旋转磁密的幅值，数值上为和矢量和的模值，大小同，T；θ为椭圆轨迹长轴与被测铁芯材料轧制方向的夹角，rad。

Zhu[8]给出磁性材料在旋转磁化中全部的磁滞损耗为：

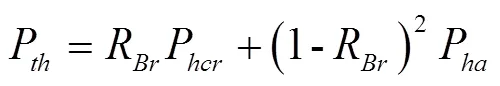
电能变换设备的大规模应用带来的大量谐波会产生局部磁滞回环，影响经典公式中磁滞损耗部分的计算准确性。考虑到磁滞回线面积与磁密的关系，磁滞损耗中引入表示局部磁滞回环中磁密变化与整体最大磁密的比值的修正系数[30]：

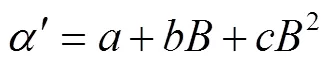
式中为铁芯材料的磁密，T；、、为随激磁频率变化而变化的常系数，通过取对数拟合求出[32]。

2.2 总损耗模型的确定

当铁芯材料置于变化磁场中时，磁畴壁会发生跳跃的、不连续的巴克豪森跃变与弯曲运动，从而在其内部产生环绕畴壁边界的磁通，产生感应电压或电流，进而引起铁芯材料的欧姆损耗，即交变模型中的额外总损耗。在交变模型基础上，考虑旋转场中磁密运动轨迹并对其进行正交分解，得出涡流总损耗和额外总损耗分别如下所示：

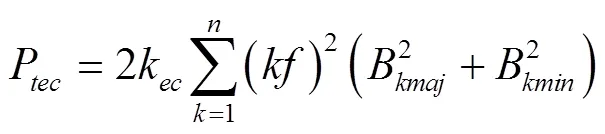
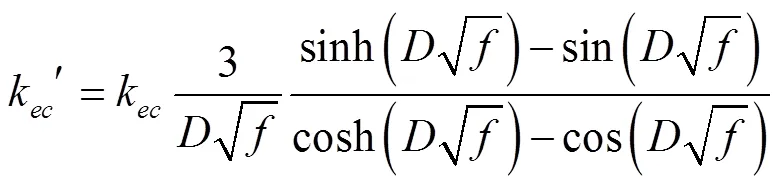
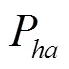
3 验证试验

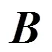
如果只考虑铁芯材料处于低频磁场的情况则测量条件和现实工况差距较大，为了进一步模拟现实中电气设备的运行状况，试验的激磁频率选择50、100、200 Hz。图4显示了50、100、200 Hz下本文模型的计算值和测量值的比较，误差平均值分别为0.123 1、0.147 5、0.192 W/kg，分别占测量值的11.55 %、8.03 %和6.56 %。其中绝对误差随频率增大而增大主要是由于铁芯总损耗随着频率的增加而增加，相对误差的逐渐减小说明本文提出的模型计算值精度在高频率下更加精确。

图5为不同频率下35WW270硅钢片铁芯损耗计算值和测量值的对比。图5a、5b为50和200 Hz下本文模型、经典铁芯损耗模型、考虑单一因素的改进模型的计算值和测量值的比较。图5c为200 Hz时样品在激磁方向为材料的切向、轧制方向时的交变铁芯损耗和旋转磁化下铁芯损耗的对比。从图5a、5b中可以看出，经典铁芯损耗公式在频率较高时的计算误差相比本文提出的改进模型更大，50 Hz时本文模型铁芯损耗的计算值与测量值的误差比经典铁芯损耗模型减小9.21%，而200 Hz时则减小39.76%。由图5b可知，在低磁密时只考虑单一因素的改进模型与本文模型在精度方面差距不明显，当磁密较高时本文模型的精确度更高：在磁密为0.95 T时对比只考虑趋肤效应、局部磁滞作用、动态磁滞回环的铁芯损耗模型，本文模型的计算精度分别精确提高4.34%、15.2%、7.95%。而在磁密为0.38 T时分别提高1.94%、3.88%、7.37%。

1.三维磁特性测量装置 2.电阻 3.电容箱 4.采集卡 5.示波器 6.功率分析仪 7.功率放大器 8.信号放大电路 9.电流表 10.Labview界面1.3D magnetic properties measurement device 2.Resistance 3.Capacitance box 4.Acquisition card 5.Oscilloscope 6.Power analyzer 7.Power amplifier 8.Signal amplification circuit 9.Ammeter 10.Labview interfacea. 三维磁特性测量系统各部分设备a. Equipment component of 3D magnetic properties measurement system1.励磁线圈 2.铁轭 3.内置被测铁芯材料的传感箱 4.匀场保护层1.Excitation coil 2.Iron yoke 3.Sensing box with built-in core material for test 4.Protective layer for uniforming magnetic fieldb. 磁特性测量装置主磁路和被测立方体样品b. Magnetic circuit of magnetic properties measurement device and tested cube sample 1.传感线圈 2.传感线圈 3.传感线圈 4.传感线圈 5.传感线圈 6.传感线圈1.sensing coil 2.sensing coil 3.sensing coil 4.sensing coil 5.sensing coil 6.sensing coilc. 传感箱结构c. Structure of sensing box

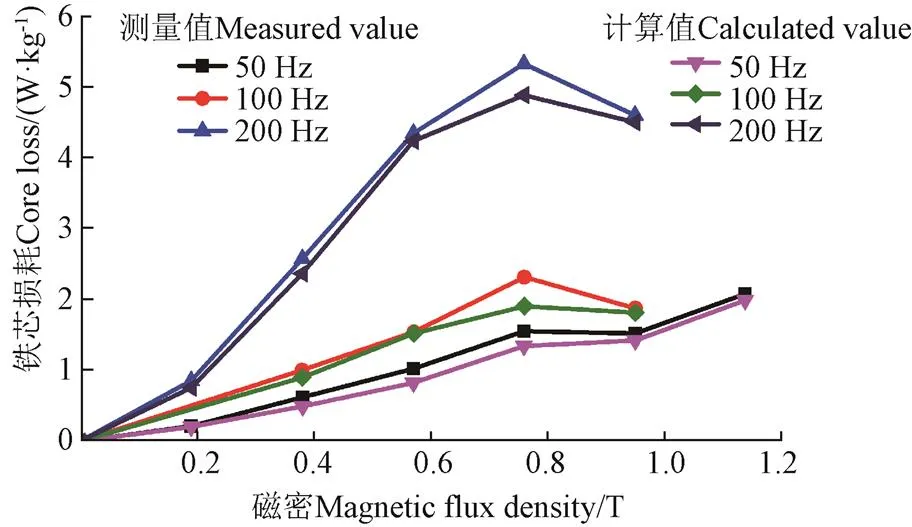
图4 硅钢片35WW270铁芯损耗测量值和计算值对比

图5c中交变激励下的铁芯损耗大于旋转磁化的铁芯损耗，这是由于在交变激励中，铁芯处于不停换向的磁场中，铁芯材料中磁畴的不可逆换向和畴壁移动一直发生，致使磁滞损耗一直随磁密增加而增加；而在旋转磁场磁化作用下，由于外磁场为方向固定的矢量，磁密接近饱和（0.76T）后由于材料内部磁化强度逐渐和外界磁场强度一致，畴壁逐渐消失，而由畴壁可逆和不可逆运动带来的磁滞损耗和额外损耗也逐渐减小至0，总损耗主要表现为经典涡流损耗。图4中50 Hz时旋转铁芯损耗的下降趋势不如200 Hz时的明显，主要是由于材料在低频时磁化激励的周期较长，磁滞损耗减少速度比200 Hz时的慢。在磁密逐渐饱和的过程中50 Hz激励下的铁芯总损耗中磁滞损耗的占比比200 Hz激励下的高。以磁密为0.8 T时为例，50 Hz时的铁芯总损耗比200 Hz时高了33.54%。而200 Hz时，在磁密由0.2 T增大到0.9 T过程中，磁滞损耗在铁芯总损耗占比减少了12.33%，铁芯总损耗中的磁滞损耗部分随之减少，只剩经典涡流损耗。由于高频时的涡流损耗远高于低频，所以对外呈现的铁芯总损耗数值更大。

图5 硅钢片35WW270铁芯损耗测量值和计算值对比 Fig.5 Core loss comparison of silicon steel sheet 35WW270 between measured value and calculated value

4 结 论

本文根据农用电器的实际使用情况，综合考虑趋肤效应、局部磁滞作用和动态磁滞回环，构建了适用于无取向硅钢片材料的旋转铁芯损耗模型，并以农用电气设备中常用的无取向硅钢片35WW270为对象进行试验验证。得到如下结论：

1）与经典铁芯损耗模型相比，本文提出的改进模型考虑了实际应用中存在旋转磁化的条件，综合了高频谐波的趋肤效应、局部磁滞作用和动态磁滞回环的情况，计算精度较高，误差不超过11.55%。与经典铁芯损耗模型和只考虑单一因素的改进模型相比，本文模型在高频和高磁密下的铁芯损耗计算精度分别提高了25.32%和9.16%。而且本文改进模型随激磁频率的增加而更接近于测量值。当激磁频率为50 Hz时本文模型对比经典铁芯损耗模型的误差减小9.21 %，而200 Hz时误差则减小39.76 %。

2）无取向硅钢片的磁密尚未饱和时，交变激励下的铁芯损耗随磁密增加而增加，而旋转磁化条件下的铁芯损耗则随磁密增加到一定值后开始减少。本文旋转磁化下的铁芯损耗在磁密增加到0.76 T处开始出现减少，而交变激励下的铁芯损耗则一直随磁密增加而增加。

3）交变激励情况下和旋转磁化时铁芯损耗随磁密增加的不同变化趋势主要是由两者磁滞损耗的不同变化趋势造成的。而磁滞损耗的不同变化趋势是由铁芯材料中磁畴壁运动的不同方式所导致的。

[1] 葛研军，袁直，贾峰，等. 笼型异步磁力耦合器机械特性与试验[J]. 农业工程学报，2016，32(12)：68－74. Ge Yanjun, Yuan Zhi, Jia Feng, et al. Mechanical properties an testing for squirrel cage asynchronous magnetic coupler[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(12): 68－74. (in Chinese with English abstract)

[2] 杨泽斌，李方利，陈正，等. 基于低频信号注入法的无轴承异步电机转速自检测控制[J]. 农业工程学报，2017，33(2)：41－47.Yang Zebin, Li Fangli, Chen Zheng, et, al. Revolving speed self-detecting control base on low-frequency signal injection for bearingless induction motor[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(2): 41－47. (in Chinese with English abstract)

[3] 孙宇新，沈启康，叶海涵，等. 基于改进UKF的无轴承异步电机无速度传感器控制[J]. 农业工程学报，2018，34(19)：74－81. Sun Yuxin, Shen Qikang, Ye Haihan, et, al. Speed-sensorless control system of bearingless induction motor based on modified adaptive fading unscented kalman filter[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(19): 74－81. (in Chinese with English abstract)

[4] Daisuke Yokoyama, Takeru Sato, Takashi Todaka, et al. Comparison of iron loss characteristics of divided cores considering vector magneticproperties[J].IEEE Transactions on Magnetics, 2014, 50(4): 1－4.

[5] Ding Xiaofeng, Ren Suping, Xiong Yanwen, et al. 2-D magnetic properties measurement system for electrical steel sheets considering laminated direction mechanical stress[J]. IEEE Transactions on Magnetics, 2017, 53(10): 1－11.

[6] Xu Weijie, Duan Nana, Wang Shuhong, et al. Modeling of magnetic properties in soft magnetic composite material under rotational magnetization[J]. IEEE Transactions on Industrial Electronics, 2017, 64(3): 2459－2467.

[7] Natheer Alatawneh, Pragsen Pillay. The minor hysteresis loop under rotating magnetic fields in machine laminations[J]. IEEE Transactions on Industry Applications, 2014, 50(4): 2544－2553.

[8] Zhu Jianguo, Victor Stuart Ramsden. Improved formulations for rotational core losses in rotating electrical machines[J]. IEEE Transactions on Magnetics, 1998, 34(4): 2234－2242 .

[9] Ashraf Rohanim Asari, Guo Youguang, Zhu Jianguo. Core loss measurement under elliptical loci of magnetic flux density[C]// 2017 20th International Conference on Electrical Machines and Systems (ICEMS). Sydney, NSW: IEEE, 2017: 1－4.

[10] 杨娜，李丹丹，宋寅卯. 软磁复合材料损耗特性的研究进展[J]. 电工材料，2018(4)：32－35. Yang Na, Li Dandan, Song Yingmao. Review of loss characteristics of soft magnetic composites material[J]. Electrical Engineering Materials, 2018(4): 32－35. (in Chinese with English abstract)

[11] Chas Proteus Steinmetz. On the law of hysteresis[C]// Transactions of the American Institute of Electrical Engineers, New York: IEEE, 1892, 4(1): 3－29.

[12] Aldo Boglietti, Paolo Ferraris, Mario Lazzari, et al. About the possibility of defining a standard method for iron loss measurement in soft magnetic materials with inverter supply[J]. IEEE Transactions on Industry Applications, 1997, 33(5): 1283－1288.

[13] Aldo Boglietti, Andrea Cavagnino, Mario Lazzari, et al. Predicting iron losses in soft magnetic materials with arbitrary voltage supply: an engineering approach[J]. IEEE Transactions on Magnetics, 2003, 39(2): 981－989.

[14] Aldo Boglietti, Andrea Cavagnino, Dan M Ionel, et al. A general model to predict the iron losses in PWM inverter-fed induction motor[J]. IEEE Transactions on Industry Applications, 2010, 46(5): 1882－1890.

[15] 迟青光，张艳丽，曹政，等. 电工钢片旋转损耗特性分析与损耗模型修正[J]. 中国电机工程学报，2017，37(8)：2418－2426. Chi Qingguang, Zhang Yanli, Cao Zheng, et al. Analysis of rotational loss property in an electrical steel sheet and correction of loss model[J]. Proceedings of the CSEE, 2017, 37(8): 2418－2425. (in Chinese with English abstract)

[16] 龚文君，黄邵刚，杨玉文，等. ANSYS Maxwell硅钢片铁耗系数提取方法的实现[J]. 电机与控制应用，2016，43(4)：82－85. Gong Wenjun, Huang Shaogaug, Yang Yuweu, et al. Realization of the method of extracting iron loss coefficient of silicon steel sheet in ANSYS Maxwell[J]. Electric machines & control application, 2016, 43(4): 82－85. (in Chinese with English abstract)

[17] 李玉梅. 考虑电工钢片旋转磁特性的感应电机铁心损耗问题研究[D].沈阳：沈阳工业大学，2013. Li Yumei. Study on Iron Core Loss of the Induction Motor Considering Rotating Magnetic Property of the Electrical Steel Sheets[D]. Shenyang: Shenyang University of Technology, 2013. (in Chinese with English abstract)

[18] Martin A Rückert, Patrick Vogel, Anna Vilter, et al. Rotational drift spectroscopy for magnetic particle ensembles[J]. IEEE Transactions on Magnetics, 2015, 52(2): 1－4.

[19] Jemimah C Akiror, John Wanjiku, Pragasen Pillay, et al. Rotational core loss magnetizer: design and measurements[J]. IEEE Transactions on Industry Applications, 2018, 54(5): 4355－4364.

[20] Anouar Belahcen, Paavo Rasilo and Antero Arkkio. Segregation of iron losses from rotational field measurements and application to electrical machine[J].IEEE Transactions on Magnetics, 2014, 50(2): 893－896.

[21] 曹政. 基于二维磁特性测量技术的电工钢片损耗特性研究[D]. 沈阳：沈阳工业大学，2016. Cao Zheng. Research on Power Loss Properties of Electrical Steel Sheet Based on Measurement Technology of Two-Dimensional Magnetic Properties[D]. Shenyang: Shenyang University of Technology, 2016. (in Chinese with English abstract)

[22] Zhu Lixun, Junho Park, Koh Chang-seop. Adynamic hysteresis model based on vector-play model for iron loss calculation taking the rotating magnetic fields into account[J]. IEEE Transactions on Magnetics, 2018, 54(3): 1－4.

[23] 黄平林. 旋转电机铁心损耗的分析与计算[D]. 南京：东南大学，2007. Huang Pinglin. Analysis and Calculation of Rotating Core Loss[D]. Nanjing: Southeast University, 2007. (in Chinese with English abstract)

[24] 江善林，邹继斌，徐永向，等. 考虑旋转磁通和趋肤效应的变系数铁耗计算模型[J]. 中国电机工程学报，2011，31(03)：104－110. Jiang Shanlin, Zou Jibin, Xu Yongxiang, et al. Variable coefficient iron loss calculating model considering rotational flux and skin Effect[J]. Proceedings of the CSEE, 2011, 31(3): 104－110. (in Chinese with English abstract)

[25] 李劲松，杨庆新，李永建，等. 考虑谐波及集肤效应的电工钢片旋转异常损耗计算与测量[J]. 电机与控制学报，2016，20(6)：42－49. Li Jingsong, Yang Qingxin, Li Yongjian, et al. Measurement and calculation of rotating anomalous loss in electrical steel sheets considering harmonics and skin effect[J]. Electric Machines and Control, 2016, 20(6): 42－49. (in Chinese with English Abstract)

[26] 曹磊. 硅钢叠片材料的损耗特性测及工程模拟研究[D]. 天津：河北工业大学，2016.Cao Lei. Core Loss Characteristics Measurement and Engineering Modeling of the Silicon Steel Lamination[D]. Tianjin: Hebei University of Technology, 2016. (in Chinese with English abstract)

[27] Wan Xuezhi, Li Yongjian, Li Jingsong, et al.Orthogonal decomposition of core loss along rolling and transverse directions of non-grain oriented silicon steels[J]. AIP Advances, 2017, 7(5): 1－7.

[28] Zhu Jianguo. Numerical Modelling of Magnetic Materials for Computer Aided Design of Electromagnetic Devices[D]. Sydney: University of Technology Sydney, 1994.

[29] 李永建，王利祥，张长庚，等. 基于三维励磁结构的电工磁材料动态磁特性测试与分析[J]. 电工技术学报，2018，33(1)：166－174.Li Yongjian, Wang Lixiang, Zhang Changgeng, et al. Dynamic magnetic properties testing and analysis of the electric magnetic materials based on three-dimensional excitation structure[J]. Transactions of China Electrotechnical Society, 2018, 33(1): 166－174. (in Chinese with English abstract)

[30] 曹诗侯. 铁磁材料非正弦激励下的损耗计算方法研究[D]. 杭州：浙江大学，2017. Cao shihou. Predicting Iron Losses in Magnetic Materials with Non-Sinusolidal Power Supply[D]. Hangzhou: Zhejiang University, 2017. (in Chinese with English abstract)

[31] K Atallah, Z Q Zhu, D Howe. An improved method for predicting iron losses in brushless permanent magnet DC drives[J]. IEEE Transactions on Magnetics, 1992, 28(5): 2997－2999.

[32] Chen Yicheng, Pragasen Pillay. An improved formula for lamination core loss calculations in machines operating with high frequency and high flux density excitation[C]// Conference record of the 2002 IEEE Industry Applications Conference. 37th IAS Annual Meeting(Cat. No.02CH37344). Pittsburgh, PA, USA: IEEE, 2002: 759－766.

[33] Mehdi Taghizadeh Kakhki, Jérôme Cros, Philippe. Viarouge. New approach for accurate prediction of eddy current losses in laminated material in the presence of skin effect with 2-D FEA[J]. IEEE Transactions on Magnetics, 2016, 52(3): 1－4.

Rotating core loss model for motor considering skin effect and dynamic hysteresis effect

Song Ze1, Li Yongjian1※, Zhang Changgeng1, Liu Yang2

(1.300130,; 2.102211)

In order to improve the efficiency of agricultural electrical equipment and reduce energy consumption, many scholars attempt to estimate the iron loss accurately. The analysis of finite element showed that in rotational electric machines total core loss comprised alternating core loss and rotational core loss. Precise measured value and modeling of rotational core loss in electrical steel sheets and rotating electrical machines is very important to design and optimize the kind of agricultural motor. According to the separated core loss model under alternative excitation, the core loss can be separated into hysteresis loss, eddy current loss and excess loss. As for alternating core loss, the specific core loss with a circular magnetic flux density can also be separated into 3 portions: the rotational hysteresis loss, the rotational classical eddy-current loss and the rotational excess loss. By means of fourier analysis, the rotating core loss model which considered the influence of alternating and rotating magnetic field, skin effect, dynamic hysteresis loop and minor hysteresis loop was proposed in this paper. Actually, the static hysteresis loop and the dynamic hysteresis loop are different, when the flux density is in saturation, the hysteresis loop shape will be changed. In order to consider the complex behavior of dynamic hysteresis, variable coefficient hysteresis loss was used in the model. The classic exponential coefficient were chosen to be substituted in to the 3 parameters polynomial and fitted out the rotational hysteresis loss with the logarithm. Considering the impact of skin effect at high frequencies, eddy-current loss coefficient were corrected in the paper. Minor hysteresis loop generated by the massive harmonic components leaded the inaccurate prediction of the core loss, the influence of minor hysteresis loop was described by the modified coefficient in the improved formulations, and the modified coefficient was related to the ratio of local flux density to flux density amplitude. By applying orthogonal decomposition technology, 2 mutually orthogonal magnetic flux field was used to describe elliptical rotating magnetic field and replace the rotating loss data. Taking an object affected by the elliptical flux density as an example, the applied magnetic field intensity might not be an elliptical vector because of the nonlinear magnetic flux density-magnetic field intensity relationship and magnetic anisotropy, when it was expanded into a fourier series, however, it shown that the higher harmonics of magnetic field intensity did not contribute to the total core loss as long as magnetic flux density only contains the basic components, the total core loss under the elliptical flux was the summation of alternating core loss and rotating core loss. In order to verify the accuracy of the improved model, a new 3D magnetic properties measurement system was used to measure the rotating core loss of electrical sheet steels. The 3D excitation structure consisted of 3 orthogonal C-shaped cores, 6 multilayer excitation coils which were wound around core poles, a sensing box with built-in core material was placed in the center of 3D magnetic properties measurement device, 6 thin pieces, named as protective layer of uniform magnetic field were fixed around the specimen to make the measured field more uniform at the surface of specimen. Experimental results showed that compared with the classical model and the improved model considering the single factor of skin effect or hysteresis loops only, the accuracy of core loss calculation value of the proposed model was increased by 25.32% and 9.16%, respectively, especially under the condition of high flux density and high frequency. When the frequency was 50 Hz, compared with the classical model, the accuracy of core loss calculation value of the proposed model was increased by 9.21%, and the accuracy was increased by 39.76% at 200 Hz. The comparison of measured value between alternating core loss and rotational core loss showed that the energy of magnetic domain could not accumulated to the maximum in a fixed direction that would lead to irreversible magnetic domain conversion under alternating excitation, which resulted in the increase of hysteresis loss with the increase of magnetic density.The research results can provide reference for the design and optimization of agricultural electrical equipment.

models; experiments; core loss; skin effect; hysteresis loop

2018-10-26

2018-12-29

国家重点研发计划（2017YFB0903904）；河北省百名优秀创新人才支持计划项目（SRLC2017031）

宋 泽，主要从事工程电磁场与磁技术。Email：837892770@qq.com

李永建，教授，博士，博士生导师，主要从事工程电磁场与磁技术。Email：liyongjian@hebut.edu.cn

10.11975/j.issn.1002-6819.2019.06.009

TM15

A

1002-6819(2019)-06-0074-07

宋 泽，李永建，张长庚，刘 洋. 考虑趋肤效应和动态磁滞效应的电机旋转铁芯损耗模型[J]. 农业工程学报，2019，35(6)：74－80. doi：10.11975/j.issn.1002-6819.2019.06.009 http://www.tcsae.org

Song Ze, Li Yongjian, Zhang Changgeng, Liu Yang. Rotating core loss model for motor considering skin effect and dynamic hysteresis effect[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(6): 74－80. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2019.06.009 http://www.tcsae.org